横向撞击力对铁路桥梁及行车影响的模型实验研究
2014-09-05崔堃鹏夏超逸杜宪亭
崔堃鹏,夏 禾,夏超逸,张 楠,杜宪亭
(北京交通大学 土木建筑工程学院,北京 100044)
我国高速铁路大量采用高架桥梁,跨线桥数量很大,桥墩被汽车撞击的可能性大大增加。桥梁受到汽车等撞击时,可能会引起支座与主梁的错位,使伸缩缝变形不协调,伸缩缝断裂,给桥梁结构埋下安全隐患,严重时会直接导致桥梁的塌落,后果极其严重[1-2]。尽管这些事故很少发生,但是它们一旦发生,将会对桥梁、铁路线、乘客带来灾难性的破坏和伤害。对于高速铁路桥梁,桥墩受到撞击时,即使桥梁结构不发生塌落,也将发生一定的振动和位移,从而影响桥上线路的平顺性和稳定性,引起桥上高速列车行车安全问题。
汽车与桥梁结构碰撞的作用机理复杂,涉及材料非线性、接触非线性以及动力效应问题,理论研究难度大,实验研究费用昂贵、破坏性大,至今鲜有公开发表的汽车撞击桥梁实验数据。英国Arup公司的汽车撞击桥墩和桥梁上部结构的足尺试验数据只是作为企业内部的研究报告,尚未公开[3]。美国密歇根大学El-Tawil等[4]采用非弹性的瞬态有限元模拟技术研究了汽车与桥墩之间的碰撞作用机理,给出撞击力时程和等效静力。北京交通大学夏超逸等[5-6]模拟汽车撞击力作用于桥墩和列车过桥全过程,结果分析表明汽车横向撞击使桥梁动力响应大幅增加,对高速列车运行安全有很大影响。
我国高速铁路设计规范[7]中规定:对遭受汽车撞击而无防撞措施的桥梁墩台,应检算汽车撞击状态,撞击力顺汽车行驶方向采用1 000 kN,垂直于汽车行驶方向采用500 kN,两个等效力不同时考虑,作用在路面以上1.2 m高度。欧洲Eurocode规范[8]中规定:对于汽车撞击力,考虑顺车向1 000 kN或者垂直于车向500 kN,作用在路面以上1.25 m高度。美国AASHTO规范[9]中规定:位于距道路边缘9 m以内或距铁路轨道中心线15 m的桥梁墩台,未安装防护装置时,设计时应考虑1 800 kN的车辆撞击力,该力在地面以上1.2 m位置从任意方向水平作用于结构。以上规范均未说明设计撞击力的来源及合理性,美国规范只是阐明规定源自于早期的足尺测试实验,也未考虑提及汽车撞击桥墩的动力相互作用。
在日益增多的铁路跨线桥被下行汽车撞击、列车运行速度越来越快和车次越来越密集、足尺试验难以实施的特定背景下,本文假定撞击在弹性范围内,定性非定量的尝试性地通过模型试验研究了横向撞击荷载作用下桥墩及桥上运行车辆的动力响应规律,以此研究横向撞击荷载作用下桥梁动力响应及桥上列车运行安全性。最后,根据撞击力时程探讨了瞬态撞击力的等效静力计算方法并进行了验证。
1 实验简介
试验在北京交通大学结构实验室的车-轨-桥耦合振动试验平台进行,平台及汽车模型见图1。在左侧桥墩旁设置了简易滑道,模型汽车沿滑道滑落撞击桥墩,撞击处布置力传感器(INV DFC-2型高弹性聚能力锤力传感器),采集撞击力时程。

图1 车-轨-桥实验平台和汽车模型
模型桥主梁长8 m,由4根10号工字钢焊接而成;每隔0.5 m设置竖向拉杆一共15根,拉杆直径1.4 cm;拱圈长度8.68 m,矢高1.35 m;桥墩采用圆形钢管,外径32.5 cm,壁厚0.6 cm,底端与地面固定;桥梁支座一端固定一端滑动;梁上铺设10 mm厚的聚乙烯整体道床板,在板上铺设钢轨,轨距为实际线路上轨道间距的十分之一,即143.5 mm。
桥梁各测点编号如图2所示:墩底布置应变测点片(测点A);墩顶布置横向加速度和位移测点(左墩C、D,右墩K、L),梁的1/4、1/2、3/4截面布置了横向加速度和动位移测点(E~J测点),分别布置加速度传感器和位移计测试,如图3所示。桥梁振动数据由东方所INV3020C型动态数据处理系统采集分析。
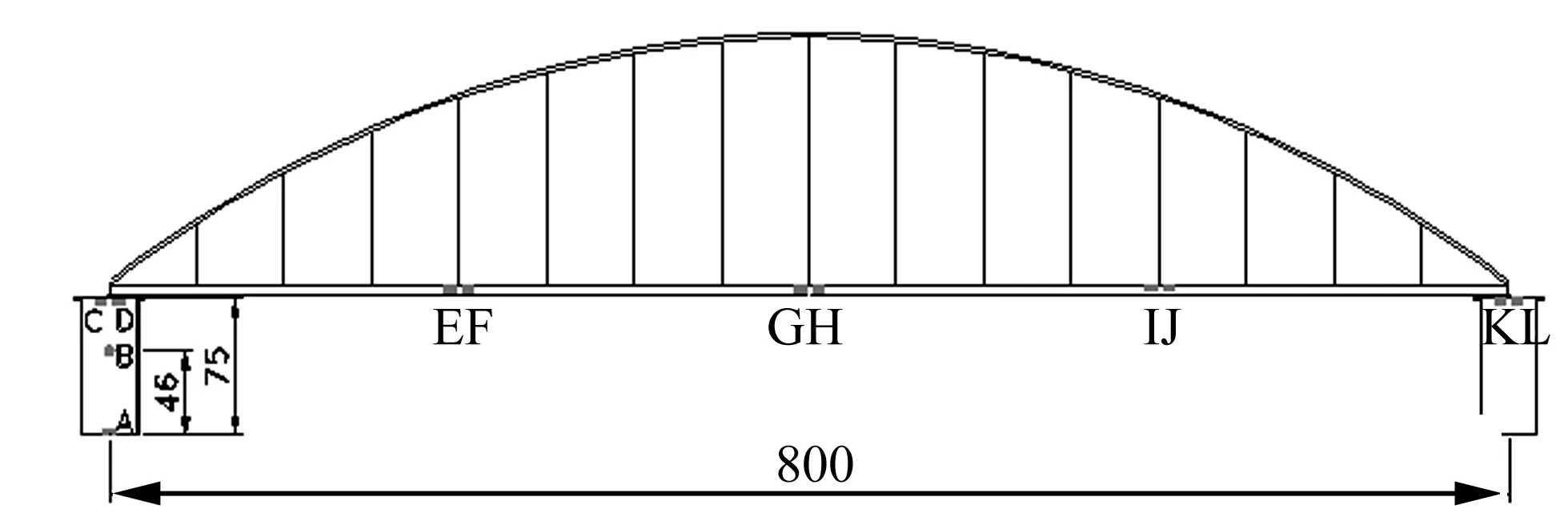
图2 模型梁各测点布置图(单位:cm)
车辆模型几何尺寸按照实际25 K型客车以1∶10的比例设计,模型总长2.55 m,前后转向架中心距1.8 m,两系悬挂装置。
采用无线传感器和信号采集分析系统测试车体的三向加速度时程,见图4。

图3 梁1/2截面加速度计和位移计

图4 无线传感器和信号采集分析系统
试验时,将车辆提升到不同高度释放,以获得不同的速度沿轨道通过桥梁,汽车以不同高度下落获得不同速度撞击桥墩,撞击时刻选择车辆一轮上桥、行驶至跨中、一轮出桥三种工况,每种工况重复三次。
2 实验结果分析
2.1 时程响应分析
选取车辆20 cm高度滑落(通过桥梁时的速度约为1.98 m/s),一轮出桥时刻桥墩受到撞击的工况,与无撞击时车桥动力响应进行对比分析。
2.1.1 撞击力时程曲线
图5是实测撞击力的时程曲线。可以看出,撞击力近似呈现为三角形脉冲,作用时间很短,整个脉冲宽度只有0.02 s左右,主峰值时间大约0.002 93 s。
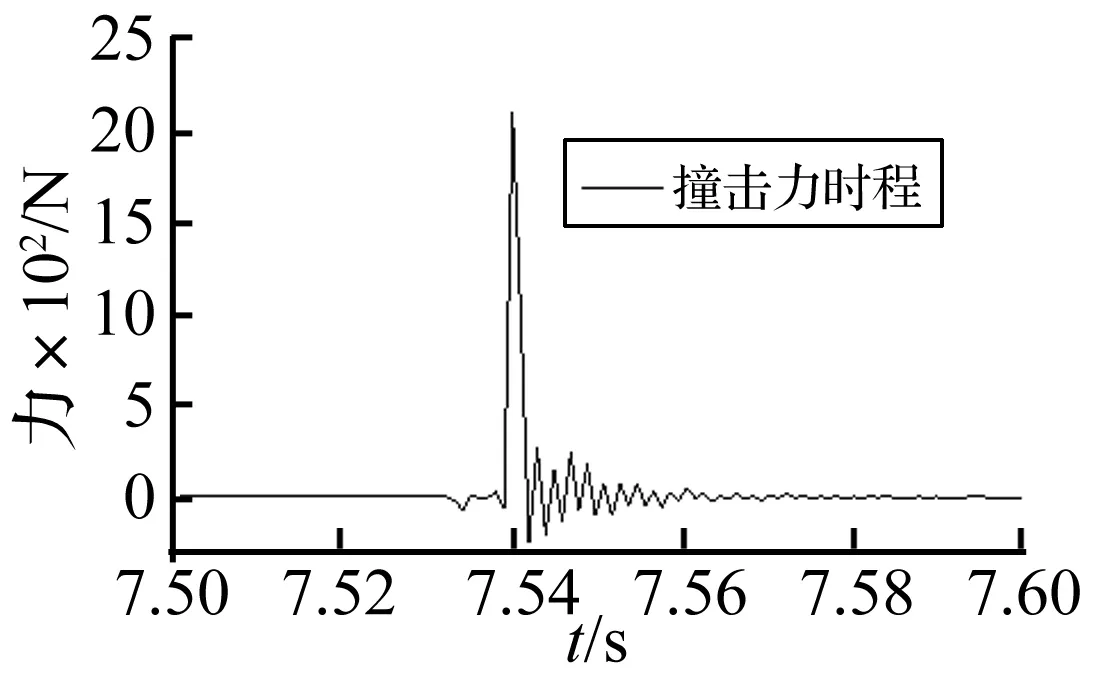
图5 撞击力时程
2.1.2 桥梁动力响应
图6为左、右墩顶的实测加速度时程曲线。可以看出,没有撞击时,墩顶横向加速度曲线比较平稳。撞击荷载作用下,被撞击的左墩墩顶加速度曲线中出现了明显的脉冲响应波形,峰值达到58.80 m/s2;右墩加速度变化不大,较无撞击时略有增大,为4.22 m/s2。
图7为梁1/4、1/2跨处的实测加速度时程曲线。可以看出,没有撞击时,梁横向加速度时程曲线比较平稳,但在车辆上下桥时有一定的冲击;有撞击时,梁1/4、1/2跨处横向加速度曲线中均出现了明显的响应脉冲波形,峰值分别达到68.57 m/s2、57.26 m/s2,离撞击点较近的1/4跨测点冲击响应加速度幅值较大。
图8、图9分别为左、右墩顶和梁1/4、1/2跨的横向位移时程曲线。
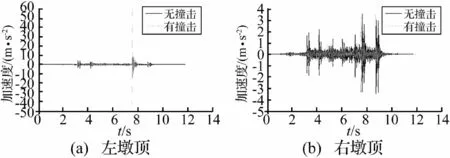
图6 墩顶横向加速度时程
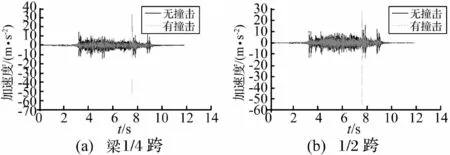
图7 梁横向加速度时程
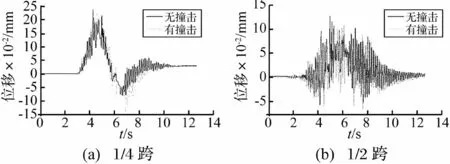
图8 墩顶位移时程曲线

图9 梁体横向位移
从图中可以看出,没有撞击时,墩顶横向位移曲线比较小,其中若干零散峰值的出现是轨道接头引起的。有撞击时,左墩顶位移波形中出现了明显的脉冲,峰值达到0.023 mm;右墩顶波形与没有撞击时变化不大,峰值为0.011 mm。
有无撞击时,梁体1/4跨和1/2跨的横向位移变化均不明显。
2.1.3 车辆动力响应
图10是实测车体中心的横向和竖向加速度时程曲线。
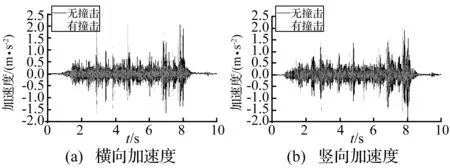
图10 车体加速度时程曲线
没有撞击时,车体横向、竖向加速度时程曲线比较平稳,轮对上下桥时波形有突起,峰值分别为1.18 m/s2、1.36 m/s2,曲线中其它峰值的出现主要是轨道接头引起的。撞击时刻发生在7.54 s,此时各向加速度曲线中均出现了明显的脉冲响应,峰值分别达到2.63 m/s2、1.42 m/s2,以横向最为明显,可见横向撞击力相对于车体横向加速度影响明显。
根据以上波形对比,可以看出,在撞击力作用下,除梁体横向位移外,其它动力响应指标显著增加。
2.2 桥车动力响应随撞击力的变化规律
此处选取车辆从26 cm高度释放(通过桥梁时的速度约为2.26 m/s),行驶至跨中时桥墩受到汽车撞击,测量各测点加速度最大值。
图11是左墩顶、梁跨中加速度最大值随撞击力的变化。可以看出:在撞击力小于5 kN时,墩顶和梁跨中加速度随撞击力明显增大,超过5 kN以后,加速度随着撞击力变化呈现离散形式,规律性不高,可能是因为传感器量程和局部振动原因。
图12是车体加速度最大值随撞击力的变化。可以看出,随着撞击力增大,车体加速度略呈上升趋势,车体中心加速度略大于后转向架加速度。
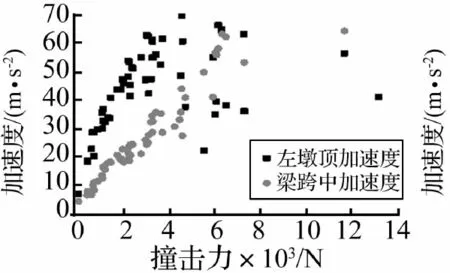
图11 左墩顶、梁跨中加速度随撞击力的变化

图12 车体加速度随撞击力的变化
3 等效静力计算
3.1 简化脉冲法介绍
根据Chopra[10],将车撞桥墩简化成无阻尼体系,其动力学方程如下:
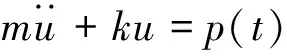
(1)
如果td(脉冲持续时间)小于Tn/2(结构周期一半),则体系的整体最大反应发生在它的自由振动阶段,并受脉冲的时间积分控制,与脉冲荷载形式无关,面积相同的三个脉冲力的冲击谱见图13。
随着脉冲持续时间与体系的固有周期相比变得非常短,脉冲变成纯冲量,其值可以表示为
(2)
体系对这个冲击力的反应是无阻尼体系反应的单位脉冲响应乘以I,即:
(3)
最大变形为
(4)
根据等效位移法定义,动力作用下体系产生位移u0,对应需要的静力Pa为
(5)

图13 面积相同的三个脉冲力的冲击谱
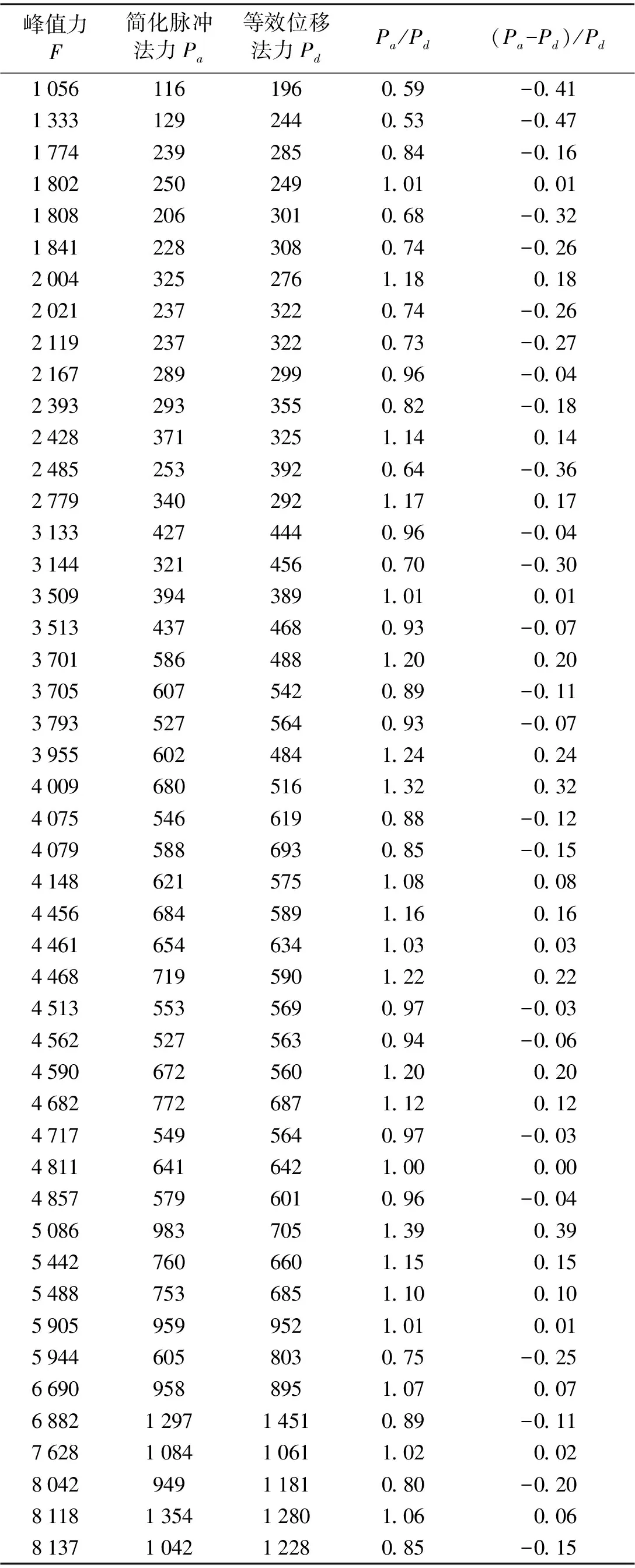
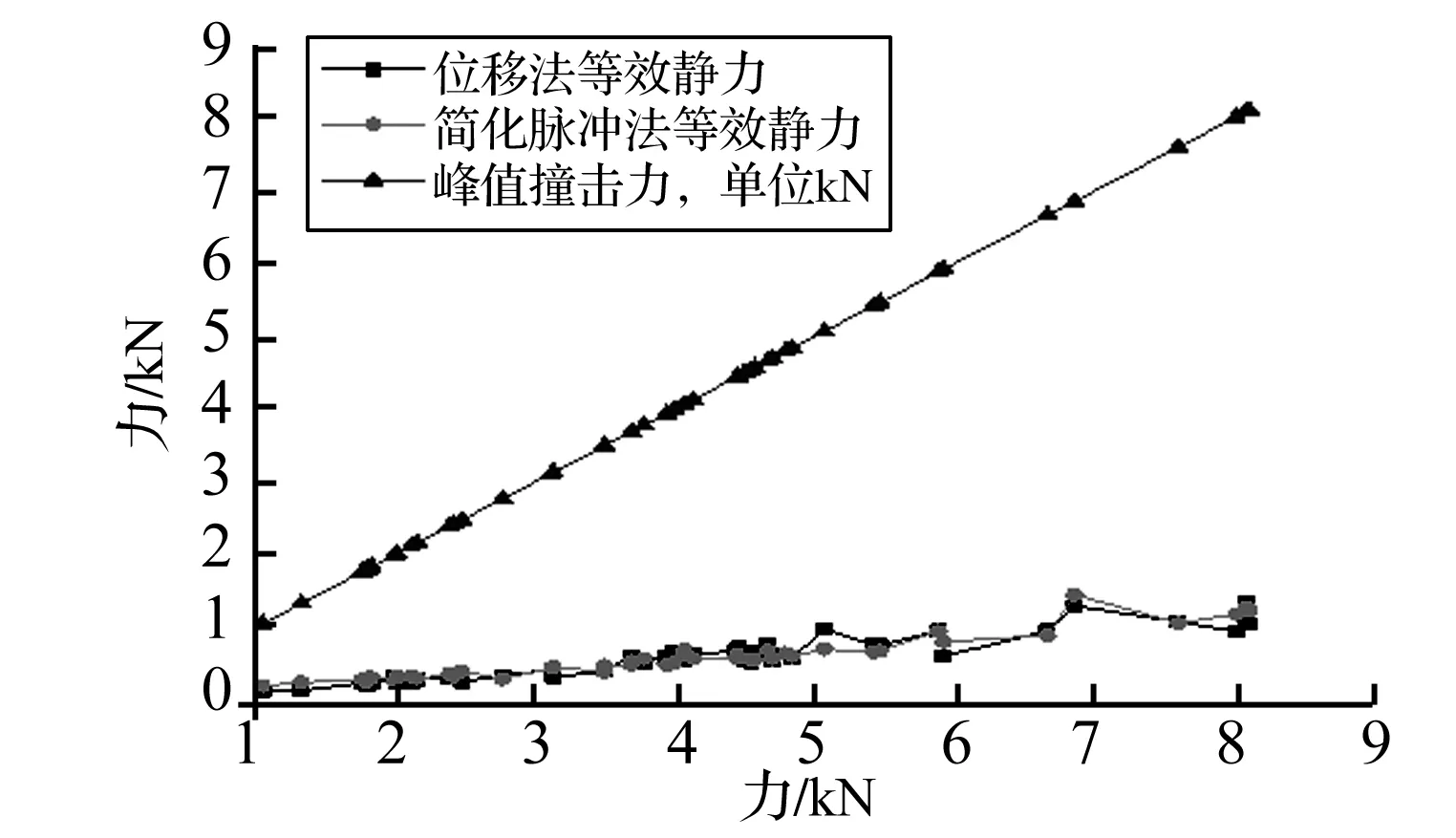
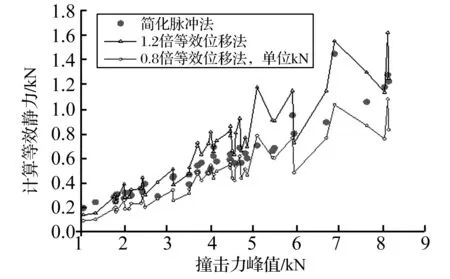
在图13中可以看出,在td 图中横坐标td/Tn为时间比值无量纲常数,纵坐标u0/(P0/k)为位移比值的无量纲常数。 美国密歇根大学的El-Tawil等[4]采用非线性有限元模拟技术研究了一辆66 kN的Ford卡车撞击桥墩作用过程。图14是卡车以135 km/h的速度撞击桥墩的撞击力时程曲线,峰值约为26.3 MN。 图14 一辆66 kN汽车撞击桥墩的撞击力时程 可以看出,整个撞击过程在0.16 s内结束,取td=0.16 s,在td/Tn小于1/2时,纯冲量解可以近似计算汽车撞击力的等效静力。本文通过模型试验来验证简化脉冲法在计算汽车撞击桥墩时瞬态撞击力的等效静力计算的准确性。 等效位移法[4]求等效静力是指在力作用点,和对应动力荷载产生相同位移时所需要静力的大小Pd。等效静力取决于系统的刚度和动力特性。每一次撞击过程中墩顶最大位移取为y,墩身刚度为k,按下式计算等效撞击力 Pd=ky (6) 式中:y为墩顶动位移最大值;k=EI,E为钢材弹性模型,I为桥墩截面惯性矩。 理论上认为这是等效静力的真实值,可以作为评判简化脉冲法计算等效静力有效性的标准。 用Midas建立桥梁模型,进行模态分析,得出一阶频率为桥墩横向振动主频,频率为12.77 Hz,如图15。 提取墩顶位移时程做一次微分得到速度时程,做快速傅里叶变换(FFT),得到桥墩频谱响应,桥墩横向振动主频为13 Hz,见图16。 图15 Midas模态分析 图16 加速度频谱图 采取实测值13 Hz作为本桥墩的横向振动主频。撞击力时程曲线中撞击力作用时间td主要集中0.02 s内,取td=0.02 s,Tn=1/f=0.077 s,td<1/2Tn=0.038 5 s,因此可以采样简化脉冲法计算本模型试验中瞬态撞击力的等效静力。 用Matlab语言编写程序,对撞击力时程进行积分,利用式(5)求解等效撞击力。 表1为分别采用简化脉冲法和等效位移法计算的等效静力汇总结果,表中同时给出了峰值撞击力值。 把等效位移法、简化脉冲法计算的等效静力、撞击力峰值绘于图17。通过表1、图5、图17可以看出:尽管峰值撞击力很大,但撞击过程是瞬态的,撞击全程时间大约只有0.02s,呈近似三角脉冲形式,等效静力约为峰值力的10%~20%,并且简化脉冲法和等效位移法计算的等效静力值有良好的一致性。 表1 二种等效静力方法计算结果的比较(单位:N) 图17 等效静力汇总图 将1.2倍和0.8倍等效位移法计算的等效静力作为平行包络线的上限和下限,将简化脉冲法计算的等效静力绘于图18。 图18 简化脉冲法计算等效静力包络图 通过表1和图18可以发现,在峰值力为1 056 N和1 033 N时,对应的简化脉冲法计算的等效静力值明显超出包络线,但其它等效静力值基本包含在包络线内,说明撞击力越大,试验效果越好,简化脉冲法计算等效静力越接近于真值,激励不充分的情况下,计算值可能会偏离真值。因此,保守的取1.2倍简化脉冲法计算的等效静力作为结构承受的静力供工程设计参考。 本文通过模型试验,获得了有无汽车撞击桥墩时桥梁、车辆动力响应变化,选取部分实验结果对进行对比分析,最后用简化脉冲法计算瞬态撞击力的等效静力,并与等效位移法计算的等效静力做比较,得出了以下结果和结论: (1)撞击力对桥梁动力响应有明显的影响。在撞击力作用下桥梁横向加速度和动位移幅值是无撞击作用下的数十倍,桥墩、梁1/4跨、梁1/2跨处动力响应依次减弱,离撞击点越近,动力响应越明显。 (2)桥梁在撞击力作用下产生动力响应,可以有效传递到车辆上,加速度峰值是无撞击时的1.5~3倍,并且对车辆横向加速度影响最为明显。 (3)撞击荷载呈现近似三角形脉冲形式,所以当撞击作用时间小于被撞结构周期一半,即td/Tn<1/2,或者桥墩频率f<1/2td时,可以使用简化脉冲法计算等效静力Pa,为了确保结构安全,可以设置一个1.2的安全系数,即1.2Pa作为瞬态撞击力的等效静力。 (4)等效静力约为撞击力峰值的10%~20%,激励越充分,实验效果越好,简化脉冲法计算等效静力越接近于真值,激励不充分的情况下,计算值可能会偏离真值。 桥梁车撞力受很多复杂因素的影响,本文通过模型试验定性的初步探讨了横向撞击力对桥梁结构及桥上行车安全的影响。由于试验条件的限制,缩尺实验与足尺实验的材料属性相似关系也未明确,汽车采用了简单的刚体模型,今后将进一步探讨相似相容关系[11-12],使其能够模拟车头在撞击时的塑性变形特点。 [1]何水涛,陆新征,卢啸,等.超高车辆撞击钢桥上部结构模型试验研究[J].振动与冲击,2012,31(5): 31-35. HE Shui-tao,LU Xin-zheng,LU Xiao,et al.Tests for collision between over-high trucks and steel bridge superstructures[J].Journal of Vibration and Shock,2012,31(5): 31-35. [2]夏超逸,雷俊卿,张楠.流冰撞击力作用下列车-简支梁桥耦合振动分析[J].振动与冲击,2012,31(13): 154-158. XIA Chao-yi,LEI Jun-qing,ZHANG Nan.Coupled vibration analysis for train and simply supported bridge system subjected to floating ice collision[J].Journal of Vibration and Shock,2012,31(13): 154-158. [3]Derucher K N.Analysis of concrete bridge piers for vessel impact[J].Civil Engineering for Practicing and Design Engineers,1982,1(4): 393-420. [4]Sherif EI-Tawil P E M,ASCE,et al.Vehicle Collision with piers[J].Journal of Bridge Engineering,2005,10(3): 345-353. [5]夏超逸,张楠,夏禾.汽车撞击作用下车桥系统的动力响应及高速列车运行安全分析[J].工程力学,2013,30(8): 119-126. XIA Chao-yi,ZHANG Nan,XIA He.Dynamic responses of train-bridge system subjected to truck collision and running safety evaluation of high-speed train[J].Engineering Mechanics,2013,30(8): 119-126. [6]Xia C Y,Lei J Q,Zhang N,et al.Dynamic analysis of a coupled high-speed train and bridge system subjected to collision load[J].Journal of Sound and Vibration,2012,331(10): 2334-2347. [7]中华人民共和国行业标准.高速铁路设计规范(试行)(TB10621-2009)[S].北京:中国铁道出版社,2009. [8]British Standard BS EN1991-1-7:Eurocode 1-Actions on structures General action: accidental actions[S].2006. [9]AASHTO I.RFD.AASHTO LRFD bridge design specifications[S].Washington,D.C.,2007. [10]Chopra A K.Dynamics of structures: Theory and applications to earthquake engineering(2nd Ed)[M].New Jersey: Prentice Hall,2001. [11]雷正保,钟志华.动态大位移大转角大变形弹塑性相似结构的相似比[J].机械工程学报,1999,35(2): 6-9. LEI Zheng-bao,ZHONG Zhi-hua.Similitude ratios of elastic-plastic similitude structure with large displacement and large deformations for dynamic system[J].Chinese Journal of Mechanical Engineering,1999,35(2): 6-9. [12]雷正保.汽车结构的大变形动态相似准则及相似计算精度[J].实验力学,2000,15(4): 429-435. LEI Zheng-bao.Dynamic similarity criteria for automotive structures of elastic-plastic materials under large deformation condition and precision of similarity calculation[J].Journal of Expermental Mechanics,2000,15(4): 429-435. [13]朱亚迪,卢文良.小车墩柱撞击力模型实验研究[J].振动与冲击,2013,32(21): 182-185. ZHU Ya-di,LU Wen-liang.Model tests for collision force between a vehicle and piers[J].Journal of Vibration and Shock,2013,32(21): 182-185. [14]雷正保,李丽红,雷沐羲,等.新型柔性护栏碰撞安全性仿真分析及实车验证[J].振动与冲击,2013,32(22): 28-31. LEI Zheng-bao,LI Li-hong,LEI Mu-xi,et al.Simulation analysis and real car validation for crashworthiness of a new flexible safe fence[J].Journal of Vibration and Shock,2013,32(22): 28-31.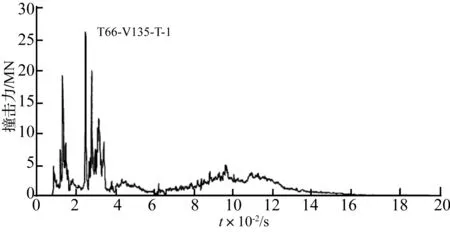
3.2 评判标准——等效位移法
3.3 简化脉冲法在本模型试验中的适应性


3.4 简化脉冲法与等效位移法计算等效静力对比分析
4 结 论
