过程阻尼对铣削系统稳定性的影响

李 欣，李 亮，何 宁

(南京航空航天大学 机电学院，南京 210016)

铣削加工广泛应用于航空、航天、模具等行业，再生型颤振是制约其表面加工质量和零件精度的关键因素。它给工件留下明显的斜状振纹和较大的粗糙度，往往需要手工珩磨去除，严重的甚至直接导致工件报废。控制颤振的方法一般均可归结为增加系统阻尼。切削系统阻尼可分为机床结构阻尼和由加工刀具后刀面与工件表面相互干涉而产生的阻尼，亦称为过程阻尼(process damping)。过程阻尼的分析和建模是近年国际学术界的研究热点，加拿大Altintas等[1]曾将其列为切削颤振中尚未解决的研究难点。目前国内的相关文献很少，在大多数研究中，铣削稳定性分析都采用较为传统的线性模型[2-3]，未考虑过程阻尼，该模型在低速区会产生很大误差。

Sission和Tlusty等[4-6]最早发现切削加工中的过程阻尼现象，随着切削速度降低，车削加工的稳定性极限可显著提高。Sission等[4]还归纳出，切削速度，刀具后角和刃口半径是影响过程阻尼的关键因素。后来诸多学者针对过程阻尼进行研究，指出后刀面与工件表面振动波纹干涉形成的作用力，是过程阻尼的来源[7-10]。文献[11-12]通过大量动态切削实验，识别动态切削力系数，进而标定过程阻尼系数，这种阻尼建模方法，工作量大，对实验精度要求很高。Budak等[13-15]提出了较为简便的阻尼系数识别方法，将稳定性极限预测的解析法与实测极限切深相结合，标定过程阻尼系数。

目前，对于过程阻尼的研究，主要集中在车削方面，铣削加工的过程阻尼分析，依然是个难点。其自由度多，受力分析需要坐标转换，动力学方程中存在时变系数，对于侵入面积和过程阻尼力的描述远较车削困难。

本文旨在建立一考虑过程阻尼的铣削动力学模型，引入坐标变换，计算刀具后刀面与工件振动波纹的侵入面积以及干涉阻力，分析过程阻尼对系统稳定性极限的影响，并通过铣削实验来验证本文模型。

1 过程阻尼形成机理

在切削加工中，如果颤振发生，振幅增大，这时后刀面与工件的犁耕效应增强，发生干涉，形成侵入面积，阻力增大，会对颤振产生抑制作用，如图1(a)所示。按照传统的线性模型，颤振发生以后，振幅是发散的，但是由于后刀面干涉形成的阻力，系统振荡不会发散，而是形成极限环，振动能量能够被控制，过程阻尼由此而来，而相应的阻力可被称为过程阻力。

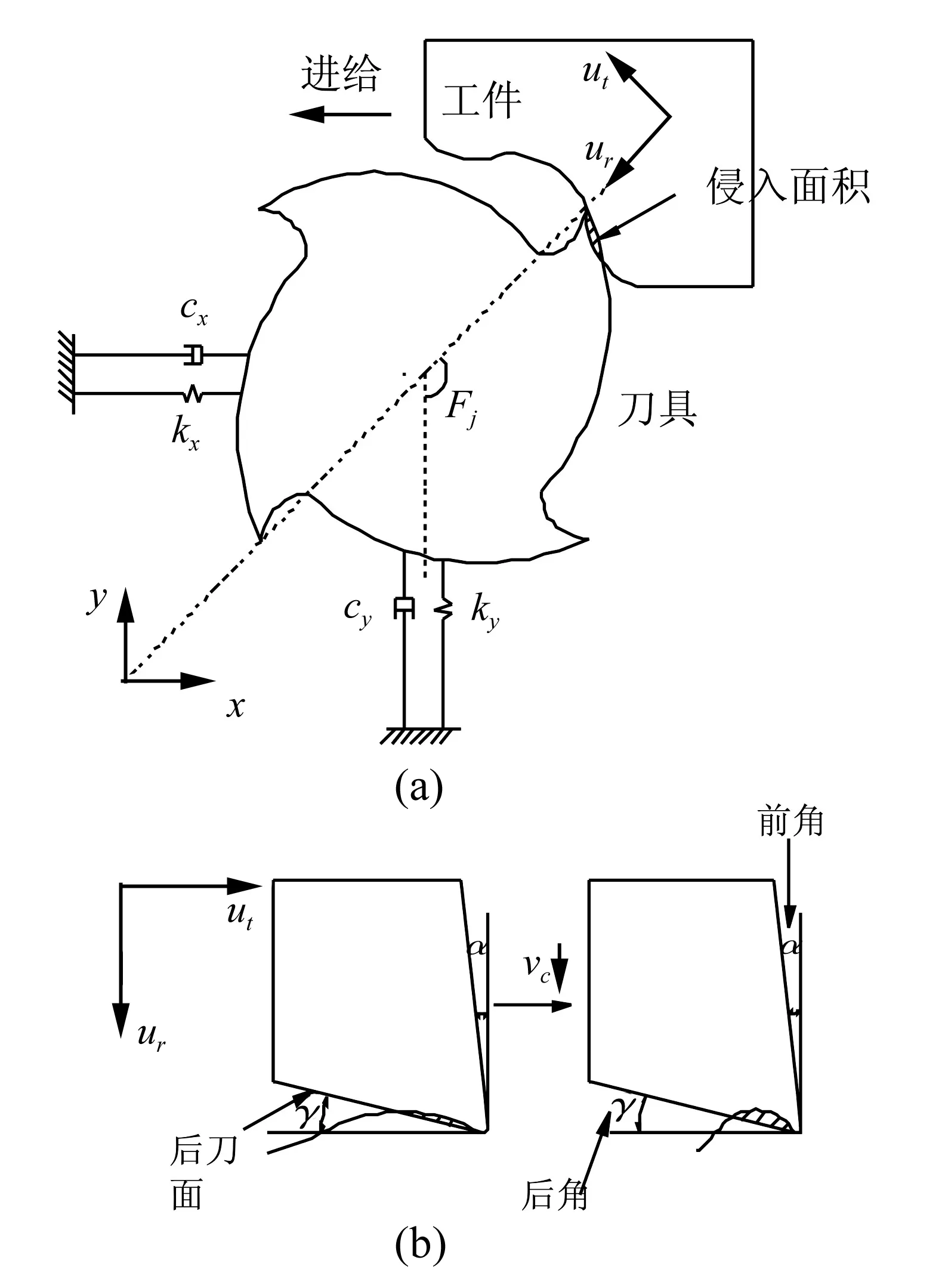
图1 过程阻尼形成机理示意图

侵入面积的计算是个难点，需要在整体坐标系下，迭代计算振动位移的同时，变换坐标系，计算径向的振动位移ur，判断后刀面与工件表面波纹是否发生干涉，搜索后刀面与波纹的交点位置，如图2所示。

图2 侵入面积计算示意图

当判断出交点位置后，开始叠加计算侵入面积

(1)

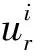
2 铣削动力学方程

对于铣削加工，计入过程阻尼的动力学方程

(2)

式中:{FxpFyp}T即为整体坐标系下的过程阻力，若不将其计入，即为线性模型。(mx,my)，(cx,cy)，(kx,ky)分别为主轴-刀具系统的结构质量、阻尼、刚度参数，可通过模态实验获取。

作用于刀具的动态切削力为各个刀齿的切削力之和，即:

(3)

式中:N为刀齿数，单个刀齿的切削力为[2]

(4)

式中:C=cos(φj)，S=sin(φj),φj为切削刃的径向接触角，φj=Ωt，Ω为主轴转速，ap为轴向切深，Kt为切向力系数，Kr为切向力系数，ft为进给量。T为刀齿周期。(x(t),y(t))为当前刀齿周期的振动位移，称为内调制，(x(t-T),y(t-T))为前一个刀齿周期的振动位移，称为外调制，内调制和外调制之间的相位差即为再生型颤振的根源[2]。

方程(2)的求解，采用隐式龙格库塔法，计算流程如图3所示,相关说明如下：

(1)初始化数据。包括切削系统动力学参数，刀具几何角度，进给，刀具初始位置，切出切入角，切削力系数，需要的仿真周期，轴向切深，主轴转速，计算步长。将刀具振动位移，速度和切削力置0。

(2)开始运行程序，计算刀具振动位移x(t)，y(t)，以及振动速度、切削力，需同时进行坐标转换，计算径向振动位移xr(t),yr(t)，判断干涉是否发生。一般在最开始的几个周期，振动位移比较小，干涉不会发生，振动主要由动态切削力引起。

图3 计算流程示意图

(3)在计算振动位移的同时，需要记录动态切屑厚度。对于给定工况，得到足够的时域数据后，可以按照文献[16]提供的颤振判定法，最大动静态切屑厚度比hd,max/hx,max>1.7时，即可视为颤振发生。在给定切宽和转速下，逐步增大轴向切深，由该判定法确定稳定性极限。

3 实验分析

为验证过程阻尼现象，同时进行了仿真(基于matlab编程)和实验分析，将传统的线性模型与本文模型进行对比。

实验设备：

机床：Mikron UCP DURO710五坐标加工中心

刀具：整体硬质合金立铣刀，全长125 mm，悬长70 mm，刃长30 mm，直径12 mm，4齿，后角15°。

传感器：测振：压电加速度传感器3035B1G(IEPE型)

测声：BSWA传声器MP201。

工件：铝合金材料T6061，尺寸75 mm×75 mm×45 mm。

切削力系数：切向力系数Kt=728 MPa，径向力系数Kr=245 MPa，由铣槽快速标定法[17]获得；

过程阻力系数(对于铣削加工时，常用航空铝合金材料的过程阻力系数标定，文献[14]有过相关报道)：侵入力系数Kd=40 000 N/mm3,摩擦力系数μ=0.3[14]，该组系数的获取难度较大，尤其是侵入力系数，需通过切削实验结合振动理论来标定[14]。

主轴-刀具系统结构模态参数见表1。

表1 主轴-刀具系统结构模态参数

实验分别在高速区和低速区进行，切宽取2 mm，进给0.1 mm/z，顺铣，而对于仿真，设定的运算周期数为30。图4为在高速区(>5 000 r/min)，按照不计过程阻尼的线性动力学模型，绘制的稳定性叶瓣图及实验分析结果。实验结果与线性动力学模型吻合较好。谱分析结果显示，随着轴向切深增大，颤振频率对应的峰值变得突出，预示着颤振发生，在主轴转速n=10 000 r/min时，颤振频率ωc比结构固有频率略大，为1 167 Hz，而相位β=ωcT(T为刀齿通过周期)约为1.5π，属于Hopf分叉[18]，这是最常见的失稳形式。

图4 颤振稳定性分析示意图(高速区)

图5为在低速区(<5 000 r/min)，分别按照线性动力学模型和计入过程阻尼的非线性模型绘制的稳定性叶瓣图。从中可以看出，在低速区，过程阻尼的影响体现了出来，按照线性动力学模型，在低速区很难有完整的稳定性叶瓣，稳定性极限很低。而如图4所示，计入过程阻尼之后，相比于线性模型，稳定区域显著增加，分析结果产生了很大差异。在远超线性模型稳定性极限的实验点处(轴向切深ap=8 mm，主轴转速n=1 000、2 000 r/min)，加工过程非常平稳，产生的声音也较为平缓。

图6～7为实验中不同工况下采集的加速度和声信号峰值。可以看出随着切削速度降低，声信号和加速度信号都大大减弱，工况(n=2 000 r/min,ap=8 mm)处的声信号和加速度峰值尚不及工况(n=1 0000 r/min,ap=1 mm)时的峰值，过程阻尼的作用体现得非常明显。

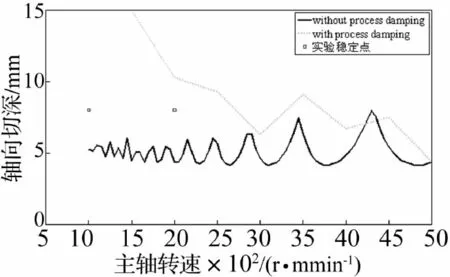
图5 颤振稳定性分析示意图(低速区)

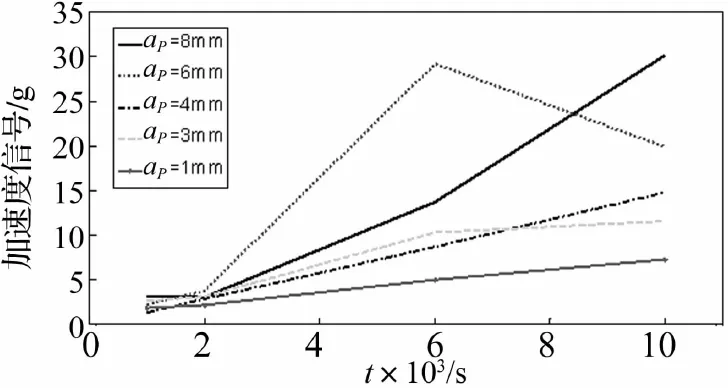
图6 不同工况的加速度峰值

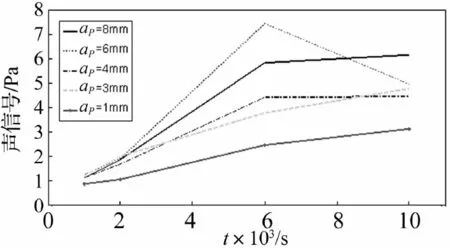
图7 不同工况的声信号峰值

(a)(n=10 000 r/min) (b)(n=6 000 r/min) (c)(n=2 000 r/min)

与此同时，如图8所示，同一切深(ap=8 mm)下，随着切削速度的降低，加工表面的振纹也产生了比较明显的变化，当n=10 000 r/min及6 000 r/min时,加工表面呈现右旋状的斜纹，这是因为再生型颤振发生时，内调制与外调制存在相位差β∈[π，2π)[18]，这时系统是不稳定的。而当n=2 000 r/min时，加工表面呈现直纹，这时相位差β=2π，前后两个刀齿切削过程的波动形式一致，系统振动属于强迫振动，再生型颤振得到抑制，系统处于稳定区[18]。振纹的变化表明，过程阻尼可显著提高系统稳定性。

4 结 论

(1)本文建立了考虑过程阻尼的非线性铣削动力学模型，计算由犁耕效应形成的侵入面积，以及过程阻力。通过时域仿真方法计算临界切深。仿真和实验结果均显示，在低速区，过程阻尼作用体现得非常明显，相对于常用的线性模型，稳定性区域显著增加。

(2)过程阻尼现象，对于难加工材料铣削参数的选择有一定帮助。为保证刀具寿命，难加工材料基本以较低速度进行切削。这是如果按照传统的线性模型，稳定性极限很低，对加工非常不利。通过调整转速和刀具几何角度，利用过程阻尼来控制颤振，是一种有效的方法。

[1]Altintas Y，Weck M.Chatter stability in metal cutting and grinding[J].Annals of the CIRP，2004,53(2):619-642.

[2]Altintas Y.数控技术与制造自动化[M].北京:化学工业出版社,1977.

[3]Altintas Y，Stepan G.Chatter stability of milling in frequency and discrete time domain[J].CIRP Journal of Manufacturing Science and Technology，2004,53(2):619-642.

[4]Sisson T R，Kegg R L.An explanation of low-speed chatter effects[J].ASME Journal of Engineering for Industry,1969,91:558-951.

[5]Tlusty J.Analysis of the state of research in cutting dynamics[J].Annals of the CIRP，1978，27(2):583-589.

[6]Tlusty J，Ismail F.Special aspects of chatter in milling[J].ASME Journal of Engineering for Industry，1983，105:24-32.

[7]Wu D W.A new approach of formulating the transfer function for dynamic cutting process[J].ASME Journal of Engineering for Industry，1989,111:37-47.

[8]Elbestawi M A,Ismail F，Du R，et al.Modeling machining dynamic including damping in the Tool-Workpiece interface[J].ASME Journal of Engineering for Industry，1994,116:435-439.

[9]Lee B Y，Tarng Y S，Ma S C.Modeling of the process damping force in chatter vibration[J].International Journal of Machine Tools and Manufacture，1995,35(7):951-962.

[10]Shawky A M，Elbestawi M A.An enhanced eynamic model in turning including the effect of ploughing forces[J].ASME Journal of Manufacturing Science and Engineering，1997,119(1):10-20.

[11]Peters J，Vanherck P，Brussel Van.The measurement of the dynamic cutting coeffient[J].Annals of the CIRP，1971，21(2):129-136.

[12]Altintas Y，Eynian M，Onozuka H.Identification of dynamic cutting force coefficients and chatter stability with processdamping[J].CIRP Annals-Manufacturing Technology，2008,57:371-374.

[13]Budak E，Tunc L T.A new method for identification and modeling of process damping in machining[J].Journal of Manufacturing Science and Engineering，2009,131:1-10.

[14]Budak E，Tunc L T.Identification and modeling of process damping in turning and milling using a new approach[J].CIRP Annals-Manufacturing Technology，2010,59:403-408.

[15]Tunc L T，Budak E.Effect of cutting conditions and tool geometry on process damping in machining[J].International Journal of Machine Tools and Manufacture，2012,57:10-19.

[16]Campomanes M L，Altintas Y.An improved time domain simulation for dynamic milling at small radial immersions[J].Transactions of ASME Journal of Engineering，2003,125:416-422.

[17]刘强，李忠群.数控铣削加工过程仿真与优化[M].北京:航空工业出版社,2011.

[18]宋清华.高速铣削稳定性及加工精度研究[D].济南：山东大学,2009.