真型试验线路六分裂导线舞动模拟

周林抒，严 波，杨晓辉，吕中宾

(1.重庆大学 航空航天学院，重庆 400044；2.河南省电力公司 电力科学研究院，郑州 450052；3.上海交通大学 电气工程系，上海 200030)

近年来，我国河南、河北、湖北、湖南、山东和辽宁等地的输电线路曾发生大面积舞动现象，造成线路跳闸、金具破坏，甚至杆塔坍塌，对国民经济带来重大危害。因此，在我国输电线路的舞动及其防治技术的研究已引起高度重视。

利用真型试验线路研究覆冰导线的舞动及其防治技术在国际上早已引起重视，如日本在敦贺建立了档距为347 m的两档四分裂导线和八分裂导线试验线路，对导线的舞动进行了长期观测[1-2]。Dyke等[3]在加拿大魁北克水电公司的试验线路上安装D形人工覆冰模型，研究覆冰导线的舞动及其防治技术。2010年，我国国家电网公司在河南省郑州市西南方向的尖山地区建立了真型输电线路综合试验基地。在部分试验线路段导线上安装了人工覆冰模型，并在试验线路上成功模拟了舞动现象。该试验线路为输电线路的舞动及其防治技术的研究提供了重要的试验场所。

利用真型试验线路研究覆冰导线的舞动技术防治技术，由于试验现场的风速和风向等条件的不可控制性，模拟试验受自然条件的限制较大，试验效率往往不高。为此，通过建立该真型试验线路的数值模型，预先利用数值方法模拟导线的舞动以及不同防舞技术的防舞效果，从而为现场试验提供合理的试验方案，对于提高试验效率具有重要的意义。关于覆冰导线舞动的数值模拟研究已有不少研究成果[4-7]，这些工作的计算模型中一般未考虑杆塔的作用。Baenziger等[8]利用简化模型给出了导线舞动过程中导线对杆塔的作用力的简单计算式，但其没有考虑塔线体系中导线和杆塔的耦合作用，和实际相去甚远。李黎等[9]建立了六分裂导线两塔三档有限元模型，模拟研究了输电塔线耦合体系中导线的舞动，模型中将分裂导线等效为单导线，给出了导线舞动过程中杆塔的受力和变形，但未对考虑杆塔变形后覆冰导线的舞动特征进行分析。利用该模型，曹华锦等[10]进一步模拟研究了相间间隔棒和压重防舞效果。最近，赵莉等[11]建立了两塔三档输电线耦合体系精细有限元模型，模拟研究了杆塔变形对覆冰四分裂导线舞动特征的影响。

本文针对我国河南尖山真型试验线路段，建立塔线耦合体系精细有限元模型，数值模拟在现场实测风速作用下，安装了D形覆冰模型的六分裂导线线路段的舞动过程。通过数值模拟得到的导线舞动轨迹、响应特征以及导线中张力的变化与实测结果的比较，验证数值模型及舞动模拟方法的正确性。利用该数值模型，可以进一步对各种防舞器的布置方案和防舞性能等进行模拟评估，为现场试验方案的指定提供依据，具有重要的实用价值。

1 真型试验线路及舞动模拟试验

我国国家电网公司在河南新密市尖山建立的真型输电线路综合试验基地于2010年8月建成并投入使用。试验线路全长3 715 m，线路为东西走向，共有10个杆塔，杆塔从西到东依次编号，档距在157 m～657 m之间。其中紧凑型线路段2 723 m，综合试验段992 m，采用水平、垂直、三角形等导线布置方式，可悬挂110 kV～1 000 kV不同分裂数的导线，现场监测站设有监控中心及相关试验室。该试验基地建成后主要用于开展输电线路舞动、振动特性观测、机理研究及防舞、防振、防风偏装置评估与优化研究。

图1 真型试验线路段

目前投入试验的线路段为2号塔与5号塔之间的线路。2号塔和5号塔之间依次为第2档、第3档和第4档。第2档架设单导线、双分裂、三分裂和四分裂导线；第3和4档架设三相六分裂导线。图1所示为试验线路段。为了模拟研究六分裂导线的舞动，在第3档的所有六分裂导线上安装了人造D形覆冰模型，覆冰模型用PVC塑料制作，安装角度开口侧朝南向上60°。安装了D形覆冰模型的六分裂导线如图2所示。

2011年6月3日下午5点，在自然风激励下，该档六分裂导线发生了竖向振动幅值超过4 m的舞动，一直持续到夜间12点，这是我国首次在真型试验线路上成功模拟舞动。之后，试验线路上舞动事件时有发生。

图2 安装D形覆冰模型的六分裂导线

2 六分裂线路段有限元模型

以真型试验线路中六分裂线路段为研究对象，建立包括第2、3、4档的两塔三档模型。采用ABAQUS有限元软件建立模型。

2.1 塔线耦合模型

第2、3、4档的档距分别为536 m、284 m和588 m。导线型号为LGJ-300/40，地线为GJ-80钢绞线，导线和地线的物理参数如表1所列。3号塔为耐张塔，4号塔为直线塔，塔高分别为56.9 m和43.7 m，两塔间的地形高差为19.3 m。两杆塔均由Q235和Q345材料组成。六分裂导线采用V型绝缘子串悬挂。

表1 导地线的物理参数

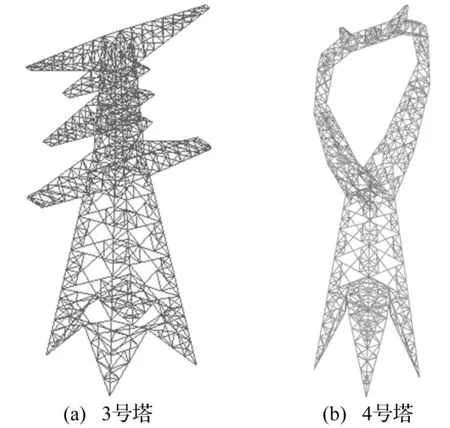
图3 杆塔有限元模型

有限元模型中，覆冰导线采用具有扭转自由度的索单元模拟，在ABAQUS中可通过释放空间梁单元结点的弯曲自由度，保留扭转自由度，将材料性质设置为不可压缩来模拟这种索单元[7]。对于未安装覆冰模型的导线和地线，在风荷载作用下不会发生扭转变形，故可用杆单元模拟，并设置其材料为不可压。绝缘子串采用杆单元模拟，而将间隔棒简化为框架，用空间梁单元模型。采用空间梁单元和杆单元离散杆塔，建立杆、梁混合有限元模型。

建立的杆塔和塔线耦合体系有限元模型分别如图3和4所示。模型的位移边界条件设置为：杆塔塔腿根部固定约束，线路段两端处的导线和地线固定约束。

利用严波等[12]提出的一种无需迭代的方法，确定导线和地线在自重作用下的初始构形。

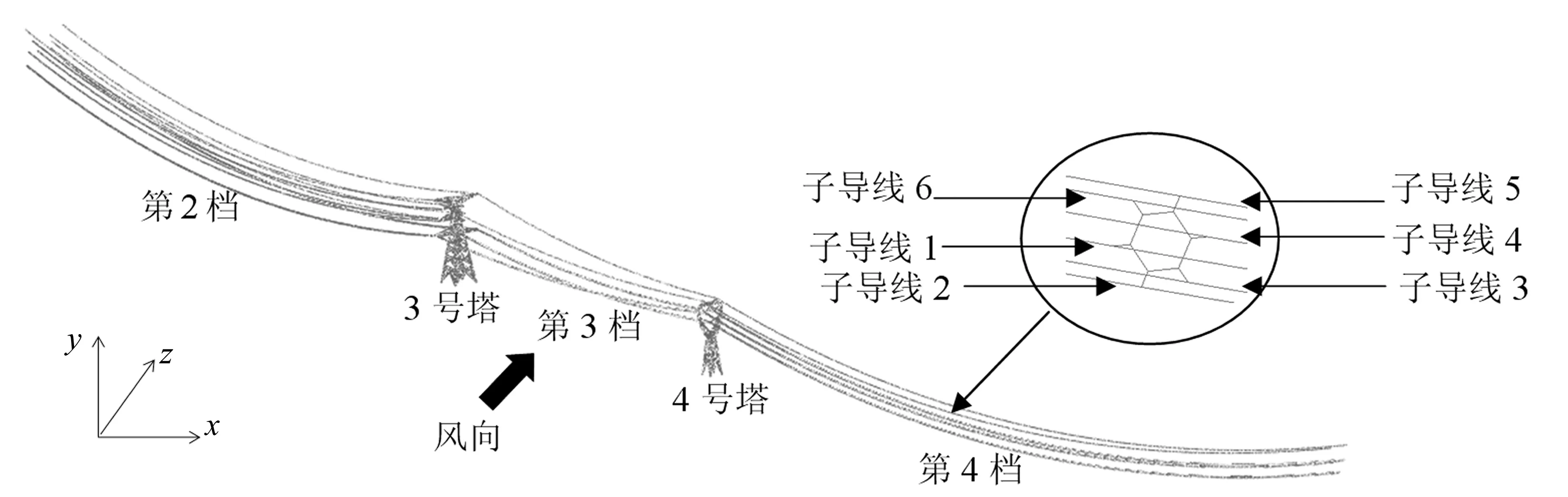
图4 塔线体系有限元模型

2.2 覆冰导线上的气动载荷

六分裂线路段的第3档三相共18根子导线上安装了D形覆冰模型。作用在这些子导线上的气动载荷有升力FL、阻力FD和扭矩M，由下式计算

[FLFDM]T=

(1)

式中:ρair和U分别为空气密度和来流风速；d为导线的直径；CL、CD、CM分别为升力系数、阻力系数和扭矩系数，由风洞试验测得，由于考虑尾流影响，各子导线的气动力系数不同；α为风攻角，与导线上覆冰初始凝冰角、导线的转动、横向运动以及风向等有关[4]。

2.3 裸导线和地线上的风载荷

对于未安装覆冰模型的裸导线和地线，其上仅作用风压荷载，按规范可由下式计算[13]:

(2)

式中:a为电线风压不均匀系数；μSC为电线体型系数；μz为风压高度变化系数；d为电线外径(mm)；Lp为电线水平档距(m)；U为基准高处的设计风速(m/s)；B为覆冰时风荷载增大系数；θ为风向与电线轴向间的夹角；W0为基准风压标准值(kN)。

2.4 杆塔和绝缘子串上的风荷载

作用于输电塔体的风荷载WS按下式计算[13]:

WS=W0μzμsβzBAs

(3)

式中:μs为构件风载体形系数；βz为杆塔风振系数；As为构件承受风压面积计算值(m2)。根据高耸结构设计规范[14]，风振系数按下式确定

βz=1+ξε1ε2

(4)

式中:ξ为脉动增大系数；ε1是考虑风压脉动和风压高度等的影响系数；ε2为振型、结构外形的影响系数[15]。

作用于绝缘子串上的风荷载标准值按下式计算[14]

Wl=W0μzBAl

(5)

式中:AI为绝缘子串的受风面积(m2)。

3 舞动数值模拟及其与实测结果的比较

为便于与实测结果的比较，模拟在现场实测风速下安装D形覆冰模型的六分裂导线的舞动。由于现场条件限制，目前仅在3号塔上与中相导线连接处测试记录风速。在发生舞动时某一段风速时程曲线及其对应的风速谱如图5所示。可见，风速随时间随机变化，该段实测风速的平均值为6.3 m/s。由其风速谱可见，实际风的能量集中在低频范围。

图5 发生舞动时某段实测风速时程及其风速谱

实际中，沿线路方向各点的风速存在差异，由于目前还难以获得沿线路各个位置处的风速时程，在此忽略这些点的风速时程差异，假设各点的风速与图5中所示相同，模拟六分裂导线在该风速时程作用下的舞动。值得一提的是，数值模拟过程中，在安装覆冰模型的导线上施加由式(1)确定的空气动力载荷，而其它裸导线和地线上则仅施加由式(2)计算的风压载荷。另外，作用于杆塔和绝缘子串上的载荷则分别由式(3)和(5)计算。

3.1 导线舞动响应

数值模拟得到该试验线路段在实测风速作用下的动力响应。试验中，采用单目测量技术记录了第3档六分裂导线中相靠近3号塔第一个间隔棒位置的舞动轨迹。为便于比较，图6给出由数值模拟得到的该点处子导线1的位移时程曲线，可以看出，导线的竖向振动幅值较大，水平方向振幅较小。在随机风作用下，导线的响应包含了强迫振动和自激振动[1-2]。

图6 第3档中相子导线1上靠近3号塔第一个间隔棒处的位移时程数值模拟结果

图7给出了数值模拟和现场实测得到的实测点处的舞动轨迹。数值模拟与现场实测数据选取的参考点不同，因此导线的平衡位置不同。数值模拟和实测导线舞动的最大垂直振幅相差较小，而最大水平振幅相差较大；舞动轨迹存在较明显的差异，但总的趋势较一致。造成这些差异的主要原因包括：①数值模拟中仅利用一个点的实测风速作为输入，未考虑实际风速的空间分布特性；②数值模拟中认为风垂直作用于塔线体系，实际风向不一定完全垂直于顺线路方向；③覆冰模型的实际安装角度可能存在偏差，因而会导致气动特性的变化；④现场测量误差等。

图8给出了由数值模拟得到的迎风相导线靠近3号塔第一个间隔棒处以及2/5间档距处导线的舞动轨迹。可以看出，不同相和同相不同位置处导线的舞动轨迹并不相同。

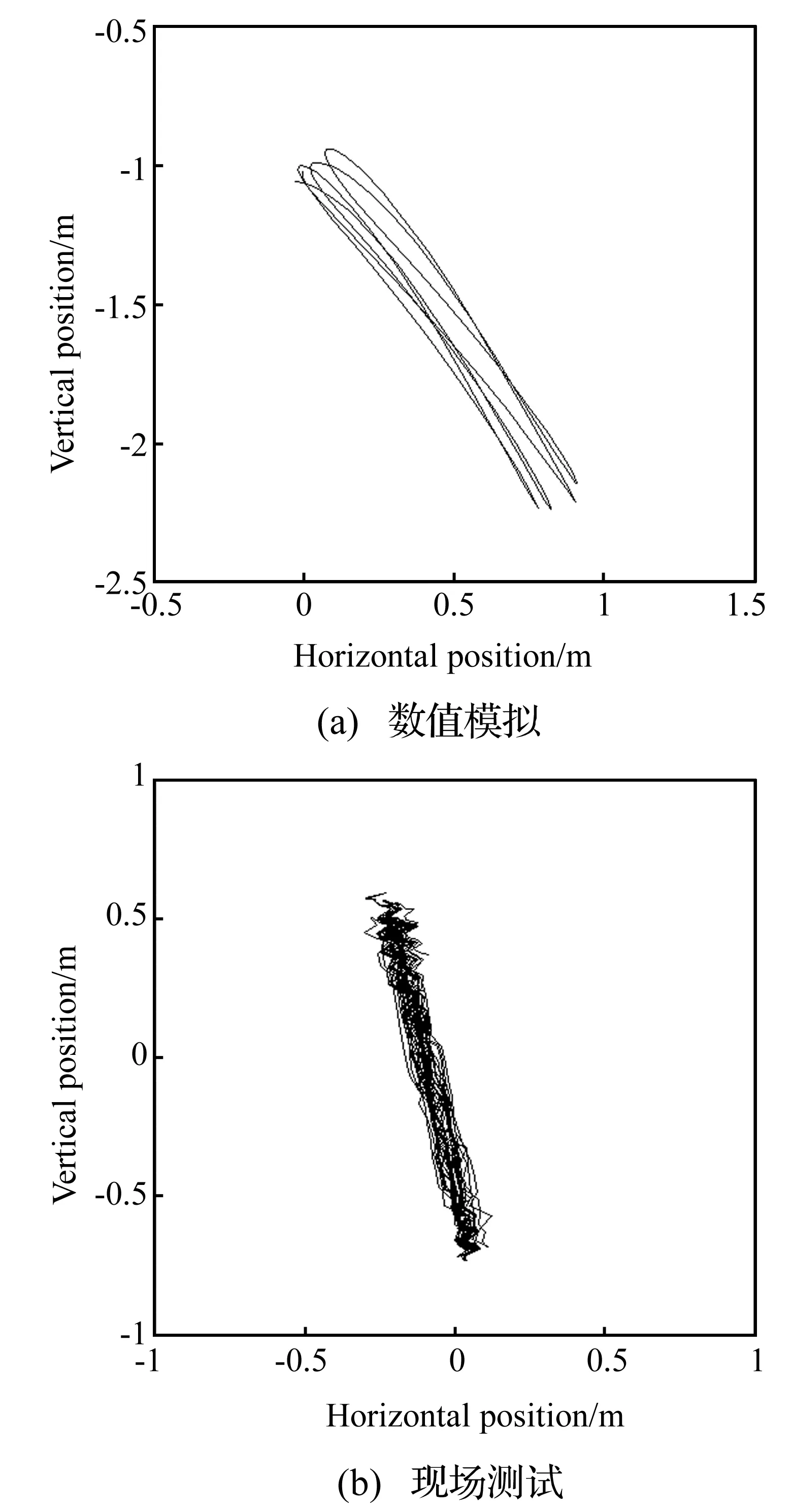
图7 第3档中相子导线1靠近3号塔第一个间隔棒处的舞动轨迹

图8 迎风相导线不同位置的舞动轨迹

3.2 舞动响应谱分析

舞动过程中的振动形态和频率是极为重要的特征。为此，首先利用有限元模型，计算得到塔线体系的固有频率和模态，得到的第3档安装了D形覆冰模型的六分裂导线中相在垂直、水平、扭转三个方向上的前3阶固有频率和模态如表2所列。

表2 安装D形覆冰模型六分裂导线固有频率和模态

图9所示为由数值模拟和实测得到的实测点的位移响应谱。由图9(a)可知，数值模拟得到的导线舞动垂直运动的主频接近于垂直一阶频率，即导线在垂直方向的振动以双半波模态为主。另外，在三半波对应的固有频率附近也有一个小的峰值。图9(b)所示的导线水平运动的频谱可见，除了对应于垂直方向的振动频率外，在低频区域有响应，这是随机风速的低频分量作用下的受迫振动响应。图9(c)和(d)为实测响应的频谱，可见峰值频率与数值模拟的结果一致。表明数值模拟正确反映了试验线路舞动的形态和频率特征。

3.3 舞动过程中导线张力

现场试验第3档与3号杆塔连接的中相导线耐张绝缘子串处，安装了张力传感器测试六分裂导线的张力。表3所列为数值模拟和实测的导线中的静态张力和舞动过程中导线张力变化的范围。从表中可看出，数值模拟与现场记录的导线的静态张力相对误差仅为1.19%；而导线舞动过程中的张力变化范围也较接近。

图9 实测点处导线的位移响应频谱

现场记录与数值模拟得到的导线舞动过程中动态张力与静态张力比值随时间的变化如图10所示，可见两者接近。

表3 现场记录与数值模拟的导线张力

图10 动态张力与静态张力比值随时间变化曲线

4 结 论

本文建立了真型试验线路塔线耦合体系有限元模型，对安装D形覆冰模型的六分裂导线进行了舞动数值模拟，并与现场实测结果进行了比较分析。得到如下结论：

(1)数值模拟得到的六分裂导线的舞动轨迹和实测结果基本一致；

(2)数值模拟得到的舞动形态和频率与实测结果一致；

(3)数值模拟得到的导线静态张力以及舞动过程中的张力变化与实测结果一致；

(4)基于数值模拟结果和实测结果的一致性，验证了数值模型和数值模型方法的正确性；

(5)数值模型和模拟方法可以进一步用于舞动特征和防舞技术研究，为现场试验方案的制定提供指导。

[1]Gurung C B，Yamaguchi H，Yukino T.Identification of large amplitude wind-induced vibration of ice-accreted transmission lines based on field observed data[J].Engineering Structure，2002，24: 179-188.

[2]Gurung C B，Yamaguchi H，Yukino T.Identification and characterization of galloping of Tsuruga test line based on multi-channel modal analysis of field data[J].Journal of Wind Engineering and Industrial Aerodynamics，2003，91: 903-924.

[3]Dyke P V，Laneville A.Galloping of a single conductor covered with a D-section on a high-voltage overhead test line[J].Journal of Wind Engineering and Industrial Aerodynamics，2008，96:1141-1151.

[4]Desai Y M，Yu P，Popplewell N，et al.Finite element modeling of transmission line galloping[J].Computers & Structures，1995,57(3)：407-420

[5]Zhang Q，Popplewell N，Shah H.Galloping of bundle conductor [J].Sound and Vibration，2000,234(1):115-134.

[6]Liu X H，Yan B，Zhang H Y，et al，Nonlinear numerical simulation method for galloping of iced conductor [J].Applied Mathematics and Mechanics-English Edition，2009，30(4): 489-500.

[7]Hu J，Yan B，Zhou S，et al.Numerical investigation on galloping of iced quad bundle conductors [J].IEEE Transactions on Power Delivery，2012，27(2): 784-792.

[8]Baenziger M A，James W D，Wouters B，et al.Dynamic loads on transmission line structures due to galloping conductors[J].IEEE Transactions on Power Delivery，1994，9(1): 40-46.

[9]李黎，曹化锦，罗先国，等.输电塔-线体系的舞动及风振控制[J].高电压技术，2011，37(5)：1253-1260.

LI Li，CAO Hua-jin，LUO Xian-guo，et al.Galloping and wind-induced vibration control on transmission tower-line system[J].High Voltage Engineering，2011，37(5)：1253-1260.

[10]曹化锦，李黎，姜维，等.输电塔-线体系舞动仿真及控制研究[J].振动与冲击，2011，30(12)：245-249.

CAO Hua-jin，LI Li，JIANG Wei，et al.Simulation and control for galloping of a transmission tower-line system[J].Journal of Vibration and Shock，2011,30(12)：245-249.

[11]赵莉，严波，蔡萌琦，等.输电塔线体系中覆冰导线舞动数值模拟研究[J].振动与冲击，2013,32(18):113-120.

ZHAO Li，YAN Bo，CAI Meng-qi，et al.Numerical simulation for galloping of iced conduciors in a transmission tower-line system[J].Journal of Vibration and Shock，2013,32(18):113-120.

[12]Yan B，Lin X S，Luo W，et al.Numerical study on dynamic swing of suspension insulation in overhead transmission line under wind load [J].IEEE Transactions on Power Delivery，2010，25(1): 248-259.

[13]国家电力公司东北电力设计院.电力工程高压送电线路设计手册[M].第二版，北京：中国电力出版社，2003.

[14]GB50135-2006.高耸结构设计规范[S].第一版，北京：中国计划出版社，2007.

[15]张相庭.结构风工程[M].北京：中国建筑工业出版社，2006.