辊环外圆磨床砂轮主轴的转子动力学分析
2014-09-04陈晓枫
钱 梅 陈晓枫
辊环外圆磨床砂轮主轴的转子动力学分析
钱 梅 陈晓枫
(上海机床厂有限公司 上海200093)
利用ANSYS建立了两种砂轮主轴的有限元模型,分别对其进行了转子动力学模态分析,得到了坎贝尔图并对结果进行了对比分析。分析结果表明,通过改变影响临界转速的参数、轴的几何参数和轴承的刚性等,使主轴系统的性能达到了预期的设计要求,同时证明,砂轮主轴所使用的圆锥滚子轴承对最高转速的限制,成为砂轮主轴系统转速不能更大幅度提高的根本原因。
砂轮主轴 转子动力学 临界转速 坎贝尔图
随着旋转机械性能的不断提高,转子系统朝着高转速、高效率的方向发展。转速的提高使得转子与轴承间的作用力不断增强,会导致振动过载和振动位移增大。同时由于转子不平衡造成的离心力使转子产生横向振动,这种振动在某些转速(临界转速)附近会因为共振而显得异常强烈。合理配置转子支承系统是保证旋转机械安全可靠运行的一项重要前提,因此对高速旋转系统进行转子动力学分析是很重要而且也很必要[1]。
砂轮主轴系统是辊环外圆磨床的关键部件,其性能的好坏直接影响着工件的加工精度。国内现有的砂轮主轴系统结构形式的最高转速仅为1 910 r/min,而德国砂轮主轴系统的结构形式的最高转速为8 000 r/min。利用ANSYS对这两种砂轮主轴系统进行了建模和动力学分析,得到了频率、振型和临界转速,对两种主轴系统进行了对比,并且对影响临界转速的因素进行了分析,改进了国内主轴系统结构形式。
1 有限元模型的简化和建立
砂轮主轴系统主要由砂轮、主轴、皮带轮和2个支承轴承组成,砂轮和皮带轮位于主轴的两端,电动机通过皮带轮将动力传递给主轴,从而带动主轴高速旋转,如图1、图2所示。

图1 国内砂轮主轴示意图
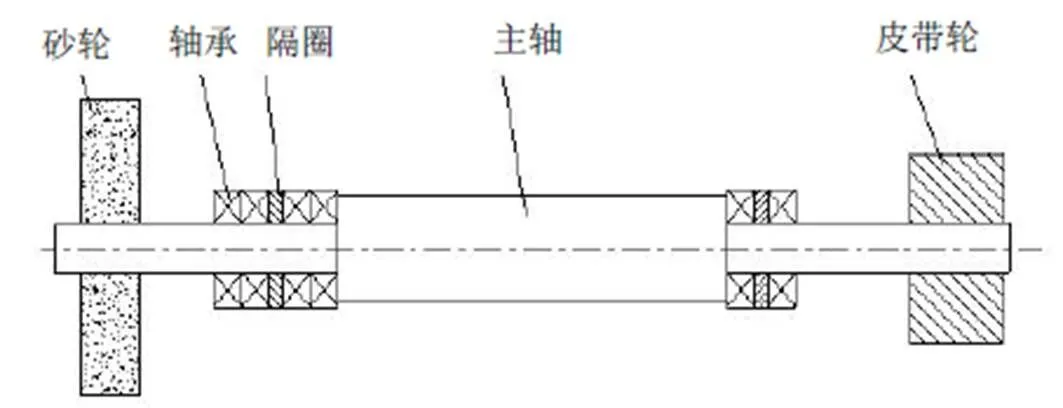
图2 国外砂轮主轴示意图
将砂轮和皮带轮简化为2个质量圆盘,2个支承轴承简化为弹簧阻尼,因此在转轴高速旋转时,2个圆盘的中心会偏离转轴中心1、2,产生两个偏心力,从而引起转轴的不平衡,产生振动。由于砂轮和皮带轮在转轴的两端,因此在转动时圆盘会给转轴施加一个力矩,即陀螺力矩:=pΩnsin,p为极转动惯量,为圆盘轴线与轴承支点连线的夹角。当0<</2(正进运动)时,陀螺力矩使转轴变形量减小,增大转轴的弹性刚度,从而提高转子的临界转速;当/2<<(反进运动)时,转轴变形量增大,转轴刚度减小,因此也降低了转子的临界转速。由上所述,可得到此模型的转子动力学模型[2]:

式(1)中,为各质量块位移列阵;为质量矩阵;为陀螺力矩矩阵;Ω为转子的转动角速度;为阻尼矩阵;为刚度矩阵;为偏心力的初始相位;1、2为偏心距。
2 国内和国外砂轮主轴系统的结构参数对比[3]
国内砂轮主轴系统的结构参数如下:
1)几何参数(砂轮主轴的截面直径和长度)
1=0.027 m2=0.06 m3=0.068 m4=0.08 m5=0.083 m6=0.1 m7=0.11 m8=0.075 m9=0.065 m10=0.064 m11=0.06 m12=0.036 m1=0.034 m2=0.0565 m3=0.106 m4=0.123 m5=0.139 m6=0.155 m7=0.18 m8=0.2 m9=0.52 m10=0.56 m11=0.5715 m12=0.6145 m13=0.624 m14=0.639 m15=0.698 m16=0.728 m17=0.78 m
2)其他物理参数(圆盘的质量、转动惯量和轴承的径向刚度)
1=15 kgJ1=0.117 2 kg·m2JD1=0.058 6 kg·m2K1=1.85×109N/mK1=1.85×109N/m
2=8 kgJ2=0.013 kg·m2J2=0.006 5 kg·m2K2=1.680 6×109N/mK2=1.680 6×109N/m
国外砂轮主轴系统的结构参数如下:
1)几何参数
1=0.042 m2=0.09 m3=0.15 m1=0.015 m2=0.062 m3=0.147 m4=0.171 m5=0.204 m6=0.228 m7=0.240 m8=0.570 m9=0.582 m10=0.618 m11=0.722 5 m12=0.765 m13=0.780 m
2)其他物理参数
1=15 kgJ1=0.117 2 kg·m2J1=0.058 6 kg·m2K1=2.17×109N/mK1=2.17×109N/m
2=7 kgJ2=0.013 kg·m2J2=0.006 5 kg·m2K2=6.372×108N/mK2=6.372×108N/m
国内和国外砂轮主轴系统的主轴有限元模型如图3所示。

(a)国内砂轮主轴系统主轴的有限元模型 (b)国外砂轮主轴系统主轴的有限模型
3 分析结果
国内的砂轮主轴系统结构分析结果如下:
坎贝尔图(如图4所示)。

图4 国内主轴系统坎贝尔图
从图4可以得到:一阶转速为6 750 r/min,二阶转速为6 845 r/min,三阶转速为55 840 r/min,四阶转速为61 200 r/min。
四阶振型图(如图5所示)。

图5 国内主轴振型图
国外的砂轮主轴系统结构分析结果如下:
坎贝尔图(如图6所示)。

图6 国外主轴系统坎贝尔图
从图6中可以得到:一阶转速为31 643 r/min,二阶转速为44 751 r/min,三阶转速为45 773 r/min,四阶转速为49 414 r/min。
四阶振型图(如图7所示)。

图7 国外砂轮主轴振型图
通过以上对国内和国外的砂轮主轴进行转子动力学的有限元分析比较得到,国内的砂轮主轴一阶、二阶转速较低,三、四阶变化较大;而国外的砂轮主轴四阶转速都是呈均匀变化,且设计要求国内正常工作时的转速在6 000~8 000 r/min,恰好在其共振区域内,因此需要修改影响其临阶转速的参数,以达到设计结构的性能要求。
4 砂轮主轴的优化
1)优化理论和方法
影响临界转速的主要参数有轴段的抗弯刚度、轴段的长度、圆盘的质量和支撑的刚性等,某一阶临界转速可能对系统某些参数变化是敏感的,而另一些是不敏感的,因此可以通过改变敏感的参数调整临界转速,从而达到优化转子系统性能的目的。
设在某一转子系统中,有阶临界转速需要改变,其改变量为:

现有个参数p=(1,2,…,)允许作适当的调整,设参数的修改量为:
可得:(2)
当=时,对由非奇异Jacobi矩阵,由式(1)可得各参数的调整量﹛△﹜,系统调整后的参数:
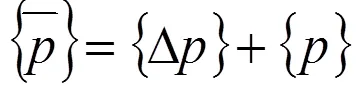
式(3)中,﹛﹜为调整前的参数矩阵。当>时,式(2)是超定方程,在一般情况下无解。但可用最小二乘法即在全部方程误差平方和为极小值的意义的情况下求解。可令误差向量为﹛﹜,即:
(4)
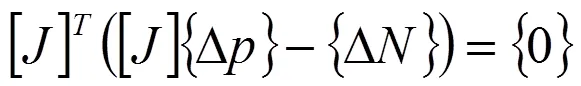
由式(5)可得:
(6)
在实际问题中,较多的是<,这时式(2)是一组亚定方程,有无穷多组解。因此可以用最优化方法求解,选﹛△﹜平方和为基本目标函数,则整个目标函数为:
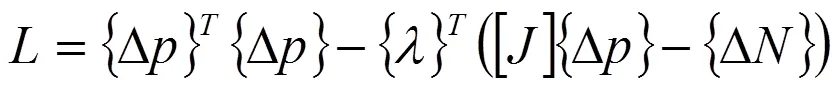
(8)
有极小值,可求得:

由于所工作的工况不变,可以通过改变砂轮主轴的几何结构和轴承的刚度来优化临界转速。
修改后的参数如下:
1)几何参数
1=0.03 m2=0.06 m3=0.085 m4=0.1 m5=0.103 25 m6=0.115 m7=0.12 m8=0.102 m9=0.09 m10=0.085 m11=0.08 m12=0.048 m
1=0.034 m2=0.056 5 m3=0.105 m4=0.128 m5=0.146 5 m6=0.165 m7=0.183 m8=0.215 m9=0.536 m10=0.586 m11=0.598 m12=0.657 m13=0.667 m14=0.688 m15=0.762 m16=0.802 m17=0.868 m
2)其他物理参数
1=15 kgJ1=0.117 2 kg·m2J1=0.058 6 kg·m2K1=2.17×109N/mK1=2.17×109N/m
2=7 kgJ2=0.013 kg·m2J2=0.006 5 kg·m2K2=6.372×108N/mK2=6.372×108N/m
修改砂轮主轴参数后的分析结果如下:
坎贝尔图(如图8所示)。

图8 修改后的国内砂轮主轴坎贝尔图
四阶振型图(如图9所示)。

图9 修改后国内主轴振型图
从图8中可以得到:砂轮主轴的一阶转速为26 751 r/min,二阶转速为33 439 r/min,三阶转速为35 350 r/min,四阶转速为40 127 r/min。
从优化后的分析结果可知:一阶临界转速有了大幅度的提高且四阶转速变化均匀。由于主轴所使用的是圆锥滚子轴承,虽然其承载力较大,但是转速不高,因此限制了主轴转速的大幅度提高。
5 结语
针对国内和国外两种砂轮主轴结构系统,利用ANSYS进行了转子动力学的分析,并对结果进行了对比,根据优化理论和方法,通过改变砂轮主轴的几何结构和轴承的刚度,可以大幅度地提高一阶临界转速,使四阶转速变化均匀。由于砂轮主轴使用的是圆锥磙子轴承,承载力虽然较大,但转速不高,从而限制了砂轮主轴转速的大幅度提高,因此建议在结构允许的情况下选用滚珠轴承。
[1] 孟光.转子动力学研究的回顾与展望[J].振动工程学报,2002,15(1):1-9.
[2] 钟一锷,何衍宗,王正,等.转子动力学[M].清华大学出版社,1989.
[3] 曾攀,雷丽萍,方刚.基于ANSYS平台有限元分析手册[M].北京:机械工业出版社,2011.
