运用速度-时间图像对追及问题与传送带问题进行类比分析

(南京师范大学附属中学高二14班，江苏 南京 210003)

在高中力学的学习中，传送带问题是一类比较经典的题型.这类题型大多物理情景模糊，条件隐蔽、过程复杂，也因此成为不少学生困惑的难点.而追及问题的物理图像较为清晰，本文首先应用v-t图像分析追及问题，然后将追及问题与传送带问题进行类比，并以v-t图像为纽带在二者之间寻找联系，抓住图像解题过程中的一些要点，从而分析两者共通的解题思路，降低此类题型的解题难度.

1 运用v-t图像求解追及问题

v-t图像表达了物体运动的速度随时间的变化规律.速度图线斜率的大小等于加速度的大小.下面以两个均作匀加速直线运动的物体为例，浅析一下v-t图像求解两物体追及问题时的几个要点.

例1 甲、乙两物体同时同向作匀加速直线运动，一开始甲在后，乙在前，两者相距x0.甲的初速度为v1，加速度为a1；乙的初速度为v2(v1>v2)，加速度为a2，问两物体是否会相遇？

我们可以作出两物体的v-t图像，它们与v轴交点的纵坐标代表两物体的初速度v1和v2，速度图像与t轴围成的“面积”表示物体在Δt时间内的位移，那么甲乙的位移之差的大小就是两者与t轴围成的“面积”之差，即Δs.而两者的距离L则是两者的初始距离x0减去两物体的位移差，即L=x0-Δs.对于这道题，我们可以根据甲和乙的加速度对比，分两种情况讨论.

图1

(1)当甲的加速度大于等于乙时，即a1≥a2，甲、乙两物体的v-t图像如图1所示.随着时间t的增加，两物体的v-t图线与t轴围成的“面积”之差Δs会不断变大.由L=x0-Δs可知，当x0=Δs时，甲会追上乙.

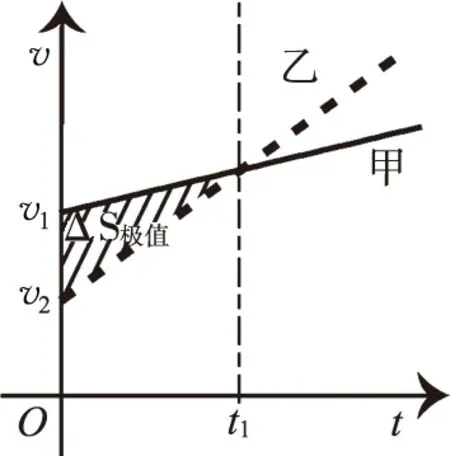
图2

(2)当甲的加速度小于乙时，即a1x0时，由L=x0-Δs可知，L=0的情况会出现两次，那么甲不仅可以追及上乙一次，之后甲又会被乙反追上一次，即两者可以相遇两次.而当Δs极值=x0时，甲只能追及上乙一次.如果Δs极值

我们发现两条v-t图线的交点时刻(不一定会有)以及此时的位移差大小Δs极值往往是解题的关键.我们不妨来关注它们，在交点位置时两者速度相等，位移差Δs就出现了一个极值，这个极值往往决定了两物体能否相遇.因此，t1时刻及0-t1时间内速度图线与围成的“面积”Δs极值是解决追及问题的关键.

2 运用v-t图像求解传送带问题

在高中力学各类题型中，传送带问题的难度一直比较大，但传送带问题在运用图像法解题时，可以发现其v-t图像与追及问题有类似之处，因此可以尝试将两者进行类比分析.作两条v-t图线，一条代表传送带上物体的速度，另一条代表传送带的速度.我们将传送带看做是追及问题的一个对象，问题就变成了物体“追”传送带的问题，下面以例2说明这种思路.

图3

例2 如图3所示，一条长为l的传送带沿逆时针以v的速度匀速运动.一个不计长度的小木块以v0(v0

图4

对于这道题，我们可以作木块和传送带的v-t图像.如图4所示，实线代表木块的运动速度随时间的变化；水平虚线表示的是传送带的匀速直线运动.图4中t1时刻代表木块的速度与传送带的速度相等的时刻.以t1为分界，我们把该图像分为Ⅰ、Ⅱ两个阶段.在阶段Ⅰ中，木块初速度为v0，因为v0

(1)当gsinθ>μgcosθ时，物体具有加速度a2=gsinθ-μgcosθ>0，这个加速度大小就是图4中阶段Ⅱ中图线①的斜率.

(2)当gsinθ≤μgcosθ时，这种情况下摩擦力的为静摩擦力，与重力沿传送带方向的分力相平衡.小木块和传送带保持相对静止，处于匀速直线运动状态.此时加速度a2=0，v-t图像如图4中阶段Ⅱ中图线②所示.

分析清楚木块运动的v-t图线之后，木块运动的距离s可以由v-t图像与t轴围成的“面积”表示，求解s=l时t的大小，就可以解决这道题了.

3 小 结

追及问题和传送带问题在运用v-t图像求解时，有类似之处，也有不同之处.类似之处在于两条v-t图线的交点，即两物体速度相等的时刻往往都是解题的关键.在追及问题中，这一点代表两者的位移差出现极值；而在传送带问题中，达到相同的速度的时刻是摩擦力突变之时，而摩擦力的突变带来了加速度的突变.

(指导教师：南京师范大学附属中学 陈 明)

参考文献：

[1]黄才发.传送带问题中的一题变式[J].物理教学探讨,2013,(3):37.

[2]李越，樊晓东.运用速度时间图像求解追及、相遇问题[J].物理教学探讨,2013,(3):12.

[3]许红，王兴林.巧用v-t图像妙解物理难题[J].科教文汇,2007,(7):64.

[4]人民教育出版社，课程教材研究所，物理课程教材研究开发中心．普通高中课程标准实验教科书 物理必修1[M]．北京：人民教育出版社，2010．