物体在传送带上的运动剖析

孙建中

（句容市第三中学 江苏 镇江 212400）

传送带在工农业生产中有着广泛的应用．近年来与传送带有关的内容成为高考的热点，在各地高考中也出现很多．物体在传送带上运动问题的分析几乎涉及力学的全部知识，如匀变速运动、牛顿运动定律、能量守恒以及功能关系等．本文就物体在传送带上的运动问题逐一展开论述．

1 传送带水平放置

设两定滑轮之间的距离为L，物体与传送带之间的动摩擦因数为μ，物体m置于传送带一端，初速度为v0，传送带的速度为v带．

情形一：v0＝0，如图1所示．

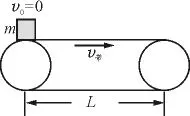
图1

物体刚置于传送带上时，由于受滑动摩擦力作用，将做a＝μg的匀加速直线运动．假定物体一直匀加速运动到离开传送带右端，则其离开传送带时的速度，显然：

情形二：v0≠0，且v0与v带同向，如图2所示．

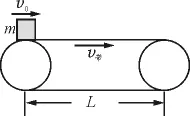
图2

（1）当v0＜v带时

同上可知，物体刚运动到带上时，将做a＝μg的匀加速直线运动，假定物体一直匀加速到离开传送带右端，则其离开传送带时的速度v＝，显然：

（2）当v0＝v带时

物体将一直随传送带一起做匀速直线运动直至从传送带的右端离开．

（3）当v0＞v带时

物体刚运动到传送带时，因v0＞v带，将做a＝μg的匀减速直线运动，假定物体一直匀减速运动到离开传送带，则其离开传送带时的速度v＝，显然：，物体在传送带上将一直匀减速运动直至从传送带的右端离开．

情形三：v0≠0，且v0与v带反向，如图3所示．

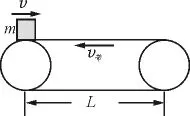
图3

此种情形下，物体刚运动到传送带上时将做a＝μg的匀减速直线运动，假定物体一直匀减速到离开传送带的右端，则其离开传送带时的速度，显然：

（1）若0＜v0≤v带，物体将先沿v0方向做匀减速直线运动到速度为零，而后反向一直匀加速直线运动，直至从放入端离开传送带．

（2）若v0＞v带，物体将先沿v0方向做匀减速直线运动到速度为零，而后反向匀加速直线运动到速度等于传送带速度，最后随传送带一起匀速运动直至从放入端离开传送带．

2 传送带斜置 物体置于传送带下端

设传送带两定滑轮间的距离为L，传送带与水平面的夹角为θ，物体与传送带之间的动摩擦因数为μ，物体m置于传送带的下端，初速度为v0，传送带的速度为v带．

情形一：v0＝0，如图4所示．

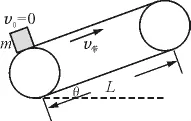
图4

物体放到传送带的下端时，因v0＝0，显然只有μmg cosθ－mg sinθ＞0，即μ＞tanθ时，物体才会随传送带从下向上做a＝μg cosθ－g sinθ的匀加速直线运动，假定物体一直匀加速运动到传送带上端，则物体在离开传送带时的速度

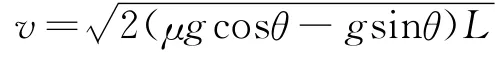
显然：

情形二：v0≠0，且v0与v带同向，如图5所示．

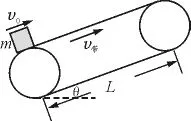
图5

（1）v0＜v带时

1）若μ＞tanθ，物体刚运动到带上时，因v0＜v带，则其将沿传送带向上做a＝μg cosθ－g sinθ的匀加速直线运动，假定物体一直做匀加速运动，则物体离开传送带上端时的速度为

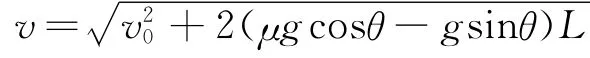
显然：

2）若μ＝tanθ，物体将以v0沿传送带一直做匀速直线运动直至从传送带的上端离开．

3）若μ＜tanθ，物体刚运动到带上时，因v0＜v带，故物体将沿传送带向上做a＝g sinθ－μg cosθ的匀减速直线运动．假定物体一直做匀减速运动直至离开传送带，则物体离开传送带上端时速度为

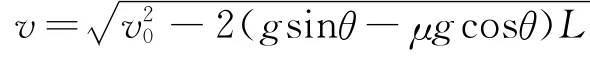
显然：

（2）v0＞v带时

1）若μ＞tanθ，物体刚运动到传送带上时，因v0＞v带，故物体将沿传送带向上做a＝g sinθ＋μg cosθ的匀减速直线运动，假定物体一直做匀减速运动直至离开传送带上端，则物体离开传送带时速度为

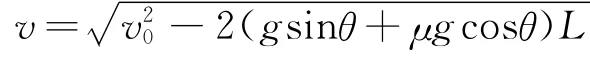
显然：

2）若μ＝tanθ，物体将以v0沿传送带一直做匀速直线运动直至从传送带的上端离开．

3）若μ＜tanθ，物体刚运动到带上时，因v0＞v带，故物体将沿传送带向上做a＝g sinθ＋μg cosθ的匀减速直线运动．假定物体一直做匀减速运动直至离开传送带，则物体离开传送带上端时速度为

显然：

1）先向上做a＝g sinθ＋μg cosθ的匀减速运动到速度等于传送带速度，而后向上做a＝g sinθμg cosθ的匀减速运动，直至离开传送带上端．

2）先向上做a＝g sinθ＋μg cosθ的匀减速运动到等于传送带速度，而后向上做a＝g sinθ－μg cosθ的匀减速运动到速度为零，最后反向做a＝g sinθμg cosθ的匀加速运动直至从传送带下端离开．

情形三：v0≠0，且v0与v带反向，如图6所示．

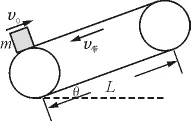
图6

物体刚运动到传送带下端时，物体将做a＝g sinθ＋μg cosθ的匀减速直线运动，假定物体一直做匀减速运动直至离开传送带上端，则其离开上端时速度为显然：

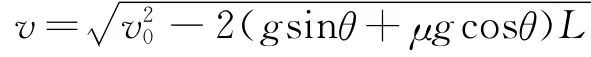
（1）当μ＞tanθ时，物体将先沿传送带向上做匀减速运动到速度为零，而后向下做a＝g sinθ＋μg cosθ的匀加速运动到速度等于传送带速度，最后随传送带一起做匀速运动直至从传送带下端离开．

（2）当μ＜tanθ时，物体将先沿传送带向上做匀减速运动到速度为零，而后向下做a＝g sinθ＋μg cosθ的匀加速运动到速度等于传送带速度，最后沿传送带向下做a＝g sinθ－μg cosθ的匀加速运动直至从传送带下端离开．

3 传送带斜置 物体置于传送带上端

设传送带两定滑轮间的距离为L，传送带与水平面的夹角为θ，物体与传送带之间的动摩擦因数为μ，物体m置与传送带的上端，初速度为v0，传送带的速度为v带．

情形一：v0＝0，v带向上，如图7所示．

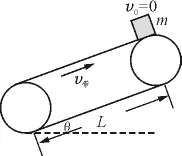
图7

物体刚放到传送带的上端时，因v0＝0，显然只有mg sinθ－μmg cosθ＞0，即μ＜tanθ时，物体才能沿传送带从上往下做a＝g sinθ－μg cosθ的匀加速直线运动，且物体将一直匀加速运动到传送带下端，物体离开传送带时的速度为

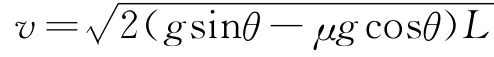
情形二：v0≠0，且v0与v带反向，如图8所示．

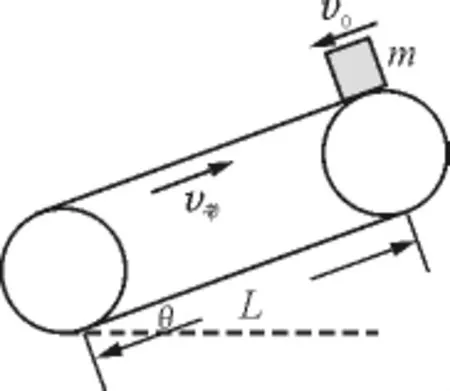
图8

（1）若μ＜tanθ时，物体将一直沿传送带做匀加速直线运动到传送带下端离开传送带．物体离开传送带时的速度为v＝

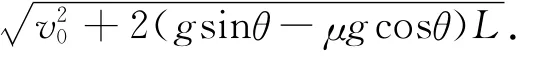
（2）若μ＞tanθ时，物体刚运动到传送带上后将沿传送带从上往下做a＝μg cosθ－g sinθ的匀减速直线运动，假定物体一直匀减速到下端，则物体离开传送带时的速度为

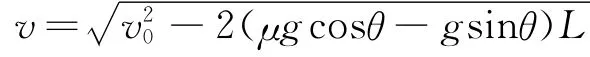
显然：

1）若v0≤v带，物体将一直做匀加速运动直至从传送带上端离开．

2）若v0＞v带，物体将先匀加速运动到速度等于传送带速度，而后随传送带一起匀速运动直至从传送带上端离开．

情形三：v0＝0，v带向下，如图9所示．

图9

物体刚放到带的下端时，因v0＝0，物体在传送带带动下，从上而向下做a＝g sinθ＋μg cosθ的匀加速直线运动，假定物体一直匀加速运动到传送带的下端，则物体在离开传送带时的速度为

显然：

1）若μ＜tanθ，物体将继续做a＝g sinθμg cosθ的匀加速运动从传送带下端离开．

2）若μ＞tanθ，物体将随传送带一起匀速运动直至从传送带下端离开．

情形四：v0≠0，v带向下，如图10所示．

图10

（1）v0＜v带时

1）若μ＞tanθ，物体刚运动到带上时，因v0＜v带，则其将做a＝μg cosθ＋g sinθ的匀加速直线运动，假定物体一直做匀加速运动，物体离开传送带下端时的速度为

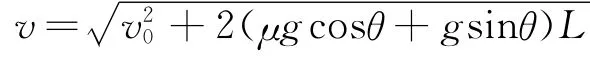
显然：

2）若μ＜tanθ物体刚运动到传送带上时，因v0＜v带，物体将做a＝g sinθ＋μg cosθ的匀加速直线运动．假定物体一直做匀加速运动直至离开传送带，则物体离开传送带上端时速度为

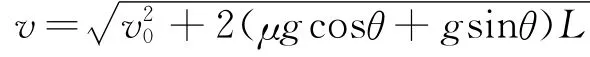
显然：

（2）v0＞v带时

1）若μ＞tanθ，物体刚运动到带上时，因v0＞v带，故物体将做a＝μg cosθ－g sinθ的匀减速直线运动，假定物体一直做匀减速运动，则物体离开传送带下端时速度为

显然：

2）若μ＜tanθ，物体刚运动到带上时，因v0＞v带，故物体将一直做a＝g sinθ－μg cosθ的匀加速直线运动．运动到离开传送带下端时速度为

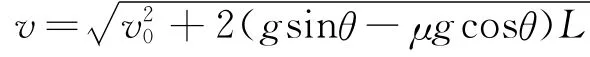
上面依据牛顿运动定律、匀变速运动规律对物体在传送带上的运动特征进行了分析，实际上还可根据能量观点对其进行分析，限于篇幅，本文在这里不再赘述．