大姿态角入水时的鱼雷半实物仿真方法研究

郝 喆，张秦南，王立文，王 中

(1.中国船舶重工集团公司第705研究所，陕西 西安 710075;2.水下信息与控制重点实验室，陕西 西安 710075)

0 引言

根据实航试验结果统计，空投鱼雷的入水姿态范围为:航向角:－180°～180°;滚动角: －180°～180°;俯仰角: －30°～ －85°。

采用立式三轴转台进行控制系统仿真时，当俯仰角大于－70°情况下，控制系统半实物仿真中会出现发散，导致仿真试验失败，或产生强烈的运动学耦合，与数学仿真结果差异较大，而且转台的输入值与输出值不吻合，试验结果不可信。

通过重新定义欧拉角以及合理设置转台的角速率限幅值和角加速度限幅值可以解决上述问题。本文对大姿态角入水下的半实物仿真问题进行深入分析，针对立式三轴转台提出基于正欧拉角或反欧拉角的半实物仿真方法，试验结果表明仿真方法有效可行，而采用正欧拉角还是反欧拉角，可以事先通过数学仿真进行确定。

1 问题分析和解决方法

1.1 欧拉角定义

绕定点转动的刚体相对参考坐标系的角位置，可以用3次独立转动的3个转角来确定。这就是著名的欧拉法。这3个独立的角度称为欧拉角。在实际使用中欧拉角的选取不唯一，要视具体情况而定［1］。

当选取发射点地理坐标系作为参考坐标系时，通常按航向角ψ、俯仰角θ、滚动角γ的顺序旋转可以得到雷体坐标系。按这样顺序定义欧拉角时，航向角ψ的定义为雷体ox1在水平面的投影与地面坐标系ox轴的夹角，俯仰角定义为导弹纵轴ox1与水平面的夹角，滚动角γ定义为雷体oy1轴与过ox1轴的铅垂面的夹角。当鱼雷处于垂直状态时，即俯仰角θ为90°时，ox1轴在水平面的投影为1个点，使航向角无意义;过ox1轴的铅垂面有无穷多个，使滚动角无意义。为了避免俯仰角为90°时滚动角和航向角无意义，需要重新定义1套欧拉角。

参考坐标系 (如发射点地理坐标系)按航向角、滚动角、俯仰角的顺序旋转也可以得到雷体坐标系。航向角定义为雷体坐标系oz1轴在水平面的投影与参考坐标系oz轴的夹角，滚动角定义为雷体坐标系oz1轴与水平面的夹角，俯仰角定义为垂直于oz1轴的平面和水平面的交线与雷体坐标系ox1轴的夹角。由此可见，上述2种欧拉角的定义不同。按航向角、滚动角、俯仰角的顺序旋转定义的欧拉角计为ψ1(航向角)、γ1(滚动角)、θ1(俯仰角)。

1.2 转台限幅特性分析

转台用于跟踪仿真计算机解算出的欧拉角，当仿真中解算出的角速率和角加速度大于设定的转台限幅值就会出现失真，即转台的输出欧拉角与解算不一致，其实质是仿真应遵循的相似性原理得不到满足［4－6］。

为了对转台限幅特性进行研究和对控制系统发散进行定量分析，在仿真计算机中人为加入幅值为20°、频率为1 Hz的正弦信号驱动转台的滚动框，控制系统跟踪转台信号，仿真结果如图1所示。转台角加速度限幅为500°/s2时转台输出有延迟和幅值衰减，转台角加速度限幅为800°/s2时转台输出无延迟和衰减。角速度限幅情况与上述结果类似。

发散原因定位为转台3个框的角加速度限幅值低于相应计算值。

图1 不同角加速度限幅下转台滚动框输出与敏感元件测量曲线 (转台滚动框输入为幅值为20°、频率为1 Hz的正弦信号)Fig.1 On the different angle acceleration limiting amplitudc the output of the turn-table roll frame and the measurement curves of sense organ(the input of turn-table roll frame is 20°，frequency is 1 Hz of sine signal)

1.3 正欧拉角方程和分析

欧拉角ψ，θ和γ随时间的变化规律为:

由式(1)可知，当俯仰角接近－90°时，欧拉角的变化率接近无穷大，而在－90o时方程出现奇异无法求解。由式(1)及其微分可以估算转台3个框的角速度和角加速度的最大值。

利用式(1)进行仿真时，解算出的欧拉角ψ，θ和γ分别驱动转台的外框、中框、内框，而转台每个框的角速率和角加速度一般要进行限幅，解算出的角速率和角加速度大于设定的转台限幅值就会出现失真，即转台的输出欧拉角与解算不一致，其实质是仿真应遵循的相似性原理得不到满足。

1.4 反欧拉角方程和分析

反欧拉角 ψ1，θ1和 γ1随时间的变化规律为［2］:

由式(2)及微分可以估算转台3个框的角速度和角加速度的最大值。当数学仿真中滚动角γ1小于45o时，则可以进行控制系统半实物仿真，相应欧拉角的角速率可以满足转台每个框的角速率和角加速度的限幅值。当数学仿真时若滚动角γ1接近90°时，也需要重新定义欧拉角。

2 仿真结果

假定正欧拉角ψ，θ和γ的初值为0°，－75°和150°，则反欧拉角 ψ1，γ1和 θ1的初值依次为－150.86°，7.44°和 －103.07°。利用数学仿真进行计算，可以估算试验中转台3个框所需的角速度和角加速度。角速度和角加速度最大计算值 (见表1)。

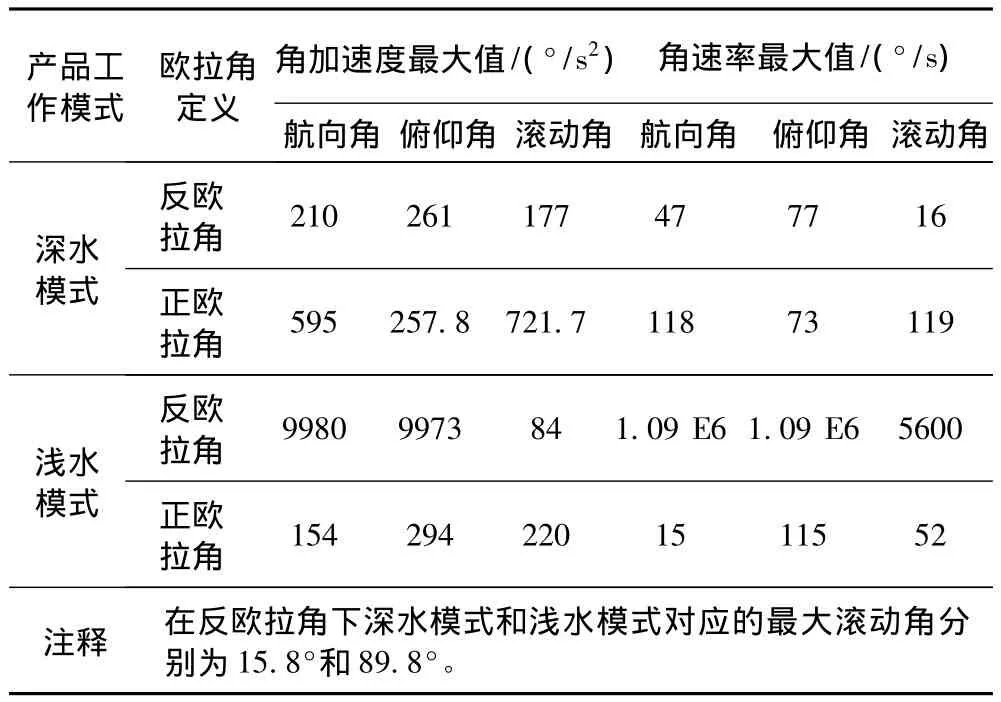
表1 角速度和角加速度最大计算值Tab.1 The max angle rate and angle acceleration

由表1可知，产品工作于深水模式时采用反欧拉角易于进行半实物仿真;产品工作于浅水模式时采用正欧拉角可以进行半实物仿真，而采用反欧拉角时，由于转台不能实现相应的最大角速度和角加速度，因而无法进行半实物仿真。

图2为深水工作模式下控制系统半实物仿真曲线 (采用反欧拉角)。

图3为浅水工作模式下控制系统半实物仿真曲线 (采用正欧拉角)。

试验表明，半实物仿真结果与数学仿真结果吻合，说明半实物仿真结果可信，控制系统半实物仿真试验有效，同时表明仿真方法可行。

3 结语

本文通过合理定义欧拉角及设置转台的角速率限幅值和角加速度限幅值可以实现大姿态控制系统的半实物仿真。通过仿真计算和试验结果分析主要结论如下:

图2 深水工作模式下控制系统半实物仿真曲线(采用反欧拉角)Fig.2 The semi-physical simulation curves of control system on deep-water work mode(reversed euler method)

图3 浅水工作模式下控制系统半实物仿真曲线(采用正欧拉角)Fig.3 The semi-physical simulation curves of control system on shallow-water work mode(ordinary euler method)

1)采用立式三轴转台进行大姿态控制系统半实物仿真前通过数学仿真可以对转台的角速率限幅值和角加速度限幅值进行计算，从而对转台的角速率限幅值和角加速度限幅值进行合理的设定;同时确定使用的欧拉角定义;

2)某产品在深水控制模式进行仿真时可以采用反欧拉角驱动转台;

3)某产品在浅水控制模式下可以采用常规的正欧拉角进行半实物仿真。

［1］于波，陈云相，郭秀中.惯性技术［M］.北京:北京航空航天大学出版社，1994.YU Bo，CHEN Yun-xiang，GUO Xiu-zhong.Inertial technology［M］.Beijing:Beijing University of Aeronautics and Astronautics Publishing company，1994.

［2］黄雪樵.克服欧拉方程奇异性的双欧法［J］.飞行力学，1994，12(4):28 －37.HUANG Xue-qiao.Dual-euler method for overcoming singularity of euler equation［J］.Flight Dynamics，1994，12(4):28 －37.

［3］李跃军，阎超.飞行器姿态解算的全角度双欧法［J］.北京:北京航空航天大学学报，2007(5):505－508.LI Yue-jun，YAN Chao.Improvement of dual-euler method for full scale eulerian angles solution of aircraft［J］.Journal of Beijing University of Aeronautics and Astronautics，2007(5):505－508.

［4］黄华红，杨云川，吕艳慧.一种鱼雷俯仰角出现±90°时的姿态仿真方法［J］.Torpedo Technology，2012(3):225 －230.HUANG Hua-hong，YANG Yun-chuan，LV Yan-hui.Attitude simulation method for torpedo pitch angle at±90°［J］.Torpedo Technology，2012(3):225 －230.

［5］雷江涛，张秦南，王立文.一种速率陀螺启动过程的时变增益补偿控制技术［J］.舰船电子工程，2012(1):41－42.LEI Jiang-tao，ZHANG Qin-nan，WANG Li-wen.A timevaryin gain compensate control tecnnique for rate gyroscope during its starting period［J］.Ship Electronic Engineering，2012(1):41－42.

［6］王晓晨，赵辉，马克茂，等.一种新型全姿态飞行仿真转台的运动学分析［J］.中国科学:信息科学，2010(4):35 －46.WANG Xiao-chen，ZHAO Hui，MA Ke-mao，et al.Kinematics analyses for a new simulation turn-tables of full attitude flight［J］.Scientia Sinica(Informationis)，2010(4):35－46.