基于高速单体无人艇航行性能的并行优化方法
2014-07-31杨松林王保明
俞 强,杨松林,王保明,于 宁
(1.江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003;2.南京中船绿洲机器有限公司,江苏 南京 210012)
基于高速单体无人艇航行性能的并行优化方法
俞 强1,杨松林1,王保明1,于 宁2
(1.江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003;2.南京中船绿洲机器有限公司,江苏 南京 210012)
基于高速单体无人艇航行性能建立包括快速性、操纵性和耐波性的综合优化数学模型,构造混合的遗传混沌算法(GAPCA)和混沌遗传算法(PCAGA),并编制相关软件对该模型进行综合优化计算,探讨混合算法和单一算法(遗传算法(GA)和混沌算法(CA))优化性能的优劣,同时研究二次载波搜索域区间比例和区间并行次数对优化效率的影响,得到遗传混沌优化算法和混沌遗传优化算法相比单一优化算法寻优效率高,不同算法对应于不同的最佳二次区间搜索比例。
水面无人艇;航行性能;综合优化;遗传混沌算法;混沌遗传算法
0 引 言
船舶优化设计是一个涉及多学科多领域多目标的综合设计优化问题,这种寻找最优设计过程中往往需要对变量的可行域进行大量搜索[1]。近年来遗传算法和混沌算法在船舶工程优化问题得到了一定的应用,国内有冯佰威结合国外舰船研制领域中多学科优化的典型应用,提出了适合我国舰船研制模式的计算环境体系结构[2]。唐正茂等对船舶概念设计阶段进行了多学科和多目标优化研究[3]。但随着设计考虑因素增多带来设计变量的不断增加,优化耗费的时间会呈现指数倍增长,为了提高优化效率,本文基于高速单体无人艇航行性能综合优化问题,提出了一种基于遗传算法和混沌算法的并行混合优化方法。
1 基于遗传和混沌的并行优化方法
1.1 遗传算法与混沌算法
1)遗传算法(GA)
遗传算法是建立在自然选择和群体遗传学基础上,通过自然选择、杂交和变异实现搜索的方法进行优化,遗传算法对于变量较少的多目标工程设计优化问题寻优的能力很强,但随着种群规模的不断增加,进行同样代数,遗传算法的效率会大大降低,遗传算法的具体步骤如下:
步骤1 确定种群中个体个数,遗传代数,交叉概率和变异概率,初始化种群;
步骤2 通过适应度函数计算种群中个体的绝对适应度,并根据其对个体进行排序,适应度函数为惩罚函数和目标函数的乘积,目标函数是指寻优指标函数,惩罚函数为设计约束的满足程度,惩罚函数的构造策略是基于约束的重要程度构造惩罚因子;
步骤3 通过个体的绝对适应度计算相对适应度和累加适应度,利用轮盘赌方法,优胜劣汰,对种群中个体进行更新,形成新的种群;
步骤4 对种群中的个体进行交叉,交叉方法采用非对称交叉方法,对种群中较差的个体进行变异得到新的个体基因,增加种群得到最优个体的概率,重复步骤2。
2)混沌算法(CA)
混沌优化算法通过混沌变量来实现,最常用的是基于logistic映射混沌优化方法。
步骤1构造混沌因子,选取一个X0,取值为0~1之间的数,但是不能等于0.25,0.5,0.75,(混沌奇点),带入logistic模型进行初值映射:
xn+1=μxn(1-xn)。
(1)式中μ为控制参数。不难证明,当μ等于4时处于完全混沌状态,利用混沌对初值的敏感特性,迭代得到多个0~1之间不同初值,称为混沌因子。
步骤2 将混沌变量的值映射到设计变量的空间得到相应自变量的N维向量(N为自变量的个数):
xi=ai+ui(bi-ai),
Xj:Xj={x1,x2,x3,…,xN}→f(Xj)。
式中:i取值范围为1~N;j取值为1~M,M为混沌优化代数。
1.2 基于并行因子的并行算法
传统的优化算法都是对于自变量区间区域整体进行寻优,在自变量个数比较少的情况下,寻优能力比较可观。随着自变量个数增加,寻优能力会大大降低,因此借用计算机学科中并行的思想将设计变量的区间进行等区域划分,每个自变量的区域被分成几个区间块,各个自变量区间块的组合形成一个计算向量空间,假设设计变量的个数为N,划分的区间次数(又称为区间并行次数)为M,每个区间组合中优化计算次数为P,则形成区间的组合为MN方式,总的计算次数W:
W=MNP。
(2)
优化的区域本来是一个N维空间,并行算法实质是对区间的等区域分割,将计算空间进行缩小,因此能大大提高寻优的概率。由于计算的区间向量空间是并行次数的指数函数,所以区间并行次数不是越多越好,合理的选择区间并行次数和每个区间组内的寻优次数是决定并行算法优劣的关键。
借用计算机中数制编码的思想,在程序中引入并行因子的概念,设置并行因子的初值为0000000....00(0的个数为N),让其最低位的0以1的步长进行递增,当某个位上的数达到M则需要向高位进1,同时该位的数重新设置为0,典型的例如并行次数为2时,并行因子进行的是二进制的N位自增运算,一般情况下并行因子的设置与自变量的个数和每个区间组的寻优次数有关,一般选取不会超过4,否则并行算法的寻优优势不能体现。基于并行算法提出下面6种算法:
1)混沌并行算法(PCA):基于并行思想每个区间组中采用混沌算法进行寻优。
2)混沌二次并行算法(PDCA):第一次载波采用区间的并行混沌算法,第二次在第一次选取的4个最优解的一定邻域进行非并行的二次载波,寻取最优解。
3)遗传并行算法(PGA):基于并行思想每个区间组中采用遗传算法进行寻优
4)遗传二次并行算法(PCA):第一次载波采用区间的并行遗传算法,第二次在第一次选取的4个最优解的一定邻域进行非并行的二次载波,寻取最优解。
5)混沌遗传算法(PCAGA):第一次载波采用混沌并行算法,第二次载波采用遗传非并行算法,在第一次5个最优解的一定邻域内寻取最优解。
6)遗传混沌算法(GAPCA):第一次载波采用非并行遗传算法,第二次载波采取并行的混沌算法,在第一次5个最优解的一定邻域内寻取最优解。
2 高速单体无人艇航行性能综合优化模型
2.1 设计变量
综合快速性、操纵性、耐波性的设计变量,本文中高速单体船流体动力学性能综合优化的数学模型选择17个船型参数作为设计变量,分别是:船长L,船宽B,吃水T,方型系数CB,中横剖面系数CM,设计水线面系数CW,浮心纵向位置LCB,螺旋桨直径DP,盘面比AE/AO,螺距比P/DP,螺旋桨转速N,设计航速VS,半进水角ie,尾板相对浸湿面积At/Am,纵倾角α,斜升角β,重心距基线高度Zg,将其用向量X表示,即:
X= {X1,X2,X3,X4,X5,X6,X7,X8,X9,X10,X11,
X12,X13,X14,X15,X16,X17}={L,B,T,CB,
CM,CW,LCB,DP,AE/AO,P/DP,N,VS,ie,
At/Am,α,β,Zg}。
(3)
2.2 目标函数
高速单体水面无人艇航行性能的总目标函数用F(X)表示如下:
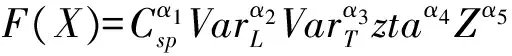
(4)
式中α1,α2,α3,α4,α5分别为快速性、直线稳定性、回转性、纵摇和垂荡指标的权重,并将该指标压缩至0~1之间标准值,且有α1α2α3α4α5=1。
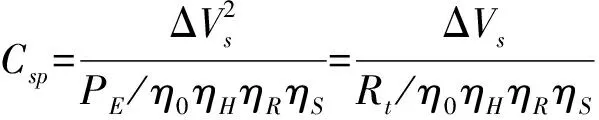
(5)
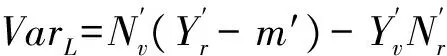
(6)
VarT=D/L。
(7)
借助于Fridsma图谱进行四维插值得出纵摇和垂荡十分之一有义幅值ψ1/10和Z1/10。
2.3 约束条件
1)等式约束
① 满足浮性条件,Δ保持不变,Δ-LBTCB=0;
② 螺旋桨的推力与船舶航行时遭受的阻力平衡;
③ 设计状态下主机供给螺旋桨的转矩必须等于螺旋桨吸收的转矩。
2) 不等式约束
① 各个设计变量的设计取值范围;
② 按海船稳性规范,初稳性高GM,GM>0.7mg;
③ 螺旋桨需满足空泡要求;
⑤ 横摇幅值Φα满足不等式约束条件:Φα=Φα(X)≤10°。
⑦ 满足舒适性条件(主要考虑横摇周期大小):Tφ=Tφ(x)>2.0 s。
3 优化计算及结果分析
3.1 优化计算
高速单体无人艇的航行性能综合优化问题涉及到17个设计变量,包括6个等式约束和7个不等式约束,本文基于此数学模型和上述6种算法基础上编写了计算程序。该高速艇优化设计变量的取值范围如表1所示。
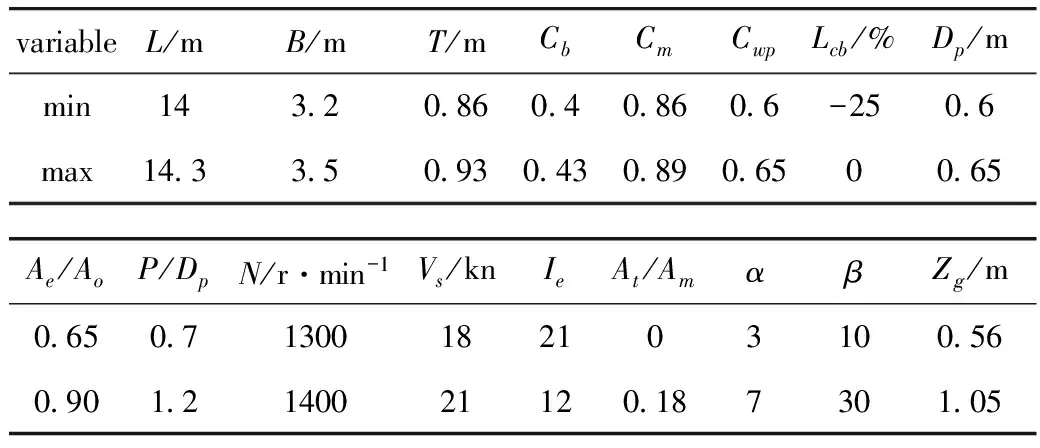
表1 设计变量范围
选取α1=9/7,α2=1,α3=7/9,α4=1,α5=1,这样的选取原则是考虑到高速单体船的快速性、操纵性、耐波性的相对重要性来决定的[4-5],本文在1台计算主频为2.3GHz,内存为2G,硬盘为250G的电脑上进行优化计算。

表2 不同优化方法的计算结果
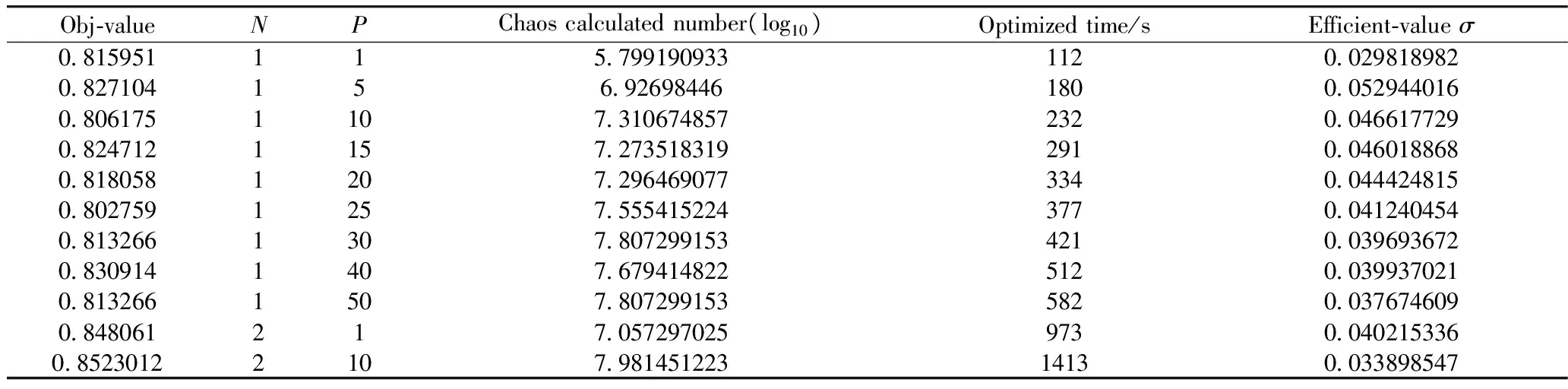
表3 混沌并行算法效率与并行次数N和区间混沌次数P关系表
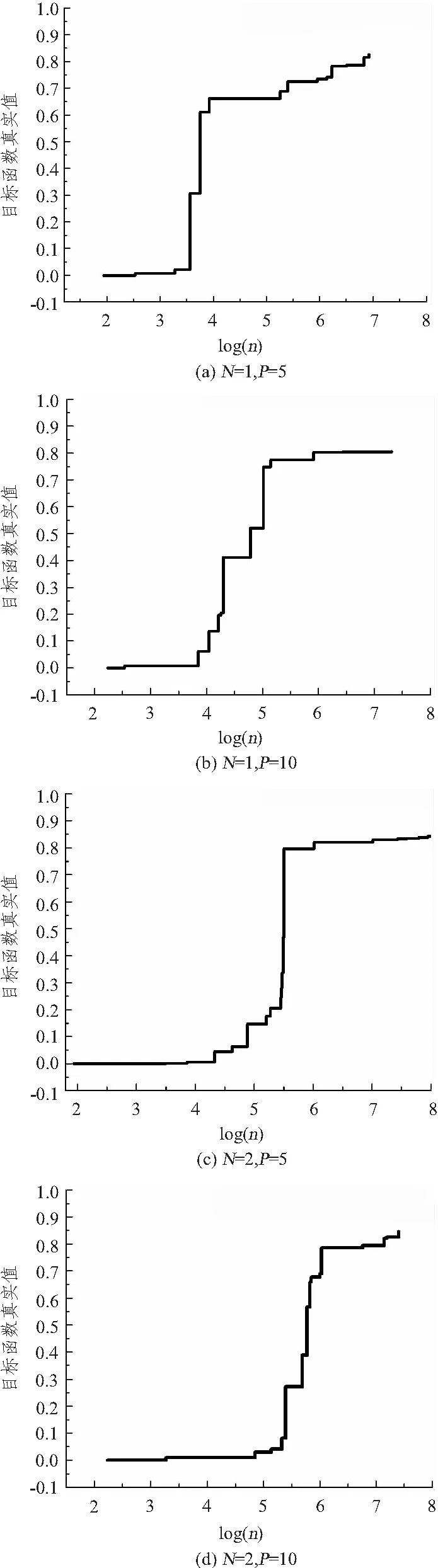
图1 不同并行次数N和区间混沌次数P下目标函数 随着混沌次数对数值变化图Fig.1 Obj-function value increase by chaotic logarithm with different parallel number N and subspace chaotic value P
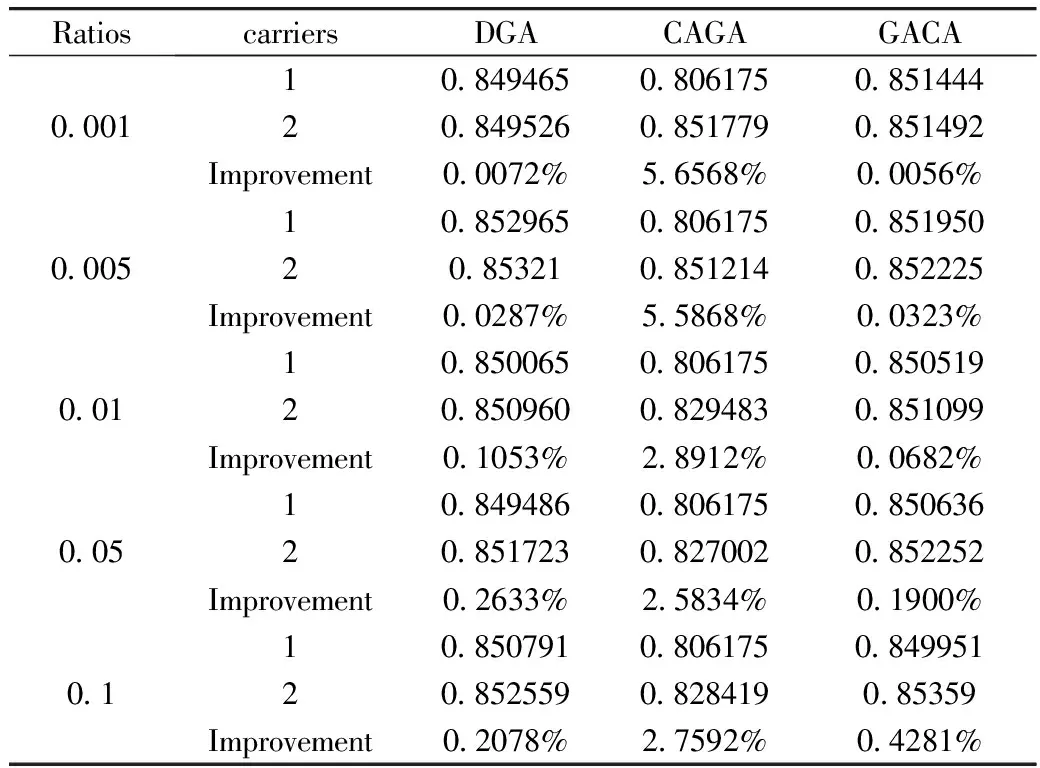
RatioscarriersDGACAGAGACA000110849465080617508514442084952608517790851492Improvement00072%56568%00056%00051085296508061750851950208532108512140852225Improvement00287%55868%00323%00110850065080617508505192085096008294830851099Improvement01053%28912%00682%00510849486080617508506362085172308270020852252Improvement02633%25834%01900%011085079108061750849951208525590828419085359Improvement02078%27592%04281%
3.2 结果分析
1)表1中遗传算法一次载波遗传代数为8 000次,并行混沌算法为混沌一次载波,并行次数取值为2,区间组混沌次数为1,混沌二次载波中第一次载波和并行混沌算法一致,在第二次载波中所选搜索域为原自变量区域的0.001,遗传混沌算法采用遗传算法为8 000代和混沌算法N=1,P=10,搜索域为原自变量区域的0.001,而混沌遗传算法参数同遗传混沌算法,但搜索区域为0.1,遗传二次载波所选区域同样为0.001。通过表1可以看出,6种优化算法的优化结果都比较好,各个约束都达到99%以上,遗传的一次载波虽然搜索精度没有其他6种算法的精度高,但是所花费的时间比较少;并行混沌一次载波和二次载波搜索精度相对于遗传一次载波的有所提高,计算时间大大增加,效率因此会有所降低;遗传算法二次载波在遗传一次载波的基础上继续寻找最优值,但是所消耗时间比较多。遗传混沌算法和混沌遗传算法结合了2种算法优点,遗传对变量范围比较大的情况进行全局寻优能力比较强,而混沌对局部区域的寻优效果很明显,在达到同样的精度的情况下二者寻优所耗费时间比单一混沌算法或者遗传算法少。
2)观察表2,综合优化算法的结果,综合算法的搜索精度和搜索时间与计算次数,定义算法效率值:
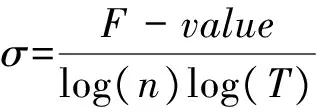
(8)
式中:n为混沌计算次数;T为计算时间;F-value为在对应n和T的情况下所搜索的最优函数值。对于混沌并行算法来说,在N=1的情况下,随着P增加,搜索精度提高并不明显,反而耗费的时间大大增加,效率值在P=5左右达到一个峰值,而当N=2时,搜索精度会很大程度上得到提高,但是效率值提高并不明显。
3)观察图1,比较寻优函数值突增区域可以发现,随着N的增加该区域会产生滞后,N=1、P=5时计算到3 500次目标函数值突增,N=2、P=5时计算到4 300次函数值突增,比较在P=10的2个图像同样出现了滞后增加现象。

图2 优化提高比例随二次搜索域比例变化图Fig.2 Optimization improvement ratio with different secondary search domain
4)遗传算法中全部取1 200代,比较不同二次载波搜索域比例对寻优的影响。二次搜索区域分别选取原区间的0.1%,0.5%,1%,5%,10%,分别选用遗传二次载波、遗传混沌算法和混沌遗传算法3种算法比较两次载波的寻优值,可以发现对于遗传算法二次载波,随着二次搜索区域的扩大,目标函数值优化提高的百分比出现增加,在5%的左右出现峰值,遗传混沌算法的优化提高百分比一致增加,且增加幅度越来越大,混沌遗传算法优化的目标函数值提高幅度却随着搜索域的增加而减少,混沌遗传算法的二次载波最优值提高的幅度比例大大优于其他2种算法。
5)遗传算法初始种群时是利用随机数进行初始化,因此每次载波计算的结果都不相同,而混沌算法只要混沌初值一定,对应的混沌计算轨迹会一致。相对于选用混沌算法,第一次载波选用的遗传算法可以降低优化陷入局部最优的可能性,以最快的速度找到最优值可能存在的区域,而合理的选取二次载波区域。如果选取混沌算法,利用混沌局部寻优的优点,可以在一定的时间内找到更好的最优值;如果选取遗传算法,寻优效率没有混沌算法高,计算时间长,且寻优值也低于混沌算法。
4 结 语
综上所述,本文在一种高速单体无人艇数学模型的基础上,应用上述6种算法进行了无人艇航行性能的优化计算,在达到同样寻优精度的情况下,遗传混沌算法和混沌遗传算法的寻优效果都比单一的算法好得多,该方法为船舶优化设计提供了一种重要思路[6]。在船舶设计中,并不是所有的设计变量对船舶的综合性能具有相同的重要性,有些设计变量存在平行关系和从属关系,因此可以选取重要的设计变量进行优化计算,同时对于带有系统可靠性设计的优化,怎样构造带有随机性设计优化数学模型[7],需要下一步的研究。
[1] YANG Song-lin,CHEN Shu-lin,ZHU Ren-qing,et al.A kind of design method of ship form parameters of large ship based on the best comprehensive performance[J].Ship Mechanics,2005,9(6):56-62.
[2] FENG Bai-wei,LIU Zhu-yuan,CHANG Hai-chao,et al.Study of multidisciplinary integrated optimization computing environment in ship design[J].Ship Mechanics,2009,20(2):5-8.
[3] TANG Zhen-mao,JIE De,MA Shi-hu,et al.Study of ship the conceptual design stage of multidisciplinary and multi-objective optimization[J].Ship Mechanics,2010,14(8):879-886.
[4] YANG Song-lin,CHEN Shu-lin,XI Wei,et al.Research of fuzzy chaos algorithm and its application in ship performance or structural characteristics comprehensive optimization[J].Ship Mechanics,2007,11(2):208-213.
[5] WU Yan,YANG Song-lin.Research of principal dimensions limited ship performance and structural features comprehensive optimization method[C].2009 Academic Conference Proceedings of the National High Performance Computing,2009:303-306.
[6] LU Chong-hong,LIN Yan,JI Zhuo-shang,et al.Application of genetic algorithms in the application of the calculation of ship free floating state[J].Journal of Shanghai Jiaotong University,2005,39(5):701-705,710.
[7] HAO Cui,OSMAN T.Application of a new multi-agent hybrid co-evolution based particle swarm optimization methodology in ship design[J].Computer-Aided Design,2010:1013-1027.
Parallel optimization method based on navigation performance of high-speed single hull ship
YU Qiang1,YANG Song-lin1,WANG Bao-ming1,YU Ning2
(1.Jiangsu University of Science and Technology, Zhenjiang 212003,China; 2.China Ship New Oasis Machinery Company,Nanjing 210012,China)
The optimization model is established including resistance and propulsion, maneuverability and seakeeping performance. Algorithms of GAPCA and PCAGA are developed while optimization program is written in C++ language in order to conduct optimization calculation based on the model, optimization ability research comparison of mixed algorithms of GAPCA and PCAGA and single algorithms of GA and CA are made while impacts of different secondary search domain ratios on objective function are studied, the conclusion is mixed optimization algorithm shows superior ability while different algorithms to find best objective value correspond to different secondary search domain ratios.
USV;navigation performance;comprehensive optimization;GAPCA;PCAGA
2013-05-20;
2013-07-01
俞强(1990-)男 ,硕士研究生,研究方向为水面高速船总体性能综合优化方法、水下深潜器总体性能优化设计。
U661.1
A
1672-7649(2014)03-0040-06
10.3404/j.issn.1672-7649.2014.03.008
