舰船磁场数值计算方法发展综述
2014-08-26王德强
王德强,余 强
(1.中国人民解放军92786部队,广东 湛江 520464;2.海军工程设计研究局,北京 100070)
0 引言
现代舰船大多由钢铁材料建造,在地磁场和机械力的综合作用下,成为一个巨大的浮动磁体。舰船在地球磁场的磁化下,其周围空间具有一定的磁场,这个磁场被称为舰船磁场。磁性水雷、磁性鱼雷等武器的引信感应到舰船磁场会在舰船附近爆炸,对舰船生命力构成严重威胁,因此,舰船磁隐身是舰船隐身性能的重要指标之一[1]。现代战争中利用舰船磁场对其实施探测和攻击的武器发展十分迅速,如果不对舰船实施有效的磁防护措施将严重影响其生命力和战斗力。
为提高舰船生命力,必须对舰船实施磁性防护。舰船磁性防护的目的是尽一切可能降低舰船的磁性特征,使其在周围空间一定范围内产生的磁场小于磁引信武器或磁探测仪器所设定的动作阀值。舰船磁性防护的前提是全面、准确地了解和掌握舰船空间磁场分布,而衡量磁性防护的指标也必须了解舰船的空间磁场分布。
目前,一般通过磁传感器测量和磁场数值建模来获得舰船磁场。随着电磁场数值计算技术的发展,可用于舰船磁场数值建模的方法已趋多元化[2]。鉴于舰船磁场数值建模的复杂性,如何建立一个精度和稳定性都满足舰船磁性防护需求的舰船磁场数值模型成为磁隐身技术中的一个重要课题。本文在广泛查阅国内外文献的基础上,对舰船磁场数值建模方法进行系统总结,并分析和评价目前用于舰船磁场数值建模中等效源法、广义多级技术、磁场积分法和磁场微分法等几种典型方法。
1 舰船磁场分类及其特点
按照舰船磁场形成机理,可将舰船磁场分为感应磁场和固定磁场两部分。感应磁场随地磁场变化,而固定磁场在一般情况下保持相对稳定。
1.1 感应磁场
钢质舰船在地球磁场作用下,会产生感应磁性,进而在舰船周围产生感应磁场,感应磁场是一种随外界磁场 (主要是地球磁场)变化的磁场,它与舰船实时的位置、航向、姿态等因素有关,因而是一种瞬时效应磁场。舰船感应磁性的大小与下列因素有关:
1)舰船航行纬度区地磁场的大小;2)舰船的航向、纵倾和摇摆;3)造船所用钢材的磁性能;4)舰船形状、尺寸及铁磁设备在船上的分布情况。同一类型的舰船如果建造材料相同,结构相同,则其感应磁性相同。
1.2 固定磁场
船体由许多钢材铆焊而成,船上安装了大量的钢铁设备,造船钢板和铁磁设备本身都具有一定固定磁性。舰船建造组装后,这些钢板和设备的固定磁性迭加起来就形成了舰船总的固定磁性的一部分。这些钢板和设备在舰船建造过程中一直处于地球磁场中,在施工中受到长期机械震动,也必然会产生一定程度的不可逆磁化,从而形成固定磁性的另一部分。另外,在钢板的焊接、切割等局部性的加热、冷却时钢材内部将产生应力,这些应力也会改变局部的磁特性。这样,在舰船下水时就已经形成了自己所特有的固定磁性。
舰船的固定磁性主要在舰船建造时期形成,它与下列因素有关:
1)造船所用钢材的磁特性。钢材的磁特性不同,形成的固定磁性也将不同。
2)造船地区地磁场的大小。地磁垂向分量大的地方,形成较大的垂向固定磁性,地磁水平分量大的地方,形成较大的水平固定磁性。
3)造船船台的方向。它决定了地磁场对舰船的水平磁化方向。
4)船体及主要铁磁设备的形状。
5)造船工艺等。
舰船在建造过程中,由于上述各种情况不完全相同,因而不同舰船甚至是同类型的舰船其固定磁性也将不同。
舰船固定磁性的固定不变相对于外界的磁化条件不发生大的变化而言。当舰船的磁化条件有较大变化时,其固定磁性将会发生变化。舰船建造期间所形成的固定磁性在首次航行时就会发生一定的变化。这是因为舰船在建造时一直受到一个方向的磁化,而首次航行时舰船受到各不同方向的磁化,加上波浪冲击和机器开动时振动等因素影响,使舰船在新的条件下达到新的稳定磁化状态。舰船经过战斗、炮火射击,受到强烈震动,大风浪袭击以及船体经过较大规模的修理之后,固定磁性也要发生变化。另外舰船更换基地,较长时间航行在另一个地区,其地磁场与原地区有明显的差异,也会使固定磁性发生变化。
因此,由固定磁性在舰船周围产生的固定磁场是在钢材的磁滞效应作用下由钢材的历史磁化形成的磁场,是一种相对稳定的积累效应磁场。
2 舰船磁场数值计算的特点
由于舰船的磁场是受地球磁场这个基本稳定的磁场磁化产生的,则舰船在地球磁场中的磁化可以看作在弱磁场作用下铁磁物质的静态 (准静态)磁化过程,而且其感应磁场部分可以看作地磁场作用下的可逆磁化。另外,所研究的区域主要是舰船的外部区域,所以,可以将舰船磁场的数值计算归属到开域静磁场问题的研究范畴。
简而言之,舰船磁场数值建模可等效为考虑剩余磁化强度时铁磁物体在外磁场作用下的静磁建模问题。因此,电磁场数值技术中的静磁建模方法均可用来进行舰船磁场数值建模,但由于舰船结构、尺寸和设备的复杂性及多样性,将电磁场数值计算方法直接应用于舰船磁场数值建模存在一定困难,舰船磁场数值建模的不利因素为:
1)舰船磁场数值建模为开域问题;
2)复杂的物理结构给几何建模和剖分增加了难度;
3)铁磁设备和舰船壳体的尺寸相差很大,甚至达到10-4;
4)材料的多样性给铁磁材料磁性参数的确定增加了困难;
5)考虑剩余磁化强度的舰船磁场数值建模技术存在模型稳定性问题;
6)剖分单元较多的舰船几何网格模型对计算时间提出了更高的要求。
上述不利因素限制了不同电磁场数值计算方法在舰船磁场数值建模技术中的应用,如有限元法在处理开域问题时需对区域边界进行特殊处理、磁场积分法形成的系数矩阵为满阵求解时需花费大量的时间、等效源法存在建模稳定性问题等[3]。
然而,舰船磁场数值建模也存在有利因素。在一定工程精度要求下,舰船磁场数值建模大多数情况不需考虑电流线圈的作用,激励源仅为地磁场,与强电流产生的磁场相比,地磁场为弱磁场,弱磁作用下的磁化点处于铁磁材料的线性磁化区,因此铁磁材料磁性参数的线性化使得舰船磁场数值建模问题可大大简化。
由于舰船磁场数值建模所具有的独特特点,通用商业软件如Ansys、Ansoft等直接应用于舰船磁场建模相对困难,特别是考虑剩余磁化强度的磁场建模,采用磁场逆问题的思路来研究需对软件进行二次开发。因此,国内外学者都从舰船磁场数值建模的特点出发,基于电磁场理论来对舰船磁场数值建模技术展开广泛的研究。
3 舰船磁场数值计算方法
由国内外舰船磁场数值建模技术资料来看,应用较为广泛的建模方法有等效源法、广义多级技术、磁场积分法和磁场微分法。
3.1 等效源法
所谓等效源法[3],即是在求解的场域之外,用一组虚设的模拟源来代替原问题中比较复杂的磁化物体,使模拟源在求解区域产生的场来等效实际磁化物体产生的场,如图1所示。

图1 等效源法求解舰艇磁场数值建模示意图Fig.1 Equivalent source method for calculating warships magnetic field numerical modeling
在磁场等效源法中,常用的模拟体为磁荷、磁偶极子、均匀磁化椭球、磁化电流等。这些模拟体的分布参数一般需根据对问题的定性分析及计算经验人为确定,模拟体的磁性参数则由已知边界上的情况或测量值来确定。当模拟体的分布参数和磁性参数确定后,求解区域内任意点的磁场值就可解析出来。
由于等效源法具有实施简单灵活、编程易于实现、计算时间短且具有一定工程实用精度等特点,磁场等效源法已广泛应用于舰船磁场数值建模中,如舰船磁异常在不同深度的换算。然而等效源法在应用中也表现出其不足之处,如模拟体的分布参数直接决定着等效源法计算精度及模型稳定性,这给舰船磁场数值建模的通用化、实用化带来了困难。目前一般通过以下措施增强等效源法的通用性:对模拟体分布参数优化可减少人为因素的干扰,有效提高磁场模型的稳定性[4];采用正则化技术可降低测量噪声对建模结果的影响[5]。
3.2 广义多级技术
20世纪80年代中期,一种数值法和解析法的结合——半解析法应运而生,即广义多级技术,也称为级数法、多级子法、多级理论、圆 (球)形等效源法、新型等效源法[6]。广义多级技术对计算机资源要求较少,既不需要离散场域,也不需要离散边界,而且对于某一类问题可用统一格式获得高阶可导的连续解。其基本原理是:将偏微分方程中的未知函数,用一系列满足该偏微分方程的本征函数特解展开,确定该通解中待定系数的方法采用点匹配法,并根据经验总结出一些使用规则。
从国内外文献可以看出,广义多级技术已用来解决三维静态电磁场问题[7-9],且国外已将其应用于舰船磁场数值建模技术领域,如基于磁多级子成像技术来重构舰船磁性状态等[10-12]。
最近,美国科学家Alexander V.Kildishev等人研究了一系列潜艇磁场多极成像方面的课题,主要是将磁源的标量磁势在扁平旋转椭球体坐标系下展成谐波形式,其谐波系数即描述了磁源的多极特征,然后用外部磁场的测量数据来求得谐波系数,进而可以得到用级数表示的磁场多极展开式。这些研究在潜艇外部磁场的分析方面取得一定进展,但是建立在假设艇体为扁旋转椭球体近似的基础之上,对于水面舰船的分析还没有相关资料。
从总结出的规律看,由于缺乏理论指导,使求解结果受制于使用者的经验,因此,广义多级技术在舰船磁场数值建模中还没有得到广泛的应用。
3.3 磁场积分法
磁场积分法主要包括积分方程法和边界积分法两类。
1)积分方程法
就积分方程法而言,它从宏观的角度来描述场,场区中每点场值仅取决于所有场源对它的影响,即一次场源 (激励源)和二次场源 (磁化源),再通过毕奥-萨伐定律将场点和源点联系在一起,建立以场点场量为未知量的代数方程组,求解上述该方程组即可获得整个求解区域的解,如图2所示。
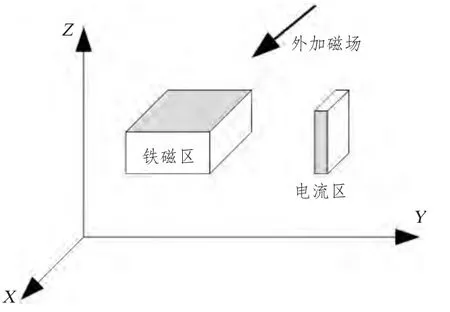
图2 积分方程法建模示意图Fig.2 Integral-equation methods for modeling
选择不同的场点场量,如磁化强度、磁场强度、磁标势 (简化势和全标势)、磁矢势等,可得到不同的代数方程。根据特定的问题,选择不同场点场量作为求解变量可有效简化问题的求解。由于积分方程法将磁化介质视为二次场源,所以其具有离散仅限于磁性介质区、便于处理开域问题且不需考虑边界条件的优点[13]。
国内外资料表明,积分方程法已在舰船磁场数值建模技术中得到了广泛的应用,如法国LEG公司以闭环消磁技术为对象,将积分方程法成功应用于求解舰船薄壳体的磁场数值建模[14];我国也对积分方程法在舰船磁场数值建模中的应用展开了较为广泛的研究,且取得了较多成果[15-16]。
积分方程法从宏观的角度来描述场,场区中每点的磁场值取决于所有场源对它的影响,场点和源点的联系是通过毕奥-萨伐定律实现的。离散只需在非线性铁磁区域中进行即可,这使得数据输入和网格剖分大为简化,所以它能够较好地解决开域问题及连续场的计算问题。但是,积分方程法虽很易于处理开域问题,但也有不足之处,用积分方程法求解非线性问题时,考虑到船体比较大,离散的单元可能比较多,而且确定物质磁化状态的离散方程的系数矩阵是非对称满阵,加上每一剖分单元重心上的场参数是用向量来描述的,在三维场中每一单元重心上形成3个未知数,因此需要相当大的内存来存储系数矩阵的元素。此外,单元间耦合系数的求取也要消耗大量机时,而且铁区中的介质参数要反复迭代求解,要耗占大量的CPU时间和内存,当舰船复杂铁磁材料离散单元数越多时,其求解时间和所需内存将成指数增加,所以一般只能兼顾计算精度和计算时间来取适当的离散单元数,这也一定程度上制约了积分方程法的应用。在舰船磁场数值计算中若单独应用积分方程法最好采用一些方法来对其进行改进,比如利用小波矩量法和快速多极技术等方法。
2)边界积分法
边界积分法也称边界元法。在场域内媒质为各向同性、线性和均匀的条件下,可得直接边界积分法和间接边界积分法 (包括单层源法和双层源法)两类;在分域媒质分界面上可得分界面上的边界积分方程[3]。直接边界元法从等效原理出发,将闭合分界面内的源在场点的磁效应用闭合分界面上的等效源代替;间接边界元法是从叠加原理出发,在边界上设置一组单层源或双层源,用该组源叠加后在场点产生的磁效应来等效替代原始场。间接边界元法与直接边界元法相类似,前者可从后者推导而得,唯一的区别在于前者同一点上只有1种等效源,而后者有2种等效源。
分域媒质上的边界积分法与积分方程法有许多类似之处。二者的区别在于边界积分法采用了分部积分,从而把描述磁场的第二类Fredholm积分方程在一定条件下转化为边界积分方程。除与积分方程法同样的优点之外,其离散只需要在边界进行,因此可降低问题的维数。
国内外文献表明,用边界积分法进行舰船磁场数值建模已展现出其方便性,因此也得到了广泛的应用,如文献 [17-19]采用边界积分法对舰船壳体感应磁场进行了数值建模,计算结果与实验结果表现出很好的一致性。
虽然边界积分法在舰船磁场数值建模中具有离散简单、可降低维数等优点,但其形成的系数矩阵也为不对称满阵,当离散单元较多时,需花费较多内存和求解时间。
由磁场积分法的上述过程可以看出,磁场积分法是一种适用的舰船磁场数值建模方法。从目前最新研究进展可以发现,快速多级子技术[20]、小波稀疏化矩阵技术[6]等可用来解决磁场积分法中存在的不足之处,因此,磁场积分法将在舰船磁场数值建模中具有广阔的应用前景。
3.4 磁场微分法
在磁场微分法中最典型的数值计算方法为有限元法。有限元法是以变分原理为基础的一种数值计算方法,它应用变分原理把所要求解的边值问题转化为相应的变分问题,对求解区域进行离散、插值,离散化后的变分问题为普通多元函数的极值问题,进而得到一组多元的代数方程组,求解代数方程组即可得到边值问题的数值解。一般需经过如下步骤[3]:
1)给出与待求边值问题相应的泛函及其变分问题;
2)将连续域离散成剖分单元之和,选择合适的插值函数;将未知的连续函数离散成有限项函数之和,即将无限个自由度的问题离散成有限个自由度问题;
3)求解泛函极值,离散出矩阵方程;
4)用直接法或迭代法等方法求解有限元方程。
由上述有限元法求解边值问题步骤可以看出,找出与边值问题相对应的变分问题是有限元法的关键。利用有限元法求解边值问题过程中,形成的系数矩阵是稀疏阵,随着求解大型稀疏方程组数值技术的发展,有限元法在众多领域得到了较多的应用。文献 [21-24]表明,由于舰船磁场数值建模属于开域静磁场建模问题,直接应用有限元法进行求解需对区域边界进行特殊处理。
目前国外一些商业有限元软件也可以用来计算舰船感应磁场,比如OPERA有限元软件与TOSCA分析软件被多个国家的海军用于舰船感应磁场建模;另外,由CEDRAT开发的FLUX3D有限元软件也已经被用于研究舰船磁特征,该软件可以采用薄壳单元对薄钢板外壳的船体结构进行感应磁场建模,并且可以计算消磁线圈的绕组效率。但是这些商用软件的价格十分昂贵,功能也较为有限,而且难以实现利用测量值对计算结果进行修正的功能,这在一定程度上限制了这些软件的推广。
有限元法是用有限个自由度来近似描述一个连续体。在开域问题中,研究区域为整个空间,则必须把边值为0的边界取到相当远处,这会使网格和节点数变得非常多 (据称,该软件对舰船的剖分单元数达到100万以上),这使计算机内存和CPU时间消耗非常大,如此巨大的数值求解系统可能难以用于舰船磁场测量的数据处理工作。所以在要研究的开域问题中单独应用有限元法需要进行一些等效边界条件的处理。通过保角变换将开域问题映射为闭域问题可方便利用有限元法来进行舰船磁场数值建模研究。此外,逆矢径变换、有限元法与其他方法混合建模等可弥补有限元法的不足。
4 舰船固定磁场数值计算的理论难点
舰船固定磁场的求取一般只能用反演的方法,可以归属到磁场逆问题的计算范畴,磁场逆问题在理论上有以下两大难点:
一是解的非唯一性,即有无数舰船区域内磁源分布的解对应于给定的磁场分布,舰船区域内的磁源分布不能由船外的磁场唯一确定,从而这个问题在本质上是不适定的。在磁场逆问题中通常很难获得唯一解,必须加入很多限制条件,才有可能得到磁源参数的唯一解。
二是解的不定性或解不连续依赖数据 (又称解不稳定、病态特性),即使输入极小的噪声或扰动都会引起解的振荡,这种病态趋势随解的参量数目增加而上升,即表征磁源磁化特征的待定变量越多,得到的矩阵方程的病态越严重,它使许多常规求解方法变得不稳定从而失效,会导致磁源参数的解非常不稳定,而且这种不稳定与算法无关,仅提高数据准确性是难以克服这些难点的,只有通过增加信息来修正不稳定,即在求解磁场逆问题时对源区的结构及解的空间参量有某些限制与约束,才能得到在一定范围内合理的唯一解。
在舰船固定磁场的逆问题求取中,面临的一个重要问题是:测量得到的固定磁场垂向分量总和数据很难提供足够的信息来确定一个唯一、稳定的解,想要从理论上精确地求出其剩余磁化强度是非常困难的,只有通过研究固定磁场的变化特征及船体的磁化特点,根据经验或试验结果加入一些限制条件 (包括测量信息和先验信息)才可能分离出固定磁场分量。
4 结语
电磁场数值计算技术的发展,已为舰船磁场数值计算提供了技术基础。鉴于舰船磁场数值计算其独特的特点,选择合适的静磁建模方法来分析研究舰船磁场显得十分必要。根据上述分析可知,各种不同的舰船磁场数值计算方法都有各自优缺点,采用单一的数值计算方法难以彻底解决舰船磁场数值建模问题。舰船磁场数值计算应用背景的多样化,要求必须根据舰船磁隐身技术中特定的应用背景合理选择满足工程精度要求的舰船磁场数值计算方法。
[1]叶平贤,龚沈光.舰船物理场[M].北京:兵器工业出版社,1992.YE Ping-xian,GONG Shen-guang.Ship physics field[M].Beijing:Ordnance Industry Press,1992.
[2]周耀忠,张国友.舰船磁场分析计算[M].北京:国防工业出版社,2004.ZHOU Yao-zhong,ZHANG Guo-you.Ship magnetic field analysis and calculation[M].Beijing:National Defence Industry Press,2004.
[3]盛剑霓.工程电磁场数值分析[M].西安:西安交通大学出版社,1991.SHENG Jian-ni.Numerical analysis of engineering electromagnetic fields[M].Xi'an:Xi'an Jiaotong University Press,1991.
[4]L Shen-dao,X Chang-han,Z Guo-hua.Magnetic model of magnetic objects based on genetic algorithm [C].ICEF,2008.
[5]KAMONDETDACHA R,KILDISHEV A V,NYENHUIS J A.Multipole characterization of a magnetic source using a truncated SVD[J].IEEE Trans.Magn.2004,40(4):2176-2178.
[6]阎照文.电磁场新型等效源法[M].北京:北京工业大学出版社,2003.YAN Zhao-wen.Electromagnetic equivalent source method[M].Beijing:Beijing Industrial University Press,2003.
[7]郑勤红,盛剑霓.三维静电场分析的多级理论[J].华北电力大学学报,1996,10(4):14 -19.ZHENG Qin-hong,SHENG Jian-ni.Multi-level theory of three-dimensional electrostatic field analysis[J].North China Electric Power University,1996,10(4):14 -19.
[8]郑勤红,曾华,解福瑶.用多极理论计算三维静磁场问题[J].中国电机工程学报,2005,10(25):348 -351.ZHENG Qin-hong,ZENG Hua,XIE Fu-yao.Multipole theory for three-dimensional static magnetic field[J].Proceedings of the CSEE,2005,10(25):348 -351.
[9]郑勤红,盛剑霓,解福瑶,等.用二阶矢量位计算三维矢量磁位静磁场问题的多极理论[J].中国电机工程学报,1998,18(4):279 -382.ZHENG Qin-hong,SHENG Jian-ni,XIE Fu-yao,et al.Multipole theory of using second order vector portential to solve three-dimensional static magnetic field[J].Proceedings of the CSEE,1998,18(4):279 -382.
[10]KILDISHEV A V,NYENHUIS J A,MORGAN M A.Multipole analysis of an elongated magnetic source by a cylindrical sensor array.IEEE Trans.Magn,2002,38(5):2465-2467.
[11]KILDISHEV A V,KAMONDETDACHA R,NYENHUIS J A.Prediction of the magnetic field below an axissymetrical planar sensor array with a magnetic source located above the measurement plane[J].DT09,IEEE,2002.
[12]KILDISHEV A V,NYENHUIS J A.External magnetic characterization of marine vehicles[M].IEEE,2000:1145-1147.
[13]樊明武,颜威利.电磁场积分方程法[M].北京:机械工业出版社,1988.FAN Ming-wu,YAN Wei-li.Electromagnetic field integral equation method[M].Beijing:MechanicalIndustry Press,1988.
[14]CHADEBEC O,COULOMB J L,BONGIRAUD J P,et al.Recent improvements for solving inverse magnetostatic problem applied to thin shells[J].IEEE Trans,Magn.,2002,38(2):1005 -1008.
[15]郭成豹,何明,周耀忠.积分方程法计算舰船感应磁场[J].海军工程大学学报,2001(12):72 -75.GUO Cheng-bao,HE Ming,ZHOU Yao-zhong.Integral equation method for calculating ship induction magnetic field[J].Naval University of Engineering,2001(12):72 -75.
[16]周国华,肖昌汉,闫辉,等.基于单元表面积分和微粒群优化算法的铁磁物体感应磁场求解方法[C].全国电工理论与新技术2007学术会议论文集,2007:322-326.ZHOU Guo-hua,XIAO Chang-han,YAN Hui,et al.A method to calculate the induced magnetic field of ferromagnetic objects in a weak magnetic field[C].National Electrical Theory and New Technology 2007 Conference Papers,2007:322 -326.
[17]KAHLER G R,DELLA TORRE E.Minimizing the deformation of a static magnetic field by the presence of a ferromagnetic body[J].IEEE Trans.Magn.1991,27(6):5025 -5027.
[18]RIOUX-DAMIDAU F,BANDELIER B,PENVEN P.Perturbation of a static magnetic field by a thin shell ferromagnetic device[J].IEEE Trans.Magn.1993,29(6):2434 -2436.
[19]RIOUX-DAMIDAU F,BANDEFIER B,PENVEN P.A fast and precise determination of the static magnetic field in the presence of thin iron shells[J].IEEE Trans.Magn.,1995,31(6):3491-3493.
[20]盛新庆.计算电磁学要论[M].北京:科学出版社,2004.SHENG Xin-qing.Computing generality for electromagnetism[M].Beijing:Science Press,2004.
[21]RODGER D,LEONARD P J,LAI H C.Surface elements for modelling 3D fields around thin iron sheets[J].IEEE Trans.Magn.,1993,29(2):1483 -1486.
[22]BRUNOTTE X,MEUNIER G.Line element for efficient computation of the magnetic field created by thin iron plates[J].IEEE Trans.Magn.,1990,26:2196 -2198.
[23]BRUNOTTE X,MEUNIER G,Jean-Paul Bongiraud.Ship magnetizations modelling by the finite element method[J].IEEE Trans.Magn.,1993,29(2):1970 -1975.
[24]DORZE F L,BONGIRAUD J P.Modeling of degaussing coils effects in ships by the method of reduced scalar potential jump[J].IEEE Trans.Magn.,1998,34(5):2477 -2480.
