考虑舵机动力学的旋转导弹指令限幅方法研究*

李想，姜毅，马立琦，周帆，黎兰

(1.北京理工大学 宇航学院，北京 100081;2.北京电子工程总体研究所，北京 100854;3.北京航天发射技术研究所，北京 100076)

0 引言

旋转导弹是指飞行过程中绕自身纵轴不断旋转的一类导弹。旋转导弹具有价格低廉，使用简便，机动性高等特点，适用于各种战场环境，广泛见于炮弹、火箭弹、战术导弹、战略导弹再入弹头等[1-5]。对于旋转导弹来说，导弹的旋转使得舵偏产生的控制力在空间和导弹以同频率旋转[6]。当舵面作正弦偏转，且其频率与导弹旋转频率相同时，就能对旋转导弹产生控制力[6-8]。

对于舵机系统来说，其输入的指令是有范围限制的[9-13]。通常情况下，舵机动力学特性往往是被忽略的，即假设其对指令的响应足够快。在舵机系统的带宽远大于导弹频率的时候，这个假设是合理的[14]；但是当舵机系统的带宽小于导弹频率的时候，忽略舵机系统动力学特性，往往会造成一定的误差[14-16]。对于旋转导弹的舵机系统来说，其通常是与导弹同频率做正弦运动，因此需要对输入到舵机系统的指令做一定的约束。通常需要保证通过限幅后的舵机指令的幅值在输入范围之内，并且尽可能地保持原有指令信号的频率特性和相位特性[6]。

本文先介绍了传统的指令限幅方法和文献[6]提出的限幅方法，并分析了这2种方法针对旋转导弹舵机指令限幅应用的局限性。然后基于文献[6]中的方法，将舵机动力学特性纳入限幅方法的考虑范围，结合文献[14]中针对舵机动力学的补偿方法，提出一个新的考虑舵机动力学的指令限幅方法。最后通过仿真验证了该方法的有效性和实用性。

1 传统指令限幅方法分析

对于输入到舵机系统的指令来说，其幅值大小是限制在一个范围之内的。传统的指令限幅方式为

(1)

如果采用这种传统的限幅方法，可能会产生类似于方波的现象。如图2所示，u0为原舵机指令，设置其幅值随时间增大而增大，指令频率不随时间变化。而取定的舵机限幅值y0大小为2 V，则通过传统限幅方法后的舵机指令为u1。从图2可以看出：当|u0|≤y0时，u1和u0重合，即当原信号幅值未超出设计的限幅值时，传统的限幅方法不对原指令做修改；而当|u0|>y0，传统的限幅方法将对原舵机指令强行限幅，产生类似于方波的信号，并且舵机指令u1饱和部分(即u1维持水平的部分)所占信号周期的比例，随着u0幅值的增大而增大。

图1 传统限幅方法示意图Fig.1 Traditional instruction clipping method

图2 采用传统限幅方法的舵机指令变化Fig.2 Original signal and clipped signal—traditionalinstruction clipping method

旋转导弹在飞行过程中不断旋转，舵机也跟着导弹同频率做旋转运动。通常控制舵机运动的指令为正弦指令，其指令的频率也和导弹保持一致。当正弦指令的幅值大于设计的限幅值时，通过传统的限幅，会出现图2中的类似于方波的舵机指令。而舵机系统对于方波信号的响应滞后较大[6]；并且由于舵机指令u1饱和部分所占信号周期的比例较低，导致舵机响应的幅值较低，这会影响到控制系统对旋转导弹的控制效果。如图3所示，u0为原舵机指令，经过传统限幅方法后的舵机指令为u1，舵机的响应为r1。

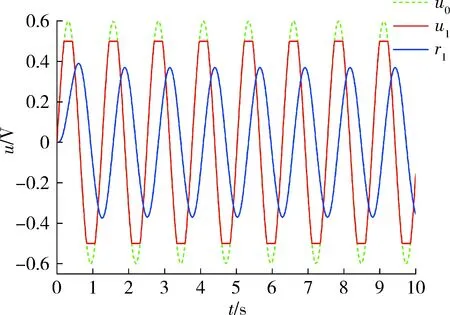
图3 指令与响应曲线(传统限幅方法)Fig.3 Original signal, clipped signal and respond signal(traditional instruction clipping method)

由图3可知，舵机系统对于传统限幅方法后的舵机指令信号的响应能力较差，存在较大的追踪误差，特别是幅值的降低较大，这对于旋转导弹的控制是不利的。

2 基于幅值限幅的限幅方法分析

文献[6]提出了一种新的旋转导弹限幅的方法，其主要思想是在限幅的过程中，构造一个新的正弦指令信号，该指令信号保持原正弦信号的频率相位，并且能够对舵机指令进行限幅。其基本设计步骤如下：

(1) 将限幅前的指令改成正弦函数的标准形式u0=Asin(ωt+φ)，其中A,ω,φ分别为正弦信号的幅值，频率和相位；

采用文献[6]中的方法，可以得到一个新的舵机输入指令。指令在限幅前后的变化如图4所示，u0为原舵机指令，经过文献[6]方法限幅后的舵机指令为u2。

尽管文献[6]的方法可以使新的舵机正弦指令信号保持原舵机指令信号的频率与相位，并且能够限幅。但是如果不考虑舵机的动力学特性，舵机系统对于新的舵机正弦信号的响应并不理想，如图5所示，u0为原舵机指令，经过文献[6]方法限幅后的舵机指令为u2，舵机的响应为r2。

图4 舵机指令变化(文献[6]方法)Fig.4 Original signal and clipped signal(instructionclipping method in reference[6])

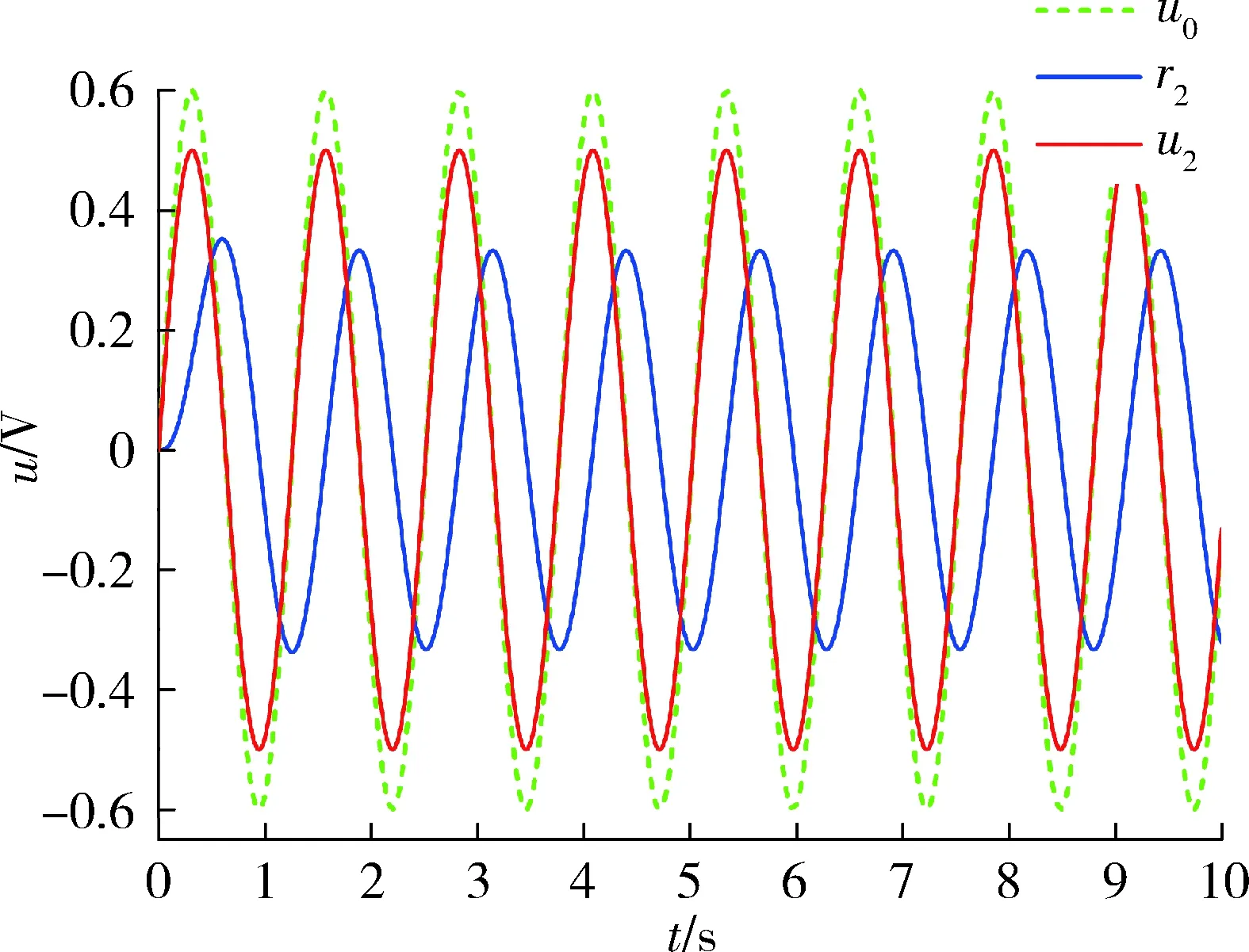
图5 舵机指令与舵机响应(文献[6]方法)Fig.5 Original signal, clipped signal and respond signal(instruction clipping method in reference[6])

由图4可知，采用文献[6]的方法，虽然可以得到一个很理想的舵机指令的输入，但是受到舵机动力学特性的影响，最后舵机系统的响应表现不佳，尤其是其幅值上的跟踪误差很大，这样会对旋转导弹的控制效果产生不良影响。

3 舵机动力学补偿方法分析

通常情况下，舵机动力学是被忽略的，因为舵机系统的带宽往往比导弹的频率大很多。但是，忽略舵机动力学会对控制系统的精度造成影响。传统的限幅方法和文献[6]提出的方法都未考虑到舵机系统对限幅后的舵机指令的响应。为了提高控制系统的控制精度，将对舵机系统的补偿纳入舵机系统的指令限幅的考虑是很有必要的。

文献[14]在时域内考虑典型的一阶舵机模型和二阶舵机模型的动力学特性，并且推导了所对应的舵机模型的补偿增益。其主要的思想就是计算出一个增益M，并且将其直接施加到舵机指令上，来补偿由于舵机动力学而造成的跟踪误差。根据文献[14]推导，对典型的2种舵机动力学系统其增益计算公式如下。

对于一阶动力学系统，若舵机传递函数为

(2)

式中:T为时间常数。

则其对应的增益值为

(3)

式中:Δt为控制系统的采样周期。对于M1，当舵机系统参数确定时，其值为一个常数。

对于二阶动力学系统，若舵机传递函数为

(4)

式中:ωn为无阻尼自然频率;ξ为阻尼比，则其对应的增益可由如下公式计算得出：

(5)

(6)

对于上述式子，若忽略其动态响应过程，仅考虑稳态增益，则对于二阶系统的增益可约等于：

(7)

对于M2，当舵机系统参数确定时，其值同样为一个常数。

4 考虑舵机动力学的指令限幅方法

本文将舵机动力学的补偿纳入到舵机指令限幅中一起考虑。主要思想是，先将原舵机指令用文献[6]的方法限幅，再用舵机补偿的增益放大限幅后的舵机的指令，最后将放大后的指令用传统方法限幅。这样做的话，既可以让最终的指令具备文献[6]中限幅方法的优点，还能减少由于舵机动力学特性而造成的跟踪误差。具体的实施步骤如下：

(1) 将原舵机指令改成正弦函数的标准形式u0=Asin(ωt+φ)，其中A,ω,φ分别为正弦信号的幅值，频率和相位；

(5) 再对u2采用式(1)的方法进行限幅，得到最终的舵机输入指令u3。

如图6所示，u0为原舵机指令，u3为本文限幅所得的舵机指令。需要说明的是，u3并不是方波信号，其本质上是幅值较大的正弦信号经过式(1)限幅后得到的信号。相比于传统的限幅方法来说，此方法将舵机指令幅值放大，让舵机提前进入饱和状态，提高舵机指令饱和部分所占信号周期的比例，从而减少由于舵机动力学造成的跟踪误差。

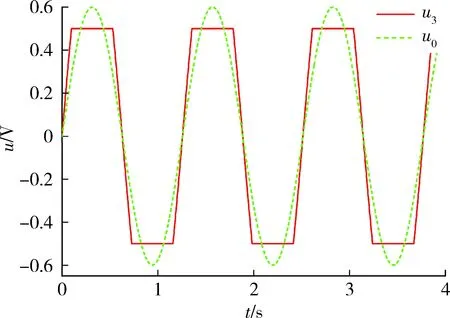
图6 考虑舵机动力学的指令限幅Fig.6 Original signal and clipped signal(instruction clipping method considering actuator dynamics)

5 仿真校验

本小节中，传统限幅方法，文献[6]的限幅方法和本文所提出的方法的限幅效果和舵机响应的跟踪误差将通过仿真来呈现。首先设置限幅前舵机指令为

u0=0.6sin(5t+0),

(8)

式中：u0单位为V，而设计的限幅值y0=0.5 V，假设舵机为二阶动力学系统，且其传递函数为

(9)

则可以仿真得到通过3种限幅方式后的舵机指令，如图7所示，u0为原舵机指令，u1为传统限幅方法后的舵机指令，u2为经过文献[6]方法限幅后的舵机指令，u3为经过考虑舵机动力学的限幅后的舵机指令。

从图7可以看出，相比于传统的限幅方式，采用考虑舵机动力学的限幅方法所得到的的舵机指令u3的饱和部分(黑线水平部分)所占比是最高的，u1次之(蓝线水平部分)，u2基本没有饱和指令(红线水平部分)，也就是说本文的方法能够让舵机指令快速达到饱和。与此同时，u3还具有和u2相同的相位、频率。需要强调一点的是，u3并非为方波信号，本例中，由于舵机所对应的增益M较大，故将限幅前的舵机指令幅值放大较多，导致出现类似方波的现象，但是u3本质上仍然是正弦波的一部分。

3种方法对应的舵机响应如图8所示，其中u0为原舵机指令，r1为传统限幅方法下的舵机响应，r2为经过文献[6]的方法后的舵机响应，r3为经过考虑舵机动力学限幅方法后的舵机响应。

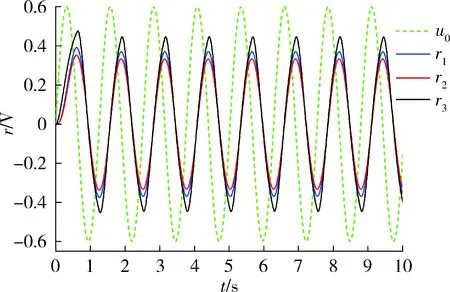
图8 3种限幅方法的舵机响应Fig.8 Original signal and respond signals of three methods

从图8可以看出，采用考虑舵机动力学的限幅方法所得到的舵机响应r3具有最小的跟踪误差，尽管其相对于原舵机指令存在一定的偏差，但是其相对于其余2种方法来说，幅值有了很大的提高，基本已经很接近y0值。其主要原因是当考虑舵机系统的补偿之后，对舵机的利用率提高，舵机满偏的时间更长。同时，r3和r2具有相同的频率和相位。其主要原因是采用考虑舵机动力学的限幅方法是在文献[6]的基础上提出的，其继承了文献[6]方法的优点。

6 结束语

通过分析，采用传统的限幅方法，不能完全发挥出舵机的能力，舵机的响应存在一定的误差；而文献[6]中的限幅方法，虽然能保证输入舵机的指令有和旋转导弹同样频率的指令，但是使用这种方法，舵机系统的响应信号的幅值降低较大，不利于控制系统的控制精度。本文在文献[6]的方法上，结合文献[14]的部分推导，提出了考虑多及动力学的限幅方法。通过仿真验证，该方法不仅具备文献[6]中限幅方法的优点，同时还能提升舵机系统的响应信号的幅值。相比前2种方法来说，其追踪误差最小。该方法计算简单、容易实施、效果较好，能增高旋转导弹对舵机系统的使用效率，为旋转导弹的控制建立了良好的基础。