基于限幅法抑制合成干扰信号的峰均比研究

2018-06-19李海涛

舰船电子对抗 2018年2期

李海涛，杨娟

(西安电子科技大学，陕西西安 710071)

0 引言

在雷达干扰系统中，合成干扰信号的峰均比是影响雷达发射机效率的重要因素[1]。当很多个射频噪声基带信号进行矢量叠加时，合成信号的包络起伏会变大，瞬时功率会急剧增大，甚至远大于信号的平均功率，这就会导致较高的峰均比[2]出现。由于功率放大器为非线性器件，合成信号经过射频功率放大器后，这就会导致具有较高峰值的信号处于功率放大器的饱和区，不会被放大甚至会限幅，这样一来就会大幅度降低功率放大器的效率；另一方面，当输入具有较大峰值的信号时，就要求雷达干扰系统的器件有较大的动态范围，这就会对模数转换器(ADC)和数模转换器(DAC)的性能有更严格的要求[3]。因此，研究合成信号的峰均比问题在雷达干扰领域具有重要意义。

1 合成信号的峰均比概述

1.1 信号合成理论

数字信号的表达式可以用复指数的形式来表示：

si(n)=Aiej((ω0+ωi)n+φi)

(1)

式中：Ai为幅值；ω0为中心频率；ωi为频率变化率；φi为初相位。

假设参与合成的N个信号是相互独立的，则同时多信号的数学表达式为：

(2)

因此，可以认为任意时刻的合成信号是N个独立复信号的叠加。

根据欧拉公式，复指数可以用三角函数来表示，将式(1)展开，即：

si(n)=Aicos((ω0+ωi)n+φi)+

j·Aisin((ω0+ωi)n+φi)

(3)

那么同时多信号合成的表达式可以表示为：

(4)

若参与合成的数字信号的实部和虚部分别用Ii(n)和Qi(n)来表示，则同时多信号合成的表达式可以为:

(5)

因此，同时多信号的合成也可以理解为是先将信号的实部和虚部分别叠加后，再将其求和得到。

下面对信号合成理论进行仿真。将3路信号进行合成，它们的中心频率分为35 MHz，60 MHz和80 MHz，它们的带宽分别为20 MHz，16 MHz和10 MHz，同时信号合成时的权值都为1。

图1为3路信号的时域合成图，可以看到合成信号的包络呈现出较大幅度的动态变化。图2为合成信号的幅值分布图，可以看到参与合成的信号的的幅值分布大体呈瑞利分布，幅值数量主要集中于某一区域，高幅值的信号个数较少。在实际工程中，由于只有少量高幅值信号的存在，会极大地浪费雷达干扰系统的发射资源。因此，对合成信号进行限幅很有必要。

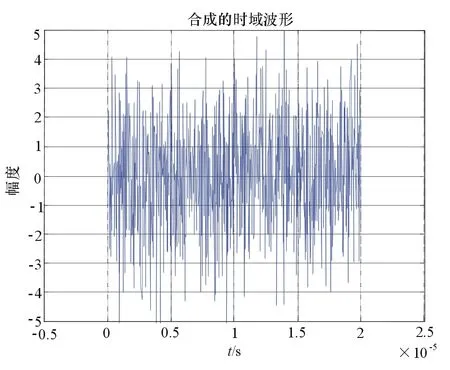
图1 合成信号的波形

图2 合成干扰信号的幅值分布图

1.2 信号的峰均功率比概述

(6)

由于各信号间的独立性，合成信号的平均功率可以认为是每个采样点的幅值的平方作和后再取平均的值，即幅值平方的期望，可表示为:

(7)

式中：E[·]表示取期望。

综上可得合成信号的峰均功率比为：

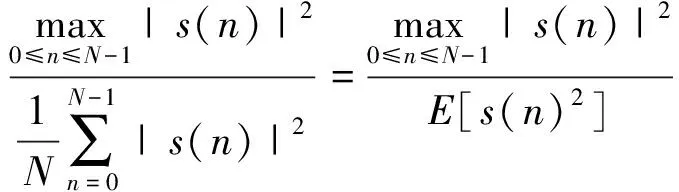
(8)

(9)

若幅值用y表示，合成信号的瞬时功率用z表示，那么z=y2。幅值y服从瑞丽分布，z服从自由度为2的中心卡方分布，均值大小为σ2[4]。它们的概率密度函数分别为：

(10)

(11)

一般而言，通常采用互补累积分布函数(CCDF)来体现峰均功率比的统计特性。CCD是基于累积分布函数(CDF)进行描述的。CCDF定义为信号PAPR值大于某门限值ε的概率，可用下式表示：

FCCDF(ε) =P{RPAP>ε}=1-P{RPAP≤ε}

(12)

式中：P{·}为求概率运算；P{RPAP≤ε}为累积分布函数(CDF)。

CDF意味着所有采样点的幅值均小于门限的概率，其求解可进行如下推导：

P(s(0)≤ε)·…·P(s(n)≤ε)=

(13)

由于合成信号瞬时功率的均值为σ2，即E{|s(n)|2}的值为σ2，那么RPAP的互补累积分布函数可进行如下推导：

1-(1-e-ε)N

(14)

至此，推导结束。PAPR的统计特性可由CCDF来体现，峰均比的分布特性与参与合成的信号数量N有关。

图3条件为当合成信号N取不同值时的互补累积函数曲线，从中可以看出峰均功率比的分布与参与合成信号的数量N有关，随着参与合成信号数量N的增加,CCDF也随之增大,即合成信号的峰均比超过给定值的概率会有所增加。因此，当N较大时，合成信号的峰均比也就越大，有必要对其进行抑制。

图3 合成信号的峰均功率比分布情况

2 基于限幅的抑制峰均比技术研究

2.1 基本原理研究

限幅法主要对合成信号进行一种非线性变换，属于信号畸变技术的一种[5]。该方法是在合成信号进入功率放大器之前对其幅值进行一定程度的限制，也常常被叫做削峰法，进而降低合成信号的PAPR。

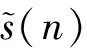
(15)

实际工程中，限幅电平大小通常为值的1到2倍。

下面讨论信号限幅后的PAPR问题。式(9)指出，σ为s(n)所服从正态分布的标准差，也即信号功率均方根的值，具体工程的取值一般由限幅率决定。限幅率(RC)，也可称作限幅系数，是限幅电平和信号功率均方根的比值，表示如下：

(16)

(17)

通过理论推导可以看到，合成信号的峰均功率比与限幅门限具有函数关系。

当限幅门限随着RC的减小而减小时，PAPR会得到很大抑制，但更多的信号被改变幅值，误码率大大提高，所以在实际工程中，PAPR的抑制程度和误码率之间的取舍决定了RC的取值。

限幅是对信号进行的一种非线性处理，根据傅里叶变换，限幅会使原始信号的频谱产生展宽以及带内失真。从另一个角度分析，限幅可以由下列式子进行说明：

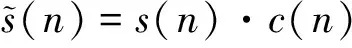
(18)

c(n)=1-p(n)

(19)

(20)

式中:c(n)为窗函数法的时域响应函数;p(n)为对高幅值信号的截断量。

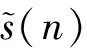
2.2 仿真实验与分析

下面，对以上分析进行仿真验证。仿真(1)条件为：采用3个调频率不同的线性调频信号进行合成，3个信号时长均为1 s，调频斜率分别为100,150和200，起始频率分别为300 MHz，450 MHz和650 MHz，进行合成，包络为Sinc函数。做N=8 192点的快速傅里叶变换(FFT)。合成信号的时域图和频域图的仿真结果如图4和图5所示。

图4 合成信号的时域图

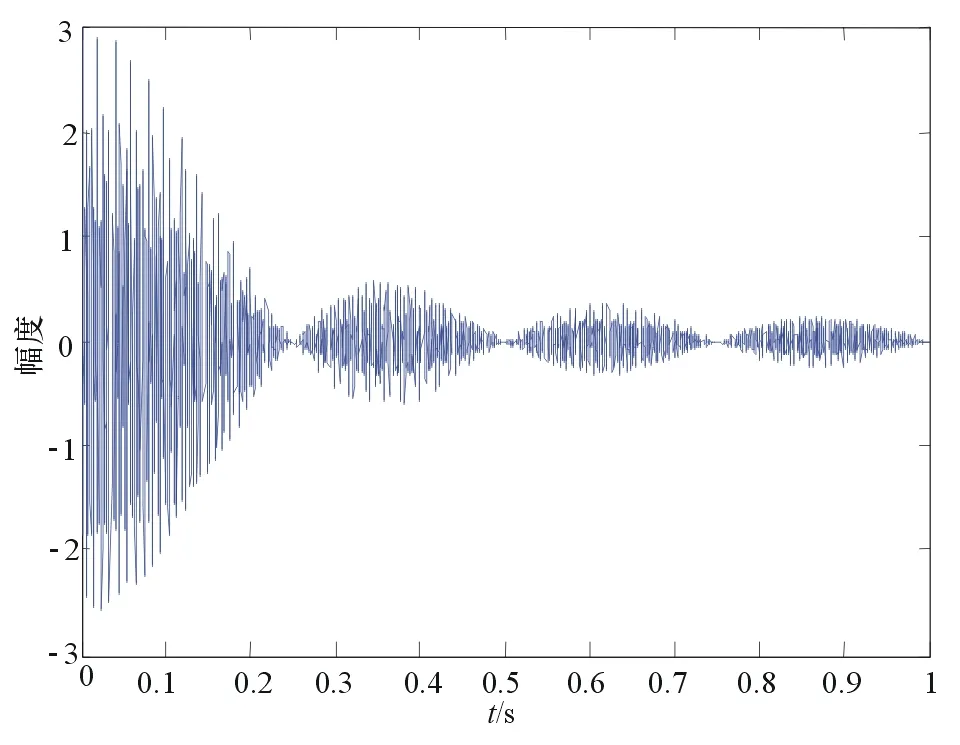
图5 合成信号的频域图

本次仿真，在时域谱中，信号幅值的最大值为3，峰值功率为9，通过对8 192点进行计算得出平均功率为0.367，最终得到仿真条件下合成信号的峰值平均功率比为24.55。在考虑合成信号带宽时，工程中一般以半功率点的频率差值来衡量，为了更加能够描述本仿真结果，本文以频率值为最大值的1/10的点所在的频率差来表示带宽，这样，本仿真中合成信号的带宽为452.6 MHz。

下面对上述的合成信号进行限幅，限幅门限为合成信号最大值的1/2，此时得到限幅后输出信号。仿真(2)输出信号的时域图和频域图如图6和图7所示。

图6 限幅后信号的时域图

图7 限幅后信号的频域图

仿真(2)中，在时域谱中，信号幅值的最大值为1.5，峰值功率为2.25，通过对8 192点进行计算得出平均功率为0.258，最终得到仿真条件下合成信号的峰值平均功率比为8.726，此时的限幅率约为2.954；在频域谱中，可以得到合成信号的频谱带宽为576.2 MHz。

再调整限幅门限，进行仿真(3)，条件为：限幅门限为信号最大幅值的1/5。此时输出信号的频谱图和幅值分布图如图8和图9所示。

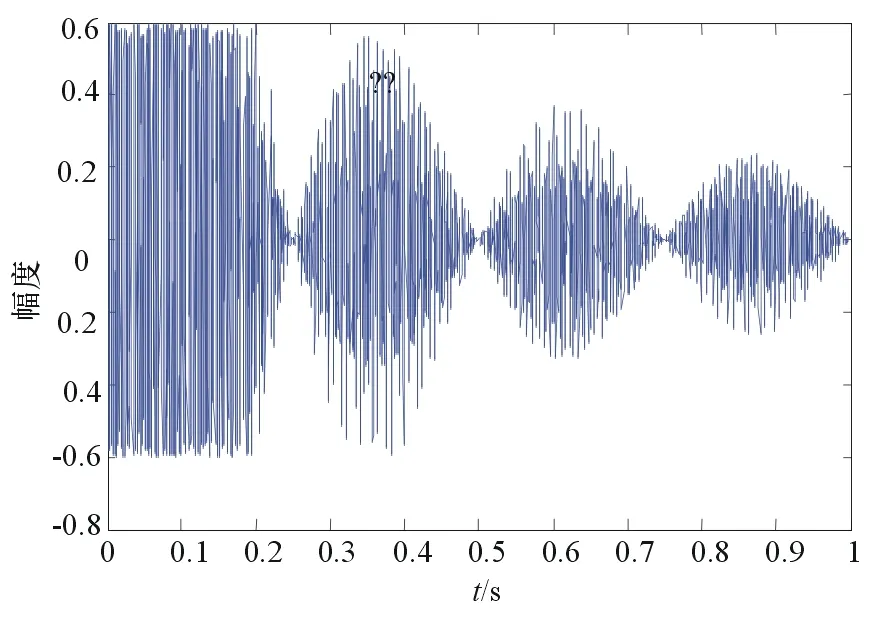
图8 限幅后信号的时域图

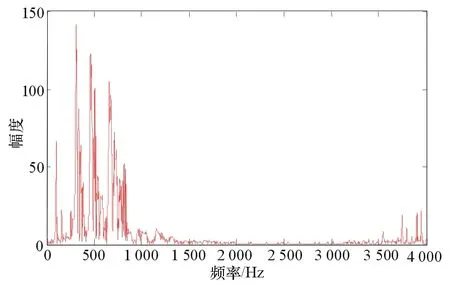
图9 限幅后信号的频谱图

仿真(3)，在时域谱中，信号幅值的最大值为0.6，峰值功率为0.36，通过对8 192点进行计算得出平均功率为0.092，最终得到仿真条件下合成信号的峰值平均功率比为3.905，此时限幅率为1.975；在频域谱中，可以得到合成信号的频谱带宽为750 MHz。

下面仍以仿真(1)的条件作为基本条件进行仿真(4)。条件为：取限幅程度不同的多组实验，限幅程度由门限与信号中最大幅值的比例来描述，得到每组实验中限幅率和频谱带宽的关系图，如表1所示。用限幅后的带宽与原信号的差值作为频谱展宽的主要依据，则频谱展宽程度与限幅率的关系曲线如图10所示。

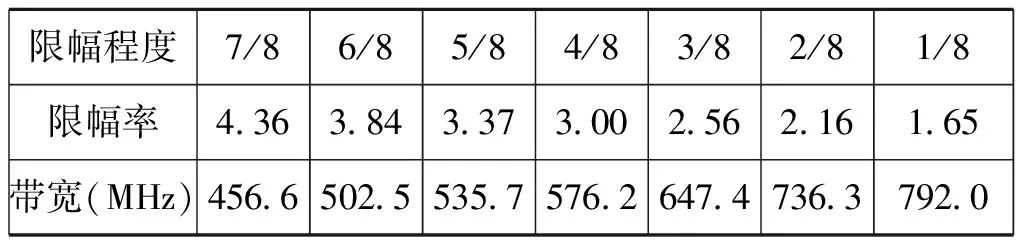
表1 实验中限幅率与频谱带宽的对应关系

通过仿真(1)与仿真(2)对比，得出限幅使得合成信号的峰均功率比得到改善，由原始的24.553改善为8.698；而带宽由原来的452.6 MHz变为576.2 MHz，频谱发生展宽，这就说明信号的能量在频域更加分散了，通过图5和图6也可以直观看出，图5得出原始合成最大幅值接近400，在频率大于1 300 MHz处几乎没有幅值，图6看出限幅后信号的最大幅值介于300与350之间，在带宽内，与原信号相比，幅值均降低了，而在1 300 MHz以外的频率处又出现了幅值较小的新生量。