不同掺剂对水泥土动力特性的影响

，， ，海洋

(1.河海大学 岩土工程研究所,南京 210098； 2.温州大学 建筑与土木工程学院,浙江 温州 325000；3.东营市水利灌溉管理处,山东 东营 257091)

1 研究背景

在我国东南沿海地区广泛分布着软黏土，软土地基抗剪强度低、压缩性高、渗透性低、含水量高并且往往具有流变性和结构性等对抗震不利的工程性质。常用水泥深层搅拌法、水泥高压喷射注浆法、旋喷注浆法等方法，使水泥和软土中的物质组分发生物理化学反应, 形成具有较高强度、较好的稳定性的水泥土桩复合地基，能很好地加固软黏土地基、改善其抗震性能。因此，对水泥土的动力特性的研究很有必要。

小应变时剪切模量Gmax、阻尼比D是体现土动力特性的重要参数，在动力分析中起很重要的作用，也是场地地震安全性评价中不可少的内容。动剪切模量反映水泥土的刚度特性，而阻尼则表示水泥土在振动时能量衰减程度。近十几年很多学者在这方面做了许多研究。袁晓铭等[1]给出了常规土类动剪切模量比和阻尼比随剪应变变化的推荐值，对实际工程起到借鉴作用；Dupas等[2]比较了水泥砂土的静力学和动力学特性，指出水泥土的动应力-应变关系的骨干曲线与土的相同，可以用双曲线模型来模拟；Consoli等[3-5]通过共振柱试验研究了水泥砂土的小应变剪切模量，指出小应变剪切模量是水泥砂土的主要动力学参数；Shambhu等[6-8]进一步研究了水泥土在动三轴试验中的应变软化现象，建立了水泥土的应变软化模型；考虑到水泥对水泥土结构的影响，Rad等[9-10]研究了水泥砂土的胶结作用对水泥砂土动强度、动模量的影响，指出胶结作用提高了水泥砂土的动强度和动模量，水泥土存在临界循环应力比； Frydman等[11-12]在试验基础上建立了水泥砂土的液化模型和线弹性模型，并用于有限元分析。上述都是基于水泥砂土的研究，而关于水泥黏土动剪切模量和阻尼比的试验却很少。

本文利用共振柱来研究在不同水泥掺剂类型、水泥掺量、围压值等条件下，水泥土在低应变幅值和高应变幅值下剪切变形对水泥土动态特性的影响，并尝试建立水泥土的剪切模量和剪应变关系。

2 试验材料及方法

本试验采用GDS制造的底端固定-顶端自由型共振柱来测量水泥土的动力特性。仪器通过电磁驱动系统在试样顶端产生一个正弦扭矩，使试样产生扭转振动，并逐级改变振动频率，测出试样发生共振时的频率。然后让试样振动衰减，测量出土柱振动衰减曲线后，计算出试样的阻尼比。

2.1 试验材料

本试验主要研究普通水泥、矿渣水泥、水玻璃3种掺剂对土的动力特性的影响。试验所用土取自温州市典型的软黏土，软黏土的黏粒(d<0.005 mm)含量为60%，粉粒 (0.005 mm≤d≤0.074 mm)含量为37%，矿物成分主要有：石英、长石、云母，还有少量的方解石、伊利石、绿泥石。软黏土基本的物理指标为比重Gs=2.72，天然含水率ω=65%～80%，液限ωL=57%，塑限ωp=26%。根据试验方案制备水泥掺入比分别为ac=3%，5%，8%，10%，12%，15%，18%的普通水泥土和掺入比为ac=15%的矿渣水泥，以及水泥和水玻璃同时掺加的水玻璃-水泥土(水玻璃掺量6%，波美度19.6)。

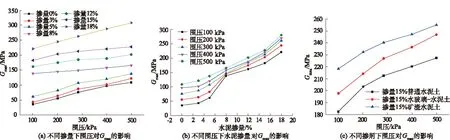
图2 不同掺量、围压、掺剂对Gmax的影响

2.2 试验方法

试验前将所用的土烘24 h后碾碎，过0.5 mm筛，然后按不同水泥掺入比称一定质量的土、水泥和水。将土和水泥混合均匀后加水，制成含水量为60%呈膏状的水泥土，然后将一定质量的土盛入规格为直径ø=50 mm、高度h=100 mm三瓣模中(内壁上事先均匀涂抹一薄层凡士林)，放在振动台上振2 min,使土中气泡排出土样成形均匀。将制好的试样放在恒温(20 ℃±2 ℃)，恒湿环境(湿度95%)中养护28 d。

首先，将制备好的水泥土贴上滤纸，然后套上橡皮膜，安装在共振柱的仪器上。先给试样加5 kPa的围压，橡皮膜与试样紧密贴合，通无气水将管路中的空气排尽。然后，施加围压210 kPa,反压200 kPa,让试样饱和，通过对孔隙压力系数B值检测,都大于95%。再根据试验方案给试样施加不同的等向固结压力σ0，使土样排水固结24 h。最后，利用共振柱仪器通过改变电压值来测出不同围压下的共振频率和阻尼比。

3 试验结果分析

3.1 静力试验

图1(a)为在围压p=100 kPa ,剪切速率ε=0.5%下，水泥掺入比为ac=5%,10%,15%时，水泥土的应力-应变关系曲线。可以看出随着水泥掺量的增加，水泥土的强度不断增大并且增幅明显，掺量为15%的水泥土的强度可以达到1.8 MPa。当ac=5%时，水泥土的应力-应变曲线为硬化形曲线，为塑性破坏；当ac=10%时，水泥土表现出软化现象;当ac=15%时，水泥土的应力-应变关系为明显的软化曲线，表现为脆性破坏。

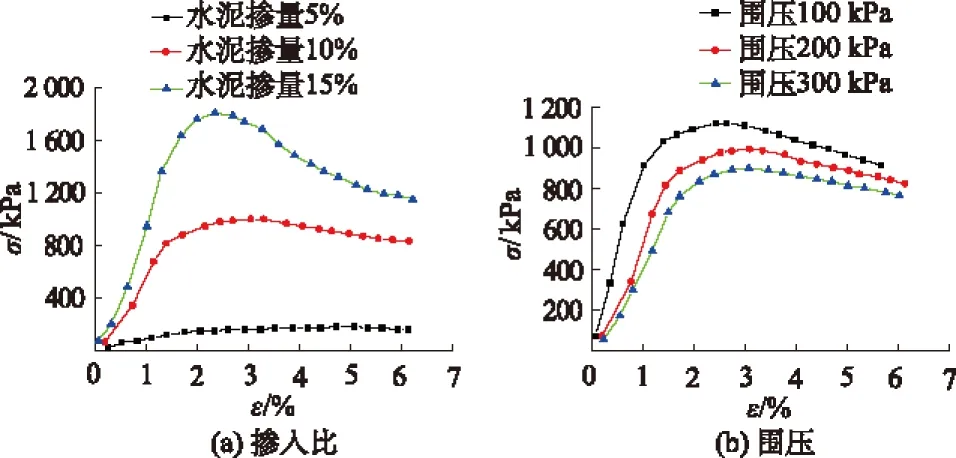
图1 掺入比和围压对水泥土应力-应变关系影响

图1(b)所示为ac=10%、剪切速率ε=0.5%时，在不同围压下水泥土的应力-应变曲线。从图1(b)中可以看出不同围压下,应力-应变关系曲线相似，都为软化曲线。随着围压的增大，水泥土强度也随之增加。由于水泥土的强度已经很大,接近0.8 MPa，围压对强度的影响不明显。

3.2 小应变幅值下Gmax的变化

应变幅值小于0.01%时为小应变幅值，水泥土的动剪切模量和阻尼比都趋于一个稳定值。图2为围压和水泥掺入比对水泥土最大动剪切模量Gmax的影响。从图2(a)中可以看出在同一掺量下水泥土Gmax随着围压的增大而增大，近似成线性关系。但是增长的程度却不同：当掺量在0%～5%范围内，Gmax受围压影响较大，围压500 kPa比围压100 kPa增长了123%～205%。而当掺量在8%～18%范围内，Gmax随围压增长较平缓，受围压影响较小，围压500 kPa比围压100 kPa增长了24%左右。而水泥砂中相同掺入比下围压500 kPa比100 kPa动剪切模量提高了230%[13]。从图2(b)中可看出在相同围压下水泥土最大动剪切模量Gmax与水泥掺量近似成正比例关系，但增长形势却有一些不同：低围压下(100～200 kPa)水泥土的最大动剪切模量Gmax在水泥掺量5%～8%之间斜率陡增发生明显增幅，而在高围压下(300～500 kPa)最大动剪切模量发生较大增幅的范围则集中在水泥掺量为15%～18%之间。陈颖平等[14]在电镜扫描下观察到土料掺水泥后,由于水泥化合物的产生,颗粒表面及颗粒之间存在着纤维状的化合物,该物质填充了土孔隙并增强了土颗粒间的联结,形成了孔隙性较为封闭的结构。当土样中水泥掺量较低时掺剂对土的特性影响较小，还保持有较高的压缩性和灵敏性。结构性不明显，围压对土模量特性影响较大。当掺量较高时，水泥与土颗粒粘结形成骨架，提高了土的抗剪强度，降低了压缩性，围压对土的影响不明显。该结论与陈颖平等[14]试验的结论一致。

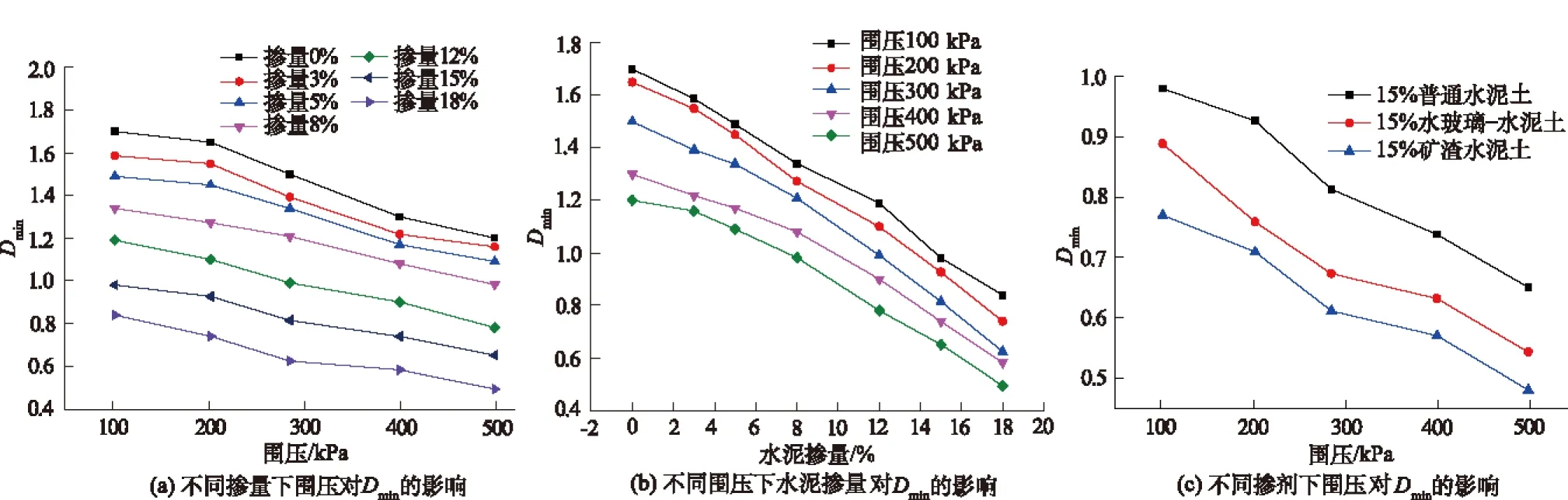
图3 不同掺量、围压、掺剂对Dmin的影响

为了比较不同种类的掺剂对水泥土小应变剪切模量Gmax的影响，本试验选取水泥的掺量为15%。如图2(c)所示，在相同的围压下矿渣水泥土的最大动剪切模量Gmax最大，水玻璃-水泥土次之，普通水泥土的最大动剪切模量最小。原因是矿渣水泥中的矿渣可以促进水泥的水化反应引起土壤颗粒胶结和土孔隙填充的双重效应，使矿渣水泥土的抗剪模量大于其他另外2种。

3.3 小应变幅值下Dmin的变化

从图3(a)可以看出：最小阻尼比Dmin随围压的增大而减小，变化趋势近似为直线，虽然减幅很小但所有趋势线的斜率近似。随着围压的增大，试样逐渐趋于致密，试样由弹塑性向弹性状态转变，在振动过程中试样能量的损耗减少。从图3(b)中可以看出：在相同围压下，随着水泥掺入比增加最小阻尼比Dmin减小，各个围压下减小的趋势和幅值几乎相同。对比图3(a)和图3(b),可以看出:掺入比对阻尼比的影响要比围压对阻尼比的影响明显，这与静力试验中水泥土的特性相同。

对于水泥土，相同围压下高掺量水泥土的Dmin比低水泥掺量的要小，虽然减幅不明显，但规律和趋势很明显。围压和水泥掺量的多少对水泥土的最小阻尼比的影响不明显。从图3(c)可以看出，15%掺量矿渣水泥土的最小阻尼比是3种掺剂中最小的，水玻璃-水泥土次之。原因可能为矿渣可以促进水泥的水化和火山灰的反应，能减小水泥土的阻尼比。水玻璃-水泥土也能从一定程度上比普通水泥土对阻尼比的减小起改善作用。

4 高应变幅值下的试验结果

4.1 水泥掺量对G/Gmax-γ曲线的影响

从图4和图5(a)G/Gmax-γ曲线中看出应变小于0.01%时G/Gmax为一恒定值。当应变大于0.01%时随着围压的增加曲线右移，但掺入比对曲线右移的幅度要比围压明显。这可以用临界剪应变来解释，增大水泥掺入比和增加围压都可以使临界剪应变值增大。说明水泥掺量和围压的增大都可以使土在剪切模量衰减之前承受更大的剪应力，但掺量的作用更明显。

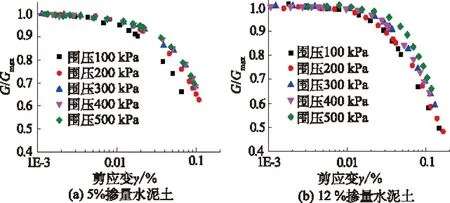
图4 不同围压下G/Gmax-γ关系曲线

在图5(b)中，水玻璃-水泥土的临界剪应变值最大，矿渣水泥土次之。说明水玻璃-水泥土在刚度衰退前要比矿渣水泥土和普通水泥土能承受更大的剪切应变。水玻璃-水泥土和矿渣水泥土都比普通水泥土的动力特性有所提高。当应变大于临界剪应变值后，这些水泥土的刚度退化趋势是相近似的。

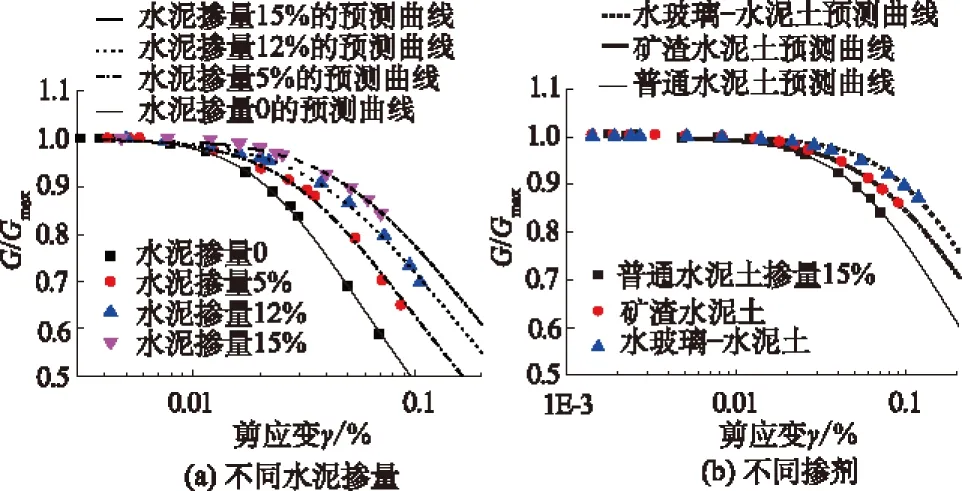
图5 不同水泥掺量和不同掺剂的G/Gmax-γ曲线

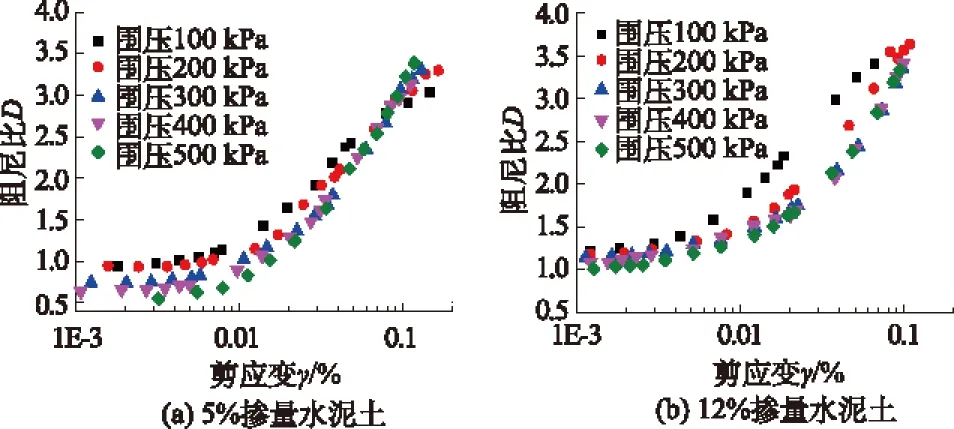
图6 不同围压下D-γ关系曲线

4.2 水泥掺量对D-γ曲线的影响

图6为水泥掺入比为5%和12%的D-γ关系曲线,在应变小于0.01%，阻尼比是一常数且随着围压的增大而减少。当应变大于0.01%时，阻尼比随应变增加而增大且不同围压的曲线变化趋势逐渐重合。

图7(a)不同掺量D-γ曲线中，在应变小于0.01%时，阻尼比值相近D-γ；当应变大于0.01%时，掺量增加剪应变阈值增大，阻尼比曲线右移。水泥的掺量对水泥土的阻尼比也是有影响的。随着水泥掺量的增大，相同剪应变下水泥土的阻尼比减小。这意味着较高的水泥掺量，可以是水泥土在阻尼比增长前承受较大的剪切应变。

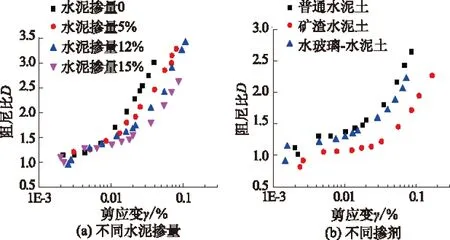
图7 100 kPa下不同掺量和不同掺剂D-γ曲线

图7(b)给出不同掺剂的水泥土的D-γ关系曲线对比。在应变小于0.01%时，普通水泥土的阻尼比要比矿渣水泥土和水玻璃-水泥土的阻尼比大，消耗更多的能量。而矿渣水泥土的阈值却比其他2种大，当应变大于0.01%时，矿渣水泥土的D-γ曲线右移。说明矿渣水泥土在达到相同的剪应变时消耗的能量更少，材料偏于弹性。

4.3 对Ramberg-Osgood模型修正

本试验中高应变幅值的应变数值范围为0.01%～0.1%。当应变低于0.01%时，动剪切模量为一恒定不变值。而当应变高于0.001%时，动剪切模量随着应变的增加而减小，阻尼比随应变的增加而增加。因此，动剪切模量-应变曲线可以近似认为由2个线性阶段构成。第一阶段，剪应变小于临界剪应变，试样在受到循环荷载作用下，剪切模量保持恒定,材料处于可恢复的弹性应变区。第二阶段，应变超出临界应变，动剪切模量在循环荷载作用下会随应变的增长而减小。

根据Ramberg-Osgood动应力-动应变关系曲线,利用最小二乘法对高应变幅值下的试验结果进行拟合。Ramberg-Osgood公式可以很好地表达剪切模量和应变的关系[15-16]。

式中:G是剪切模量；C和R是常数，由材料的性质决定，列在表1 中。

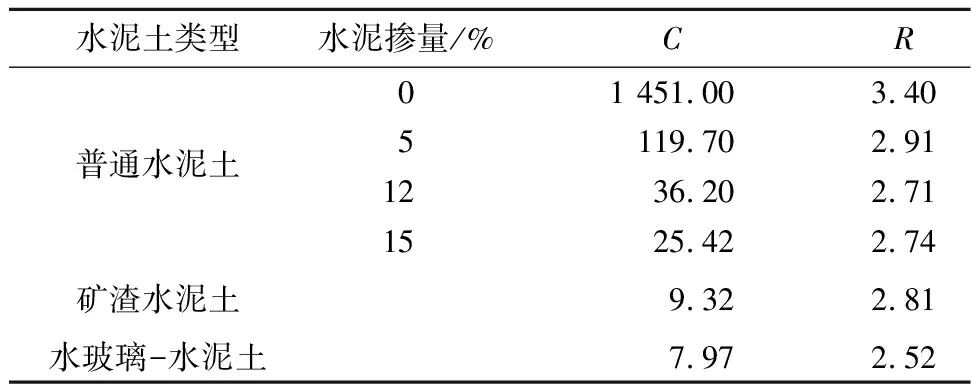
表1 参数C和R取值

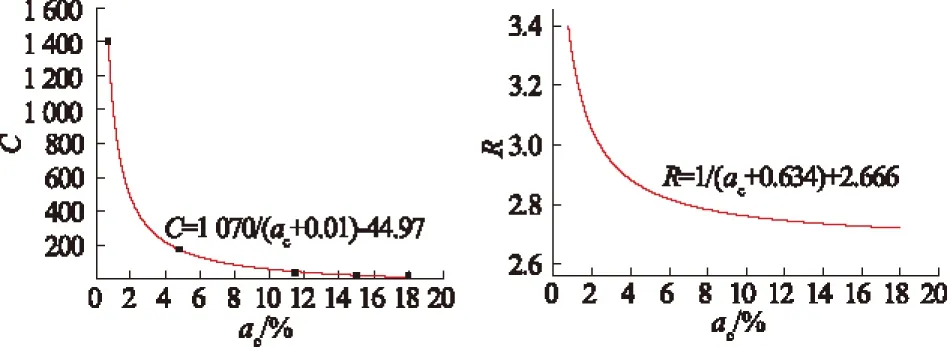
图8 两参数关系曲线及拟合公式

由图8可以看出：C，R值都受水泥掺入比ac变化的影响，随掺入比ac的增加而减小。

根据C,R与ac关系曲线进行拟合，并对Ramberg-Osgood公式进行修正后得

图5中将归一化后的剪切模量-应变的试验值与修正后Ramberg-Osgood模型曲线进行比较。可以看出在一定范围内修正后的Ramberg-Osgood模型能很好地描述剪切模量和剪应变的关系。因此，可以用此公式来预测剪切模量和应变的变化趋势。

5 结 论

本试验中，利用GDS公司的共振柱对取自温州的软土进行不同掺剂土的动力特性影响的测试。通过研究水泥掺量、掺剂类型、围压变化、剪切应变对动剪切模量和阻尼比的影响，可以得出如下几点结论：

(1) 在低应变幅值下，水泥土的围压-剪切模量变化曲线中，斜率的变化范围是0.108～0.194，而在水泥土的围压-阻尼比变化曲线中，斜率的变化范围是从-0.000 85到-0.001 36。在水泥土中围压的变化对动剪切模量和阻尼比不是一个明显的因素。

(2) 随着水泥土中水泥掺量的增加，水泥土的Gmax值增大，水泥土的Dmin值减小。在相同水泥掺量下矿渣水泥土的Gmax值最大，Dmin值最小。

(3) 水泥土的动剪切模量和阻尼比受水泥掺入比的影响比围压的影响大，当掺量大于10%时会对土的结构特性起到明显的改善。

(4) 临界应变值可以用来区分不随剪应变变化的模量Gmax和随应变增加而减小的模量。水泥掺量越大水泥土的临界应变值也相应增大。也就是说，水泥土在模量下降前可以承受更大的剪应力。

(5) 矿渣水泥土的临界应变值要比普通水泥土和水玻璃-水泥土的临界应变值大，可以承受更大的剪应力，在抗剪方面的特性要优于普通水泥和水玻璃-水泥土，抗震特性更突出。

参考文献：

[1] 袁晓铭，孙 锐，孙 静，等. 常规土类动剪切模量比和阻尼比试验研究[J].地震工程与工程振动，2000，20(4)：133-139.(YUAN Xiao-ming, SUN Rui, SUN Jing,etal. Laboratory Experimental Study on Dynamic Shear Modulus Ratio and Damping Ratio Soils[J]. Earthquake Engineering and Engineering Vibration, 2000, 20(4)：133-139. (in Chinese))

[2] DUPAS J M, DECKER A. Static and Dynamic Properties of Sand Cement[J]. Journal of Geotechnical Engineering, ASCE, 1979,105(3): 419-436.

[3] CONSOLI N C, VIANA DA FONSECA A, CRUZ R C,etal. Fundamental Parameters for the Stiffness and Strength Control of Artificially Cemented Sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(9):1347-1353.

[4] ACAR Y B, EL-TAHIR A E. Low Strain Dynamic Properties of Artificially Cemented Sand[J]. Journal of Geotechnical Engineering,ASCE,1986,112(11):1001-1015.

[5] SAXENA S K, AVRAMIDIS A S, REDDY K R. Dynamic Moduli and Damping Ratios for Cemented Sands at Low Strains[J]. Canadian Geotechnical Journal, 1988, 25(2): 353-368.

[6] SHAMBHU S. Sharma and Martin Fahey, Degradation of Stiffness of Cemented Calcareous Soil in Cyclic Triaxial Tests[J].Journal of Geotechnical and Geoenvirinmental Engineering ,ASCE,2003,129(7):619-628.

[7] SHARMA S, FAHEY M. Evaluation of Cyclic Shear Strength of Two Cemented Calcareous Soils[J].Journal of Geotechnical and Geoenvironmental Engineering, 2005, 129(7):608-618.

[8] CHIANG Y C, CHAE Y S. Dynamic Properties of Cement-treated Soils[C]∥Highway Research Record No.379, Washington D C: National Research Council, Highway Research Board, 1972: 39-51.

[9] RAD N S, CLOUGH G W. The Influence of Cementation on the Static and Dynamic Behavior of Sands Report No. 59 [R]. Palo Alto, California: John Blume Earthquake Engineering Center, Stanford University, 1982.

[10] CLOUGH G W, IWABUCHI J, RAD N S,etal. Influence of Cementation on Liquefaction of Sands[J]. Journal of Geotechnical Engineering, ASCE, 1989,115(8):1102-1117.

[11] FRYDMAN S, HENDRON D, HORN H,etal. Liquefaction Study of Cemented Sand[J]. Journal of Geotechnical Engineering, ASCE, 1980, 106(3): 275-297.

[12] LIYANAPATHIRANA D S, CARTER J P, LIU M D. Numerical Modelling of Soft Ground Improved with Cement[C]∥Proceedings of GeoShanghai International Conference 2006:Ground Modification and Seismic Mitigation, Shanghai, China, June 6-8, 2006: 37-44.

[13] PANTAZOPOULOS I A, ATMATZIDIS D K. Dynamic Properties of Microfine Cement Grouted Sands[J]. Soil Dynamics and Earthquake Engineering, 2012, 42(5): 17-31.

[14] 陈颖平，陈云敏，黄 博.循环荷载作用下结构性软黏土特性的试验研究[D].杭州：浙江大学，2007. (CHEN Ying-ping, CHEN Yun-min, HUANG Bo. Experimental Study on the Properties of Structural Soft Clay under Cyclic Loading[D]. Hangzhou: Zhejiang University, 2007. (in Chinese))

[15] 谢定义.土动力学[M].北京：高等教育出版社，2011. (XIE Ding-yi. Soil Dynamics[M]. Beijing: Higher Education Press, 2011. (in Chinese))

[16] 栾茂田.土动力非线性分析中的变参数Ramberg-Osgood本构模型[J].地震工程与工程振动，1992,12(2):69-78. (LUAN Mao-tian. Ramberg-Osgood Constitutive Model with Variable Parameters for Dynamic Nonlinear Analysis of Soils[J]. Earthquake Engineering and Engineering Vibration, 1992,12(2):69-78. (in Chinese))