循环荷载作用下珠海隧道饱和黏土软化试验研究

，，，,

(1.河海大学 a.岩土力学与堤坝工程教育部重点实验室；b.岩土工程科学研究所；c.安全与防灾工程研究所，南京 210098； 2.山东省地震工程研究院,济南 250021)

1 研究背景

港珠澳大桥珠海连接线是国家重点工程港珠澳大桥的重要组成部分，主要由桥梁、隧道构成，其长度占路线总长的96.09%。珠海隧道为高速公路双向六车道超大断面隧道，隧道总长6 195 km，占路线总长的46.12%。其中，拱北隧道是整个工程的重点控制性工程。

港珠澳大桥珠海隧道地基为南方典型的软黏土。黏土地基在长期循环荷载作用下将会引起工后沉降，严重威胁珠海隧道的行车舒适性和安全性。为此，通过室内试验对珠海隧道黏土进行循环荷载下动力软化研究具有重大工程应用价值，研究成果也将丰富珠海饱和黏土动力特性研究，对其它地区黏土地基的动力软化问题也有较好的借鉴意义。

循环荷载作用下土体软化的原因很多，大致可以分为3类[1]：①循环荷载引起饱和黏土产生孔压；②循环荷载引起主应力方向改变导致土体结构重塑；③孔压和土体结构重塑的共同作用。国内外学者对饱和黏土动力软化开展许多研究，取得了不少成果。Vucetic等[2]研究了塑性指数和超固结比对土体软化的影响；Lefebvre等[3]通过试验表明加荷速率能够影响土体软化；Idriss等[4]提出软化指数概念，并且建立循环次数与软化指数之间的关系表达式；Yasuhara等[5]建立循环次数与软化指数之间的半对数表达式。为更确切反映土体软化现象，要明伦等[6]对Idriss等[4]定义的软化参数进行修正。周建等[1]通过动三轴试验研究了循环应力比、超固结比、频率对土体应变软化的影响，并建立了相应的土体软化数学模型；王军等[7]通过开展双向激振试验建立了双向激振循环荷载作用下饱和软黏土的软化模型。

然而,以往的研究对循环荷载的模拟主要以正弦波为主。但Hyodo等[8]的现场试验结果表明，交通荷载作用下地基土受力波形可采用半正弦波来模拟，而正弦波由于拉压等幅，模拟地基所受的动应力与实际情况差别较大。因此，本文采用半正弦波来模拟交通荷载，研究半正弦波荷载下珠海隧道饱和黏土动力软化问题。

2 试验内容和方法

2.1 试验土样

试验土样取自港珠澳大桥珠海隧道茂盛围段详勘原状样，取样深度为8～10 m,其尺寸(直径×高)为100 mm×150 mm，试验三轴试样尺寸为ø50 mm×100 mm，采用切土器切取。试样分别为粉质黏土和淤泥质黏土，基本物理性质指标如表1。

2.2 试验内容

试验仪器为GDS双向振动三轴仪。动力软化试验采用应力控制加载方式。试样制备完成后先进行抽真空饱和，装入三轴仪后再进行反压饱和，饱和过程中进行孔隙应力系数测定，当孔隙应力系数值大于0.95以后对试样进行固结。根据试样埋深，固结围压取100 kPa；根据车辆行驶统计规律，振动频率选取1 Hz。试验过程中轴压、孔压、循环次数、轴向位移等数据由电脑采集处理，试验方案如表2。

表1 试样基本物理性质指标

表2 动力软化试验方案

3 试验结果与分析

3.1 软化指数分析

循环荷载作用下，依据Idriss软化指数δ的定义，并考虑到试验采用应力控制加载方式，软化指数δ的定义为

(1)

式中：GN,max，G1,min分别为第N次和第1次循环次数的土体的最大与最小割线剪切模量；qmin，qmax分别为每次循环中土样的最小与最大剪应力；εN,min，εN,max分别为第N次循环中最小与最大轴向应变；ε1,min，ε1,max为第1次循环中最小与最大轴向应变。

根据试验结果得到软化指数曲线如图1所示。从图中可以看出，随着循环荷载次数增加，软化指数逐渐减小，土体软化程度逐渐增加，δ-lgN关系曲线表现为线性关系。相同循环次数条件下，动应力越大，软化指数越小，土体软化程度越高，表明提高动应力将会加速土体软化。通过图1(a)中试样X1和X2的比较可以看出，相对于加载波形为正弦波而言，加载波形为半正弦波将会提高土体软化程度。对比图1(b)中试样Y1和Y2可以看出，循环荷载作用下，土体在排水条件软化程度要比不排水条件下的软化程度要高。

图1 土样软化指数曲线

3.2 刚度软化分析

常规三轴试验分析中，黏土的刚度用应力-应变关系曲线中割线剪切模量Gsec的大小来描述。循环荷载作用下，动应力-应变关系曲线表现为一系列封闭的滞回圈，并且随着循环次数的增加而向右移动，累积塑性应变逐渐增加[9]。每一个滞回圈由加载曲线与卸载曲线2部分组成。已有研究成果表明，加载与卸载时割线剪切模量Gsec随循环应变幅值εs变化规律相同，故本文仅以加载曲线为例对饱和黏土和淤泥质黏土进行刚度软化分析。加载曲线中，Gsec定义[10]如下：

(2)

式中：εa为轴向应变；q为偏应力；εamin为加载曲线中应变的最小值。

试样X4在不同循环次数下Gsec-εs关系曲线如图2所示。从图2可以看出，在循环应变初期，Gsec变化幅度很大，定义最大割线剪切模量Gmax对应的循环应变为临界屈服应变εp。当εs<εp时，Gsec随循环应变累积而逐渐增大，试样表现出刚度硬化现象;当εs>εp时，Gsec随循环应变累积而逐渐降低，试样刚度逐渐减小，出现刚度软化现象。因此，可以判断试样在每一循环次数中都存在临界屈服应变εp，王军等[10]通过对饱和软黏土软化现象分析也得到了相似的结果。

图2 Gsec-εs关系曲线(试样X4)

对于珠海粉质黏土，从图2(a)中可以发现，临界屈服应变εp大致范围在循环应变0.02%～0.05%，且随着循环次数的增加，εp逐渐增大。每一循环中，割线剪切模量Gsec随εs累积，初期时变化幅度较大，说明软化速率较快，之后随着εs的逐渐增大，Gsec变化幅度减小，逐渐趋于平缓，说明软化速率逐渐减慢。通过对比不同循环次数内的曲线，可以看出，当εs大于某一值时，曲线重合，Gsec趋于一致，说明此时循环次数对Gsec影响很小。

从图2中还可以看出：①循环次数很低时，Gsec从最大值到最小值衰减幅度较大，如N=6时衰减幅度为13 MPa。循环次数很高时，Gsec从最大值到最小值衰减幅度较小，如N=20 961和N=73 961时衰减幅度分别为6 MPa和4 MPa，表明土体刚度软化现象逐渐减弱。②当循环次数大于20 000次时，Gsec-εs曲线从循环应变发展初期就基本重合，说明循环次数对刚度软化影响已很小。

图3为试样X4的Gmax-N关系曲线。从图3可以看出，随循环次数N增加，Gmax减少。在100次循环次数以内，循环次数对Gmax的影响较大，Gmax发生较大幅度的衰减，衰减幅度达到5.2 MPa。随循环次数N增加，循环次数对Gmax的影响减弱，从2001次至73 961次的7万余次循环中，Gmax的衰减幅度仅为3.8 MPa。

图3 Gmax-N关系曲线

淤泥质黏土试样Y2的Gsec-εs关系曲线如图4所示。通过试验发现，循环次数较低时，εp随循环次数增加而增加，临界屈服应变εp大致范围位于循环应变0.03%～0.05%。随εs逐渐增大，Gsec变化幅度趋于平缓，集中于某一条直线上，循环次数的影响不明显。

图4 Gsec-εs关系曲线(试样Y2)

从图4(b)中可以看出，当循环次数大于2 000时，随εs逐渐增大，由于土体孔压已趋于稳定，曲线趋于一条水平直线，试样基本不发生刚度软化。另外通过对比不同排水条件下刚度软化曲线(见图5)可以看出，排水条件能够影响土体循环荷载下的刚度软化，土体在排水条件下要比不排水条件下刚度软化程度高。

图5 不同排水条件下Gsec-εs关系曲线

不同动应力条件下土体刚度软化的情况如图6所示。可以看出，相同循环次数下，动应力越大，Gsec越小，土体软化程度越高，进一步说明动应力对土体刚度软化有较明显的影响。另外，临界屈服应变εp随着动应力的增加而逐渐变大。

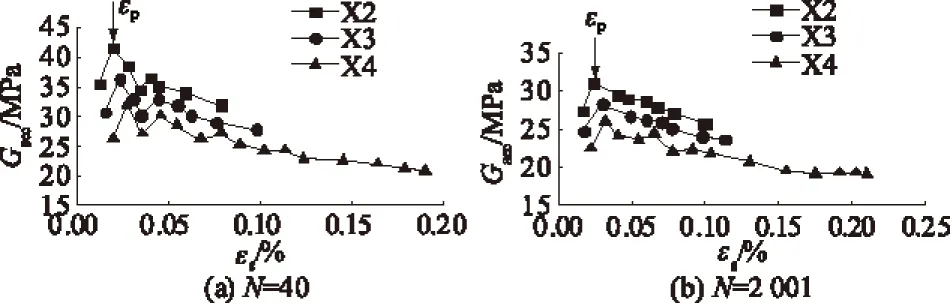
图6 不同动应力下Gsec-εs关系曲线

4 结 论

(1) 在循环应变初期，Gsec变化幅度很大，试样在每一循环次数中都存在临界屈服应变εp:当εs<εp时，Gsec随循环应变累积而逐渐增大，试样表现出刚度硬化现象;当εs>εp时，Gsec随循环应变累积而逐渐降低，试样刚度逐渐减小，出现刚度软化现象。

(2) 循环次数较低时，土体刚度软化现象明显，但当εs发展到某一值时，Gsec-εs关系曲线重合，循环次数影响不明显；对粉质黏土，当循环次数很高时，土体刚度软化程度降低，且Gsec-εs曲线从循环应变发展初期就基本重合，集中于某一条曲线；对淤泥质黏土，当循环次数很高时，Gsec-εs曲线趋于一条水平直线，试样基本不发生刚度软化。另外，加载波形会影响土体的刚度软化程度。

(3) 相同循环次数条件下，动应力越大，软化指数越小，土体软化程度越高；土体在排水条件下软化程度要比不排水条件下软化程度要高。

参考文献：

[1] 周 建，龚晓南. 循环荷载作用下饱和软黏土应变软化研究[J]. 土木工程学报, 2000, 33(5): 62-68. (ZHOU Jian, GONG Xiao-nan. Study on Strain Softening in Saturated Soft Clay under Cyclic Loading[J]. China Civil Engineering Journal, 2000, 33(5): 62-68. (in Chinese))

[2] VUCETIC M, DOBRY R. Degradation of Marine Clays under Cyclic Loading[J]. Journal of Geotechnical Engineering, 1988,114(2):133-149.

[3] LEFEBVRE G, PFENDLER P. Strain Rate and Preshear Effects in Cyclic Resistance of Soft Clay[J]. Journal of Geotechnical Engineering, 1996, 122(1): 21-26.

[4] IDRISS I M, DOBR Y R, SINGH R D. Nonlinear Behavior of Soft Clays during Cyclic Loading[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1978, 104(12): 1427-1447.

[5] YASUHARA Y, HYDE A F L, TOYATA N,etal. Cyclic Stiffness of Plastic Silt with an Initial Drained Shear Stress[C]∥Proceedings of Geotechnique Symposium in Print (SIP) on Prefailure Deformation Behavior, London,January 1,1998: 371-382.

[6] 要明伦，聂栓林. 饱和软黏土动变形计算的一种模式[J]. 水利学报，1994，(7)：51-55.(YAO Ming-lun, NIE Shuan-lin. A Model for Calculating Deformation of Saturated Soft Clay[J]. Journal of Hydraulic Engineering, 1994, (7): 51-55.(in Chinese))

[7] 王 军，蔡袁强，潘林有. 双向激振下饱和软黏土应变软化现象试验研究[J]. 岩土工程学报，2009,31(2)：178-185.(WANG Jun, CAI Yuan-qiang, PAN Lin-you. Degradation of Stiffness of Soft Clay under Bidirectional Cyclic Loading[J]. Chinese Journal of Geotechnical Engineering, 2009,31(2)：178-185. (in Chinese))

[8] HYODO M,YASUHARA K. Analytical Procedure for Evaluating Pore-water Pressure and Deformation of Saturated Clay Ground Subjected to Traffic Loads[C]∥Proceedings of the 6th International Conference on Numerical Methods in Geomechanics. Innsbruck, Austria, April 17-22, 1987:653-658.

[9] KOKUSHO T. Cyclic Triaxial Test on Dynamic Soil Properties for Wide Strain Range[J]. Soils and Foundations, 1980, 20(2): 45-60.

[10] 王 军，蔡袁强，徐长节. 循环荷载作用下软黏土刚度软化特征试验研究[J]. 岩土力学，2007，28(10)：2138-2144. (WANG Jun, CAI Yuan-qiang, XU Chang-jie. Experimental Study on Degradation of Stiffness of Saturated Soft Clay under Undrained Cyclic Loading[J]. Rock and Soil Mechanics, 2007，28(10)：2138-2144. (in Chinese))