考虑拱效应的矩形巷道顶板稳定性

，

(1.辽宁省交通高等专科学校 建筑工程系，沈阳110122; 2.辽宁工程技术大学 土木与交通学院， 辽宁 阜新123000)

1 研究背景

1943年Terzaghi通过著名的活动门试验，证实了由于介质的不均匀移动导致介质应力状态发生改变，引起了应力重新分配，形成拱效应[1]。很多工程问题中均存在拱效应这一现象，一些学者也根据不同的工程特点采用理论、试验和数值等方法研究拱效应特性。如文献[2-4]研究了抗滑桩桩土作用中拱效应的分析，分析了桩后土拱稳定性因素，提出了对抗滑桩设计的一些建议；文献[5-6] 研究了土拱效应对挡墙主土压力非线性分布的影响，并对土压力计算进行相应的改进，为挡土墙的设计提供了一些建议等。

在巷道稳定性方面对于拱效应理论成果的研究，目前见诸报道的较少。伍永平等[7]采用物理相似材料模拟和数值模拟的手段，模拟了在拱效应的作用下大倾角煤层开采时三维应力状态下围岩形成拱壳承载结构，并建立了应力拱壳分析模型，推导出宏观应力拱壳的形态方程，给出应力拱壳的稳定性判别准则；杜晓丽等[8]采用数值模拟及相似物理试验，结合工程实际的手段，研究了采动作用下的岩体应力转移变化时压力拱的演化规律；王滨等[9]从岩溶塌陷临界土洞的极限平衡高度角度研究了土洞顶部压力拱稳定性，并建立了临界土洞极限平衡高度计算公式。

显然拱效应这一现象在很多工程中广泛存在，但现有研究成果对于拱效应力学模型及其分布尚缺乏统一的认识。尤其是在巷道稳定性分析方面，这些研究多是以模拟试验的手段进行研究，研究考虑的均是掘进后围岩自身达到平衡时围岩形成具有拱体力学特性的结构稳定性，而未考虑人工支护(支护强度大小或时机)对该结构的影响。

本文以煤矿矩形巷道为主要研究对象，从研究顶板围岩形成的承载应力拱稳定性角度出发，分析矩形巷道形成后顶板承载应力拱与支护反力之间的相互作用力学特性，分析矩形巷道不同跨距、顶板支护强度、两帮加固岩层厚度、顶板围岩深度等因素对顶板压力拱效应的影响及变化规律，阐明矩形巷道顶板压力拱作用机制；并以摩尔库伦为破坏准则，建立矩形巷道顶板稳定控制方程，并通过工程实例验证其适用性。

2 承载应力拱力学模型

承载应力拱是岩体为抵抗不均匀变形而进行自我调节的一种现象，是围岩内应力发生集中、传递路线发生的偏转而形成的一种拱形应力分布区[10]。矩形巷道掘进完毕，根据力的相互作用原理，两帮直立墙与顶板支护将形成一个与顶板压力相平衡的反作用力。按平面问题考虑，对于两帮等效直立墙A和B与支护C(人为施加的支护)受力情况，建立矩形巷道横断面分析模型如图1所示。

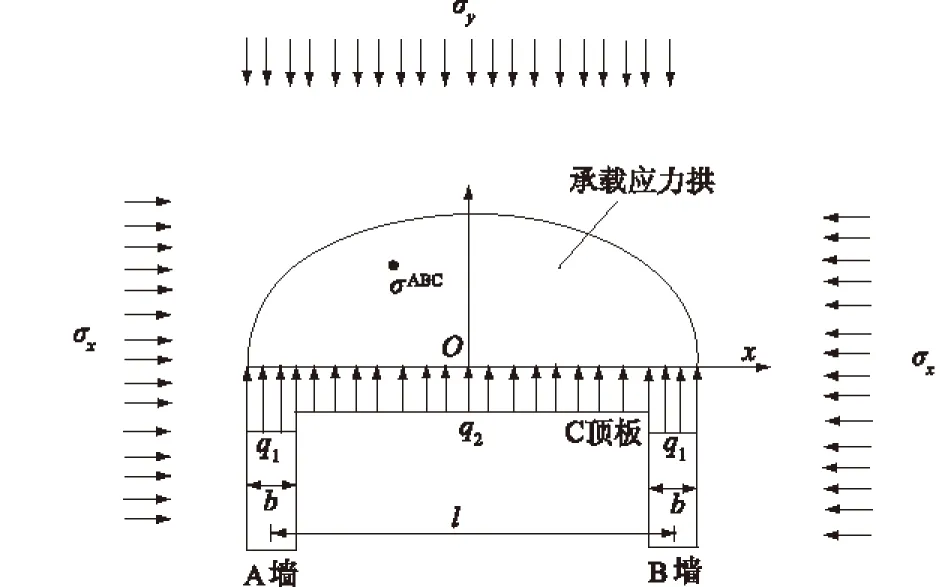
图1 拱效应分析模型

根据力的平衡有如下关系：

2bq1+q2(l-b)=N(b+l) 。

(1)

式中：b为承载应力拱向巷道两帮扩展深度，经两帮围岩加固形成等效直立墙A和B，起拱脚支撑作用，大小由文献[11]方法确定，即b=htan(45°-φ/2)，h为断面高，φ为内摩擦角；q1为A，B墙支反力(MPa)；q2为顶板支护反力(MPa)；l为A，B墙距离(m)；N为顶板压应力(MPa)，可按计算[12]或实测取值。

本文假定：①矩形巷道围岩为均质；②顶板任一点的附加应力只是受到等效直立墙A和B及支护C反力的叠加作用；③两边等效直立墙A和B与支护C反力全部作用在顶板围岩上；④顶板破坏前，两边等效直立墙不发生破坏。

根据弹性力学中Flamant解，推导顶板围岩内任意一点的附加应力，分析附加应力的叠加所形成的应力拱在顶板围岩内分布规律。

A墙作用：

(2)

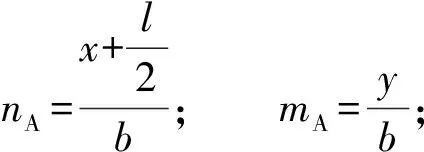
B墙作用：

(3)

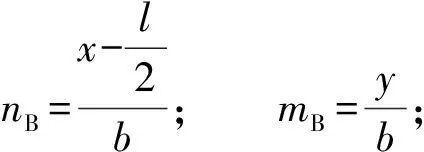
支护C作用：

(4)

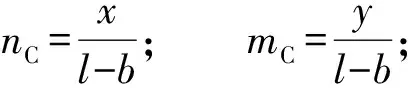
根据图1力学模型对该问题的阐述及假设条件，考虑顶板围岩压力由结构A，B，C三者承担，根据力的叠加原理，y方向上任一点总附加应力σyABC可以表示为

(5)

联立式(2)至式(5)，可得出围岩y方向上任一点的总附加应力表达式：

σyABC=

(6)

3 承载应力拱分布

根据式(6)，赋予式中参数：l=6.0，q2=0.4 MPa,N=0.6 MPa。运用MATLAB7.0，联立式(1)和式(7)，编制程序。在xoy平面内绘制总附加应力σyABC等值线图，观察分布规律如图2所示。

(7)

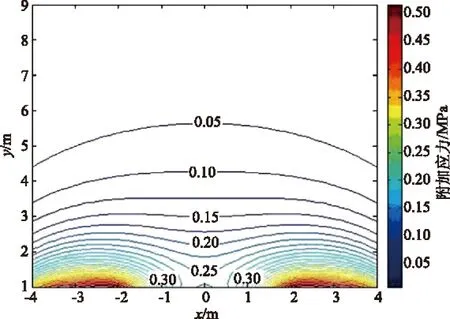
图2 拱应力等值线图

x，y轴分别对应的是顶板和顶板围岩。在x轴上坐标-4～-2与2～4为A墙与B墙q1作用位置，中间-2～2为顶板支护反力q2作用位置。显然，等效直立墙与顶板相互作用处附加应力等值线呈现明显的拱形分布。顶板浅部(y≤2 m)附加应力等值线呈独立卵形拱分布，顶板深度增加(y>2 m)，两独立承载应力拱相互叠加，整体应力状态呈现圆弧拱分布，并将两直墙包裹在拱跨之间。附加应力等值线图关于x=0轴对称，随着围岩深度增加拱应力值逐渐减小。若改变顶板支反力，围岩内部应力分布仍然呈拱形分布状态。由应力等值线分布可以看出，顶板围岩受附加应力为两等效直墙与支反力所提供，当支反力较小时，附加应力主要由A，B两直墙提供；当支反力较大时，则三者共同叠加，在顶板围岩内形成承载应力拱，抵抗顶板围岩的进一步变形。支护反力对总体应力等值线的影响较小，是因为人为提供的支护反力对于顶板应力状态较影响小，一般人类能达到的支护最大在1 MPa左右[13-16]。

围岩性质是影响巷道稳定性中最为重要的因素，最大限度地利用围岩自稳能力是提高巷道稳定性的重要手段。矩形巷道开挖形成围岩应力大于岩体自身强度，则此时围岩应力较大区域开始发生破坏，形成了围岩破裂区及塑性区。该承载应力拱内的岩体承受上覆岩体重量及自重，形成具有拱体力学特性的稳定结构。对于围岩而言，初次开挖未形成承载应力拱时立即进行围岩支护，则会造成支护材料的浪费，若支护较晚，围岩形成的承载应力拱逐渐破坏可能造成围岩变形过大而同样支护效果不好。为了寻求好的支护时机和支护力，需对该顶板形成的承载应力拱力学特性进行分析研究。

4 顶板承载应力拱特性分析

4.1 直墙间距变化与拱效应

其他条件不变，改变l,观察分析(x=0,y=2)拱效应特点。q2支反力分别为0.1，0.2 ，0.3，0.4 MPa时，与l/b对应关系曲线如图3所示。

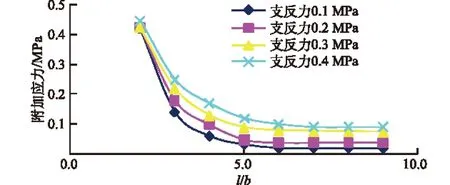
图3 附加应力与l/b关系曲线

间距l较小时，无论采取多大的支护反力，在该点处的总附加应力值均相接近，原因是大部分竖向应力均由两侧直立墙支撑，二者的叠加使承载应力拱内岩体之间压应力较大，可以支撑得住承载应力拱上覆岩体竖向应力作用，承载效果较好；间距l较大时，支护反力大小对承载应力拱的形成影响开始逐渐明显，此时需要较大的支护反力可以达到较好的拱效应支撑作用,间距l继续增大，两侧A，B墙应力的叠加效果减弱，因此较大的支护反力可以使顶板承载应力拱承载效果增加，但为了争取大跨距而提高支护反力往往对于支护设备和技术提出了很高的要求。

支护反力一定时，间距l越近，直立边墙附加应力叠加效果越明显，随着间距的增加2≤l/b≤5时拱效应衰减较快，围岩自身承载能力降低迅速；当l/b>5时，顶板内部附加应力主要为支护反力作用，直立墙A，B附加应力叠加基本为0，而完全由支护反力提供支撑作用。继续拉大间距l，拱效应大幅度消弱，直至消失。拱效应明显时可充分利用围岩形成的应力拱提供的承载力，选择“抗让”结合，而拱效应不明显，则需支护立即抑制住围岩变形。倘若开挖形成破裂区后而未进行及时支护，围岩所形成的承载应力拱将随着时间的增长而逐渐坍塌，但是这种坍塌并不是无限制的，随着应力的重新分布围岩将会重新达到一个稳定状态，形成新的承载应力拱，较原来承载应力拱拱脚外移，拱高增大，向深部扩展。

4.2 顶板围岩深度与承载应力拱效应

根据上述建立的分析模型，取x=0，改变顶板深度距离y，支反力q2及墙间距l，保持等效直立墙宽度b不变。由图2知，x=0对称中心线上，随距离y的增加，围岩中的附加应力先增大，达到峰值后逐渐减小，峰值出现的位置应力拱效应的作用最强[7]。将各个情况下对应的附加应力峰值对应的位置列入表1中。

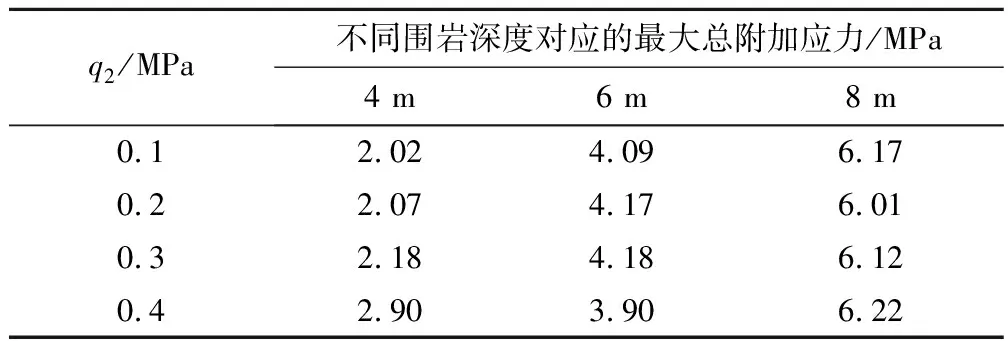
表1 最大总附加应力与围岩深度的关系

经观察，峰值出现的位置正好大约为(x=0,y=l-b)位置处。

4.3 顶板承载应力拱稳定性算法

基于上述对承载应力拱效应分析，进一步研究顶板稳定性问题。由结构力学知，拱形构件拱顶位置是受力破坏的关键点。因此顶板稳定性分析中，选择承载应力拱拱顶为研究对象，随着l的增大，围岩承载应力拱效应将逐渐削弱直至破坏，由表1数据分析知(x=0,y=l-b)处为应力拱拱顶附加应力峰值点，当该点围岩处于极限平衡状态时应满足Mohr-Coulomb破坏准则,见公式(7)。

方程推导：

(x=0,y=l-b)处的剪应力为

(8)

总应力为:

0.552q2+N=σ1;

(9)

0.041q2+Nx=σ3。

(10)

式中：Nx为顶板围岩侧向压力；Nx=k0N，k0为侧压力系数。

将式(9)、式(10)代入式(7)，再利用式(1)消去q1，即可得到关于l，q2，b的隐式方程，f(h,q2,l)=0。可运用matlab求解函数fsolve进行该未知参数的隐函数控制方程求解。

按照上述计算，在已知巷道高度h及设定支护强度情况下，可以求得最大跨距；也可以在已知巷道高度h及所需跨距情况下，求得所需最小的支护强度。

5 工程实例

白羊岭煤矿101工作面开切眼标高+610至+630，地面标高+1 053至+1 167。顶板厚度基本顶为1.36～4.94 m，直接顶为泥岩厚度5.07～11.95 m，无伪顶。工作面开切眼第一次施工的巷道高度为3.8 m，宽度为5.5 m,断面形状近似矩形。k0=0.3,b=1.57 m，N=0.55 MPa,φ=45°，c=0.4 MPa，求得所需支护强度为0.342 MPa。依据所需支护强度计算得出，采取DZ22-30/100型单体液压支柱额定工作阻力的75%，得出单体液压支柱支护密度为1.55根/m2。图4为该巷道其中一个特征断面的内空收敛实测值观测数据，监测表明该断面顶板下沉量较大，而两帮收敛值较小，且二者逐渐趋于稳定值，其他特征断面监测与该断面规律类似，经实测表明该支护强度下巷道稳定性良好。

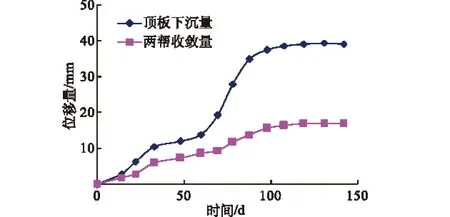
图4 内空收敛实测值

6 结 论

(1) 矩形巷道顶板围岩内应力分布呈现明显的应力拱型分布，顶板浅部内围岩总应力等值线呈独立卵形拱分布，随着顶板围岩深度增加，两独立拱相互叠加，整体应力状态呈现圆弧拱，将两独立墙包裹在拱跨之间。

(2) 间距l较小时，无论采取多大的支护反力，在该点处的总附加应力值均相接近；间距l较大时，支护反力大小对承载应力拱的形成影响开始逐渐明显，此时需要较大的支护反力可以达到较好的拱效应支撑作用,但为了争取大跨距而提高支护反力往往对于支护设备和技术提出了很高的要求。支护反力一定时，间距l越近，直立边墙附加应力叠加效果越明显，随着间距的增加2≤l/b≤5时拱效应衰减较快，围岩自身承载能力降低迅速；当l/b>5时，顶板内部附加应力主要为支护反力作用，直立墙A和B附加应力叠加基本为0，而完全由支护反力提供支撑作用。继续拉大间距l，拱效应大幅度消弱，直至消失。

(3)x=0对称中心线上，随距离y的增加，围岩中的附加应力先增大，达到峰值后逐渐减小，峰值出现的位置应力拱效应的作用最强，峰值出现的位置正好大约为(x=0,y=l-b)位置处。以该点为关键点，基于摩尔库伦强度理论得到了顶板稳定性控制方程。采用数值解法，按照该方程在已知巷道高度h及设定支护强度情况下，可以求得最大跨距；也可以在已知巷道高度h及所需跨距情况下，求得所需最小的支护强度。

参考文献：

[1]TERZAGHI K. Theoretical Soil Mechanics[M]. New York: John Wiley & Son,1943: 66-76.

[2]蒋良潍，黄润秋，蒋忠信.黏性土桩间土拱效应计算与桩间距分析[J].岩土力学，2006,27(3)：445-450. (JIANG Liang-wei, HUANG Run-qiu, JIANG Zhong-xin. Analysis of Soil Arching Effect between Adjacent Piles and Their Spacing in Cohesive Soils[J]. Rock and Soil Mechanics, 2006,27(3)：445-450.(in Chinese))

[3]李邵军，陈 静，练 操.边坡桩-土相互作用的土拱力学模型与桩间距问题[J].岩土力学，2010,31(5)：1352-1358. (LI Shao-jun, CHEN Jing, LIAN Cao. Mechanical Model of Soil Arch for Interaction of Piles and Slope and Problem of Pile Spacing[J]. Rock and Soil Mechanics, 2010,31(5)：1352-1358. (in Chinese))

[4]刘 钦，李地元，刘志祥,等.水平推力作用下抗滑桩间土拱效应影响因素的数值分析[J] 中南大学学报(自然科学版)，2011，4(7)：2071-2077. (LIU Qin, LI Di-yuan, LIU Zhi-xiang,etal. Numerical Analysis of Influence Factors on Soil Arching Effect between Anti-sliding Piles under Horizontal Pushing Loads[J]. Journal of Central South University (Science and Technology), 2011，4(7)：2071-2077.(in Chinese))

[5]彭述权，李夕兵，樊 玲. 刚性挡墙主动破坏墙后土拱效应细观研究[J]. 中南大学学报(自然科学版)，2011,42(4)：1099-1104.(PENG Shu-quan, LI Xi-bing, FAN Ling. Meso-scale of Soil Arching for Rigid Retaining Wall Active Failure[J]. Journal of Central South University (Science and Technology), 2011,42(4)：1099-1104. (in Chinese))

[6]吴 明，彭建兵，徐 平,等. 考虑土拱效应的挡墙后土压力研究[J].工程力学，2011,28(11)：89-95.(WU Ming, PENG Jian-bing, XU Ping,etal. Study on Earth Pressure against Rigid Retaining Walls Considering Soil Arching Effects[J]. Engineering Mechanics, 2011,28(11)：89-95. (in Chinese))

[7]伍永平，王红伟，解盘石,等.大倾角煤层长壁开采围岩宏观应力拱壳分析[J].煤炭学报,2012,34(14):559-564. (WU Yong-ping，WANG Hong-wei，XIE Pan-shi,etal. Analysis of Surrounding Rock Macro-stress Arch-shell of Longwall Face in Steeply Dipping Seam Mining[J]. Journal of China Coal Society, 2012,34(14):559-564. (in Chinese))

[8] 杜晓丽.采矿岩石压力拱演化规律及其应用的研究[D].徐州：中国矿业大学，2011.(DU Xiao-li. Research on the Evolution and Its Application of Rock Pressure Arch in Coal Mining[D]. Xuzhou: China University of Mining and Technology, 2011. (in Chinese))

[9] 王 滨，贺可强.岩溶塌陷临界土洞的极限平衡高度公式[J].岩土力学，2006,27(3)：458-462.(WANG Bin, HE Ke-qiang. Study on Limit Equilibrium Height Expression of Critical Soil Cave of Karst Collapse[J]. Rock and Soil Mechanics, 2006,27(3)：458-462. (in Chinese))

[10] SONG Hong-wei, ZHAO Jian, WANG Chuang. Study on Concept and Characteristics of Stress Rock Arch Around a Cavern Underground[C]∥Tunnelling and Underground Construction Society (Singapore). Proceedings of Underground Singapore 2003 and Workshop Updating the Engineering Geology of Singapore, November 27-28, Singapore, 2003: 44-51.

[11] 魏锦平,郜进海,陈商强.基于梁-拱式组合结构的薄层状复合顶板锚固设计[J] 采矿与安全工程学报,2009,26(4):499-502. (WEI Jin-ping, GAO Jin-hai, CHEN Shang-qiang. Anchoring Design for Thin-Layered Composite Roof Based on Beam-Arch Compound Structure[J]. Journal of Mining & Safety Engineering, 2009,26(4):499-502. (in Chinese))

[12] 张荣立.采矿工程设计手册[M].北京：煤炭工业出版社，2003.(ZHANG Rong-li. Manual of Mining Engineering Design [M]. Beijing: China Coal Industry Publishing House, 2003. (in Chinese))

[13] 侯公羽，李晶晶，裘 彬,等.恒载作用下轴对称圆巷围岩的流变变形方程求解[J]岩土力学，2011,32(2)：341-346. (HOU Gong-yu, LI Jing-jing, QIU Bin,etal. Solving Equation of Rheological Deformation in Axisymmetric Round Well under Dead Load[J]. Rock and Soil Mechanics, 2011,32(2)：341-346. (in Chinese))

[14]王同旭,麻洪蕊.巷道支护力作用及影响因素分析[J].山东科技大学学报(自然科学版),2009,28(4):40-42. (WANG Tong-xu, MA Hong-rui. The Effect of Roadway Supporting Forces and Analysis of Its Influence Factors[J]. Journal of Shandong University of Science and Technology(Natural Science)，2009,28(4):40-42. (in Chinese))

[15]杨 超,陆士良,姜耀东.支护阻力对不同岩性围岩变形的控制作用[J].中国矿业大学学报, 2000,29(2):170-173. (YANG Chao, LU Shi-liang, JIANG Yao-dong. Controlling Effects of Support Resistance on Roadway Deformation under Different Rock Conditions[J]. Journal of China University of Mining & Technology, 2000,29(2):170-173. (in Chinese))

[16]柏建彪,侯朝炯.深部巷道围岩控制原理与应用研究[J].中国矿业大学学报,2006,35(2):145-148. (BAI Jian-biao, HOU Chao-jiong. Control Principle of Surrounding Rocks in Deep Roadway and Its Application[J]. Journal of China University of Mining & Technology,2006,35(2):145-148. (in Chinese))