基于有限元法的土石坝施工填筑数值仿真及位移修正方法探讨
2014-08-16,,,
, ,,
(三峡大学 a.水利与环境学院; b.土木与建筑学院,湖北 宜昌 443002)
1 研究背景
有限单元法在土石坝的应力应变分析中得到了广泛的应用[1],同时也为国内外重大工程的建设提供了理论指导[2-5]。由于土体的应力应变关系具有明显的非线性特性[6],在进行土石坝的有限元分析中一般采用增量法来对施工全过程进行仿真分析,这种方式不仅能反映出施工过程中各阶段的应力应变情况,而且能模拟土石坝的施工填筑及蓄水运行的全过程。
采用有限单元法对土石坝施工填筑过程进行数值仿真时,整个分析对象(坝体、地基等)的计算网格是一次性建成的,根据实际工程中坝体分区施工次序来对施工单元和未施工单元进行不同处理,从而达到施工过程的模拟。大型商用软件往往采用生死单元的方式[7-8],通过控制单元的施工(激活)并一次性施加自重荷载来进行施工过程的模拟,这种处理方式的计算效率不高,而且在激活施工单元时需要对其位移进行处理,应该说不是一种最佳的施工填筑模拟方法。
同时,在土石坝施工填筑仿真模拟中,考虑到坝体高度、仿真精度及计算效率的因素,计算模拟的施工填筑不可能按照实际填筑层来模拟,往往将几个实际填筑层合并成一个计算填筑层,整个坝体分为十几个或几十个填筑层来进行模拟。而在采用有限单元法对施工填筑级进行模拟时,施工填筑单元的自重荷载是一次性施加的,而实际施工时填筑级是一层层碾压逐级加载的,这2种方式下土坝的变形机理是不同的。在不考虑土体固结等时间因素对变形影响的前提下(即假定新填筑层的变形在施工过程中瞬时完成),已填筑层的自重不影响其上部未施工土层的变形。填筑层内某一点土体的变形来自于该点上方土体的压力,该点下面的土体重力对其变形没有影响,则每层填筑层顶部位移应该为零。但按照施工填筑单元的自重荷载一次性施加的情况下,填筑层顶部的位移最大,并由此最终得到的累积竖向位移等值线出现不合理的锯齿状分布的现象,这样就导致填筑仿真得到的位移场与实际不一致。针对这一问题,国内外学者[8-11]提出在数值仿真计算位移的基础上乘以修正系数的方法将其改善,但是对修正公式适用性的研究不完善。
本文基于上述研究背景,对有限单元法在土石坝施工填筑数值仿真中的施工填筑过程模拟及填筑位移修正进行了研究,提出了一种对施工仿真单元的处理方式,并对填筑位移修正方法进行了完善。
2 施工填筑中施工单元的处理
基于有限单元法的施工填筑仿真是根据实际工程中坝体分区施工次序来对施工单元和未施工单元进行不同处理,从而达到施工过程的模拟。
目前对于该问题,采用较多的是“生死单元”[7-8]法。在进行施工仿真前,分析模型的有限元网格在一次性准备好的前提下,先对所有单元进行“杀死”,然后根据填筑次序,逐步地对填筑区内的单元进行“激活”,从而达到对施工过程的真实模拟。对于“杀死”的单元,计算程序并不是将这些单元从计算模型中删除,而是将其刚度矩阵乘以一个很小的因子,同时单元的荷载全部变为零;如果单元开始被施工,则单元被重新激活,程序将其刚度恢复,并施加作用于单元上的所有荷载。有些商用软件在重新激活单元时,被激活的单元由于其边界上有非零位移,这时软件会把非零位移作为已知位移条件施加在新激活单元的边界上,这样就产生了刚激活而未施加任何荷载就产生了位移和应力的现象,这显然是不符合实际情况。
国内学者在对大体积混凝土进行施工期温度场仿真时[12],为了对施工过程进行模拟,曾引入“空气单元”的方法来模拟未修建的部分。对于未施工单元,“空气单元”的弹性模量取相邻单元材料弹性模量的1/100~1/1 000,泊松比取0.49,但是对其计算得到的位移不予以累计。单元施工时,将其材料参数恢复,此后开始累积其位移和应力作为计算成果。
“生死单元”法和“空气单元”法作为对施工过程中处理单元的2种模拟方法,其处理方式基本是一样的。从上述2种方法的处理方式可以看出,未施工的单元只是单元刚度矩阵和荷载被赋予很小的值,但仍然参与整个计算过程,施工填筑过程每个荷载步都需要进行包含未施工单元在内的所有单元刚度矩阵的计算和组装,以及求解包含未施工单元自由度在内的所有自由度的平衡方程,乃至随后所有单元的应力计算。这种处理方法在整个施工过程中方程的求解上,方程的总阶数是相同的。但随着计算规模的增大,计算效率将会大大降低。
在某一荷载步内,对于未施工单元,其单元自由度和荷载是不存在的,可以不参与到计算过程中。因此,本文建议的处理方式是:在土石坝施工填筑过程的有限元模拟中,对每个单元赋予1个施工信息或者施工序号,来规划施工过程,并判断单元是否被施工。对于已施工单元,对其自由度进行考虑,对其荷载进行处理,并参与有限元计算;对未施工单元,不考虑其自由度,对其荷载也不用处理,方程求解的阶数只是施工单元的自由度。从计算工作量上讲,这种处理方式不用计算未施工单元的刚度矩阵和应力,不用构建未施工单元的自由度方程;从计算结果来看,由于未施工单元的自由度没有被纳入计算,不管是位移还是应力,均为0,符合实际情况。与“生死单元”法相比,这种处理方式只是在每个荷载步内需要根据单元的施工信息对自由度进行统计,得到自由度指示数组,从计算时间上来看,这个统计工作与未施工单元参与计算过程相比不值一提。因此,从计算效率上来讲,该方法比“生死单元”法有显著的提升。
可粗略地估计这种处理方式对计算效率的提高效果,假定对于线弹性问题,初步假定每个单元的计算分析所占的时间一致,设为t,计算模型共有NE个单元,分NB个荷载步进行计算分析,每个荷载步的施工单元数相同,即NE/NB。对于采用“生死单元”法来处理施工过程,其需要的计算时间为
T1=NE×t×NB。
(1)
采用本文提出的方法来模拟施工过程,其需要的计算时间为
(2)
从上式可以看出,采用本文建议的方法,可节省计算时间接近50%。
为了验证本文提出的施工单元处理方式与“生死单元”在计算效率上的差别,选用某面板堆石坝工程填筑期仿真计算进行算例比较,该工程计算模型节点总数为50 294,单元总数为48 250,填筑期采用52级进行模拟,计算平台为HP Z400工作站 (处理器为至强W3670@3.20G六核)。采用本文提出方法计算时间为28 min,采用“生死单元”的处理方式计算所需时间为50 min,由此可见本文提出的处理方式与“生死单元”法相比,有较高的计算效率,大约可节省50%的计算时间,其与每个荷载步内新施工单元数及每个单元的计算所需时间相关。
3 施工填筑位移修正
在土石坝施工填筑仿真模拟中,往往将整个坝体分若干个填筑层来模拟,每级单元施工时,施工填筑单元的自重荷载是一次性施加的,而实际施工时填筑级是一层层碾压逐级加载的,这2种方式下土坝的变形机理是不同的:自重荷载一次性施加时,竖向某点的沉降为该点下部土层的压缩量,这时顶部位移最大;而实际施工的逐级加载时,竖向某点的沉降为该点以上土重所引起的该点以下土层的压缩量。Clough和Woodward[13]依据一次性加载和逐步加载的机理不同,从理论上推导了2种方式的沉降量,首次提出了在有限元模拟时一次性加载得到计算结果的基础上乘以修正系数的方式来得到逐步多级加载的变形效果。
3.1 单填筑层的位移修正
假定土体为弹性体,考虑体积压缩系数mv为常量情况下,分析一次性加载和逐步加载2种不同作用下竖向位移的理论值。
如图1所示,某一填筑层的高度为h,A点位于坝顶下z深度,A点的沉降是A点以下厚度为h-z的土层AB的压缩量。
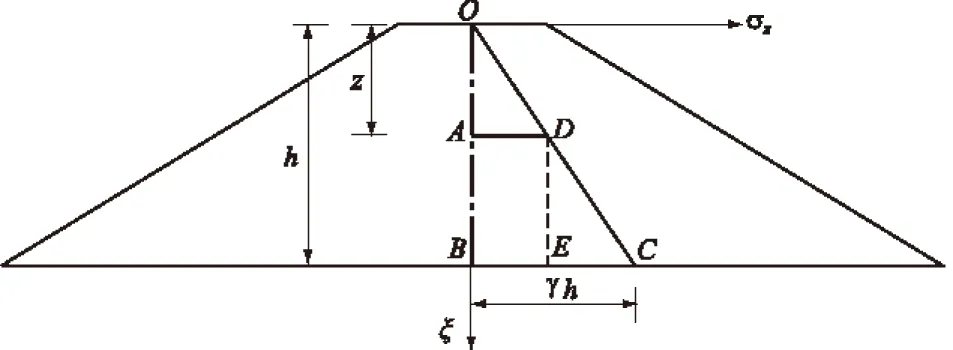
图1 单填筑层坝体竖向沉降受力示意图
一次性加载条件下,引起压缩的应力为自重应力,在压缩层AB内自重应力呈梯形分布,如图1中ABCD所示。根据土体单向压缩沉降理论,一次性加载条件下A点的沉降为
(3)
对逐级加载来说,当填土到A点的高度时,A点以下土体自重所引起的沉降已在填土过程中完成,A点的沉降为零;当填土超过A点的高度时,A点才有沉降。此时,A点的沉降是A点以上土层OA的土重所引起的A以下土层AB的压缩,引起A点沉降的应力在压缩层AB内呈矩形分布,如图1中ABED所示。则逐级加载机理下A点的沉降为
(4)
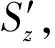
(5)
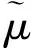
3.2 多填筑层的位移修正
上述修正公式只适用于单填筑层,并不适用于多填筑层情况,而在土石坝施工填筑仿真模拟中,往往将坝体分为十几个或几十个填筑层来进行模拟,如果按照上述公式来修正是会存在一定误差。
在多填筑层下,引起坝顶以下深度为z的某点产生沉降位移不仅仅是在本填筑层会发生沉降,已填筑层均会发生沉降。如图2所示,A点的沉降为新填土层AB的沉降和已填土层BB′的沉降,即可表示为
(6)
式中:z为A点距新填土层顶部O点的深度;h为新填土层的厚度;H为已填筑土层的厚度;σz为引起A点土体沉降的应力。
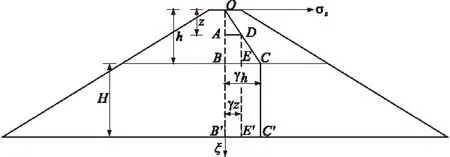
图2 多填筑层坝体竖向沉降受力示意图
一次加载条件下,新填土层AB内引起沉降的压缩应力呈梯形分布,如图中ABCD所示;已填土层 内的压缩应力呈矩形分布,如图中BB′C′C所示。则A点的沉降可表示为
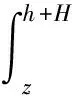
mvγ(h2-z2)/2+mvγhH。
(7)
对逐级加载来说,A点的沉降是A点以上土层OA的土重所引起的A以下土层AB′的压缩,引起A点沉降的应力在压缩层AB′内呈矩形分布,如图2中AB′E′D所示。则逐级加载机理下A点的沉降为
mvγz(h-z)+mvγzH。
(8)
则其修正系数如下式所示:
(9)
从以上分析可以看出,单填筑层中新填土层中某点的沉降只有该点以下土体的沉降,而多填筑层新填土层中某点的沉降包括已填筑土层在该填筑层作用下的沉降和新填土层中该点以下土体的压缩变形2部分,由此,其位移修正公式有所不同。因此,施工填筑位移的修正公式如下:
(10)

表1 坝体填筑材料计算参数
式中:i为填筑级;z为计算沉降点至填筑顶高;h为本级填筑高度;H为已填筑高度;N为总填筑层数。
Clough和Woodward[13]提出的修正公式(如式(5)),只考虑了单填筑层的情况,而未考虑多填筑层时已填筑土层在新填筑土层作用下会产生沉降;而文献[10]在研究位移场修正时,直接针对多填筑层模型来分析,没有区分单填筑层和多填筑层的不同所引起的修正系数的差异。
从上述分析可以看出当已填筑层厚度H=0时,式(5)和式(9)一致,同时当已填筑层较厚时(即h/H→0),式(9)可简化如下:
(11)
为了分析上式简化及考虑多填筑层与否所引起的误差,假定修正系数为β,将式(9)按h/H的不同,绘制修正系数沿填筑层厚度的分布如图3所示。从图中可以看出,当新填土层与已填土层厚度之比越大时(即h/H→∞),多填筑层的修正系数趋于单填筑层的修正系数(β→2z/(h+z));而当已填筑层较厚时(即h/H→0),多填筑层的修正系数β→2z/(h+z)。
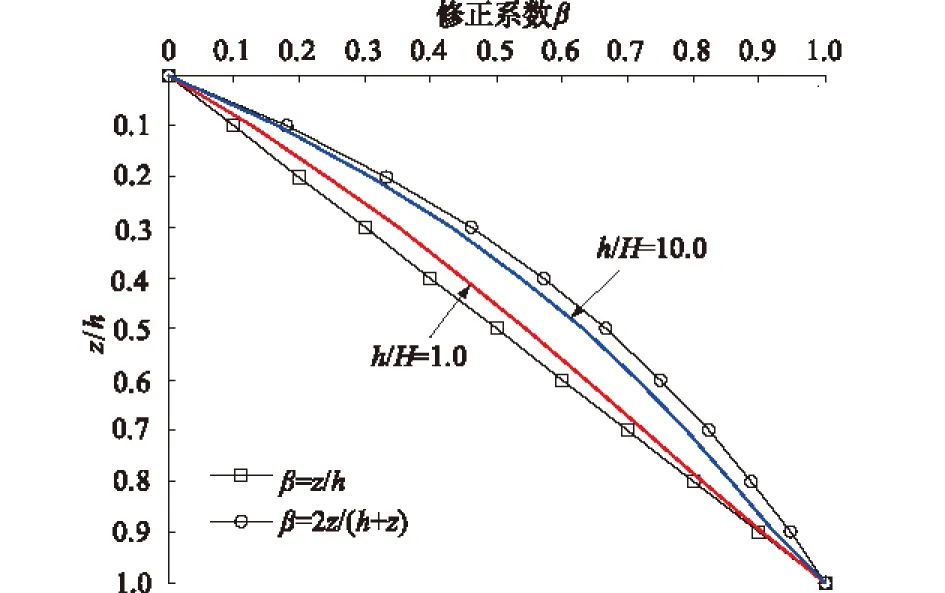
图3 修正系数沿土层深度分布
如果采用式(11)来简化代替式(9),随着填筑层的增加,其误差越来越小,修正系数在第二填筑层时误差最大,在土石坝施工填筑仿真中,考虑到施工强度的因素,填筑层厚较为均匀,即在第二填筑层时,h/H=1.0,此时的简化所引起的最大误差为5%,而且随着填筑层的增加而逐渐减小。
如果不考虑施工填筑层的影响,如文献[10]和[13]所述,采用式(5)或式(11),其最大误差可达到17%,因此在进行位移修正时,需要考虑填筑层的差别,建议在使用有限单元法进行土石坝施工填筑仿真时位移修正系数如下式所示:
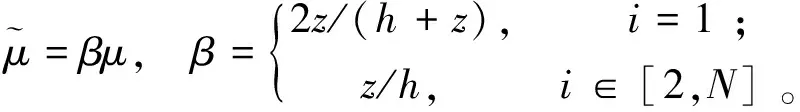
(12)
4 算例应用
选用文献[8]和[10]的算例:一心墙堆石坝,坝高100 m,顶宽10 m,心墙顶宽6 m,坝体上下游坝坡坡比为1∶2.0,心墙坡比为1∶0.2;网格沿坝高分为20层,每层厚度为5 m,坝体和心墙的本构模型采用邓肯E-B模型,材料参数如表1所示,计算网格如图4所示。
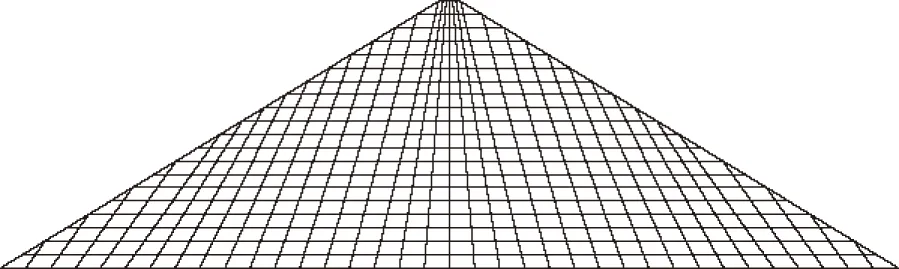
图4 有限元网格图
为了比较位移修正考虑单、多填筑层的差别以及式(12)简化前后的误差,拟定以下5个计算方案:
(1) 施工填筑位移不修正,称为未修正方案。
(2) 根据单填筑层推导出来的修正公式[9,13](式(5)),称为已有修正方案Ⅰ。
(3) 根据多层填筑推导出来的修正公式[10](式(11)),称为已有修正方案Ⅱ。
(4) 考虑填筑层不同的修正公式(式(10)),称为本文修正方案。
(5) 考虑了填筑层不同的简化修正公式(式(12)),称为简化修正方案。
以上5种计算方案的填筑计划均按10级填筑,每级两层单元。
按照上述施工填筑方案得到的竖向位移分布沿坝轴线对称,因而不同修正方案的竖向位移的等值线见图5所示。不同修正方案的位移统计成果见表2所示。
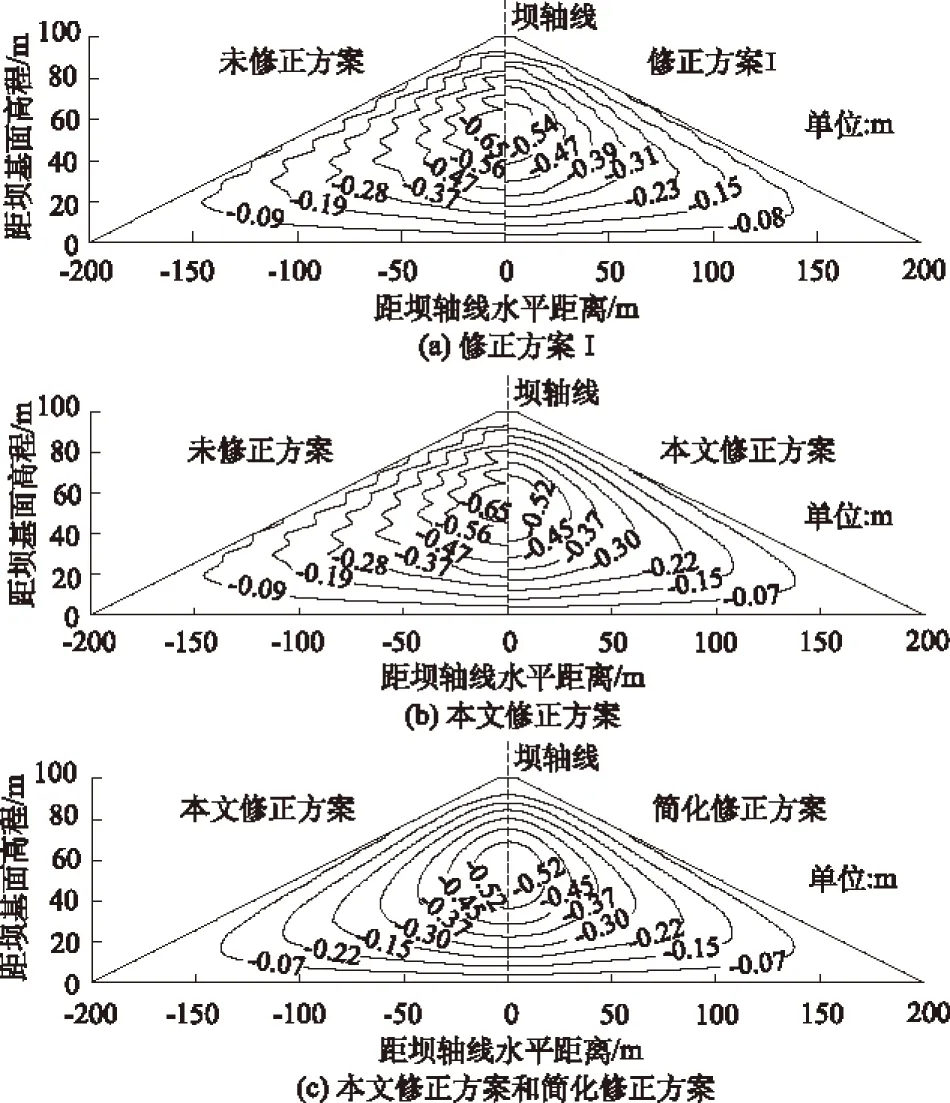
图5 不同修正方案的竖向位移
从未修正方案的竖向位移等值线图可以看出,由于每填筑层的顶部位移不为0,致使累加位移产生如图所示的锯齿状,采用修正方案I修正后,虽有所改善,但由于该方案没有考虑已填筑土层在该填筑层作用下的沉降这一因素,致使修正后的位移图仍有波动性。修正方案Ⅱ、本文修正方案及简化修正方案的修正效果基本一致,如图5(c)所示,这与实际情况较为相符,修正方案Ⅱ虽然没有考虑第一个填筑层的修正系数的不同,但由于后续填筑层中考虑了占绝对权重的已填筑土层在该填筑层作用下的沉降(牵移位移),因此修正效果与本文修正方案相同,只是第一个填筑层内部点的修正沉降位移偏小。

表2 不同方案竖向位移计算结果
从不同方案的计算结果来看,未修正方案的竖向位移最大,达到0.744 m,但由于每填筑层的顶部位移不为0,致使最终坝顶竖向位移达到0.192 m的沉降,这显然不符合实际。修正方案Ⅰ虽然对每个填筑层的顶部位移进行了修正,但没有考虑已填筑土层在该填筑层作用下的沉降,因此修正后竖向位移偏大。修正方案Ⅱ、本文修正方案及简化修正方案的竖向位移基本相同,只是由于由式(9)简化成式(11)后引起较小的差别。
从计算结果和修正后竖向位移等值线分布图来看,由于修正方案II考虑了占绝对权重的已填筑土层在该填筑层作用下的沉降(牵移位移),其计算结果和修正效果均与本文修正方案相同,但从理论上讲,单填筑层和多填筑层的沉降土层不同,其位移修正公式应有所区分,因此本文提出的修正方案及简化修正方案是更为合理。
5 结 论
本文针对有限单元法在土石坝施工填筑数值仿真中的施工填筑仿真模拟及填筑位移修正进行了研究,得到结论如下:
(1) 土石坝施工填筑数值仿真中,建议给每个单元赋予1个施工信息来进行控制,并且未施工单元不参与计算,这种处理方式从计算效率上来讲,比“生死单元”法有显著的提升,可节省计算时间达到50%。
(2) 施工填筑位移修正时,应考虑单填筑级和多填筑级沉降土层的不同,由此对于第一个填筑层与后续填筑层的位移修正公式应有所区分。
(3) 在多填筑层位移修正时,采用β=z/h的简化方式进行处理时,所引起的最大误差为5%,而且随着填筑层的增加而逐渐减小,从修正效果和计算结果来看,这种简化方式是可行的。
参考文献:
[1] 陈慧远.土石坝有限元分析[M].南京:河海大学出版社,1988.(CHEN Hui-yuan. Finite Element Analysis of Earth-Rock Dam[M]. Nanjing: Hohai University Press, 1988. (in Chinese))
[2] 孔宪京,邹德高,徐 斌,等.紫坪铺面板堆石坝三维有限元弹塑性分析[J].水力发电学报,2013,(2):213-222.(KONG Xian-jing, ZOU De-gao, XU Bin,etal. Three-dimensional Finite Element Elasto-plastic Analysis of Zipingpu Concrete Faced Rock-fill Dam [J]. Journal of Hydroelectric Engineering,2013,(2):213-222.(in Chinese))
[3] 潘家军,王观琪,江 凌,等.基于ABAQUS的高混凝土面板堆石坝地震反应三维非线性分析[J].水力发电学报,2011,(6):80-84.(PAN Jia-jun, WANG Guan-qi, JIANG Ling,etal. ABAQUS Three-dimensional Nonlinear Analysis of Seismic Responses of High CFRD [J]. Journal of Hydroelectric Engineering, 2011, (6):80-84. (in Chinese))
[4] 刘萌成,高玉峰,刘汉龙.混凝土面板堆石坝应力变形长期性状有限元模拟[J].岩土力学,2010,31(增1):412-418.(LIU Meng-cheng, GAO Yu-feng, LIU Han-long. Finite Element Analysis of Long-term Stress-deformation Behavior for Concrete-faced Rockfill Dam[J].Rock and Soil Mechanics,2010,31(Sup.1):412-418.(in Chinese))
[5] 杨启贵,常晓林,周创兵,等.水布垭超高面板堆石坝变形控制方法研究[J].岩土力学,2010,31(增2):247-253.(YANG Qi-gui,CHANG Xiao-lin,ZHOU Chuang-bing,etal.Study of Dam Deformation Control Method for Shuibuya High Concrete Faced Rockfill Dam [J].Rock and Soil Mechanics,2010,31(Sup.2):247-253.(in Chinese))
[6] 李广信.高等土力学[M].北京:清华大学出版社,2004.(LI Guang-xin. Advanced Soil Mechanics[M]. Beijing: Tsinghua University Press, 2004. (in Chinese))
[7] 郝文化.ANSYS土木工程应用实例[M].北京:中国水利水电出版社,2005.(HAO Wen-hua. ANSYS Application Examples in Civil Engineering[M]. Beijing: China Water Power Press, 2005. (in Chinese))
[8] 费 康,刘汉龙.ABAQUS 的二次开发及在土石坝静、动力分析中的应用[J].岩土力学,2010,31(3):881-890.(FEI Kang, LIU Han-long. Secondary Development of ABAQUS and Its Application to Static and Dynamic Analysis of Earth-rockfill Dam[J]. Rock and Soil Mechanics,2010,31(3):881-890. (in Chinese))
[9] 殷宗泽.土工原理[M].北京:中国水利水电出版社,2007.(YIN Zong-ze. Earthwork Principle[M]. Beijing: China Water Power Press, 2007. (in Chinese))
[10] 杜 斌,吴梦喜.土石坝分层填筑位移场修正的一种新方法[J].力学与实践,2011,33(4):23-28. (DU Bin, WU Meng-xi. A New Approach for Modification of Displacement in Incremental Construction Analysis of Earth-rock Dam[J]. Mechanics in Engineering, 2011,33(4):23-28. (in Chinese))
[11] 王敏强,聂向珍.土(堆)石坝施工过程位移场有限元仿真分析[J].武汉大学学报(工学版),2003,36(2):74-78. (WANG Min-qiang, NIE Xiang-zhen. Displacement Simulation of Earth-rock Dam in Construction Process by Finite Element Method[J]. Engineering Journal of Wuhan University,2003,36(2):74-78. (in Chinese))
[12] 刘德富,黄达海,田 斌.拱坝封拱温度场及温控优化[M].北京:中国水利水电出版社,2008.(LIU De-fu, HUANG Da-hai, TIAN Bin. Optimization of Joint Closure Temperature Field and Temperature Control Measures for Arch Dam[M]. Beijing: China Water Power Press, 2008. (in Chinese))
[13] CLOUGH R W, WOODWARD R J. Analysis of Embankment Stress and Deformations[J]. Journal of the Soil Mechanics and Foundation Division, ASCE,1967,93(SM4):529-549.
