一种用于三维滑坡模型试验数据处理的新方法

，

(三峡大学 土木与建筑学院，湖北 宜昌 443002)

1 研究背景

三维滑坡模型试验是在三维滑坡试验平台的基础上，根据其原型，按照相似理论确定的相似判据建立三维物理模型，并施加相应的工程荷载，开展一系列试验，从而研究滑坡的破坏机制及形成机制，指导滑坡的防治与预测预报[1]。在三维滑坡模型试验数据的采集、传输和转换过程中，由于试验数据采集系统内部和外部干扰、噪声等的影响，使得系统采集到的数据发生突变，偏离其真实数值。所有这些非正常数据统称为奇异数据，这些奇异数据的存在，将会对数据分析形成干扰。因此必须对采集数据进行处理，使试验数据尽可能地接近其真实值，以提高数据的可靠性和真实性。

目前，在试验监测数据处理中常用的奇异值剔除方法有：目测法；均方值法；一阶差分或二阶差分；小波变换等[2-5]。前3种方法主要是在时间域对信号进行判断和处理，在处理奇异监测数据少、曲线相对平滑、奇异数据突出时，有一定的优势，但是当监测数据较多，毛刺现象明显时,利用上述方法就可能在剔除奇异数据的同时，也删除了一些有用数据。小波变换法是同时对信号进行时域和频域分析，但是在用小波去噪的过程中，小波函数以及其他参数的选择，对去噪效果影响显著，数据处理结果随机性较大。

本文针对三维滑坡模型试验数据特点，利用3σ准则对奇异数据进行检测，对于检测到的奇异数据再利用时间序列分析法对奇异时刻的数值进行预测，用预测值代替奇异值，并给出误差分析，最后利用五点三次平滑法对整个观测曲线进行平滑处理。

2 奇异数据的检测与处理

2.1 奇异数据的检测

三维滑坡模型试验过程中，在滑坡发生失稳破坏之前，当试验数据在采集时间间隔较短时，我们所采集到的各物理量总是平滑连续变化的。比如滑坡体内某部分的体积含水率，如图1所示，体积含水率不可能在前一个时刻为22.9%，在很短的下一个时刻就变为20.87%，而在连续采集的下一个时刻又变回到22.8%。因此，所采集的数据应落在这条曲线两侧的附近，相邻两数据的差值应在某一范围内。3σ准则给出的这个限制区域是[-3σ，3σ]，超出这一范围的即认为是奇异数据。

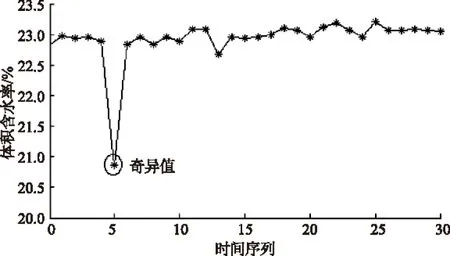
图1 体积含水率曲线中的奇异数据

3σ准则表述如下[6]：

对于观测数据序列{x1,x2,…,xN} ，描述该序列数据的变化特征为

dj=2xj-(xj+1+xj-1)，j=2,3,…,N。

(1)

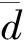
(2)

(3)

根据dj偏差的绝对值与均方差的比值

(4)

当qj>3时，则认为xj是奇异值。

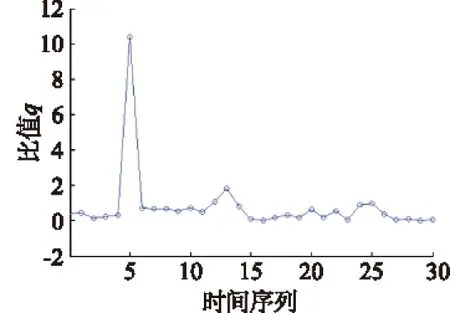
图2 偏差的绝对值与均方差的比值

用上述方法对图1所示的体积含水率曲线进行奇异数据检测，发现在奇异数据存在时刻q的值明显大于3，而其他时刻q的值均较小，如图2所示。这说明用3σ准则对采集数据进行检测是可行的，能有效检测出奇异数据出现的时刻。

2.2 奇异数据的替换

对于检测到的奇异数据，在三维模型试验数据中不能进行简单的剔除处理，因为如果将某一物理量某一时刻的奇异数据剔除，将会产生观测数据序列的“断链”，不利于与其他物理量进行对比分析，所以本文采用时间序列分析法对奇异数据发生的时刻进行预测，用预测数据代替奇异数据，这样就保证了不同物理量的采集数据序列大小一致，便于后期的数据分析。

时间序列预测技术就是通过对预测目标自身时间序列的处理，来研究其变化趋势。时间序列分析中的自适应滤波法是以时间序列的历史观测值进行某种加权平均来预测的，它要寻找一组“最佳”的权数，其办法是先用一组给定的权数来计算一个预测值，然后计算预测误差，再根据预测误差调整权数以减少误差。这样反复进行，直至找出一组“最佳”权数，使误差减少到最低限度。由于这种调整权数的过程与通讯工程中的传输噪声过滤过程极为接近，故称为自适应滤波法。

自适应滤波法的基本预测公式为

(5)

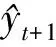
其调整权数的公式为

(6)

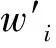
图3是采用时间序列中的自适应滤波法对三维滑坡模型试验某一时间段所采集的体积含水率数据进行预测，并与采用一阶差分的预测数据相比较。由图中的预测曲线和误差曲线可以看出，自适应滤波法预测数据的误差比一阶差分小，且均小于0.01，可以满足替代奇异数据的精度要求。

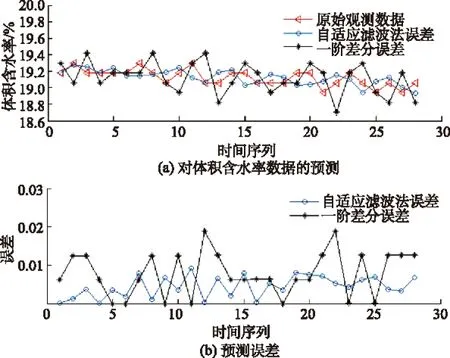
图3 自适应滤波法预测与一阶差分预测对比

3 模型试验采集数据的平滑处理

在三维滑坡模型试验中，利用土压力、孔隙水压力、体积含水率和位移等传感器监测应力场、渗流场和位移场的变化特征。试验数据的采集、传输和转换过程中，由于试验数据采集系统内部和外部干扰、噪声等的影响，使得系统采集到的数据发生突变或波动，减弱了数据变化的规律性。鉴于此，本文采用数据处理技术对受到干扰的数据进行奇异值检测，并用时间序列中的自适应滤波法对出现奇异值的时刻进行预测，用预测值替换奇异值。

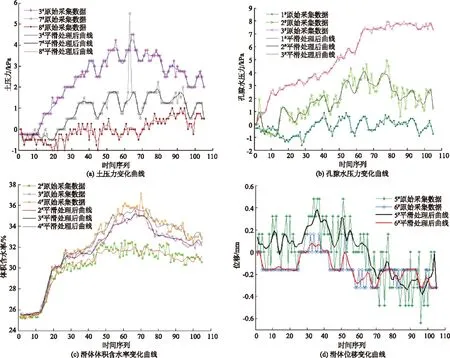
图5 各采集数据变化曲线平滑处理前后对比

图4 试验数据处理流程图

对试验采集数据进行奇异数据检测和替换可以有效去除奇异数据，但是采集数据中还存在其他受干扰的数据，即含有噪声数据，但这些数据又偏离真实值不大，构不成奇异数据，仅表现为毛刺状，使数据不够平滑。对于那些受噪声干扰较弱，只表现为小幅度波动的数据，本文采用五点三次平滑法进行平滑处理，消除噪声的影响，具体处理过程见图4。

五点三次平滑法是局部平滑法的一种，是利用最小二乘法原理对离散数据进行三次最小二乘多项式平滑的方法。五点三次平滑法计算公式为[7]

(7)

式中i=2,3,…,N-2。

4 数据处理结果分析

利用上述方法对三维滑坡模型试验某一工况采集到的土压力、孔隙水压力、体积含水率和位移等含噪声数据进行奇异值检测、替换以及数据的平滑处理。在这个过程中，很好地保留了模型试验本身的真实数据，为后续研究提供了可靠和高质量的分析数据。具体数据处理结果见图5。

从图5(a)可以看出7#土压力传感器采集的数据存在奇异值，利用上述“3σ准则”成功地检测出了奇异数据，并用预测值予以替换，替换后的曲线表现出很好的连续性。证明了上述方法对三维滑坡模型试验采集数据的奇异值处理是有效性和可行性。

从图5(b)和图5(c)可以看出采集数据存在噪声干扰，出现毛刺现象，利用五点三次平滑法可以有效消除由于噪声信号产生的数据波动，处理后的数据很好地保持了原始数据的变化趋势，说明该平滑法对该类数据的处理有一定的优势，取得了很好的效果。

从图5(d)可以看出，位移传感器采集的数据总体变化幅度不大，范围在[-0.6,0.6]之间，由于信号较弱，又存在噪声干扰，使数据表现得极不稳定，使用五点三次平滑法进行平滑处理后的数据也出现了波动现象，但是却显现了数据的总体变化趋势。这从另一个方面也说明了五点三次平滑法不会偏离原始数据的正常变化趋势，只是去除了噪声信号的干扰，使曲线变得光滑。

5 结 论

三维滑坡模型试验是采用模拟试验的手段来研究滑坡形成机制和诱发机制，试验数据的采集和处理的准确性关系到研究成果的可靠性，而在实际试验过程中，由于各种因素的干扰，所采集的数据由于含有噪声信号的影响出现突变或波动。针对这一情况，本文做了以下研究：

(1) 利用“3σ准则”对奇异数据进行检测，检测结果表明该方法可以准确检测出奇异数据出现的时刻，对于那些受噪声干扰较弱的则不检测为奇异数据，有效地保证了原始数据的变化趋势不会因为替换奇异数据而发生变化。

(2) 应用时间序列中的自适应滤波法对检测出奇异数据的时刻进行预测，用预测值替换奇异值，并把自适应滤波法预测与一阶差分预测做了简单的对比。试验结果显示自适应滤波法预测误差明显小于一阶差分法，预测值比较接近真实值。

(3) 对于受噪声信号干扰，表现为小幅度波动的数据，应用五点三次平滑法进行平滑处理，处理结果显示该方法可以有效去除噪声干扰，同时不影响原始数据的变化趋势。

(4) 以上结果显示，本文采用“3σ准则”检测，自适应滤波法预测替换，五点三次平滑法进行平滑处理相结合的预处理技术在三维滑坡模型试验数据处理中是有效的，能够有效去除数据的突变和波动，并保留了原始数据的正常变化趋势。

参考文献：

[1] 罗先启, 葛修润. 滑坡模型试验理论及应用[M].北京:中国水利水电出版社,2008. (LUO Xian-qi, GE Xiu-run. Landslide Model Test Theory and Application[M]. Beijing: China Water Power Press, 2008. (in Chinese))

[2] 马明建. 数据采集与处理技术(第二版)[M]. 西安:西安交通大学出版社,2005. (MA Ming-jian. Data Acquisition and Processing (Second Edition) [M]. Xi’an: Xi’an Jiaotong University Press, 2005. (in Chinese))

[3] 谷阳阳, 赵圣占. 遥测数据野值剔除方法的对比与分析[J]. 战术导弹技术,2012,(2):60-63. (GU Yang-yang, ZHAO Sheng-zhan. Comparison & Analysis on Method of Picking out the Error for Telemetry Data [J]. Tactical Missile Technology, 2012, (2): 60-63. (in Chinese))

[4] 王 楠, 律方成. 基于小波奇异性检测的在线监测数据处理[J]. 电工技术学报,2003,(4):61-64. (WANG Nan, LV Fang-cheng. On-line Monitoring Data Processing Based on Wavelet Singularity Detection[J]. Transactions of China Electro Technical Society, 2003, (4): 61-64. (in Chinese))

[5] 梁桂兰, 徐卫亚, 谈小龙，等. 岩石高边坡安全监测数据的小波变换去噪处理[J]. 岩石力学与工程学报,2008,27(9):1837-1844. (LIANG Gui-lan, XU Wei-ya, TAN Xiao-long，etal. Denoising Processing of Safety Monitoring Data for High Rock Slope Based on Wavelet Transform[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(9): 1837-1844. (in Chinese))

[6] 黄声享, 尹 晖, 蒋 征. 变形监测数据处理(第二版)[M]. 武汉:武汉大学出版社, 2010. (HUANG Sheng-xiang, YIN Hui, JIANG Zheng. Processing of Deformation Monitoring Data (Second Edition)[M]. Wuhan: Wuhan University Press, 2010. (in Chinese))

[7] 陈荣盛,区仕豪. 观测数据的平滑及中心化处理[J]. 舰船科学技术,1982,(6):19-26. (CHEN Rong-sheng, QU Shi-hao. Observational Data Smoothing and Treatment Center[J]. Ship Science and Technology, 1982,(6):19-26. (in Chinese))