汽车空调旋叶式压缩机排气阀片的振动特性

李春银， 王树林

(1.上海理工大学 能源与动力工程学院,上海 200093；2.上海理工大学 材料科学与工程学院,上海 200093)

汽车空调旋叶式压缩机排气阀片的振动特性

李春银1， 王树林2

(1.上海理工大学 能源与动力工程学院,上海 200093；2.上海理工大学 材料科学与工程学院,上海 200093)

排气阀片是汽车空调旋叶式压缩机中的关键零件,是压缩机主要振动噪声源之一。通过对排气阀片结构运动分析，建立了阀片振动的数学模型，并求解了压缩机排气阀片的固有频率及强迫振动。利用UG NX Nastran模态计算，确定了排气阀片的固有频率和振型。测试结果证明，压缩机的外壳振动总加速度、噪声和排气脉动都低于美国通用汽车公司“GMW标准”的规定上限，证明排气阀片工作的工作状态是可靠的。但研究结果表明，阀片振动的极限位移同限位板高度比较接近，因此，提高限位板的高度或者限制阀片的振幅以进一步控制系统的排气脉动和噪声仍然具有一定的空间。分析结果对排气阀片乃至压缩机整体的振动分析与控制以及故障诊断具有参考价值。

旋叶式压缩机；空调压缩机；排气阀片；振动与噪声控制；模态分析

旋叶式压缩机在汽车空调系统中广泛使用，约占当今各类汽车空调压缩机市场份额的10%，它具有低成本、小尺寸、高性能(节能性)、低能耗, 高可靠性等优点。特别是结构简单，转速高, 效率高的特点在小排量汽车中具有明显优势[1-2]，因而应用前景广阔。

排气阀片是旋叶式压缩机中的关键零件之一，它一直处在高频激振、交变高载、高温下运动，排气阀片的性能优良直接影响到压缩机的制冷性能[3]，同时它是压缩机主要振动噪声源之一[4]。研究压缩机排气阀片的振动特性对控制排气阀片振动、降低压缩机排气脉动、减轻压缩机噪声、优化排气阀片设计、提高压缩机可靠性等都具有重要的实际意义。

本文对旋叶式汽车空调压缩机排气阀片的运动进行了分析，建立了阀片振动数学模型，求出了其固有频率和瞬时位移，分析了影响振动的主要因素。利用有限元分析软件UG NX Nastran，对排气阀片进行模态分析，得到了其前5阶固有频率和主振型。通过对压缩机振动加速度、噪声和排气脉动的测试，讨论了排气阀片运动的可靠性。

1 排气阀片结构及运动分析

汽车空调旋叶式压缩机排气阀采用簧片阀，其一端固定在阀座上,另一端处于自由状态，阀座上方安装有限位板，防止阀片在开启过程中出现过冲现象。排量为100 cm3/r的双腔旋叶式压缩机的排气阀片为双簧片，如图1所示。排气阀安装结构如图2(a)，图2(b)为汽缸体(阀座)、限位板、排气阀片(在限位板的下方)、固定螺钉的实物安装结构。

图1 排气阀片实物Fig.1 Material object of the discharge valve

图2 排气阀安装结构Fig.2 Installation of the structure of the discharge valve

随着压缩机旋转，排气阀片随排气腔内气体压力变化而自动地、周期性地完成开启与关闭功能。当排气腔的内外压差足以克服排气阀片弹簧力，阀片开启。随着阀片的开启，阀片挠度加速增大,在惯性力作用下撞向限位板，因冲击能量不能被全部吸收，出现阀片反弹现象，但快速衰减。当排气阀挠度达到一特定值时，前端贴合限位板，后端卷绕限位板作振动。随着主轴转动，前一个排气结束，腔内的压力迅速下降,在阀片自身弹簧力的作用下，排气口开度渐小，阀片向阀座方向回复。由此可见，排气阀片的开启和关闭以及对限位板和阀座的周期性冲击，是系统产生振动和噪声的主要根源之一。

2 排气阀片的振动数学模型及求解

建立排气阀片振动的运动微分方程。由于阀片的厚度远小于其它特征尺寸，根据弹性力学的有关理论，阀片的运动处理为平面薄板的弯曲问题。尽管阀片的位移远大于其厚度，应归属于薄板的大挠度理论范畴，但由于阀片的弹性曲面为可展曲面(无约束)，中面仍接近无应变状态，在分析中仍可应用小挠度理论[5]。

将阀片的运动过程划分为许多微小的时间区段，在任一微小的时间区段Δtj内，阀片的边界条件及气体力可视为常量。阀片卷绕限位板部分的形状符合限位板的型线函数f(x)，未卷绕部分的变形可按等截面悬臂梁来处理。

图3 排气阀片瞬时位移Fig.3 Instantaneous displacement of the discharge valve

在任一微小的时间区段(tjtj+Δtj)，在气流的作用下，阀片离开阀座向限位板运动，此瞬时的位移可按图3进行分解，且近似地表示为

uj(x,t)=f(xj)+f′(xj)(x-xj)+

(1)

uj(x,t)=f(x)x≤xj

(2)

由振动理论知,阀片未卷绕部分按悬臂梁模型处理，略去阻尼因子，它的强迫振动微分方程为

(3)

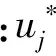
令P(x,t)=0，则得自由振动微分方程

(4)

利用分离变数法,可将解分解为

(5)

将式(5)代入式(4),得

(6)

要使式(6)对任意的x,t都成立,则需两边皆为常数,取该常数值为ω2,则得到两个相应的微分方程

(7)

(8)

式中

(9)

式(7)和式(8)的解分别为

Tj(t)=A1sinωt+A2cosωt

(10)

B3shk(x-xj)+B4chk(x-xj)

(11)

式中:A1、A2为积分常数,由初始条件确定;B1、B2、B3、B4为积分常数,由边界条件确定。

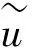
(12)

联立方程(11)与(12)求解，可以得特征方程(频率方程)

cosk(l-xj)chk(l-xj)=-1

(13)

式(13)是一超越方程，用数值解法求得其前4个根是：

k1(l-xj)=1.875,k2(l-xj)=4.694

k3(l-xj)=7.855,k4(l-xj)=10.966

根据式(9)，阀片未卷绕部分的第n阶固有频率为

(14)

第n阶主振型函数为

[shkn(x-xj)-sinkn(x-xj)]

(15)

再求强迫振动微分方程(3)式的解。根据振型叠加法，此解的形式可取

(16)

将式(16)代入式(3)，得

(17)

(18)

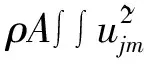
(19)

式(19)的解为

Tjn(t)=Tjn(tj)cosωn(t-tj)+

(20)

p(x,t)外载荷的大小同时受阀片运动位移的影响，随阀隙通流面积的大小而改变。排气阀片振动运动的微分方程和阀片排气口处制冷剂气体流动微分方程是相互耦合的。排气口处气体质量流量的流动方程为(亚临界流动)：

(21)

式中:α为流量系数，Av为阀隙通流面积，(αAv)为有效流通面积，r=pv/p1，pv为通过阀片处压力，p1为工作容积腔压力，K为工质绝热指数，T1为工作容积腔温度，R为气体常数。

将式(15)和式(20)代入式(16)，得到阀片未卷绕部分对任意激励的位移响应，将响应结果代入式(1)，式(1)和式(21)联立求解，从而求得阀片在排气激振过程中各点的瞬时位移。

3 阀片的固有频率和位移计算

本研究的阀片材料为Sandviki 7C27Mo2合金钢，阀片单叶各参数值为：阀片长度l为24 mm，阀片宽度b为9 mm，阀片厚度h为0.305 mm，材料密度ρ为7 872 kg/m3，弹性模量E为206 GPa。根据排气阀片实际工作状态，取某时刻xj为4 mm，求得前5阶模态固有频率ωn为

ω1=623.1 Hz

ω2=3 904.5 Hz

ω3=10 933.9 Hz

ω4=21 309 Hz

ω5=35 416.8 Hz

压缩机正常工况下排气压力为1.35 MPa(表压),压缩机转速为2 400 r/min，限位板型线函数f(x)

根据第1阶主振型，求得阀片在振动过程中最外端的位移(升程)运动轨迹，如图4所示。图中坐标θ为压缩机主轴旋转角度。

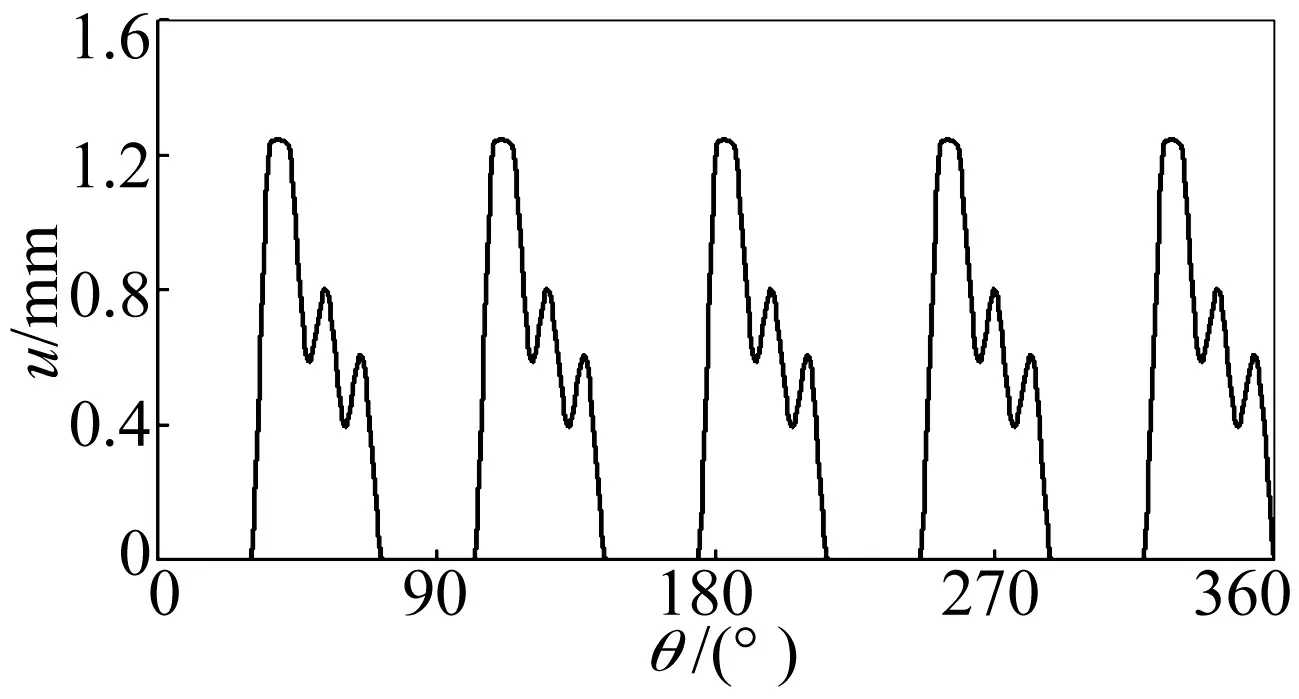
图4 排气阀片最外端位移Fig.4 The displacement of the outermost end of the discharge valve

从图中可见，压缩机主轴旋转一周，排气阀片将承受5次排气冲击，阀片最外端在振动过程中的最大位移为1.23 mm，而此端点对应的限位板高度为1.154 mm，阀片振动的极限位移同限位板高度接近，因此，提高限位板高度或者限制阀片的振幅以控制系统噪声仍然具有一定的空间。

4 排气阀片的UG NX Nastran模态分析

运用有限元分析软件UG NX Nastran，对排气阀片进行模态分析[7]。

NX Nastran模态分析用于分析计算和评估结构的固有频率和自然模态(振型)[8-9]，计算时不考虑阻尼，和外载荷也不相关。材料属性设定为Sandviki 7C27Mo2合金钢，材料泊松比为0.25，选择2D四边形网格，划分单元共421个。根据阀片实际工作状态，对阀片距底边4 mm的区域进行约束。有限元模型如图5所示。

图5 排气阀片网格图Fig.5 Grid diagram of discharge valve

通过计算，得到了阀片的前5阶固有频率和振型。计算结果如表1所示。NX Nastran计算的前5阶固有频率同振动方程求解对应的前5阶固有频率比较接近。其振型如图6所示。图中可见，第1阶振型为阀片从水平面开始向下做单一方向弯曲摆动，阀片最外端振幅最大。根据图2a可知，限位板的设计型线和阀片第1阶振型形状相近，这对于减小撞击速度，降低系统的振动和噪声是有利的。第2阶振型为阀片从单叶水平面开始沿对称中心线扭转摆动，对称中心线是波节线(此线上质点零位移)。第3阶振型为阀片从水平面开始上下弯曲摆动，左端部分向上弯曲，中间部分向下弯曲，两部分交界线是波节线。第4阶振型为阀片从单叶水平面开始沿对称中心线扭转摆动，且左端顺时针方向扭转，中部逆时针方向扭转，对称中心线和左端中部交界线都是波节线。第5阶振型为阀片从水平面开始上下弯曲摆动，左端部分向下弯曲，中间部分向上弯曲，右端部分向下弯曲，三部分形成的两条交界线都是波节线。

表1 计算模态频率

研发的旋叶式压缩机的工作转速设计为800-8 500 r/min，而实用的工作转速为1 000-6 000 r/min。即阀片实际工作频率为83.33-500 Hz，而阀片第1阶固有频率为650.6 Hz，可见其工作频率低于固有频率。因此，排气阀片在工作过程中不会发生共振及由此产生的强烈噪声和排气脉动。

5 压缩机振动和排气脉动及噪声测试

由于排气阀片为压缩机腔内运动部件，阀片的工作状态测试只能在压缩机外部进行。而压缩机的振动，尤其是排气脉动和噪声与阀片的工作状态关系很大。将旋叶压缩机在全消声试验室进行振动、排气脉动及噪声测试，设备安装如图7所示。

振动加速度传感器布置：在外壳的前端安装脚处设置测点1，在外壳(圆柱面)侧面设置测点2，在后端(轴中心)处设置测点3，在三处分别布置加速度传感器，在每测点上安装X轴、Y轴、Z轴三个方向的传感器。

排气脉动传感器安装：在与压缩机排气口相连的150 mm长的硬管的中央安装传感器，测定排气管道内的压力脉动。

图6 有限元模态分析结果Fig.6 Analysis results of finite element modal

图7 旋叶压缩机振动和排气脉动及噪声测试示意图Fig.7 Schematic diagram of rotary vane compressor vibration and exhaust pulsations and noise test

传声器布置：以被测压缩机为圆心，半径为1 m的半球体上阵列了19个传声器。

压缩机在空调系统中按设定工况运行，转速从1 000 r/min升至6 000 r/min，测得压缩机的振动加速度如图8所示。1点处的振动加速度为X向、Y向、Z向加速度的矢量和，2点、3点的加速度亦如此，压缩机的总加速度为三处各方向上的加速度大小平方后再求平方根。图9为测得的速度扫描的排气脉动。图10为测得的速度扫描的声功率。

图中“GMW标准”线为美国通用汽车公司对固定排量的空调压缩机外壳振动加速度、排气脉动和声功率的上限要求。GMW标准是通用汽车公司的全球工程标准，汽车上使用的固定排量空调压缩机的NVH要求按“GMW14789标准”执行，其振动加速度上限的数值等于15.89e(压缩机转速×0.000 51)；排气压力脉动要求是压缩机在5 000 r/min内的任一转速下的排气压力脉动不应超过12 kPa；速度扫描的声功率要求是压缩机噪声在“常规”线以下为合格，在“安静”线以下表明此压缩机已达到安静水平，“常规”值(dB)为0.006×压缩机转速+62，“安静”值(dB)为0.006×压缩机转速+59。测试方法按“GMW14477空调压缩机NVH试验标准”执行。上述振动加速度、排气脉动、声功率的测试方法是按此标准执行的。

由图8可知，压缩机外壳的振动总加速度远低于GMW标准规定上限。图9说明排气压力脉动远小于GMW标准,从图10可见, 速度扫描的声功率低于”常规”标准,接近”安静”标准,因此，压缩机运行是平稳的，排气阀片的运动具有很高的可靠性。

图8 振动测试结果Fig．8Vibrationtestresults图9 排气压力脉动测试结果Fig．9Exhaustpressurepulsationtestresults图10 声功率测试结果Fig．10Soundpowertestresults

6 结 论

通过对排气阀片结构运动分析，建立了阀片振动数学模型，并分析了排气阀片的固有频率及其强迫振动。利用UG NX Nastran模态计算，确定了排气阀片的固有频率和振型，确认排气阀片在工作过程中不会发生共振，压缩机系统也不会由此产生强烈的噪声和排气脉动。测试结果证明，压缩机的外壳振动总加速度、噪声和排气脉动都低于美国通用汽车公司“GMW标准”的规定上限，证明排气阀片工作时的状态是可靠的。但研究结果表明，阀片振动的极限位移同限位板高度比较接近，因此，提高限位板高度或者限制阀片的振幅以进一步控制系统的排气脉动和噪声仍然具有一定的空间。本文的分析结果为排气阀片乃至压缩机整体的故障诊断和振动控制提供了重要参考。

[1] 缪道平，吴业正.制冷压缩机[M].北京：机械工业出版社，2004，219-228.

[2] 阙雄才，陈江平，姚国琦，等.汽车空调实用技术[M].北京：机械工业出版社，2003,134-151.

[3] 马国远，李红旗.旋转压缩机[M].北京：机械工业出版社，2003,121-132.

[4] 卢喜，杨诚.旋叶式汽车空调压缩机的噪声源识别[J].重庆大学学报(自然科学版)，2006，29(8)：70-73. LU Xi,YANG Cheng. Rotary vane automotive air conditioner compressor noise source identification [J]. Journal of Chongqing University (Natural cience),2006,29(8):70-73.

[5] 杨桂通.弹塑性力学引论[M].北京：清华大学出版社，2004,218-235.

[6] 于德介，程军圣，杨宇.机械振动学[M].长沙：湖南大学出版社，2010,77-79.

[7] 傅志方.振动模态分析与参数识别[M].北京:机械工业出版社,1990,85-96.

[8] 沈春根，王贵成，王树林，等.UG NX 7.0有限元分析入门与实例精讲[M].北京：机械工业出版社，2010,181-217.

[9] 朱崇高，谢福俊.UG NX CAE基础与实例应用[M].北京：清华大学出版社，2010,162-167.

Vibration behavior of a discharge valve for vane comparessor of a car air conditioner

LI Chun-yin1，WANG Shu-lin2

(1.College of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093，China；2.College of Material Science and Engineering, University of Shanghai for Science and Technology, Shanghai 200093，China)

Discharge valve is one of the key parts for vane compressor of a car air conditioner, and it is also one of the main vibration noise sources of the compressor. Through the dynamic analysis of the discharge valve structure, a mathematical model for the value vibration was constructed, and its natural frequencies and forced vibration were solved. With UG NX Nastran, the modal frequencies and modal shapes of the discharge valve were obtained. The test results showed that the compressor shell vibration acceleration, noise and exhaust pulsation are lower than their upper limits in the GMW standards of the General Motors Corp., USA, so the working condition of the discharge valve is reliable. However, the study results showed that the ultimate displacement of the valve vibration is relatively close to the height of restrictor plates; therefore, there still remains some space for raising the height of restrictor plates or limiting the vibration amplitude of the valve for further control of the exhaust pulsation and noise of the system. This study provided a reference for vibration control and fault diagnosis of a discharge valve even the overall vane compressor.

vane compressor；air conditioner compressor；discharge valve；vibration and noise control; modal analysis

2013-01-10 修改稿收到日期：2013-05-03

李春银 男，硕士，高工，1965年9月生

王树林 男，教授，博士生导师，1951年生

TB533+.1

A

10.13465/j.cnki.jvs.2014.08.032