约束阻尼结构的双向渐进拓扑优化

房占鹏， 郑 玲

(重庆大学 机械传动国家重点实验室，重庆 400044)

约束阻尼结构的双向渐进拓扑优化

房占鹏， 郑 玲

(重庆大学 机械传动国家重点实验室，重庆 400044)

针对约束层阻尼板的拓扑优化问题，以模态损耗因子最大化为目标函数，约束阻尼材料体积分数为约束条件，建立了约束阻尼板的拓扑优化模型。基于模态应变能方法，推导了目标函数对设计变量的灵敏度。采用双向渐进优化算法(BESO)对约束阻尼材料的布局进行了拓扑优化，获得了约束阻尼材料的最优拓扑构型，并与渐进优化算法(ESO)进行了比较。研究结果表明：双向渐进优化算法相比渐进优化算法，获得的模态损耗因子更高，阻尼减振效果更好。

约束阻尼;模态损耗因子;拓扑优化;双向渐进优化法

阻尼结构能有效抑制结构的振动与噪声，特别是约束阻尼结构对宽带随机振动响应有很好的抑制作用，广泛应用于汽车、航空航天、舰船等行业。在传统的阻尼结构减振设计中，将阻尼材料覆盖于整个结构的表面，有效抑制结构振动和噪声的同时，也增加了结构的附加质量。

对约束阻尼材料的布局进行优化配置能够有效提高约束阻尼材料的使用效率，减少约束阻尼材料的使用量。Zheng等[1]以振动能量最小化为目标，采用遗传算法对约束阻尼梁进行了优化分析。杨德庆等[2-3]提出了阻尼胞单元和阻尼拓扑敏度等概念，利用均匀法方法对自由阻尼层结构进行了阻尼材料优化配置，指出阻尼优化配置是减振降噪设计的有效途径。Zheng等[4]针对圆柱壳体结构用解析方法研究了分片阻尼的结构特性，探讨了分片布置约束阻尼的布局优化问题。Chia等[5]结合有限元分析，采用胞元自动控制算法(cellular automata) 对约束阻尼板结构的布局进行优化，并采用理论计算和实验验证了优化算法的有效性。Zheng等[6]以模态阻尼比最大化为目标，采用移动渐近线算法(MMA)对约束阻尼板进行优化，得到了优化构型，并指出移动渐近线算法对约束阻尼圆柱壳的优化也有很好的求解效果。

1993年，Xie等[7]提出了渐进优化算法，它通过将无效或低效的材料逐步去掉，使得结构逐渐趋于优化，该算法通用性好，计算效率高，已经在应力、位移、刚度，振动频率、相位、临界压力等优化问题中得到广泛的应用。郭中泽等[8]将渐进优化算法应用到了自由阻尼材料最优配置问题。李超等[9]采用渐进优化算法对约束阻尼圆柱壳的约束阻尼材料进行优化配置。在采用渐进优化算法对结构进行拓扑优化的过程中，某些被删除的低效率的单元可能变为高效率的单元，但是渐进优化算法不能将这些删除单元恢复为实体单元，影响了优化算法的可靠性，使优化结果出现低效局部优化解。双向渐进优化算法[10]是对渐进优化算法的改进，它不仅可以删除材料，还可以添加材料，使得材料布局更加合理，因此，该方法具有更好的优化设计能力。

本文采用双向渐进优化算法，以模态损耗因子为目标函数，约束阻尼材料用量为约束条件，建立了约束阻尼结构的拓扑优化模型。基于模态应变能的方法推导了约束阻尼单元的灵敏度。编制双向渐进优化算法的优化流程，对模态损耗因子最大化的约束阻尼材料最优分布问题进行研究。

1 约束阻尼板的动力学模型

1.1 有限元模型

约束层阻尼板的单元结构如图1所示，建模时作如下假设：

(1) 忽略约束层和基层的剪切变形；

(2) 不计转动惯量；

(3) 同一截面任一点的横向位移和转角相同；

(4) 各层材料之间粘贴牢固，层间无相对滑动。

图1 约束层阻尼板单元示意图Fig.1 A schematic drawing of an element in FE structure of plate with CLD treatments

1.2 变形关系

结构的应变关系表达式如下：

(1)

1.3 单元的自由度与形函数

构造约束阻尼板单元包含4个物理节点，每一个物理节点有7个自由度，分别是基层面内的两个位移分量up和vp；约束阻尼层面内的两个位移分量uc和vc；约束阻尼板的横向位移w；中性面的两个旋转角θx和θy。下标p，v，c分别表示基本、粘弹性阻尼层和约束层。它们的插值函数如下式：

uc=a1+a2x+a3y+a4xy

vc=a5+a6x+a7y+a8xy

up=a9+a10x+a11y+a12xy

vp=a13+a14x+a15y+a16xy

w=a17+a18x+a19y+a20x2+a21xy+a22y2+

a23x3+a24x2y+a25xy2+a26y3+a27x3y+a28xy3

(2)

式中：{a}={a1a2…a28}可由每个单元位移矢量{Δe}确定，单元的位移矢量可表示为

{Δe}={Δ1Δ2Δ3Δ4}T

式中：{Δi}={ucivciupivpiwiθxiθyi}T(i=1,2,…,4)

因此，单元内的任意点位移{Δ}={ucvcupvpwθxθy}T可由单元的四个节点位移矢量插值得到：

{ucvcupvpwθxθy}T=

{[N1][N2][N3][N4][N5][N5],y[N5],x}{Δ(e)}

式中：[N1],[N2],[N3],[N4],[N5],[N5],y和 [N5],x分别为位移矢量uc,vc,up,vp,w,θx和θy所对应的形函数。

1.4 单元的运动方程

约束阻尼板单元的动能和应变能表达如下：

约束阻尼板单元的动能：

(1) 基板单元：

(3)

(2) 约束层单元：

(4)

(3) 阻尼层单元：

(5)

约束阻尼板单元的应变能：

(1) 基板单元：

(6)

(2) 约束层单元：

(3) 阻尼层单元：

(8)

(9)

将单元应变能及单元动能代入Hamilton原理变分公式，可得第e个单元的运动方程：

(10)

式中：F(e)为外界对单元的激励作用力，M(e)为单元的质量矩阵：

(11)

K(e)为单元的刚度矩阵:

(12)

将单元的质量矩阵和刚度矩阵组装为约束阻尼板的总质量矩阵和总刚度矩阵：

(13)

(14)

因此，约束阻尼板的有限元动力学方程为

(15)

2 拓扑优化模型

约束阻尼结构主要通过粘弹性层的剪切变形把振动能量转化为热能，实现振动能量的耗散，达到抑制振动的目的。约束阻尼结构对能量的耗散与模态损耗因子直接相关。因此，约束阻尼结构的拓扑优化以模态损耗因子最大化为目标函数，以达到对模态振动的有效控制。以模态损耗因子最大化为目标函数，约束阻尼材料使用量为约束条件，建立的拓扑优化模型为

(16)

式中：设计变量xi是约束阻尼材料的第i个单元(包括阻尼单元和阻尼单元所对应的约束单元)的存在状态，取值为1和xmin。1代表结构表面覆盖阻尼材料和约束材料。xmin代表删除了结构表面覆盖的阻尼材料和约束材料，为了防止刚度矩阵出现奇异，本文取值为0.001；n为约束阻尼材料单元的总数；ηr是第r阶模态损耗因子。V为约束阻尼材料的体积；V*是体积约束。

3 灵敏度分析和数值不稳定的抑制

3.1 灵敏度分析

根据Johnson等[11]提出的附加阻尼结构的模态应变能(MSE)的方法，可以得到第r阶模态损耗因子为

(17)

其中，ηv为阻尼材料的损耗因子；Uvr和Ur分别为第r阶模态的阻尼材料应变能和约束阻尼结构总应变能；Φr是第r阶结构弹性分析得到的实模态振型。

令ηr对设计变量xi求偏导，第r阶模态损耗因子关于设计变量的灵敏度可以计算如下：

(18)

阻尼材料的刚度矩阵和约束阻尼结构的刚度矩阵分别为

(19)

令式(19)对设计变量xi求偏导，得：

(20)

将式(20)代入式(19)：

(21)

则约束阻尼单元i的灵敏度βi为

βi=

(22)

如果要使前m阶的模态损耗因子最大化，可以按照这些模态在响应中的比重相加，得到一个模态损耗因子的函数：

(23)

模态损耗因子的函数关于设计变量xi的灵敏度表示如下：

(24)

通过式(24)就可以得到前m阶模态损耗因子最大化的模态损耗因子关于设计变量xi的灵敏度。

3.2 数值不稳定的抑制

在拓扑优化过程中常见的数值不稳定现象主要有灰度单元、局部极值、棋盘格式、网格依赖性现象。采用双向渐进优化算法进行拓扑优化，数值不稳定性主要表现为棋盘格式和网格依赖性。Sigmund等[12]提出的不依赖于网格尺寸的网格独立滤波法，它实现起来简单，并且对优化目标函数没有影响。网格独立滤波法是以滤波半径范围内单元的灵敏度的加权平均值修正原单元的灵敏度值，从而获得滤波后单元灵敏度信息的重新分布。网格独立滤波的表达式为

(25)

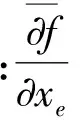
Hi=rmin-dist(e,i),

(26)

rmin为滤波器半径；dist(e,i)为单元e和单元i的中心距离。

采用网格独立滤波技术，最重要的是选择合适的滤波半径，对约束阻尼单元的灵敏度信息进行重新分布，抑制棋盘格式和网格依赖性等数值不稳定问题。

4 约束阻尼结构拓扑优化的实现流程

渐进优化算法把判定为低效的单元删除，使该单元设计变量为0，在以后的迭代过程中不参与灵敏度的计算。双向渐进算法是对渐进优化算法的改进，它将判定为低效单元的设计变量设定为一个极小值，并在以后迭代的过程中通过滤波得到其灵敏度。当被删单元被判定为高效单元时，将其设计变量由极小值转变为1，使其恢复为实体单元。图2为拓扑优化流程图，具体的步骤如下：

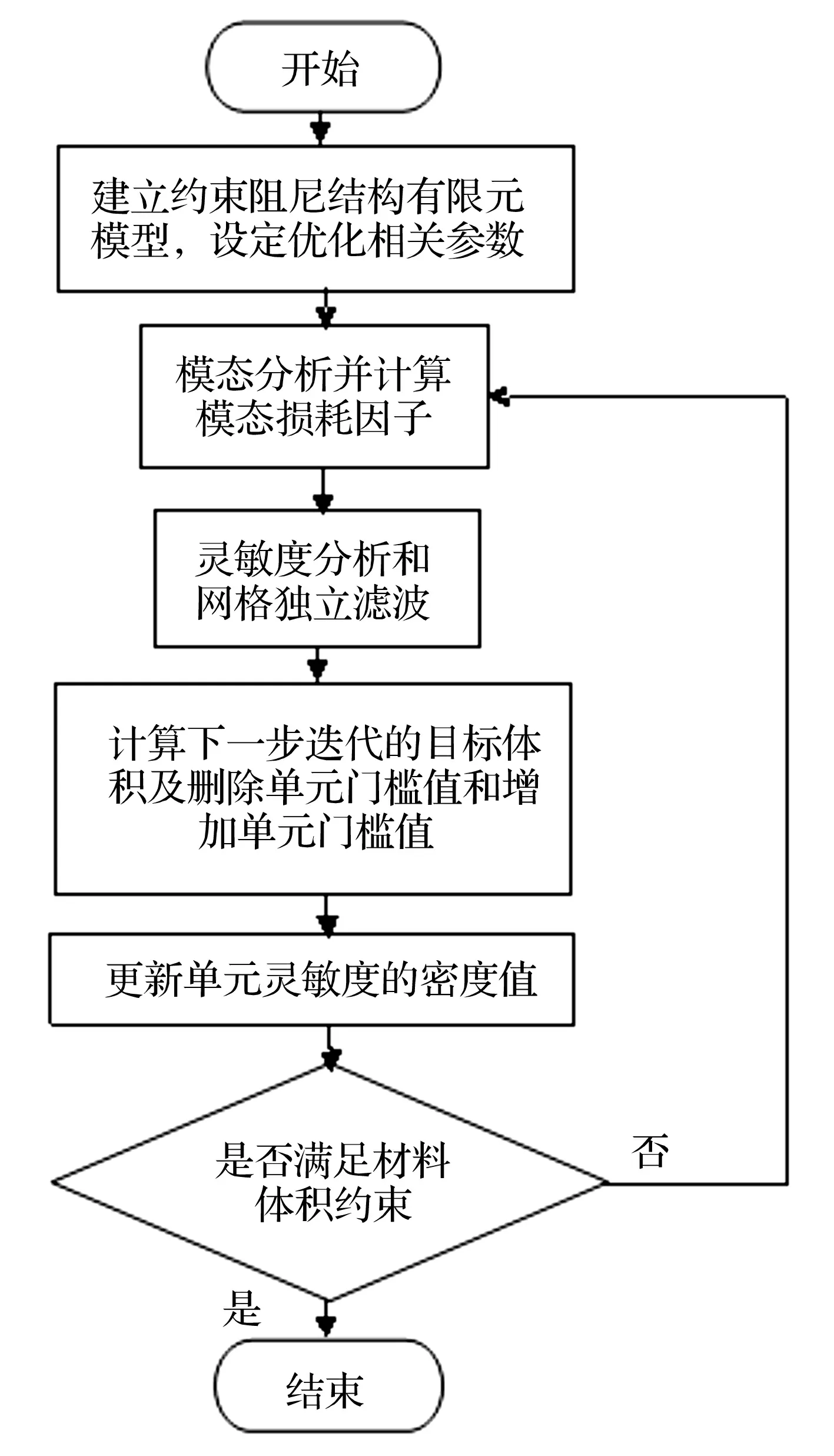
图2 拓扑优化流程图Fig.2.Diagram for the topology optimization procedures

(1) 将约束阻尼材料覆盖于结构的表面，构建全覆盖的约束阻尼结构，并建立其有限元模型。此时，设计变量xi的值均为1；

(2) 设定约束阻尼材料的体积约束量V*和进化率ER等双向渐进优化算法的相关参数；

(3) 对建立的约束阻尼有限元模型进行模态分析，并采用模态应变能的方法计算约束阻尼结构的模态损耗因子；

(4) 根据式(22)或式(24)式计算约束阻尼材料每个实体单元的灵敏度，并采用网格独立滤波技术对单元的灵敏度进行滤波并得到删除单元的灵敏度。

(5) 计算下一步迭代的约束阻尼材料的目标体积，当下一步迭代的约束阻尼材料的体积Vk+1小于设定的约束阻尼材料的体积约束V*，计算公式为

Vk+1=Vk(1-ER)

(27)

当Vk+1大于等于V*时，使Vk+1=V*。根据Vk+1决定删除单元门槛值βdel和增加单元门槛值βadd；

(6) 更新单元的密度值。当单元的灵敏度βi≤βdel，实体单元设计变量xi的密度值由1变为xmin，当单元的灵敏度βi>βdel，删除单元设计变量xi的密度值由xmin变为1。

(7) 重复步骤(3)-(6)，直至满足约束阻尼材料体积约束条件，结束迭代，输出各相关数据。

5 算 例

约束阻尼悬臂板的基板为铝板，板长0.2 m，宽0.1 m，厚度为2 mm，密度为2 800 kg/m3，弹性模量为70e9 Pa，泊松比为0.3。在铝板表面覆盖约束阻尼材料，阻尼材料厚度为0.3 mm，密度为1 200 kg/m3，弹性模量为12e6 Pa，泊松比为0.495，损耗因子为0.5。约束材料厚度为0.5 mm，密度为2 700 kg/m3，弹性模量为70e9 Pa，泊松比为0.3。约束阻尼板左端全约束。

本文在MATLAB中编制了约束阻尼板的有限元模型及拓扑优化程序。以全覆盖的约束阻尼材料使用量的50%为约束条件，分别以一阶、二阶、三阶和四阶模态损耗因子最大化为优化目标，采用文献[8]的渐进优化算法和双向渐进优化算法对约束阻尼结构进行拓扑优化。

图3 一阶模态损耗因子最大化的拓扑构型Fig.3 Optimal distribution of damping material for maximization of the first modal loss factor

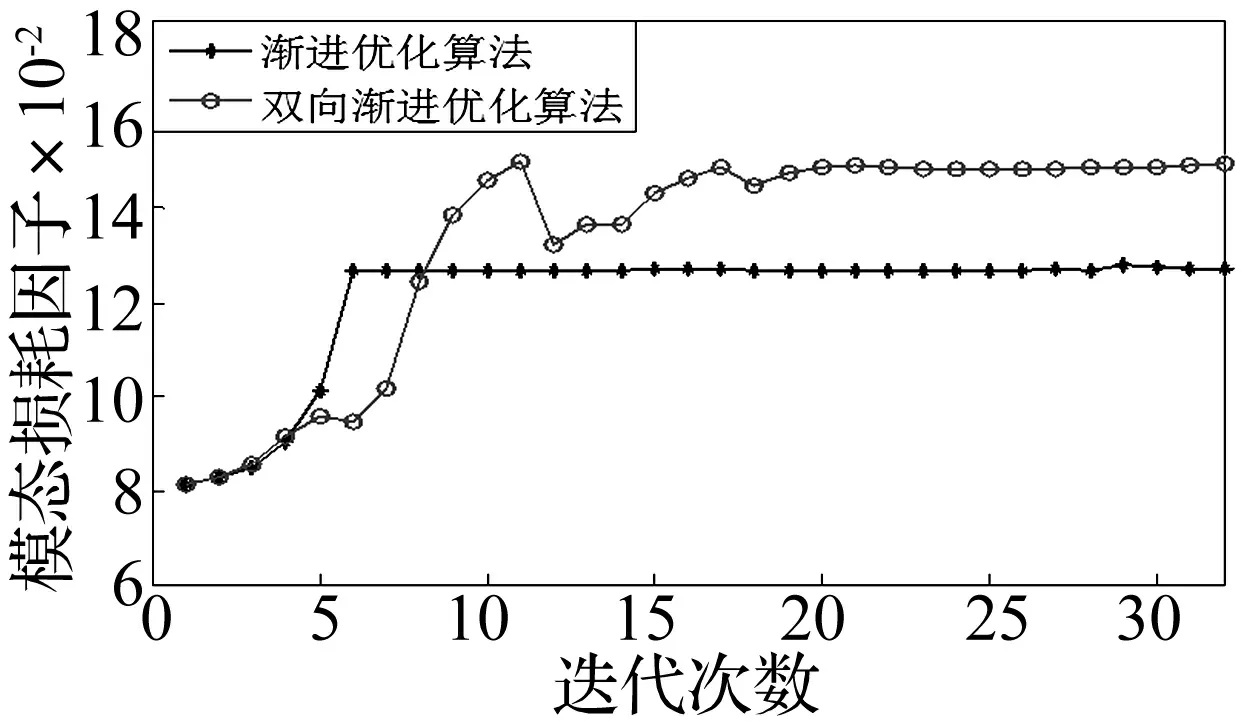
图4 一阶模态损耗因子的迭代过程Fig.4 Iteration histories for the first modal loss factor

从图4可以看出，随着迭代次数的增加，附加约束阻尼材料逐渐减小，一阶的模态损耗因子不仅没有减小，反而有较大幅度的增加。第八次迭代以后，采用双向渐进优化算法的损耗因子的变化曲线要明显高于采用渐进优化算法的变化曲线，其拓扑优化构型的模态损耗因子更大。拓扑构型如图3所示，黑色为粘贴约束阻尼材料的位置。

图5 二阶模态损耗因子最大化的拓扑构型Fig.5.Optimal distribution of damping material for maximization of the second modal loss factor

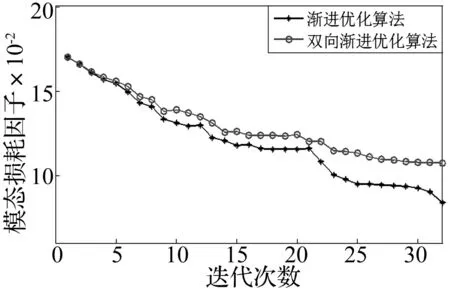
图6 二阶模态损耗因子的迭代过程 Fig.6 Iteration histories for the second modal loss factor

图7 三阶模态损耗因子最大化的拓扑构型Fig.7 Optimal distribution of damping material for maximization of the third modal loss factor

图8 三阶模态损耗因子的迭代过程Fig.8. Iteration histories for the third modal loss factor

图9 四阶模态损耗因子最大化的拓扑构型Fig.9 Optimal distribution of damping material for maximization of the fourth modal loss factor

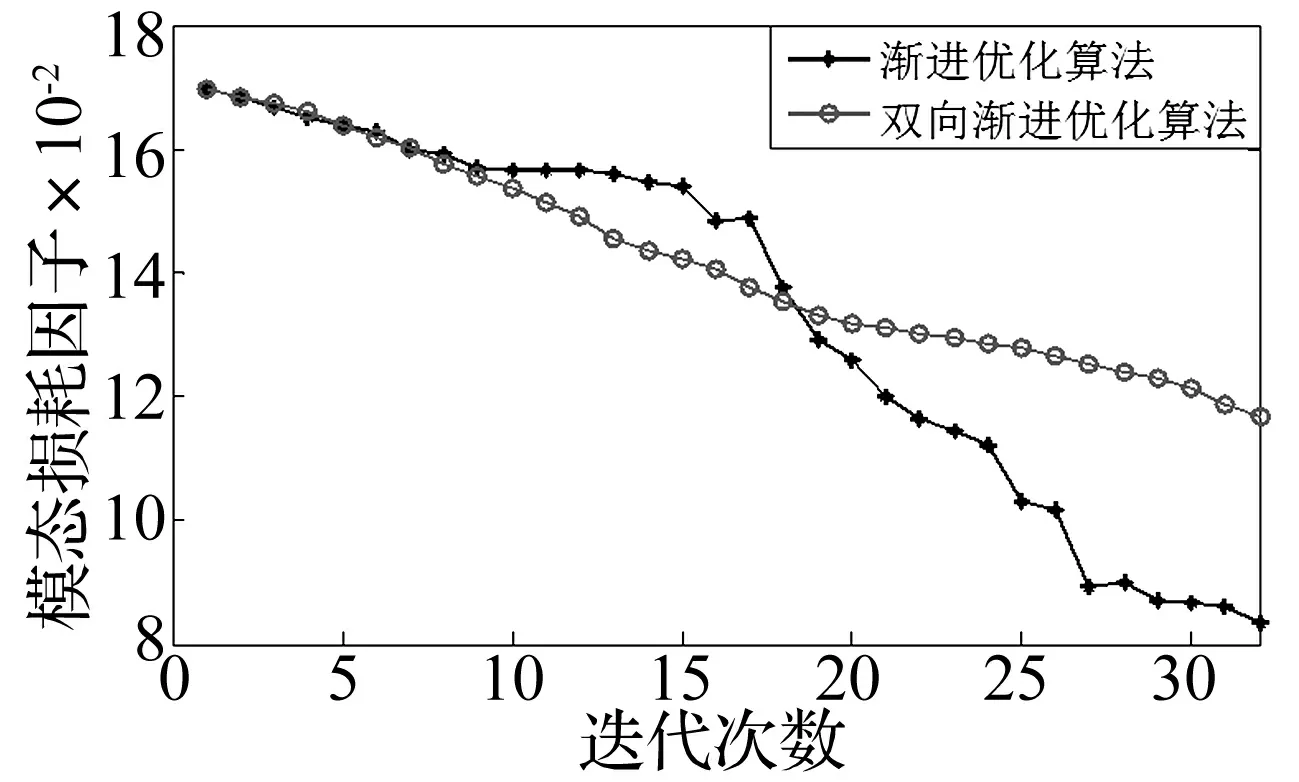
图10 四阶模态损耗因子的迭代过程Fig.10. Iteration histories for the fourth modal loss factor

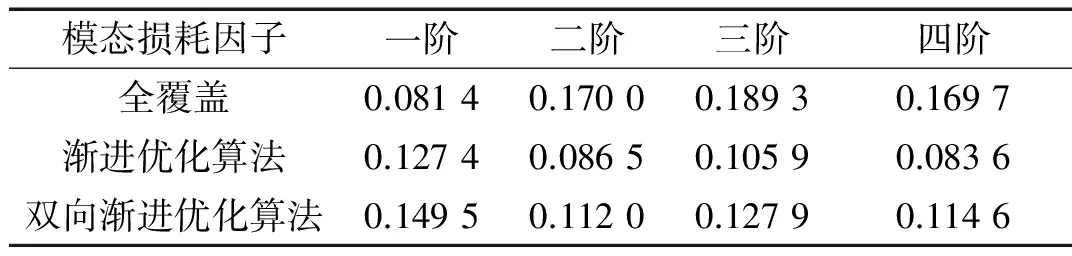
模态损耗因子一阶二阶三阶四阶全覆盖0．08140．17000．18930．1697渐进优化算法0．12740．08650．10590．0836双向渐进优化算法0．14950．11200．12790．1146

图6、图8和图10分别为二阶、三阶和四阶的模态损耗因子的迭代过程图。从图中可以看出，随着迭代次数的增加，约束阻尼材料逐渐减少，模态损耗因子也缓慢下降。双向渐进优化算法的迭代曲线基本都要高于渐进优化算法的迭代曲线。两种优化算法以二阶、三阶和四阶模态损耗因子最大化的拓扑构型如图5、图7和图9所示，黑色为粘贴约束阻尼材料的位置。

从表1中可以看出：在约束阻尼材料使用量只有全覆盖的50%的情况下，采用双向渐进优化算法得到的拓扑构型的模态损耗因子明显大于采用渐进优化算法得到的拓扑构型的模态损耗因子。优化结构的模态损耗因子与全覆盖结构的模态损耗因子对比：采用渐进优化算法和双向渐进优化算法的一阶模态损耗因子比全覆盖的分别增加了56.5%和83.7%；采用渐进优化算法二阶、三阶和四阶的模态损耗因子比全覆盖的分别减小了49.1%、44.1%和50.7%；采用双向渐进优化算法二阶、三阶和四阶的模态损耗因子比全覆盖的分别减小了34.1%、32.4%和32.5%。

6 结 论

本文基于双向渐进优化算法对约束阻尼结构中的约束阻尼材料布局进行了优化设计。建立了约束阻尼结构的拓扑优化模型，基于模态应变能的方法推导了目标函数关于约束阻尼单元的灵敏度。对比了渐进优化算法和双向渐进优化算法对约束阻尼悬臂板的拓扑优化结果：采用双向渐进优化算法得到的拓扑构型的模态损耗因子均高于采用渐进优化算法得到的拓扑构型的模态损耗因子。表明了双向渐进优化算法不仅能够删除低效率的单元，而且可以将删除的高效单元恢复为实体单元，具有更好的优化能力，对约束阻尼结构进行拓扑优化，得到的拓扑构型比渐进优化算法更优。

[ 1 ] Zheng H，Cai C，Tan X M. Optimization of partial constrained layer damping treatment for vibrational energy minimization of vibrating beams [J]. Computers and Structures, 2004, 82(29-30): 2493-2507.

[ 2 ] 杨德庆,柳拥军,金咸定.薄板减振降噪的拓扑优化设计方法[J]. 船泊力学, 2003, 7(5): 91-96. YANG De-qing, LIU Yong-jun, JIN Xian-ding. Structural topology optimal design to reduce vibration and noise of thin plate [J]. Journal of Ship Mechanics, 2003, 7(5): 91-96.

[ 3 ] 杨德庆.动响应约束下阻尼材料配置优化的拓扑敏度法[J]. 上海交通大学学报, 2003, 37(8): 1109-1212, 1125. YANG De-qing. Topological sensitivity method for the optimal placement of unconstrained damping materials under dynamic response constraints [J]. Journal of Shanghai Jiaotong University, 2003, 37(8):1109-1212, 1125.

[ 4 ] Zheng H, Cai C, Pau G S H, et al. Minimizing vibration response of cylindrical shells through layout optimization of passive constrained layer damping treatments [J]. Journal of Sound and Vibration, 2005, 279(3-5):739-756.

[ 5 ] Chia C M，Rongong J A，Worden K. Strategies for using cellular automata to locate constrained layer damping on vibrating structures [J]. Journal of Sound and Vibration, 2009, 319(1-2): 119-139.

[ 6 ] ZHENG Ling, XIE Rong-lu, WANG Yi,et al. Topology optimization of constrained layer damping on plates using Method of Moving Asymptote (MMA) approach [J]. Shock and Vibration, 2011, 18(1-2): 221-244.

[ 7 ] Xie Y M, Steven G P. A simple evolutionary procedure for structural optimization[J]. Computers and Structures, 1993, 49(5): 885-896.

[ 8 ] 郭中泽,陈裕泽,侯强，等. 阻尼材料布局优化研究[J]. 兵工学报,2007, 28(5): 638-640. GUO Zhong-ze, CHEN Yu-ze, HOU Qiang, et al. Damping material optimal placement in damping structure design [J]. Acta Armamentarii, 2007, 28(5):638-640.

[ 9 ] 李超,李以农,施磊,等.圆柱壳体阻尼材料布局拓扑优化研究[J]. 振动与冲击,2012, 31(4): 48-52. LI Chao，LI Yi-nong，SHI Lei, et al. Topological optimization for placement of damping material on cylindrical shells [J]. Journal of Vibration and Shock, 2012, 31(4): 48-52.

[10] Huang X, Zuo Z H, Xie Y M. Evolutionary topological optimization of vibrating continuum structures for natural frequencies [J]. Computers and Structures, 2010，88: 357-364.

[11] Johnson C D，Kienholz D A . Finite element prediction of damping in structure with constrained viscoelastic layers [J]. AIAA Journal, 1982, 20(9): 1284-1290.

[12] Sigmund O，Petersson J. Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima [J]. Structural Optimization, 1998, 16: 68-75.

Topological optimization for constrained layer damping material in structures using BESO method

FANG Zhan-Peng, ZHENG Ling

(State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)

A topological optimization model was established to obtain an optimized layout of constrained layer damping material on a plate with passive constrained layer damping (PCLD) treatment. The maximization of modal loss factor was taken as an objective function to enhance damping of this plate. The volume fraction of constrained layer damping material was selected as the constrained condition of the model. The sensitivity of the objective function to design variables was deduced by using the modal strain energy method. The bi-directional evolutionary structural optimization (BESO) method was proposed to search the optimal layout of constrained layer damping material. The numerical examples were illustrated to demonstrate the effectiveness of the proposed BESO method. The results were compared with those with the conventional evolutionary structural optimization (ESO) method. It was demonstrated using that the proposed BESO method can be used to achieve higher modal loss factor for the plate with PCLD treatment than using conventional ESO method does; the damping effect of the plate is enhanced and the effectiveness of the proposed BESO method is verified.

constrained damping; modal loss factor; topological optimization; bi-directional evolutionary structural optimization (BESO)

机械传动国家重点实验室科研业务费(0301002109165)

2013-01-04 修改稿收到日期：2013-05-03

房占鹏 男，博士生，1985年生

郑玲 女，教授，博士生导师，1963年生

TB53

A

10.13465/j.cnki.jvs.2014.08.029