三层结构模型的内共振和组合共振
2014-08-11吴志强陈世栋宫明旭
吴志强, 陈世栋,2, 雷 娜,2, 宫明旭
(1.天津大学 机械工程学院力学系,天津 300072;2.北汽福田汽车股份有限公司 工程研究总院,北京 102206)
三层结构模型的内共振和组合共振
吴志强1, 陈世栋1,2, 雷 娜1,2, 宫明旭1
(1.天津大学 机械工程学院力学系,天津 300072;2.北汽福田汽车股份有限公司 工程研究总院,北京 102206)
主要对三层结构模型的内共振和组合共振实验进行了研究。通过模态设计使得结构一、二阶模态频率之比接近1:3。经振动台水平基础激励实验发现:以一阶模态频率、二阶模态频率激励,都可激发出一、二阶模态间的内共振行为,同时该结构中还存在多种组合共振行为。为下一步非线性振动实验装置的改进奠定了基础。
三层结构;内共振;组合共振
组合共振、内共振现象均是非线性系统典型行为。尽管已有大量的理论分析[1-3]工作,但实验研究的报道并不多。
文献[4-5]分别针对T型梁、悬臂梁开展了实验研究,发现了结构存在内共振,并且能量是从低振幅高频率向高振幅低频率传递。由于内共振提供了传递能量的手段,将激励的能量通过直接激发的模态传递到非直接激发的基本模态中。文献[6]对旋转结构的内共振和组合共振进行了实验研究。实验表明由于内共振的存在,将会诱发结构产生混沌运动。文献[7]从理论分析和实验研究两方面对双铰圆拱进行非线性分析,结果表明其存在跳跃现象以及内共振现象。文献[8]对参激屈曲梁的倍周期分岔和混沌运动进行了实验研究,在实验中观察到了周期吸引子和混沌吸引子共存以及间隙混沌现象。文献[9]通过对文物“龙洗”进行了非线性振动实验,发现水珠喷起现象就是干摩擦引起的自激振动与壳液耦合系统具有两个镜面对称结构的湿模态巧妙结合相互作用的结果。从而解释了中华文物龙洗有趣现象的产生所具有的深刻科学道理。文献[10]对内共振和外共振联合作用下的索-梁组合结构非线性振动问题进行了研究,研究发现索和梁之间在特定的内外共振下才会出现持续的模态交替现象。
随着人们对非线性动力学认识的加深,以工程装备、工程结构为背景的非线性实验研究的重要性越来越得到重视[11]。
在结构工程领域,多层结构的是经常使用的形式之一,如海上采油平台等等,如何避免非线性现象造成此类的结构破坏是值得探讨的问题。作为非线性动力学实验探索,本文选择三层结构模型(见图1)为对象进行内共振及组合共振实验分析。
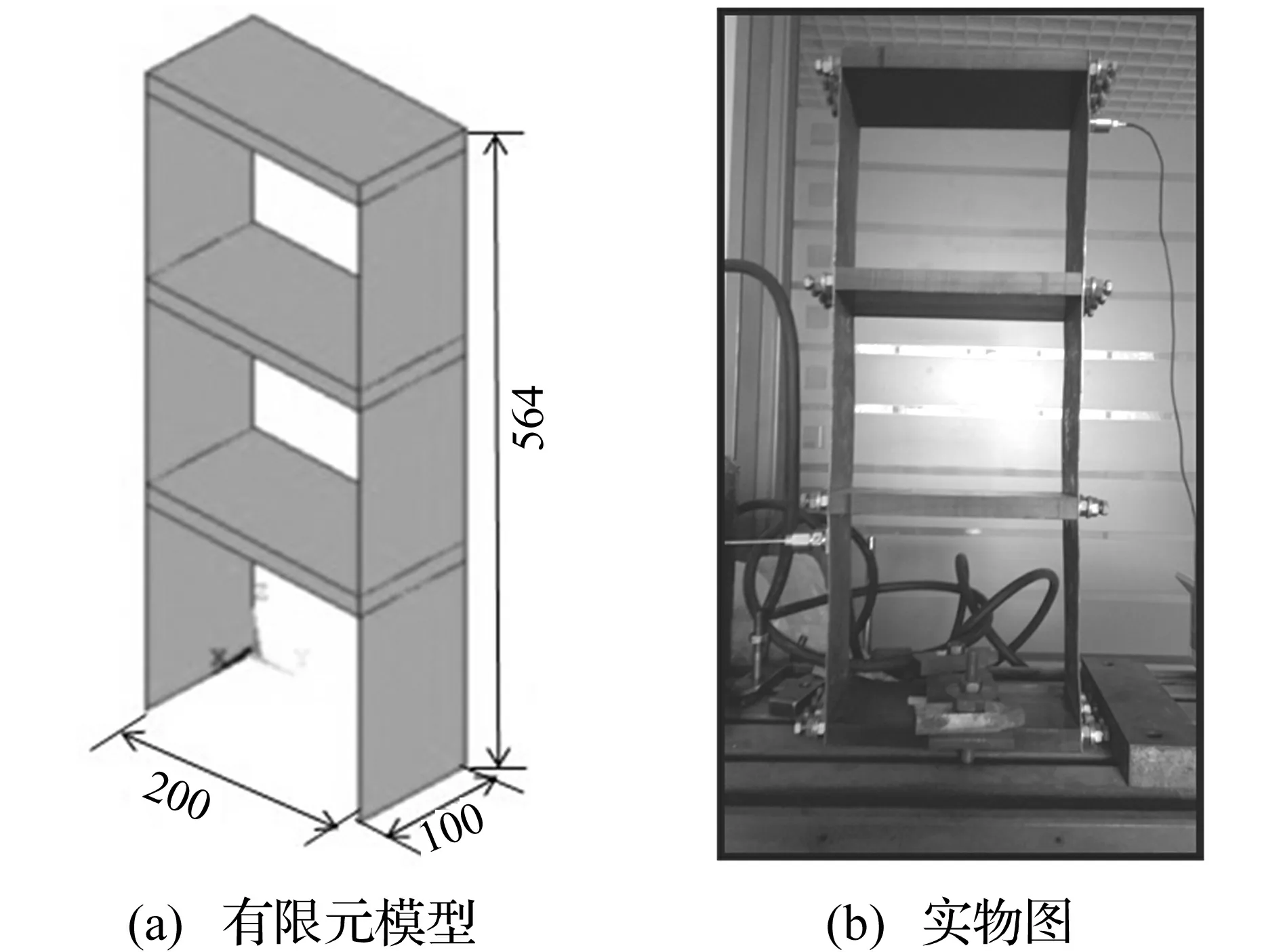
图1 三层结构Fig.1 Three-story structure
1 实验装置及模态参数
本文讨论的结构模型如图1所示。选择这种结构形式,主要的原因是尺寸参数易于调节且便于加工制造,较易通过模态设计实现模态频率间的内共振关系。采用市场常见的材料,经有限元试算,确定出合理的结构参数进行加工。
该结构主要由竖直承重板和结构横梁组成。
竖直承重板:共两块,采用Q235的冷轧钢板,其材料密度为7 800 kg/m3,弹性模量为2.2×1011Pa,泊松比为0.3。钢板厚度为1 mm,用线切割工艺将钢板加工成564 mm×100 mm的长方形板材,在板的长度方向打四排固定孔,孔径为8 mm,孔距为25 mm,为钢板与结构横梁连接螺栓安装预留。
结构横梁:共四块200 mm×100 mm,采用高密度聚乙烯材质,其材料密度为1 500 kg/m3,弹性模量为1.2×109Pa,泊松比为0.4。经表面铣平后,在两端截面处对照竖直承重板的螺栓安装预留孔位置螺纹,螺纹直径8 mm。
组装:用螺栓、垫片、螺母将四块聚乙烯横梁和两块钢板装配在一起,结构的层高为188 mm。注意调整装配间距,减小装配应力,保证装配结构水平竖直。
实验用到的仪器及软件主要包括:TST5912动态信号测试分析系统、TSTMP模态分析软件、力锤、功率放大器、传感器以及激振台等。
为确定模型结构的力学参数,先开展模态实验。首先在模态分析软件中进行参数设置,建立三层结构模型;其次在模型中左右各设置三个测点(测点位于每排螺钉中点位置),在三层结构对应的位置布置相应的测点,并利用锤击法依次对每个测点进行敲击,利用传感器采集数据;最后利用软件进行计算分析,得到结构的幅频响应图如图2所示。由此可读取结构的前三阶固有频率,其与有限元结果基本一致(见表1)。
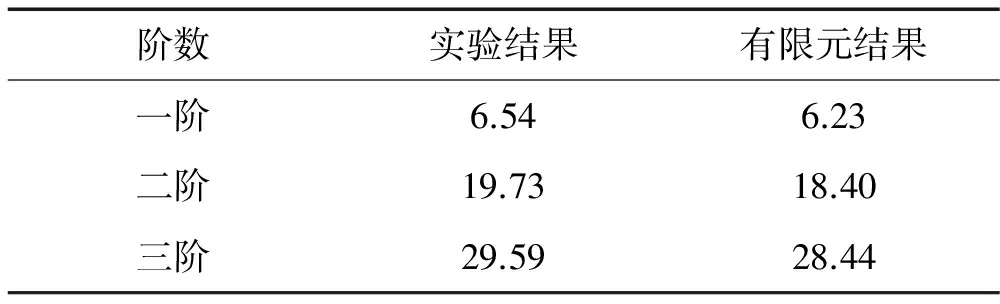
表1 结构前三阶模态频率
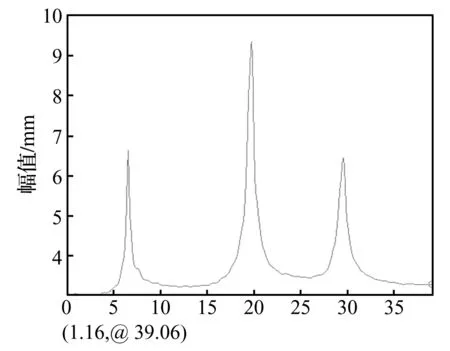
图2 幅频响应Fig.2 Amplitude-frequency response
实验和理论计算都表明:第一阶频率和第二阶频率之比接近1∶3。单纯频率关系还不能保证内共振现象的发生。为弄清该结构中否存在1∶3内共振现象,以下利用电磁振动台开展了水平基础激励下的结构动力学实验研究。

图3 激振台实验装置Fig.3 Device of actuating vibration table
2 内共振现象
利用振动台对结构进行激振,当外激励频率为第一阶模态的固有频率6.54 Hz时,可以将第二阶的模态频率19.73 Hz激发出来,其功率谱图见图4。
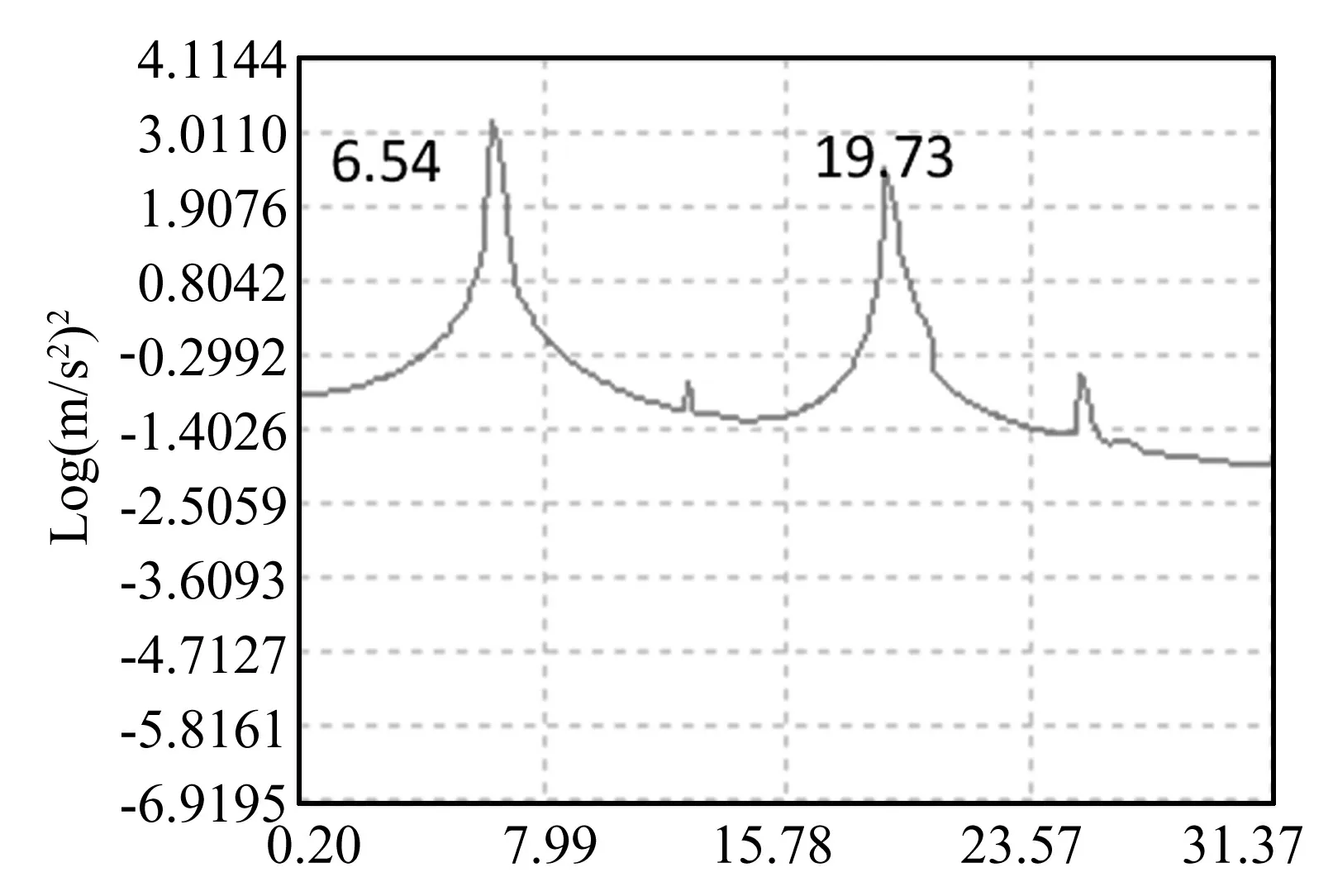
图4 激振频率为6.54 Hz时的功率谱Fig.4 Power spectrum when exciting frequency is 6.54 Hz
当外激励频率为第二阶模态的固有频率19.73 Hz时,也可以将第一阶的模态频率6.54 Hz激发出来,如图5所示。
以上实验表明,激励的能量可以通过直接激发的模态传递到非直接激发的模态中,即可由低阶模态向高阶模态传递能量,也可由高阶模态向低阶模态传递能量。这说明结构中确实存在1∶3内共振现象。
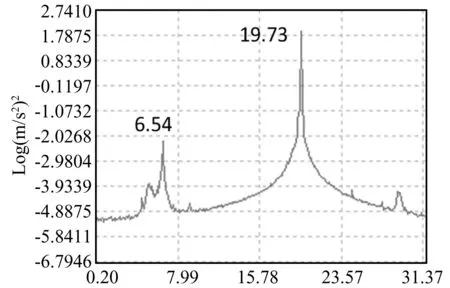
图5 激振频率为19.73 Hz时的功率谱Fig.5 Power spectrum when exciting frequency is 19.73 Hz
3 组合共振实验现象
在较低频率激励下,发现结构中存在多种组合共振现象。
① 当组合激励频率Ω=4.93 Hz时,其组合形式为:(29.59-19.73)/2。对应自功率谱如图6所示。

图6 在4.93Hz处的功率谱Fig.6 Power spectrum when exciting frequency is 4.93 Hz
在图6中,当激振频率为4.93 Hz时,可以将结构的第二阶和第三阶频率激发出来,这两个频率恰好是组合频率构成的元素。在图中也存在其他频率成分,这些是倍周期频率成分。
② 当组合激励频率Ω=9.86 Hz时,其组合形式为:(29.59-19.73)。对应自功率谱如图7所示。
在图7中,当激振频率为9.86 Hz时,可以将结构的第二阶和第三阶频率激发出来,这两个频率恰好是组合频率构成的元素。
③ 当组合激励频率Ω=13.19 Hz时,其组合形式为:(19.73-6.54)。对应自功率谱如图8所示。
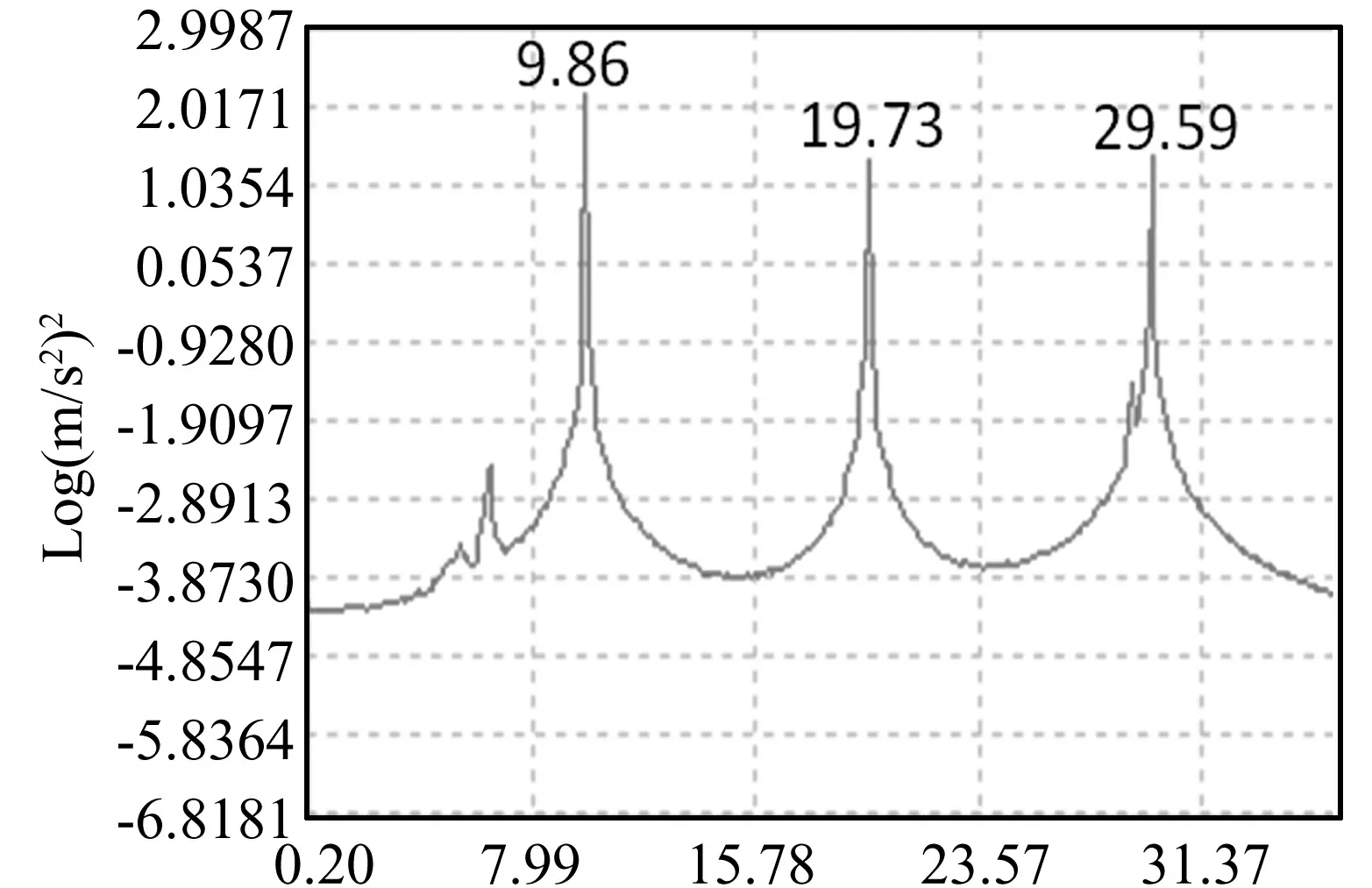
图7 在9.86 Hz处的功率谱Fig.7 Power spectrum when exciting frequency is 9.86 Hz
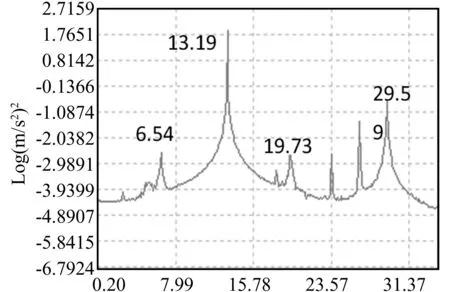
图8 在13.19 Hz处的功率谱Fig.8 Power spectrum when exciting frequency is 13.19 Hz
当激振频率为13.19Hz时,可以将结构的第一阶、第二阶和第三阶频率激发出来。
因此在组合共振中,组合频率对结构安全性和可靠性分析将产生影响。组合共振现象再次说明,非线性系统具有比线性系统更多的共振机会,同时表明,系统的响应绝不是各个激励引起的响应之和。
4 结 论
本文主要对一类三层结构模型进行了模态实验和非线性振动实验研究,得到如下结论:
(1) 该三层结构第一阶频率与第二阶频率之比接近1∶3。
(2) 水平基础激励下结构响应存在1∶3内共振现象,以一阶模态频率、二阶模态频率激励,都可激发出一、二阶模态间的内共振行为。
(3) 水平基础激励下结构响应中存在多种组合共振,其对结构振动所产生的影响是不可忽略的。
以上结论多层工程结构设计和健康监测有一定参考作用。
[ 1 ] 陈予恕. 非线性振动系统的分叉和混沌理论[M]. 北京:高等教育出版社,1993.
[ 2 ] Nayfeh A H,Pai P F. Linear and nonlinear structural mechanics[M]. New York: Wiley-Interscience,2002.
[ 3 ] 胡海岩. 应用非线性动力学[M]. 北京:航天工业出版社,2000.
[ 4 ] Malatkar P,Nayfeh A H. A plethora of nonlinear dynamics phenomena observed in a simple cantilever plate[C], ASME 2003 Design Engineering Technical Conferences,Chicago, llinois, USA 2003.
[ 5 ] Alhazza K A,Nayfeh A H, Daqaq M F. Delayed-acceleration feedback for active-multimode vibration control of cantilever beams[C].Proceedings of the ASME 2007 International Design Engineering Technical Conferences,Las Vegas, Nevada, USA 2007.
[ 6 ] Inoue T, Ishida Y. Chaotic vibration and internal resonance phenomena in rotor systems[J]. Journal of vibration and acoustics, 2005, 128(2): 156-169.
[ 7 ] Benedettini F, Alaggio R, Zulli D. Nonlinear coupling and instability in the forced dynamics of a non-shallow arch: theory and experiments[J]. Nonlinear Dynamics, 2012, 68(4): 505-517.
[ 8 ] 季进臣,陈予恕,叶 敏,等. 参激屈曲梁的倍周期分岔和混沌运动的实验研究[J]. 实验力学,1997,12(2):248-259. JI Jin-chen, CHEN Yu-shu, YE Min,et al. Experimental investigation on the period doubleling bifurcation and chaotic motions of a parametrically excited buckled beam[J]. Journal of Experimental Mechanics, 1997, 12(2):248-259.
[ 9 ] 刘习军,王大钧,陈予恕. 中华文物龙洗(鱼洗)有趣现象的非线性分析[J]. 科学通报,1996,41(5):413-417. LIU Xi-jun, WANG Da-jun, CHEN Yu-shu. Nonlinear analysis of the mystenous chinese antiquities dragon washbasin phenomenon[J]. Chinese Science Bulletin, 1996, 41(5): 413-417.
[10] 魏明海, 肖仪清.内外共振联合作用下索-梁组合结构非线性振动分析[J].振动与冲击, 2012, 31(7): 79-84. WEI Ming-hai, XIAO Yi-qing. Nonlinear vibration analysis for a cable-beam coupled system under simultaneous internal and external resonances[J]. Journal of Vibration and Shock, 2012, 31(7): 79-84.
[11] 孟 光,孟庆国,詹世革,等. 关于加强针对国家重大装备的动力学与控制研究的建议[J]. 力学进展,2007,37(1):135-141. MENG Guang, MENG Qing-guo, ZHAN Shi-ge,et al. Suggestion on the study of dynamics and control in key equipments[J]. Advances in Mechanics, 2007,37(1): 135-141.
Internal and combinational resonances of a three-story structure
WU Zhi-qiang1, CHEN Shi-dong1,2, LEI Na1,2, GONG Ming-xu1
(1. Department of Mechanics, School of Mechanical Engineering, Tianjin University, Tianjin 300072, China;2. Engineering Research Institute of Beijing FOTON CO., LTD., Beijing 102206, China)
Experiments for internal and combinational resonances of a three-story structure were investigated. The frequency ratio between the first and the second modes of the structure was set near 1∶3 with a modal design. The internal resonance behaviors were found when the excitation frequency was close to the first modal frequency or the second one. Meanwhile, several types of combinational resonances were found in this structure. These results laid a foundation for future modification of a nonlinear vibration equipment.
three-layer structure; internal resonance; combination resonance
国家自然科学基金( 11172198);教育部博士点基金(2009003211005);教育部新世纪优秀人才支持计划(NCET-15-0247)
2013-01-22 修改稿收到日期:2013-05-22
吴志强 男,教授,博士生导师,1968年生
TH212;TH213.3
A
10.13465/j.cnki.jvs.2014.08.001
