某菱形截面纪念碑风致气弹响应风洞试验研究

宋微微 ， 梁枢果 ， 邹良浩 ， 温四清

(1.武汉大学 土木建筑工程学院，武汉 430072；2.中信集团武汉市建筑设计院，武汉 430014)

某菱形截面纪念碑风致气弹响应风洞试验研究

宋微微1， 梁枢果1， 邹良浩1， 温四清2

(1.武汉大学 土木建筑工程学院，武汉 430072；2.中信集团武汉市建筑设计院，武汉 430014)

对某高100 m的菱形截面纪念碑进行刚性模型多点同步扫描测压与摆式气弹模型测振风洞试验，进而在测压数据基础上建立频域风荷载模型并采用随机振动分析方法计算结构风振响应，同时应用随机减量技术(RDT)识别了该气弹模型风致振动时的气动阻尼比。当在频响函数中考虑气动阻尼比后的风振响应计算结果和气弹模型试验值具有很好的一致性。由于实际结构振型与摆式模型线性振型存在差异，用振型修正系数修正气弹模型试验结果可得到实际结构风振响应。分析结果表明，刚性模型测压建立荷载模型，结合气弹模型测振识别气动阻尼，代入实际结构频域响应计算方法能够较精确地评估强风作用下低频小阻尼高耸结构的风致气弹响应。

纪念碑； 摆式气弹模型；风致气弹响应；气动阻尼比；线性振型

纪念碑是一种特殊的高耸结构，尤其是钢结构纪念碑具有高宽比大、频率低、阻尼小的特点，是典型的风敏感结构，在强风作用下极易产生大幅度振动。大量试验与实测数据显示[1]，对于频率低、阻尼小的高耸钢结构在强风下的风致振动评估应该考虑气动弹性效应，尤其是气动阻尼的影响。如忽略气动阻尼的影响，仅根据刚性模型风压测试数据计算高耸钢结构在强风作用下的风振响应，得到的结果与实际情况有较大的偏差[2-3]。

某钢结构纪念碑高100 m，截面为菱形。为了精确地评估该结构在强风作用下的风致气弹响应与抗风性能，本文作者采用刚性模型多点同步测压技术和双向摆式气弹模型测振技术对该纪念碑风致响应进行风洞实验研究。根据气动弹性模型试验数据，运用随机减量技术识别结构气动阻尼比，并且结合刚性测压模型的风荷载输入，基于频域随机振动理论计算了强风下考虑气动阻尼比的结构一阶线性振型顶部位移和加速度均方根响应，计算结果与气动弹性模型试验值有很好的一致性，证明该钢结构纪念碑在强风作用下的气动弹性效应不可忽略。在此基础上，对线性振型进行修正，可以得到较精确的该纪念碑结构风致气弹响应。

1 风洞实验概况

1.1 风场的模拟

本次试验在湖南大学HD-2风洞试验室第一试验段进行。该试验段长17 m，宽3 m、高2.5 m。采用档板、尖塔、粗糙元等装置来模拟大气边界层风场，本次试验模拟建筑结构荷载规范中的C类地貌，风剖面地面粗糙度指数α=0.22。在模型放置中心测得的风速剖面、湍流度剖面如图1(a)和图1(b)所示，湍流度剖面与我国荷载规范(GB50009-2012)比较吻合，边界层顺风向风速谱和 Karman 谱拟合较好，如图1(c)所示。

1.2 工程背景

某纪念碑为菱形截面双层钢结构体系，内筒各层平面不变，外筒自下而上逐渐收小。立面自下向上开有不规则的三角形镂空孔洞，外挂花岗岩石材。内筒设置景观电梯，顶部设置了三层观景平台。模型外观及风洞试验风向角定义见图2。

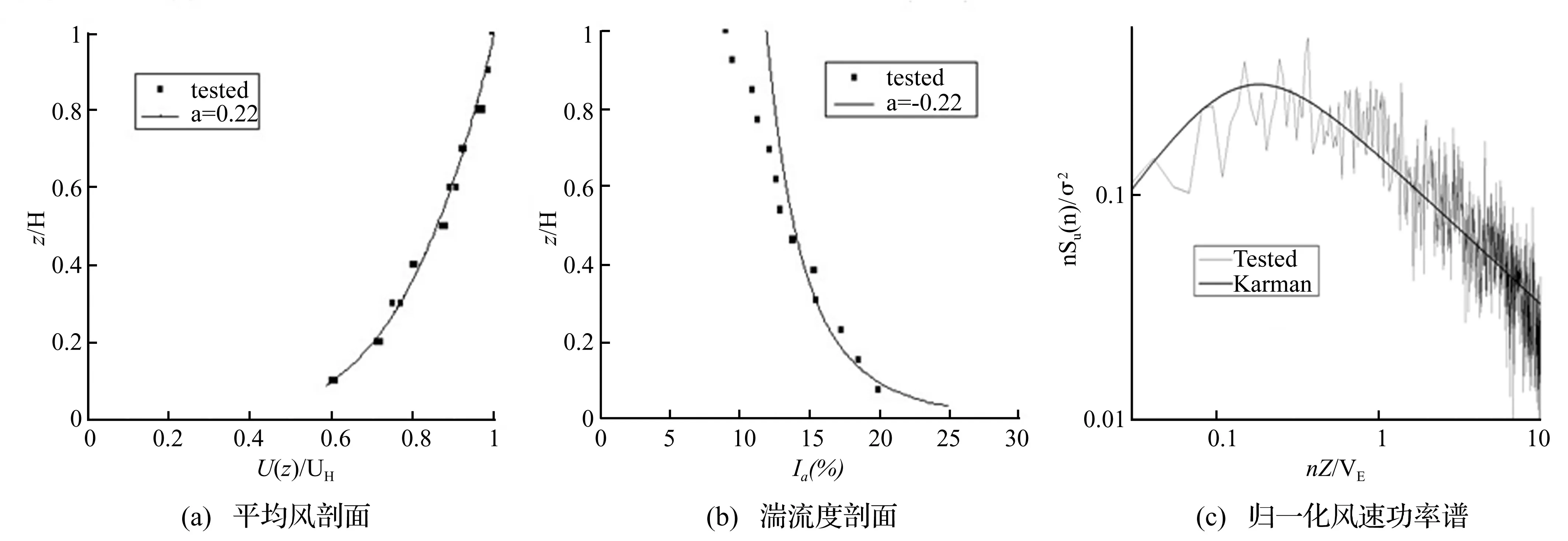
图1 风场模拟Fig.1 Wind field simulation

1.3 气弹模型试验设计

采用ANSYS软件的beam188单元建立结构有限元模型，进行模态分析得到原结构在X轴向和Y轴向振型互不耦联，一阶频率分别为0.65 Hz(X轴向)和0.73 Hz(Y轴向)，图3为实际结构X轴向和Y轴向第一振型曲线。由于结构振型稀疏，根据刚性模型同步测压试验的分析结果显示，风振位移响应的X轴向和Y轴向一阶模态响应的能量占各阶模态动态位移总响应能量的99%以上，表明该结构的风振响应是由基阶模态控制的，因此双向摆式气弹模型可以满足工程精度要求。试验风速为2 -11 m/s(对应实际风速为20 -110 m/s)。

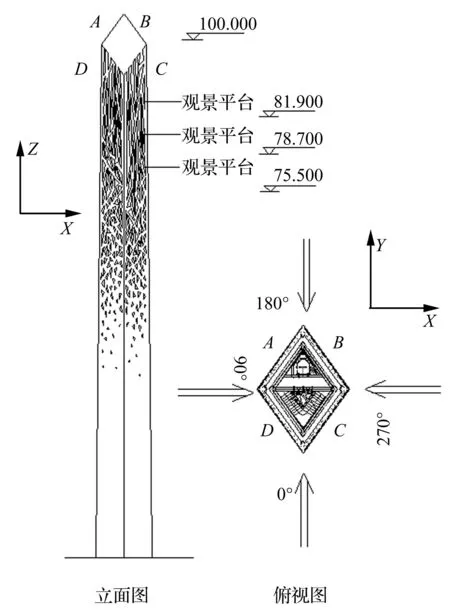
图2 试验模型及风向角示意图Fig.2 Test model and wind direction diagram

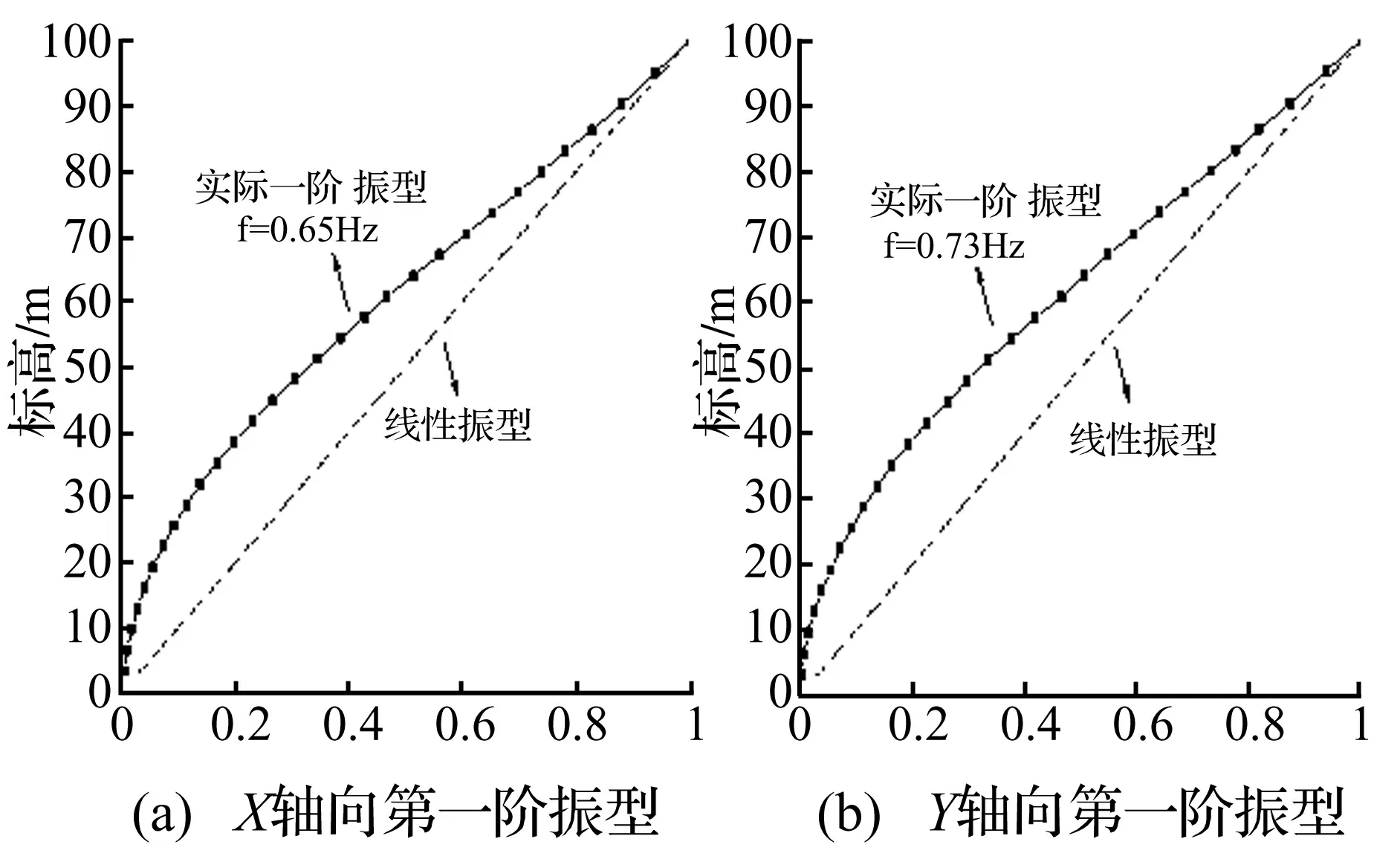
图3 实际结构基阶振型曲线Fig.3 Structural X axial and Y-axial mode shape and frequency

气弹模型几何缩尺比取1∶100，进而根据相似理论可以确定其他参数的相似比值(表1)。对于小振幅摆动，质量相似只需模拟结构绕基底的转动惯量。原结构的转动惯量为3.10×109kg·m2，气弹模型重652 g，计算得1.0 kg配重质量块的位置在距离万向节转动中心40 cm处。正交方向上的四根弹簧模拟结构侧向弯曲变形刚度，X轴向、Y轴向弹簧的弹性系数设计值分别为1 130.6 N/m和1 432.1 N/m，选用型号d×D2×L=2×18×27和2×18×100的拉伸弹簧，弹性系数经标定，与预期值非常接近。由建筑结构荷载规范[4]结构阻尼比取0.01，气弹模型系统的阻尼比通过反复调节阻尼片浸入油池的深度来实现。图4为气弹模型底部支撑系统的设计构造图。为避免测量仪器对流场的干扰，加速度传感器和激光位移计放置在风洞地面以下离转轴21.1 cm处，分别测量X轴向和Y轴向的加速度和位移响应。

表1 摆式气弹模型的相似比值

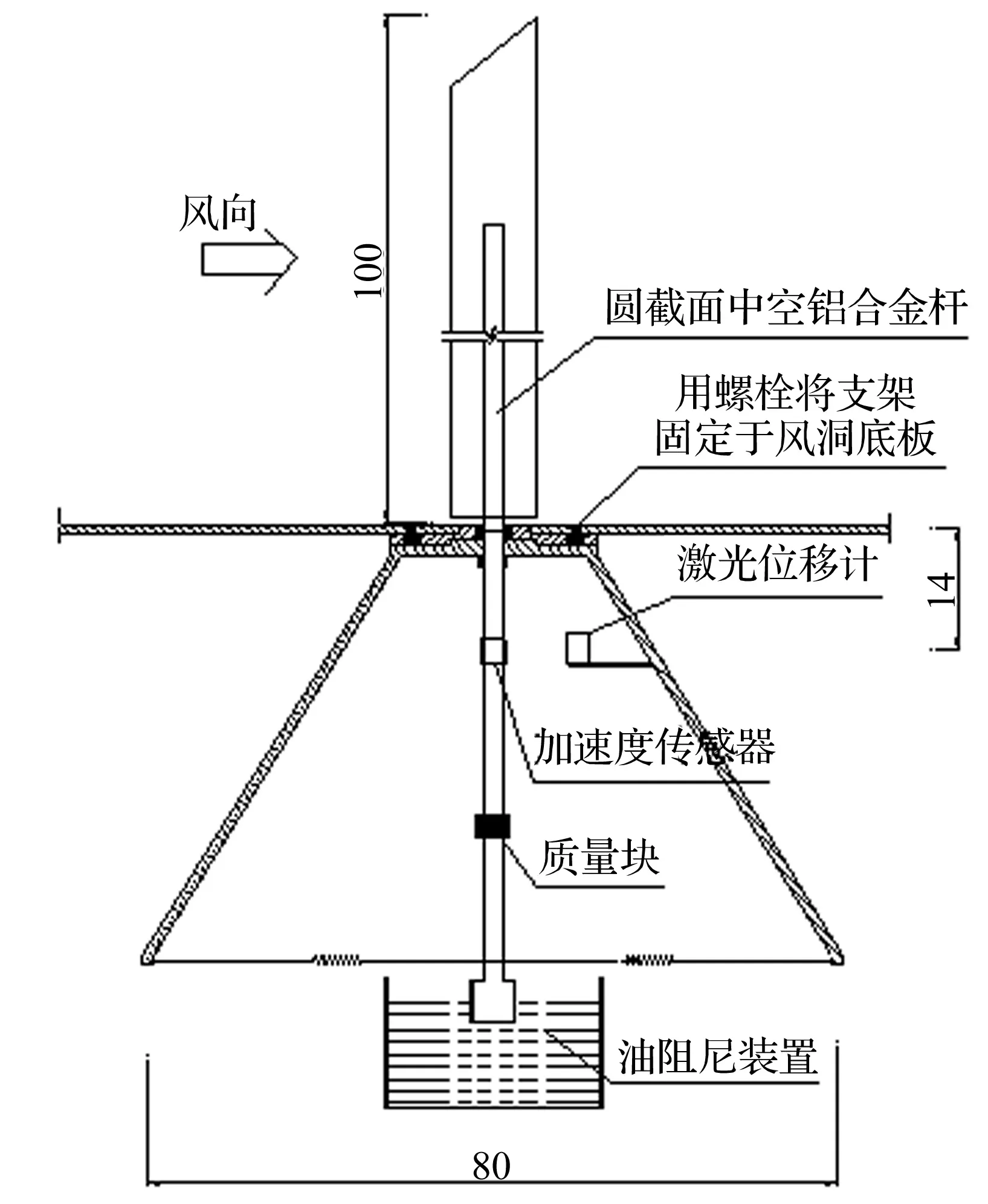
图4 气弹模型装置示意图Fig.4 Aero-elastic model device diagram

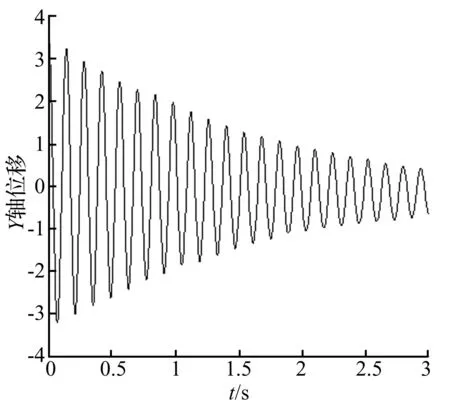
图5 自由振动测试Fig.5 Free vibration test

吹风前，进行敲击试验得到结构两个主轴向的有阻尼自由振动衰减曲线，进行FFT变换得到气弹模型的X轴向和Y轴向一阶固有频率分别为6.3 Hz和7.2 Hz,自由振动测试结果见图5。根据基于自由振动衰减曲线的阻尼比计算公式:

(1)

计算的X轴向和Y轴向一阶模态结构阻尼比分别为0.009 5和0.009 3;与设计值误差都在10%以内。式中，Am，An+m分别为第m和第m+n个波形振幅，n为波形个数。

2 试验数据处理

2.1 随机减量法

本文通过摆式气弹模型风洞试验测得结构两个主轴向的一阶位移和加速度响应，采用随机减量技术[5-6]识别了结构的一阶气动阻尼比。随机减量方法(RDT)的基本原理是利用样本平均法，去掉样本中的随机成分，获得一定初始激励下振动系统的自由衰减响应，由此计算得到系统的阻尼比。为了消除响应信号中混杂的低频和高频分量，使用带通滤波器对响应信号进行预处理。滤波器上下截止频率依据结构固有频率进行选取。利用随机减量技术识别出模型在风场中振动的一阶总阻尼比ξ1，减去自由振动得到的一阶结构阻尼比ξs1即得到一阶气动阻尼比ξa1=ξ1-ξs1

2.2 频域风振响应计算方法

本次气弹模型试验在典型风向角下，试验风速范围内结构X轴向、Y轴向响应时程曲线都为随机过程。依据随机振动理论[7]，广义荷载谱和广义质量由下式计算得到：

(2)

(3)

式中,Sk(z,n)为实际结构荷载谱密度函数，由刚性模型测压实验数据，经面积加权平均得到[8]，φi(z)为第i振型的振型函数。

结构沿x轴向、y轴向第i阶振型位移均方根响应和加速度均方根响应由下式计算：

k=x,y

(4)

k=x,y

(5)

采用SRSS方法计算各轴向最大动态位移响应和最大加速度响应为

(6)

(7)

式中，μ为峰因子，按99.8%的保证率，取3。

(8)

为第i振型频响函数。

该结构在X轴向和Y轴向二阶模态频率已分别达到2.91 Hz和3.41 Hz, 如前述，二阶以上的各高阶模态对该结构X轴向和Y轴向动态位移及加速度的贡献都不大，仅考虑一阶模态的贡献就可以达到较高的精度。同时，在表面风压测试数据的基础上对该结构的扭转风振响应进行了分析，显示扭转振动对该结构的风振响应贡献极小，可略去不计。

结构的气弹效应包括气动质量、气动刚度和气动阻尼。分析表明[9-10]，对于高层、高耸结构，气动质量和气动刚度的影响很小可忽略，在表达式(8)中令i阶模态阻尼比ξi=ξis+ξia,则计算结果为考虑气弹效应的风振响应，如令ξi=ξis，则计算结果为不考虑气弹效应的风振响应，式中ξis,ξia分别为i阶模态结构阻尼比和气动阻尼比。

3 试验结果分析

气弹模型风洞试验现象观测显示，在试验风速范围内，各风向角气弹模型均未发生涡激共振现象。通过分析风振响应均方根得到，两个主轴向均方根响应随风速增加单调递增，没有出现明显共振峰；0°风向角横风向风振响应大于顺风向风振响应，90°风向角顺风向风振响应大于横风向风振响应，其他风向角同样是X轴向响应大于Y轴向响应，X轴向与Y轴向的均方根风振响应比值都在2以内。

3.1 气动阻尼比分析

由上述方法识别的气动阻尼比随折算风速的变化曲线见图6。横坐标V/n0D表示折算风速,V为参考点风速,n0为该轴向的固有频率,D为迎风面投影宽度。由图可见，不同风向角的X轴向和Y轴向气动阻尼比在折算风速20以内都为正值，绝大部分值都位于0-0.05之间。0°风向角，气动阻尼比在折算风速4附近出现峰值以后，气动阻尼比急剧降低，折算风速达到7时，顺风向气动阻尼比随风速的变化趋于平缓，横风向气动阻尼比缓慢增大，直到折算风速大于16以后，横风向气动阻尼比回落；90°风向角，气动阻尼比在折算风速4附近出现峰值以后，顺风向气动阻尼比趋于平缓，横风向气动阻尼比随风速增加急剧降低。在100年重现期极值风速作用下，90°风向角的气动阻尼比明显大于其他风向角的气动阻尼比。

因为识别的气动阻尼比跳跃性比较大，为便于工程应用取值，对各个风向角的气动阻尼比做多项式回归拟合分析，经反复筛选，取四次多项式拟合气动阻尼比。

ξa=a1(V/n0D)4+a2(V/n0D)3+

a3(V/n0D)2+a4(V/n0D)+a5

(9)

其中待定系数a1～a5用最小二乘法拟合得到。

对各风向角拟合得到的气动阻尼比参数见表2。

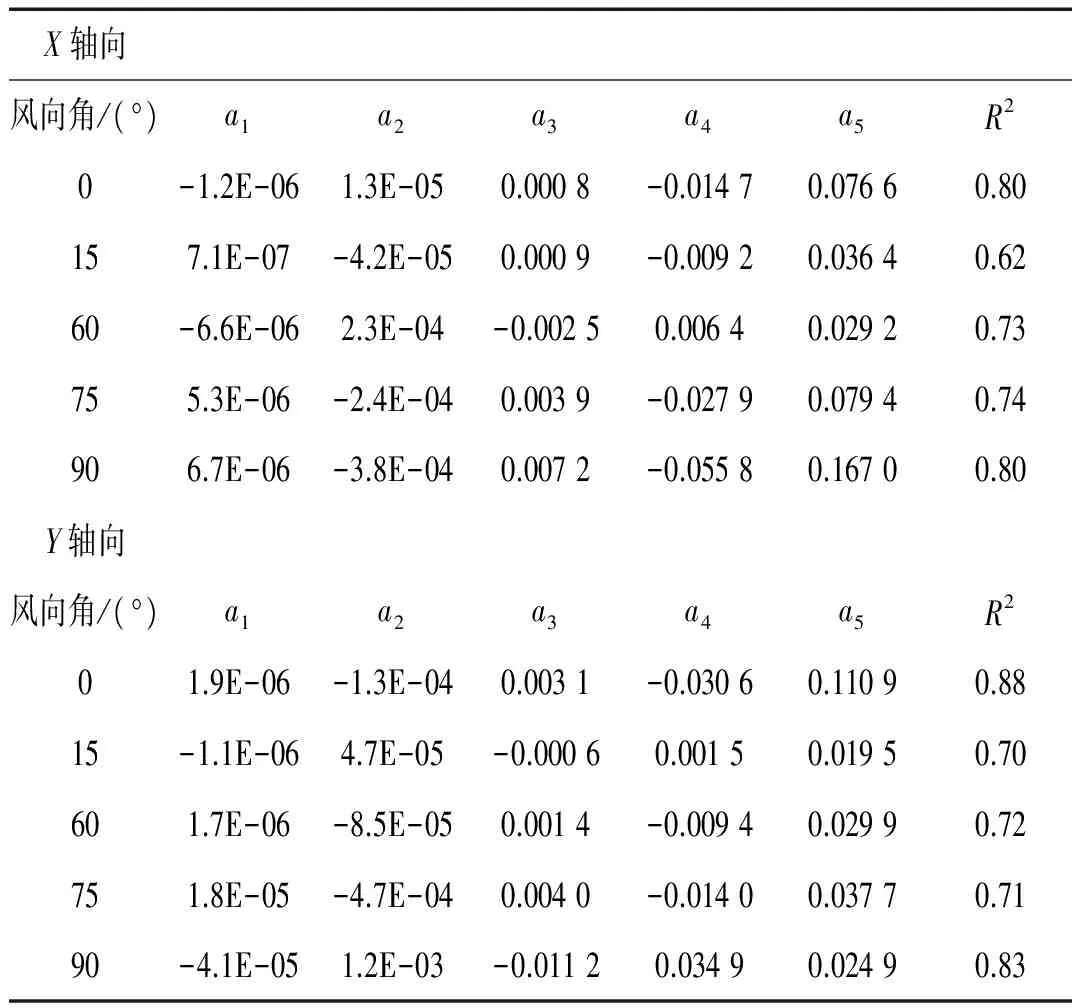
表2 纪念碑气动阻尼比参数拟合结果

为检验回归效果，定义复相关系数R2为

(10)

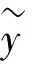
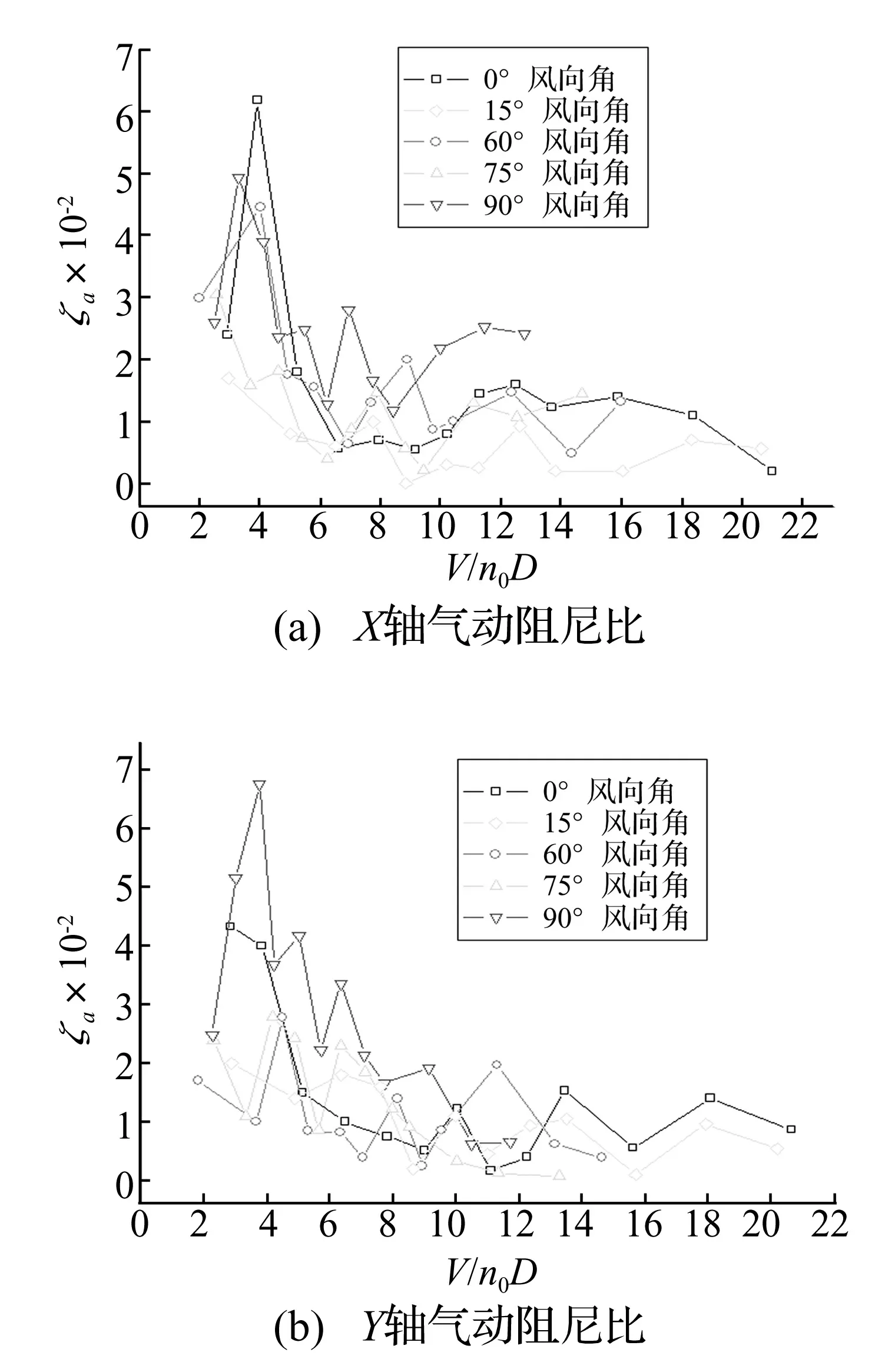
图6 气动阻尼比随折算风速的变化图Fig.6 Aerodynamic damping ratios versus reduced wind velocities

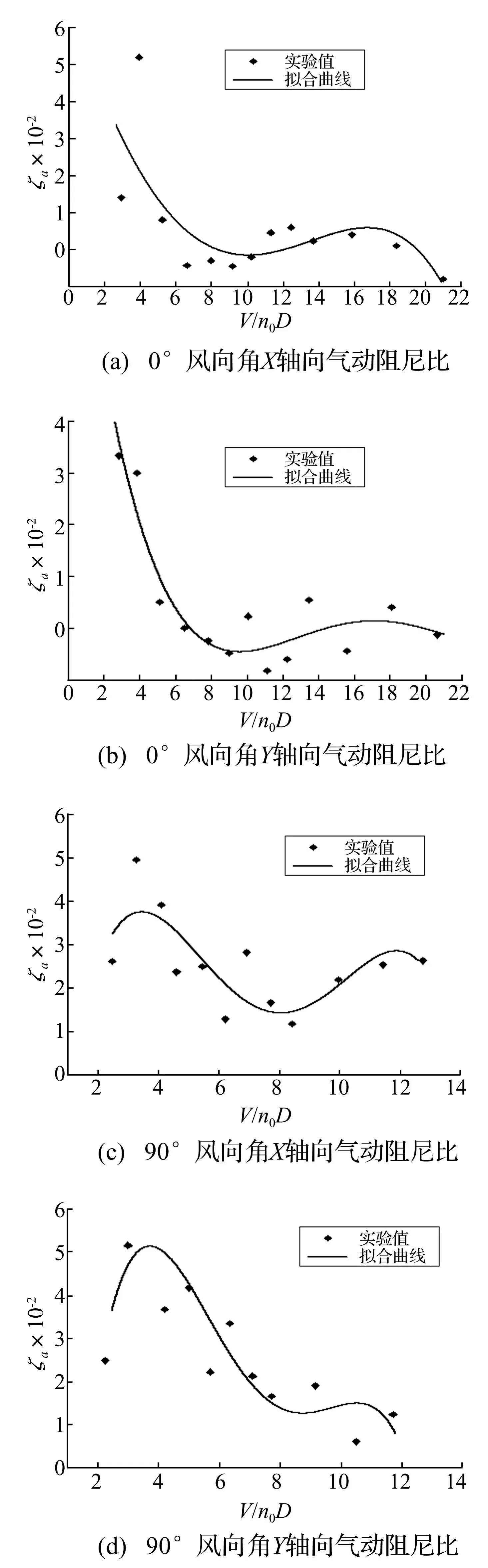
图7 气动阻尼比拟合结果Fig.7 Fitting results of aerodynamic damping ratios

3.2 气动阻尼对风振响应的影响

为研究气动阻尼对结构风振响应的贡献,采用上述频域计算方法，在频响函数中分别考虑气动阻尼比和不考虑气动阻尼比计算结构顶部位移和加速度均方根响应，并与气弹模型试验值比较。图8-图13分别给出0°、90°和60°风向角顶部位移和加速度均方根响应比较图。实线表示气弹模型实验值。从图中可以看出，采用实际结构第一振型、结构阻尼比计算结果，与气弹模型实验值差别比较大;当考虑气动阻尼比后，得到的计算结果减小很多，与气弹模型实验值更接近;当考虑了气动阻尼比，并且第一振型采用线性振型的计算结果，与气弹模型实验值具有相当好的一致性。在60°风向角，风向与截面边长接近垂直。X轴和Y轴的气动阻尼比对风振响应的影响相当。90°风向角，气动阻尼比对风振响应的影响最明显，因为90°风向角的气动阻尼在大部分风速范围内大于其他风向角。从图8-图13很容易看出，气动阻尼比对加速度响应的影响比对动态位移响应的影响更大。其他风向角的情况类似，在此不一一列举。图14所示为该纪念碑观景平台在不同风向角10年一遇极值风速作用下，考虑和不考虑气动阻尼比的加速度响应计算结果比值。图15所示为该纪念碑顶部在不同风向角100年一遇极值风速作用下，考虑和不考虑气动阻尼比的位移均方根响应计算结果比值(计算式为公式(11)、(12))。由图14、图15可见，考虑气动阻尼后，加速度均方根响应降低35%-60%，位移均方根响应降低20%-40%。对该纪念碑钢结构而言，不考虑气动阻尼，会严重高估结构的风振响应，使设计偏保守。

Ratioacc=

(11)

Ratiodisp=

(12)

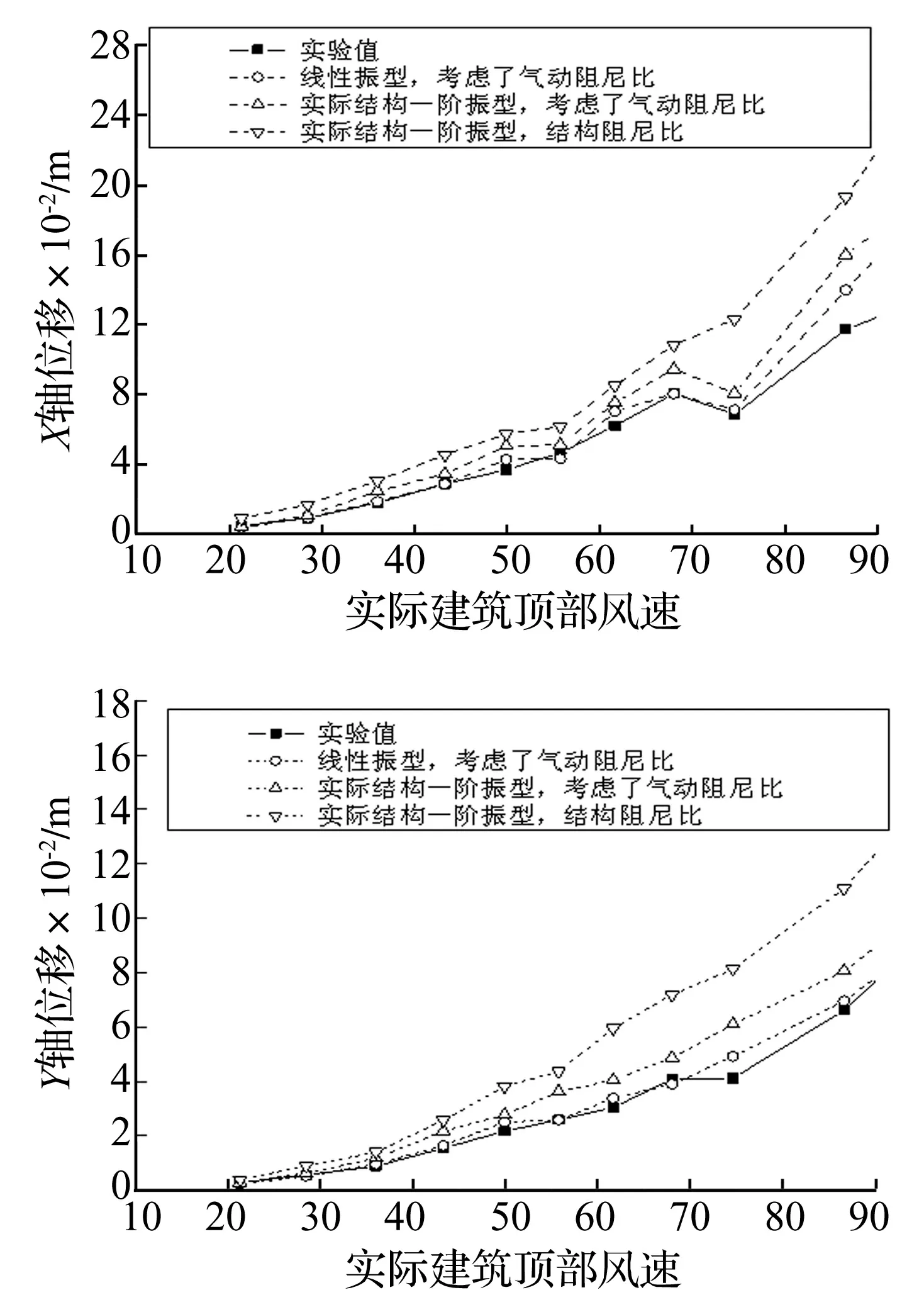
图8 0°风向角顶部位移均方根响应图Fig.8 The top displacement RMS response versus reduced wind velocities at wind direction of 0 degree

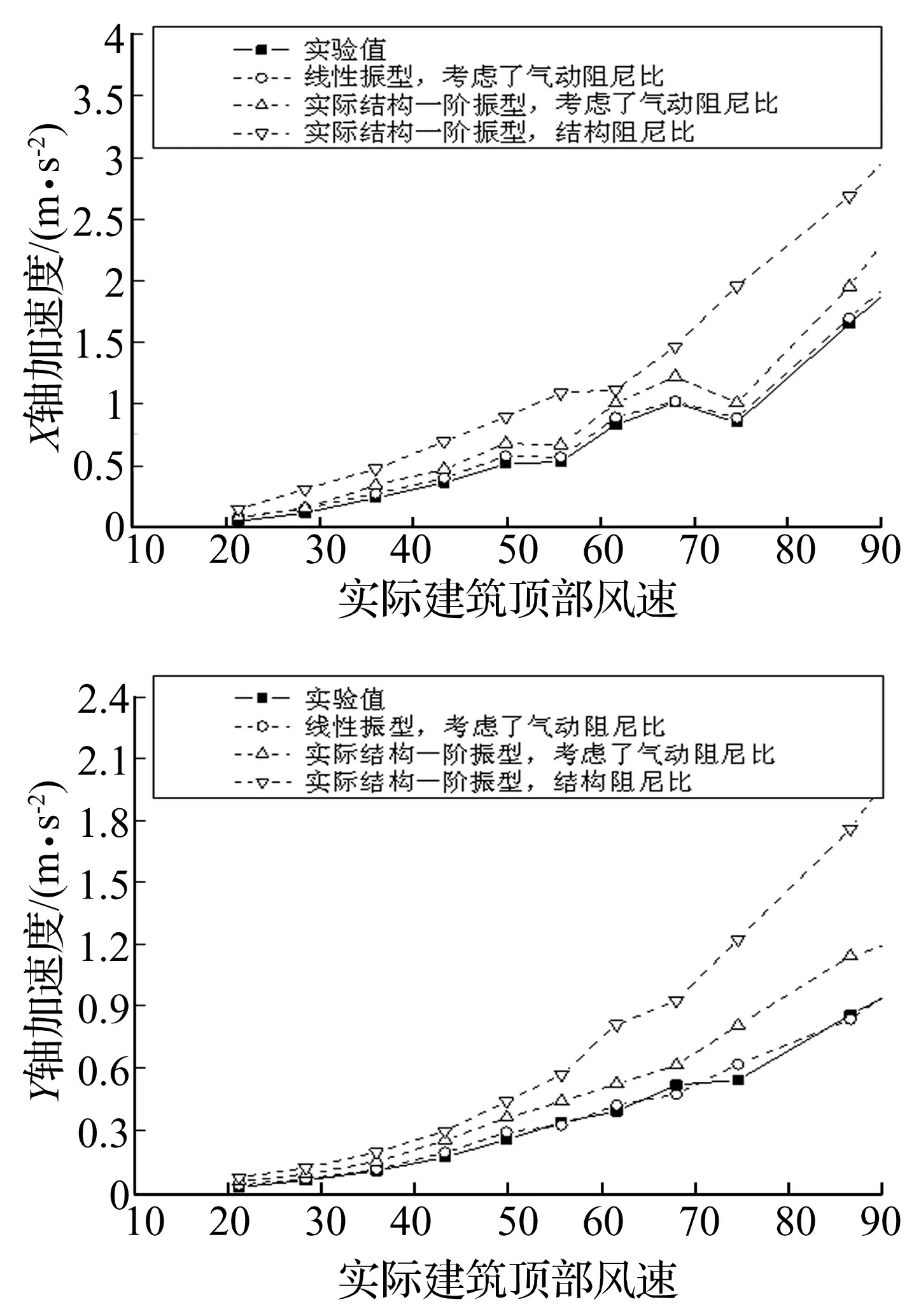
图9 0°风向角观景平台加速度均方根响应图Fig.9 The viewing platform acceleration RMS response versus reduced wind velocities at wind direction of 0 degree

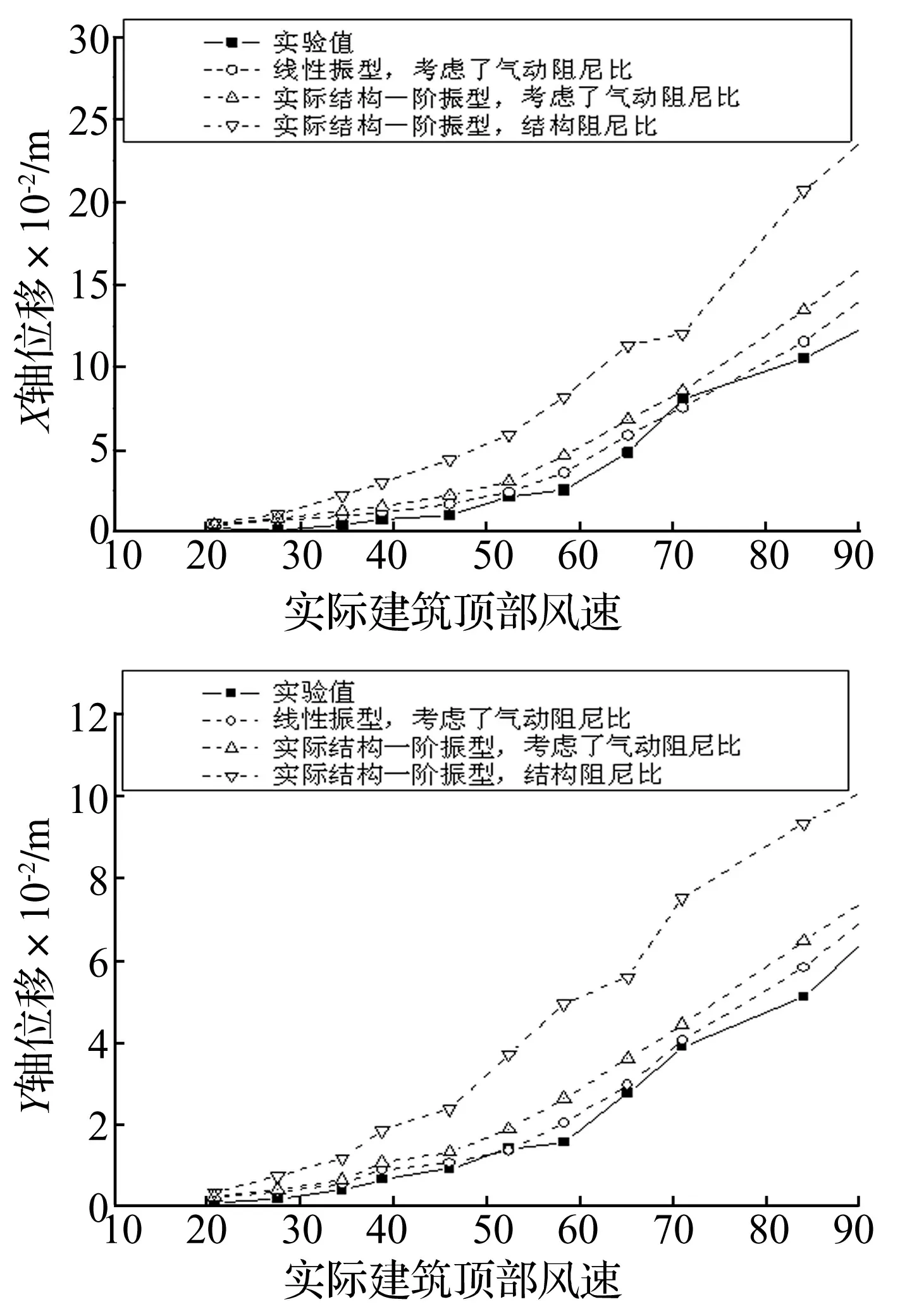
图10 90°风向角顶部位移均方根响应图Fig.10 The top displacement RMS response versus reduced wind velocities at wind direction of 90 degree

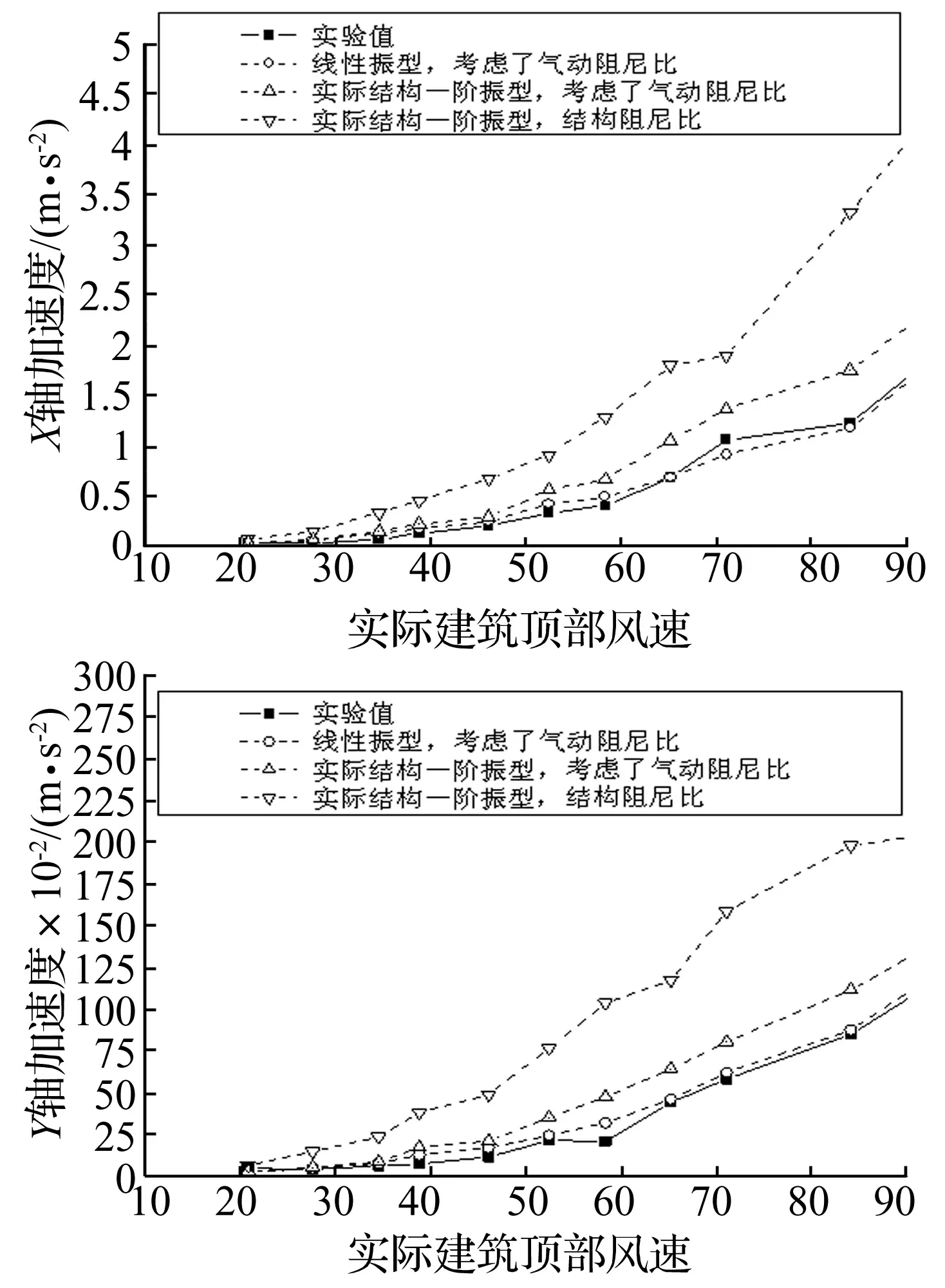
图11 90°风向角观景平台加速度均方根响应图Fig.11 The viewing platform acceleration RMS response versus reduced wind velocities at wind direction of 90 degree

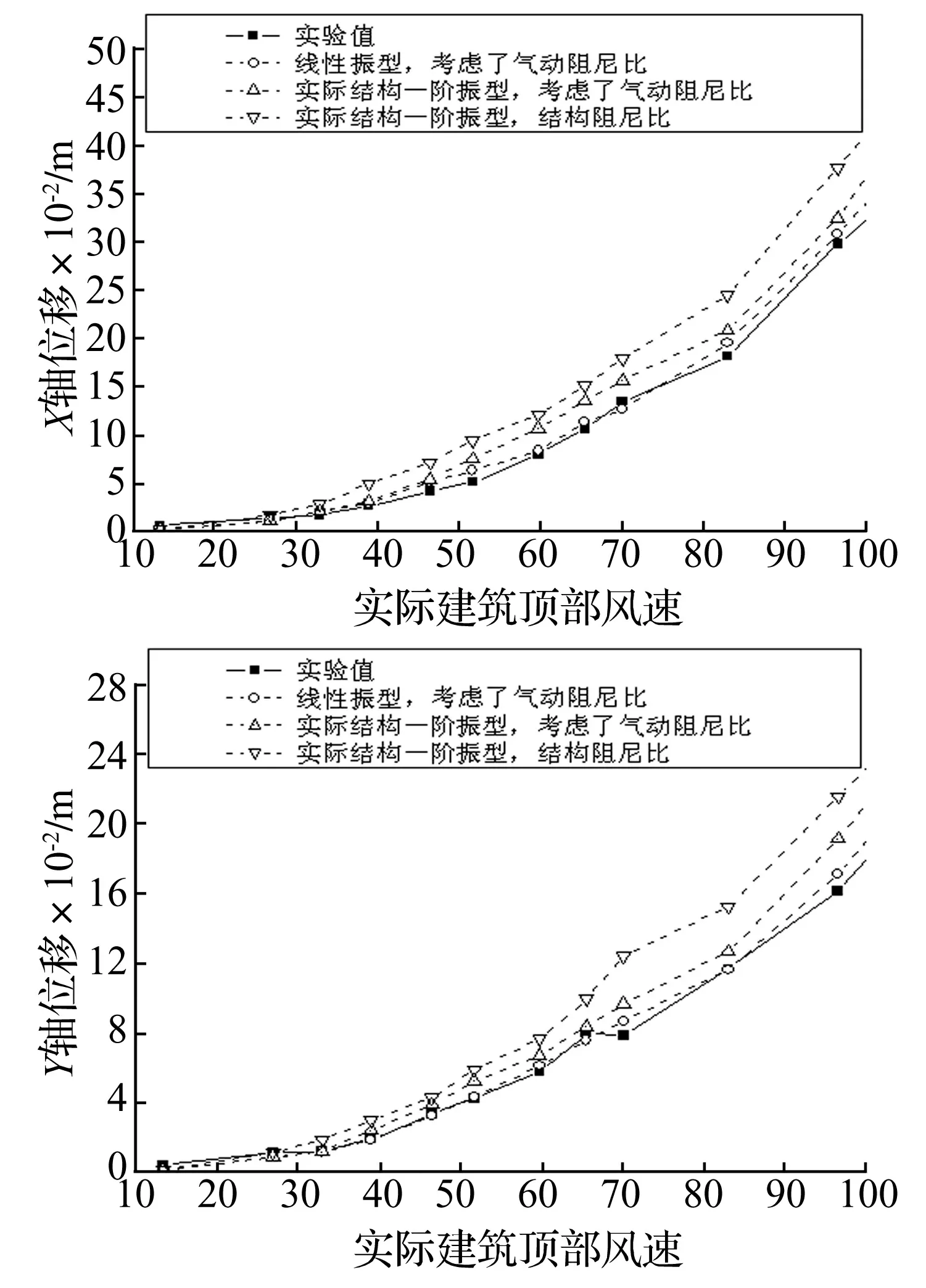
图12 60°风向角顶部位移均方根响应图Fig.12 The top displacement RMS response versus reduced wind velocities at wind direction of 60 degree

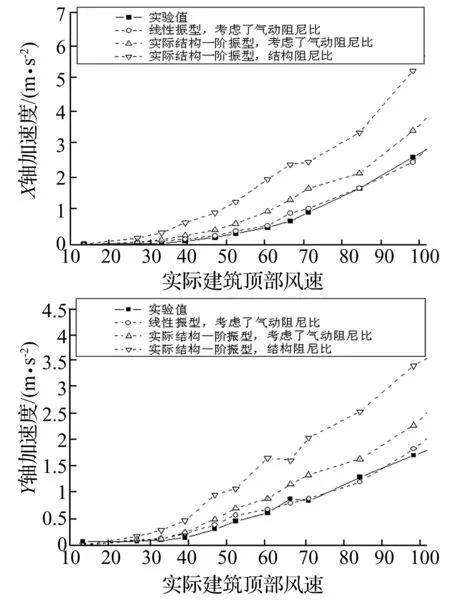
图13 60°风向角观景平台加速度均方根响应图Fig.13 The viewing platform acceleration RMS response versus reduced wind velocities at wind direction of 60 degree

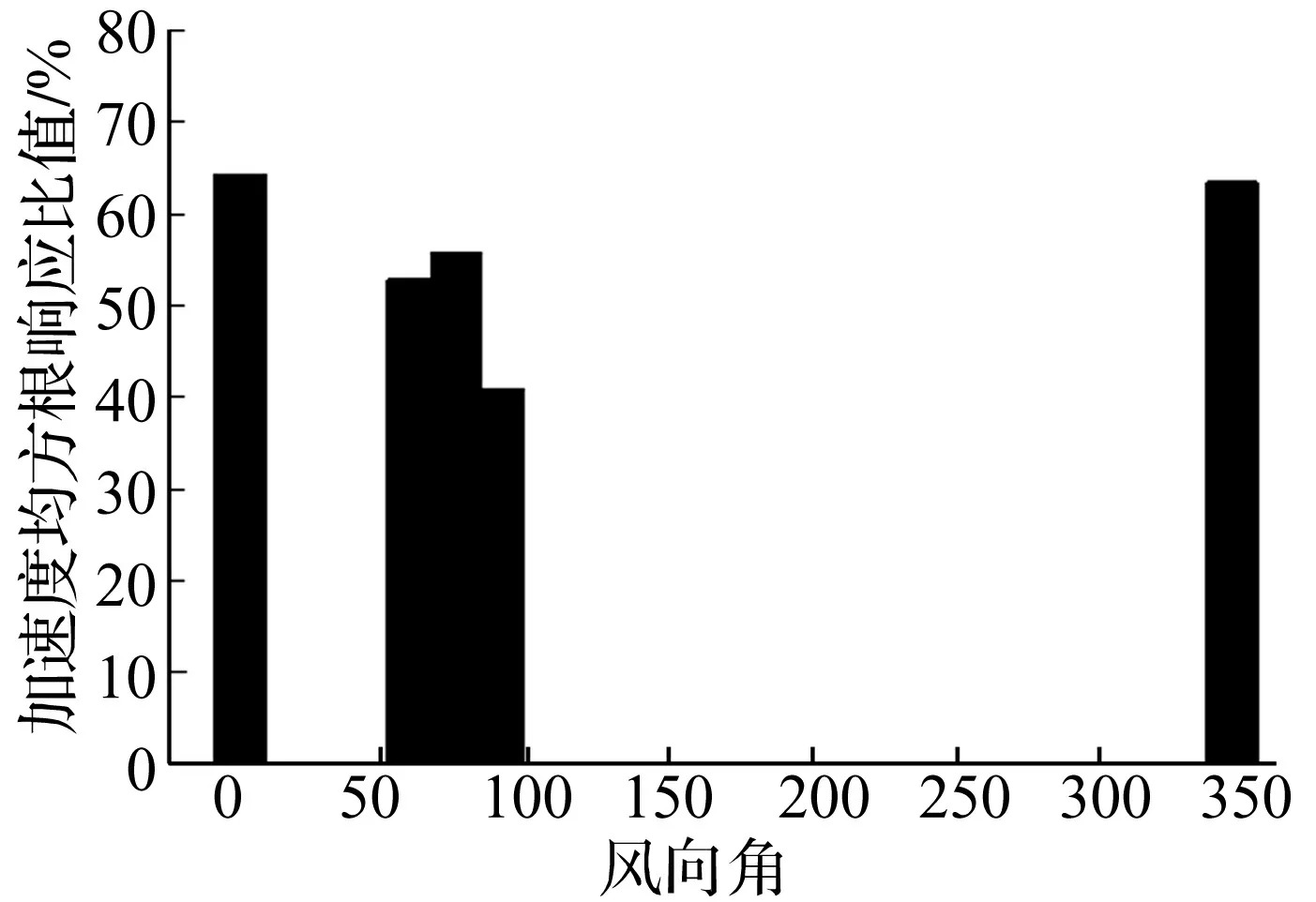
图14 考虑气动阻尼比和未考虑气动阻尼比加速度均方根响应比值图Fig.14 The ratios of acceleration RMS responses with and without aerodynamic damping

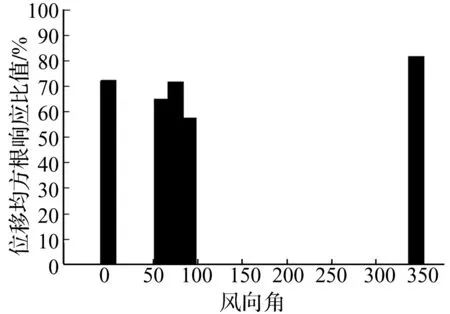
图15 考虑气动阻尼比和未考虑气动阻尼比位移均方根响应比值图Fig.15 The ratios of displacement RMS response with and without aerodynamic damping

3.4 线性振型修正系数

从图8-图13可以看出振型对风振响应有20%左右的影响。由于摆式气弹模型将结构一阶振型简化为线性振型，实际结构基阶弯曲振型与线性振型差别较大时，必须对摆式气弹模型测得的响应进行修正得到实际结构的响应[11]。本文定义修正系数(correction factor )为

k=x,y

(13)

k=x,y

(14)

修正系数随风速增大而增大，在100年重现期极值风速作用下，典型风向角下的气弹模型的振型修正系数见表3(加速度为最高观景平台的加速度响应，位移为结构顶点的位移均方根响应)。

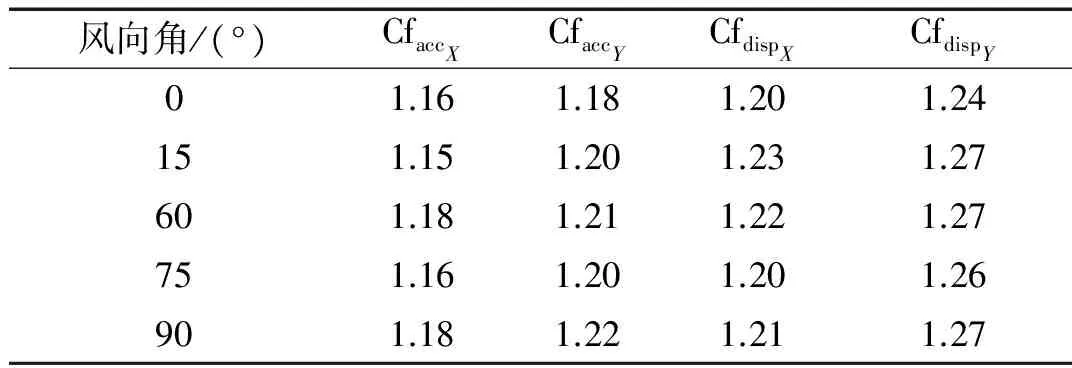
表3 摆式气弹模型的振型修正系数

由上表分析可得，该结构各风向角100年重现期极值风速下风振响应振型修正系数在1.15-1.28之间。位移响应振型修正系数略大于加速度响应振型修正系数，位移振型修正系数在1.24左右，加速度振型修正系数在1.18左右。

4 结 论

在刚性模型测压和双向摆式气弹模型风洞试验数据上，对某菱形截面钢结构纪念碑的气弹风振响应进行对比分析，得出以下主要结论：

(1) 对钢结构纪念碑这类高宽比大、结构阻尼小、频率低的高耸结构，气动阻尼比对结构风振响应，特别是对加速度响应的影响很大，仅根据刚性模型测压得到风荷载，不考虑气动阻尼比的风振响应计算结果严重失真，通常情况下可高估风振响应20%-60%。

(2) 通过摆式气弹模型风洞试验数据识别气动阻尼，代入刚性模型测压基础上的频域风振响应计算方法，相同参数下得到的计算结果与摆式气弹模型风振响应试验值吻合相当好。因此，通过摆式气弹模型试验对不同截面的钢结构高耸结构在典型风场中各工况下的双轴向气动阻尼进行识别和回归分析，可提出具有一定普遍性的气动阻尼计算公式，用于高耸钢结构的抗风设计。

(3) 对于一阶模态对风振响应的贡献占统治地位的高耸钢结构，双向摆式气弹模型风洞试验结果考虑振型修正系数后，可以用于实际工程抗风设计。对于本文中的菱形钢结构纪念碑，100年重现期风荷载下，加速度振型修正系数在1.18左右，位移振型修正系数在1.24左右。

(4) 本文的分析表明，刚性模型测压建立荷载模型，结合气弹模型测振识别气动阻尼，代入实际结构频域响应计算方法能够较精确地评估强风作用下低频小阻尼高耸结构的风致气弹响应。

[ 1 ] Taniike Y, Inaoka H. Aeroelastic behavior of tall buildings in wakes [J]. Journal of Wind Engineering And Industrial Aerodynamics,1988, 28(1-3): 317-327.

[ 2 ] 黄鹏，顾明. 高层建筑干扰气动阻尼的试验研究[J]. 同济大学学报,2003, 31(6): 652-656. HUANG Peng, GU Ming. Experimental study on aerodynamic damping of tall buildings after being interfered[J].Journal of Tongj I University,2003, 31(6): 652-656.

[ 3 ] 王辉. 气动阻尼对高层建筑横风向风振响应的影响[J].力学与实践,2007, 29(5): 38-42. WANG Hui. Effect of aerodynamic damping in across-wind dynamic responses of tall buildings[J]. Mechanics and Practice,2007, 29(5): 38-42.

[ 4 ] 建筑结构荷载规范(GB50009-2012)[S].北京, 2012.

[ 5 ] Tamura Y, Suganuma S Y. Evaluation of amplitude-dependent damping and natural frequency of buildings during strong winds[J]. Journal of Wind Engineering And Industrial Aerodynamics,1996, 59(2-3): 115-130.

[ 6 ] Marukawa H, Kato N, Fujii K, et al. Experimental evaluation of aerodynamic damping of tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics,1996, 59(2-3): 177-190.

[ 7 ] 欧进萍,王光远. 结构随机振动[M]. 北京: 高等教育出版社，1998.

[ 8 ] 梁枢果,邹良浩,郭必武. 基于刚性模型测压风洞试验的武汉国际证券大厦三维风致响应分析[J].工程力学,2009, 26(3):118-127. LIANG Shu-guo, ZOU Liang-hao,GUO Bi-wu. Investigation on wind-induced 3-D responses of Wuhan international stock building based on wind tunnel tests of rigid odels[J].Engineering Mechnics,2009, 26(3):118-127.

[ 9 ] Vickery B J, Steckley A. Aerodynamic damping and vortex excitation on an oscillating prism in turbulent shear flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49(1-3): 121-140.

[10] 吴海洋.矩形截面超高层建筑涡激振动风洞试验研究[D]. 武汉:武汉大学,2008.

[11] Xu Y L, Kwok K C S. Mode shape corrections for wind tunnel tests of tall buildings[J]. Engineering Structures,1993,15(5): 387-392.

Wind-induced aero-elastic responses of a monument with a rhombic cross-section

SONG Wei-wei1, LIANG Shu-guo1, ZOU Liang-hao1,WEN Si-qing2

(1.School of Civil Engineering and Architecture，Wuhan University, Wuhan 430072，China；2.Wuhan Architectural Design Institute, Wuhan 430014，China)

Wind tunnel tests of surface pressure scanning with a rigid model and vibration measurement with a stick-like aero-elastic model for a 100-meter-high monument with diamond-shaped cross-section were conducted, and then its frequency domain wind load model was established based on the pressure measurement data and the wind-induced response of the structure was calculated with the method of random vibration theory. Meanwhile, the aerodynamic damping ratio were identified by applying the random decrement technique (RDT). When the aerodynamic damping ratios were considered in the structural complex frequency response function, the calculation results of the wind-induced dynamic responses agreed well with the aero-elastic model test ones. Due to the difference between the structural actual modal shape and the linear modal shape of the stick-like aero-elastic model, modal shape correction factors were adopted to modify the aero-elastic model test results, and then the actual structural responses were acquired. The analysis results showed that the frequency domain response analysis method of a actual high-rise structure with a wind load model established using the surface pressure scanning test of a rigid model, combined with an aerodynamic damping identification using the aero-elastic model vibration measurement test, can be used to accurately assess the wind-induced aero-elastic responses of high-rise structures with low frequency small damping under strong wind actions.

monument; stick-like aero-elastic model; wind induced aero-elastic response; aerodynamic damping ratio; linear modal shape

国家自然科学基金项目(50678137)

2013-03-05 修改稿收到日期：2013-05-15

宋微微 女，博士生，1987年生

梁枢果 男，教授，博士生导师，1950年生

TU393. 2；TU317+.1

A

10.13465/j.cnki.jvs.2014.08.016