(Pa-U)模型下的二行动线性决策的贝叶斯假设检验

王燕飞，杨沐华

(1.吉林化工学院理学院，吉林吉林132022;2.吉林石化公司乙二醇厂，吉林吉林132022)

由式(1)及(3)，行动a2的后验风险为

关于假设检验问题，经典统计只研究了正态总体的情况.这种局限性主要是由于其需要构造枢轴量及涉及的抽样分布的复杂性.因此，对于总体分布为非正态分布时，经典统计就无能为力了.而贝叶斯统计恰好弥补了这个缺憾.在贝叶斯统计中，只要给出先验分布和总体分布形式，后验分布总是容易求得的.基于后验分布的贝叶斯假设检验问题就相对应用较广.对于这一类问题，已经有些研究者得出了一些研究成果.文献［1］对比了贝叶斯统计与经典统计的方法.文献［2］推出了新的二项分布的贝叶斯假设检验方法.文献［3］研究了总体为几何分布，负二项分布，威布尔分布和瑞利分布的未知参数的贝叶斯假设检验问题.文献［4］研究了三类非正态总体指数分布、二项分布和泊松分布的未知参数的贝叶斯假设检验，给出了相应的否定域.

无论贝叶斯决策论，还是经典决策论都认为，状态集Θ ={θ}，行动集A={a}和损失函数L(θ，a)是描述决策问题的3个基本要素.但两种决策论主要有2点不同:1.经典决策问题只利用抽样信息，而贝叶斯决策问题除了利用抽样信息以外，还用先验信息;2.在做决策时两种决策论所定义的期望损失不同.经典决策论中定义的是风险函数，即损失函数对样本分布的期望值.而贝叶斯决策论中，分别利用先验分布和后验分布计算期望损失，即先验期望损失和后验期望损失(后验风险).贝叶斯假设检验问题实质上也是一类决策问题.

在贝叶斯决策问题中，如果先验分布，总体分布形同，但损失函数不同，那么所得到的决策问题仍不同.在实际应用中，我们经常会遇到总体服从均匀分布的情况.而帕累托分布可用来描述诸如个人收入、某种药理过程后病人的存活时间等，被广泛地应用于经济学、保险损失、网络流建模、可靠性研究等领域，非常具有研究价值.本文研究了在总体分布为均匀分布，先验分布为帕累托分布的(Pa-U)模型下，对二行动线性决策问题作出贝叶斯假设检验的分析.这对于经营管理者作出较为合理的决策提供了统计依据.

1(Pa-U)模型

后验分布综合了先验信息，总体信息，样本信息3种信息，贝叶斯的统计推断和统计决策问题都是基于后验分布进行分析的.

2 (Pa-U)模型的二行动线性决策的贝叶斯假设检验

2.1 二行动线性决策的假设检验

设有H0:θ＞θ0，H1:θ≤θ0两个假设，两个行动a1，a2:a1表示接受H0的行动，a2表示接受H1的行动.即决策者认为，如果θ＞θ0，行动a1适宜;如果θ≤θ0，则行动a2最好.状态θ可以是离散或连续的;收益函数对每个行动都是状态参数的线性函数.即收益函数

不妨设m1＞m2，b1＜b2，保证θ0＞0.若m1＜m2，将a1与a2互换即可.

根据公式，有:行动ai的损失函数为L(θ，ai)=maax Q(θ，a)-Q(θ，ai)，得:

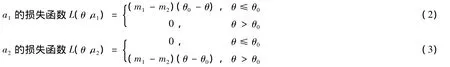
2.2 (Pa-U)模型的假设检验

即后验风险表示把损失函数L(θ，a)对后验分布π(θ|x)求期望，是用后验分布求得的平均损失［5］.它在样本x给定下，不同的行动a有不同的后验风险.而在行动a固定下，样本x的变化也会使后验风险随之变化.对于决策者来说，我们希望找到最有行动，使得后验风险达到最小.

由式(1)及(2)，行动a1的后验风险为

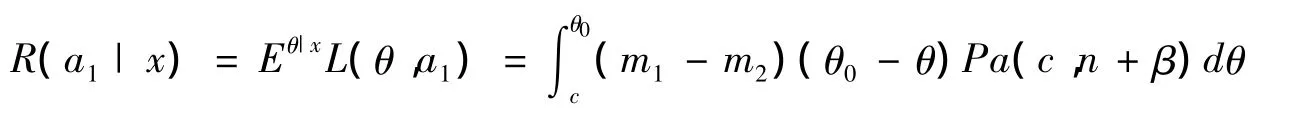
由式(1)及(3)，行动a2的后验风险为

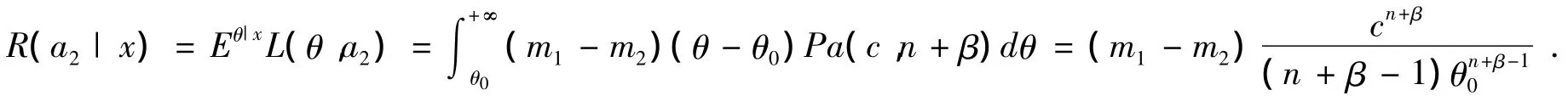
当θ0≤ c时，

同理，行动 a1的后验风险为 R(a1|x)=Eθ|xL(θ，a1)=0，

行动a2的后验风险为

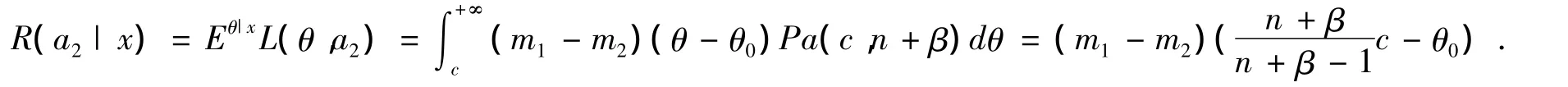
由于R(a1|x)＜R(a2|x)，故应当接受H0，认为θ＞θ0，行动a1更好.

对于决策者来说，如果认定总体X服从均匀分布，通过先验信息确定未知参数θ为帕累托分布，那么只要知道收益函数的平衡点θ0与c=max{α，x(n)}及n，β的值，就能得到相应的检验结果，从而采取相应的行动.而后验风险可以作为做决策的量化分析，通过其大小来衡量是否值得作出该决策，或者说，如果两个行动的后验风险相差不多时，考虑更加节约成本，获利更大的决策更佳.

3 实 例

某美术厂与外单位商谈一批美术品绘制任务.若绘制成功，每张美术作品可得800元;若绘制不成，每张要赔偿损失1 600元.为了决定是否接受该订单，厂长希望企划部门作出有理有据的决策，故进行如下调查.假设废品率X～U(0，θ).而根据该厂的技术力量估计θ～Pa(α，β).α=0.2，β=1.抽取过去10 年作品得到废品率分别为x1=0.1，x2=0.1，x3=0.05，x4=0.25，x5=0.04，x6=0.15，x7=0.13，x8=0.03，x9=0.04，x10=0.06.故 n=10，c=max{α，x10}=max{0.2，0.25}=0.25.设 H0:θ＞ θ0，H1:θ≤θ0.a1:接受H0，则不接单，a2:接受H1，则接单.每张美术作品收益函数为

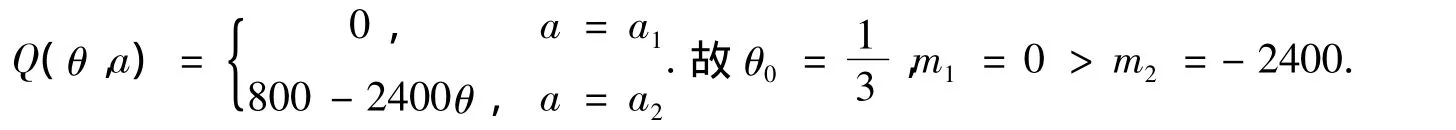
［1］张静.贝叶斯假设检验有经典假设检验的对比研究［J］.统计与决策，2012(9):36-37.

［2］贾旭山，金振中.二项分布贝叶斯假设检验方法［J］.现代防御技术，2008，36(5):37-40.

［3］姜培华，范国良.几种非正态总体参数的贝叶斯假设检验问题［J］.南通大学学报，2013，12(1):82-86.

［4］杨兴琼，张德然，周伟萍.一类非正态总体未知参数的Bayes假设检验［J］.绵阳师范学院学报，2007，26(8):14-16.

［5］茆诗松.贝叶斯统计［M］.北京:中国统计出版社，1999.