摇摆条件下矩形窄缝通道内汽泡脱离直径模型构建及分析

谢添舟，陈炳德，闫 晓，徐建军，黄彦平，肖泽军

(中国核动力研究设计院 中核核反应堆热工水力技术重点实验室，四川 成都 610041)

泡核沸腾传热由两部分构成：一是对流传热，二是汽泡生长及脱离。因此，汽泡脱离直径是沸腾传热机理模型研究中的重要参数之一。目前，汽泡脱离直径预测模型的研究方法之一是对单个汽泡在生长过程中的受力进行分析，通过受力平衡进行求解[1-4]。但现有模型均是在静止条件下获得的，而在摇摆条件下，由于瞬变外力场的引入，汽泡受力过程变得更加复杂。实验结果表明，摇摆条件下汽泡生长和脱离过程均会受到影响，进而影响通道内的传热过程。因此，开展运动条件下汽泡受力分析，探析摇摆运动条件下汽泡脱离机理，对运动条件下沸腾传热机理认知具有重要意义。

本工作在汽泡受力分析中引入摇摆运动所引起的瞬变外力场，构建摇摆条件下的汽泡脱离直径预测模型，通过实验数据进行验证，并对模型进行应用分析。

1 理论模型

1.1 静止条件下单汽泡受力分析

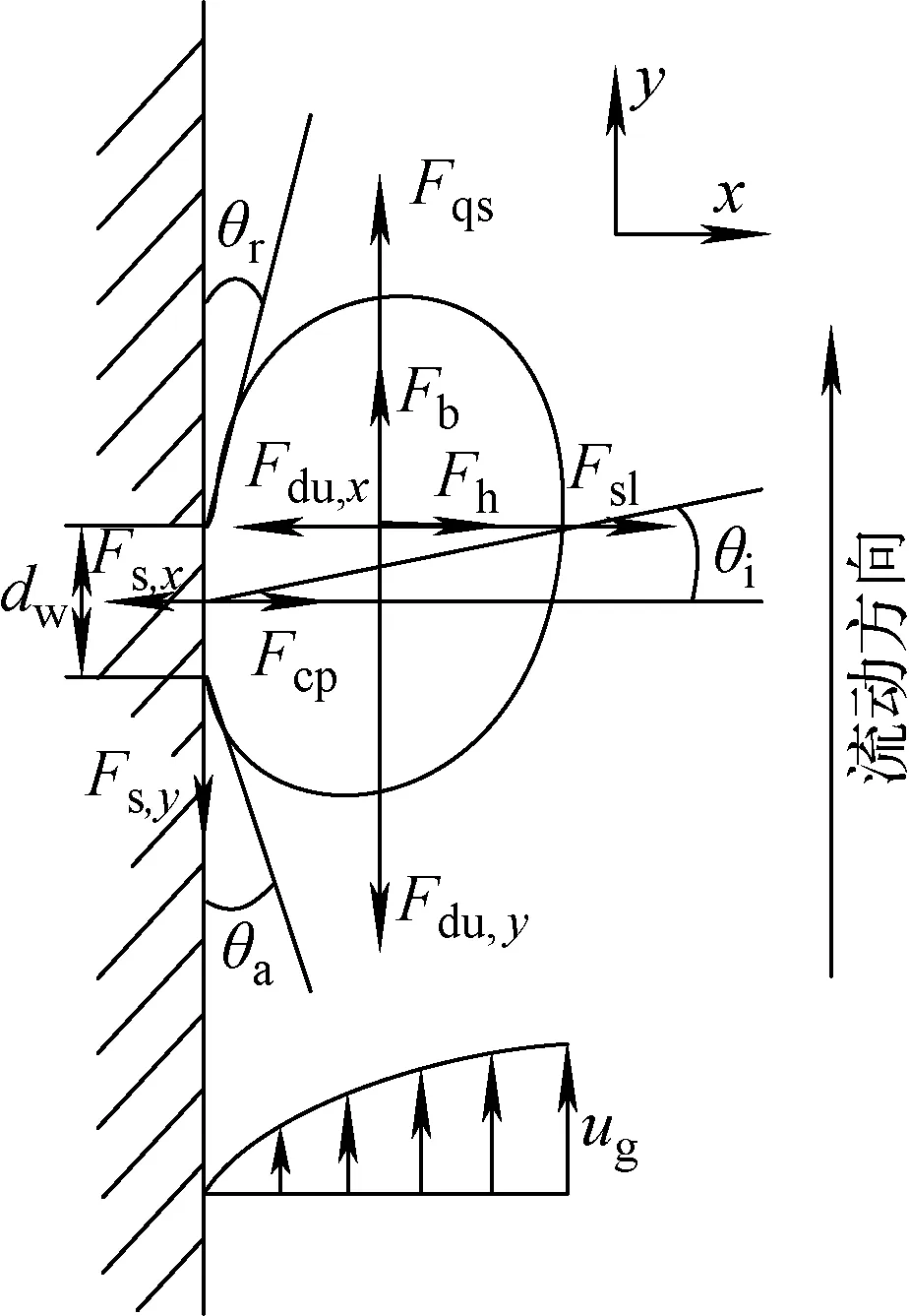
图1 汽泡受力示意图

根据Zeng和Thorncroft等[2-3]的研究结果，静止条件下汽泡受力示于图1。作用于汽泡上的力主要有：表面张力Fs、流动方向上准稳态曳力Fqs、由于汽泡的非对称生长形成的非稳态曳力Fdu、剪切力Fsl、浮力Fb、水压力Fh和接触压力Fcp。图1中，θi为汽泡受向上流体冲刷而产生的轴心倾斜角，θa和θr分别为汽泡的前后接触角，dw为汽泡与壁面的接触直径，ug为流体截面上的速度分布。由于汽泡在生长过程中紧贴壁面，因此在x和y方向上合力为0，即：

∑Fx=Fs,x+Fdu,x+Fsl+Fh+Fcp=0

(1)

∑Fy=Fs,y+Fdu,y+Fqs+Fb=0

(2)

1.2 摇摆运动产生的附加力

图2 典型摇摆运动条件下汽泡附加力示意图

根据实验中六自由度运动台产生的正弦摇摆运动，有：

θ(t)=θmsin(2πft)

(3)

(4)

(5)

式中：θ(t)为瞬时摇摆角位移；θm为摇摆振幅；ω为角速度；ε为角加速度；f为摇摆频率；t为时间。

当实验段做正弦运动时，汽泡除受到静止条件下的经典力作用外，还受到摇摆造成的向心力、切向力和科氏力作用，由于汽泡脱离前紧贴壁面，与实验段无相对运动，因此汽泡受到的科氏力为零。向心力和切向力的表达式如下：

πρbω2r′

(6)

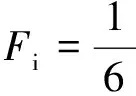
(7)

式中：Db为汽泡直径；ρb为汽泡密度。

将向心力和切向力分解，有：

(8)

(9)

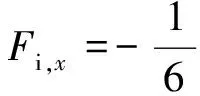
(10)

(11)

1.3 摇摆角位移的影响

摇摆运动时，除运动产生的附加力外，汽泡浮力在x和y方向上的分量也会随摇摆角位移发生变化，有：

Fb,x=Fbsinθ(t)

(12)

Fb,y=Fbcosθ(t)

(13)

1.4 摇摆条件下汽泡受力模型

将向心力、切向力及改变后的浮力代入式(1)和(2)，有：

∑Fx=Fs,x+Fdu,x+Fsl+Fh+

Fcp+Fb,x+Fn,x+Fi,x=0

(14)

∑Fy=Fs,y+Fdu,y+Fqs+

Fb,y+Fn,y+Fi,y=0

(15)

汽泡保持在核化点时，应满足两个准则：1) ∑Fx<0； 2) ∑Fy<0。当两个准则中任何一个被破坏时，汽泡脱离核化点，此时汽泡的直径为脱离直径。

2 模型验证

可视化实验在中国核动力研究设计院六自由度运动台上进行，实验工况为质量流速G=300和700 kg/(m2·s)，入口过冷度Δtsub为40 ℃，压力p为0.15 MPa，摇摆振幅θm为10°～30°，频率f为0.1～0.32 Hz。前期实验测定θi为5°，θa和θr分别为42°和40°，dw约为汽泡直径的0.45倍。实验中加热段起始点与核化点之间的距离zd=0.175 m时，r′=0.74 m，θ′=7.8°；zd=0.2 m时，r′=0.76 m，θ′=7.5°。通过实验共获取数据点54个，汽泡脱离直径模型预测值和实验测量结果的对比示于图3。图3中，汽泡脱离直径约为0.14 mm和0.07 mm的数据分别对应的质量流速G为300和700 kg/(m2·s)。从图3可看出，预测值与实验值的相对偏差在±15%以内，二者符合较好。

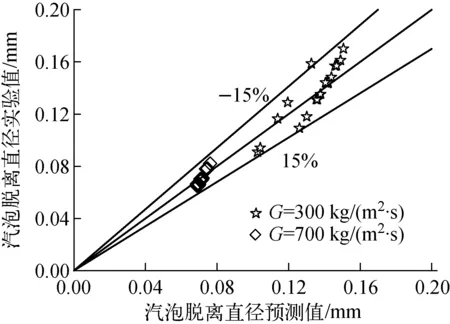
图3 摇摆运动条件下汽泡脱离直径预测值和实验值比较

3 模型分析

3.1 模型中的受力分析

实验中各力的范围列于表1。通过分析汽泡脱离时的受力发现，均是y轴方向上合力大于零，而x轴方向上合力小于零，表明汽泡脱离核化点后沿流动方向滑移，这与实验观察到的现象一致。计算中发现，摇摆运动时y方向上向心力Fn，y和切向力Fi，y的量级在10-15～10-14之间，而浮力、表面张力和稳态曳力等的量级为10-9～10-8，表明汽泡本身所受附加力很小，对汽泡脱离直径的影响可忽略不计，但由于浮力、表面张力和稳态曳力的量级基本一致，因此，摇摆运动导致的浮力改变对汽泡脱离直径的影响必须加以考虑。

表1 摇摆运动时各力的范围

3.2 摇摆振幅对汽泡脱离直径的影响

由受力分析可知，摇摆频率只影响汽泡所受向心力和切向力，而瞬时的角位移会影响浮力在y轴方向的分量，因此有必要研究摇摆振幅对汽泡脱离直径的影响。当实验段处于摇摆运动时，由于汽泡有可能在运动周期中任意时刻脱离，因此其脱离直径会在一定范围内波动。在模型中固定质量流速，将角位移设定为0°和±θm，再改变摇摆振幅重新计算，结果示于图4。从图4可看出，不同质量流速下，均是角位移θ=0°时汽泡脱离直径最小，θ=±θm时汽泡脱离直径最大。

同时，随着摇摆振幅的增加，汽泡脱离直径有可能存在的范围增大，即汽泡脱离直径可能在更大范围内波动，而质量流速的增大会抑制这种效应，该趋势和实验结果一致，但计算得到的波动幅值较实验值小，这可能是由于模型中未考虑摇摆运动引起的局部流场波动以及汽泡脱离本身具有的随机性[1]。

3.3 不同产生时刻对汽泡脱离直径的影响

低质量流速下摇摆振幅对汽泡脱离直径的影响较大，因此，对G=300 kg/(m2·s)时同一周期内汽泡在不同时刻生长对其脱离直径的影响进行深入分析。假定从t=0时刻开始，每间隔1 s产生1个汽泡，在模型中分别计算其脱离直径。计算中设定摇摆振幅为30°和60°，频率为0.1 Hz，计算结果示于图5。图5中，正弦曲线为摇摆运动角位移曲线，各点对应的曲线为不同时刻产生汽泡的生长曲线，生长曲线中最后1个点为汽泡脱离点，此时的汽泡直径为汽泡脱离直径。从图5可看出，在同一摇摆运动周期内，角位移趋于0°时，汽泡脱离直径趋于最小，而角位移趋于±θm时，汽泡脱离直径趋于最大；摇摆振幅越大，该趋势越明显(图5b)。这是因为角位移为0°时，实验段处于中心位置，此时汽泡所受浮力在流动方向上分量最大，汽泡更易脱离；而当角位移由0°变大或变小时，汽泡所受浮力在流动方向上的分量均变小，因此汽泡脱离直径变大。

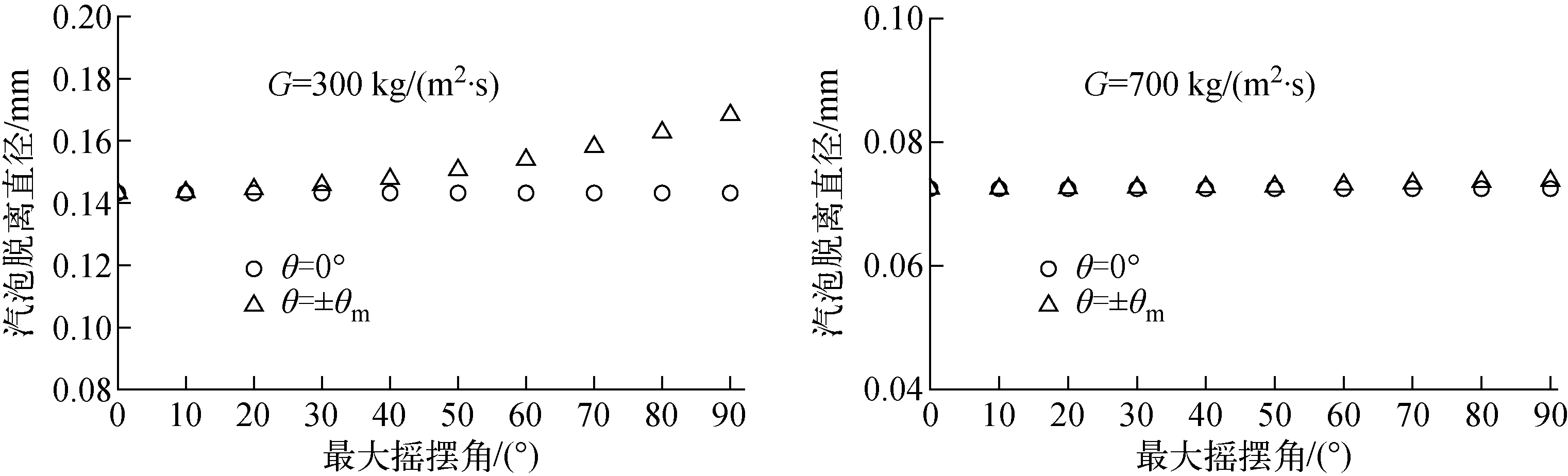
图4 摇摆振幅与汽泡脱离直径的关系

p=0.15 MPa，Δtsub=40 ℃，G=300 kg/(m2·s)，f=0.1 Hz

3.4 流量波动对汽泡脱离直径的影响

文献[5]指出，当回路驱动压力较小时，摇摆运动会导致与摇摆周期相同的系统流量波动，本工作通过模型研究了质量流速为300和700 kg/(m2·s)时可能产生的系统流量波动对汽泡脱离直径的影响。由于流量为周期性变化，且摇摆运动和流量波动传递滞后时间的影响因素复杂，很难将流量波动直接引入模型，因此在计算中将流量固定为最大值和最小值，即可知道该流量波动条件下汽泡脱离直径可能的波动范围。模型计算结果示于图6。由图6可看出，不同质量流速下，同等程度的流量波动引起的汽泡脱离直径波动基本相同，且当流量波动达到5%时，汽泡脱离直径波动接近10%。这表明如果系统存在5%以上的流量波动，其对汽泡脱离直径的影响必须加以考虑。

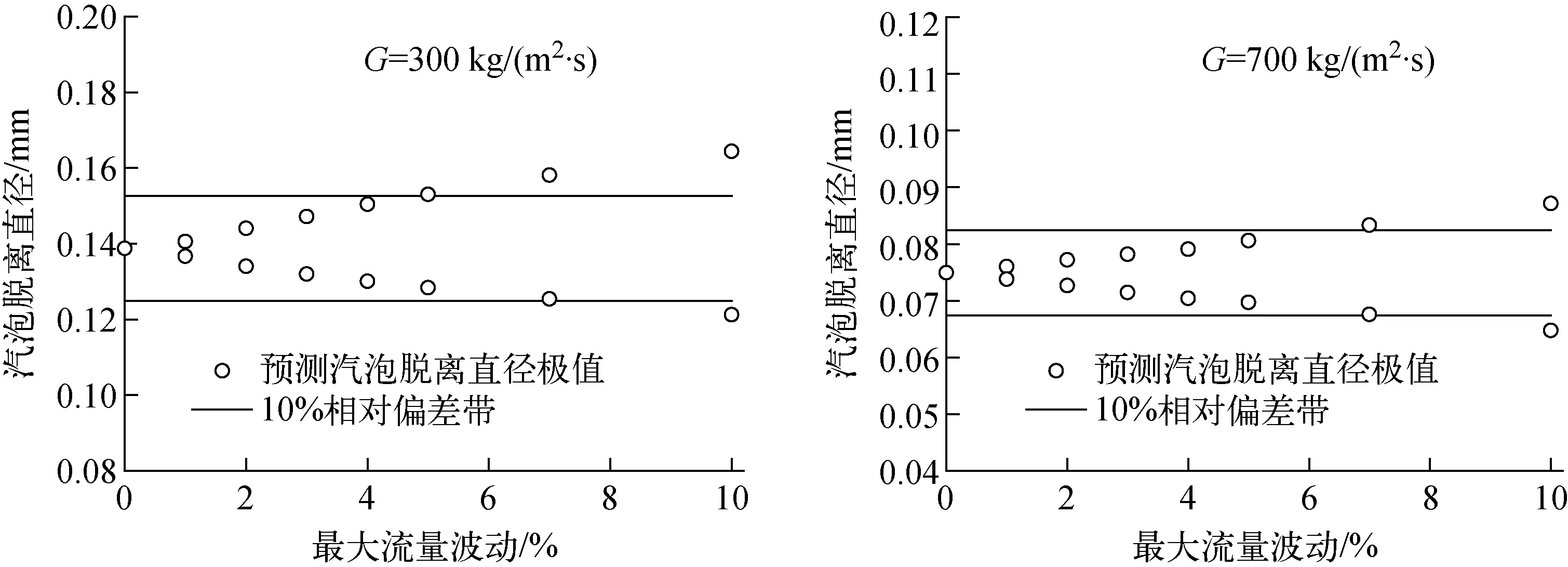
图6 流量波动对汽泡脱离直径的影响

4 结论

本工作对摇摆运动条件下矩形窄缝通道内过冷沸腾时单汽泡进行了受力分析，建立了摇摆条件下汽泡脱离直径预测模型，并通过实验进行验证，与实验结果吻合良好。同时进行了受力分析，发现在汽泡脱离过程中浮力、稳态曳力和表面张力起主要作用，摇摆运动引起的浮力波动必须加以考虑。模型计算发现角位移为0°时，汽泡脱离直径最小。如果系统存在5%以上的流量波动，则其对汽泡脱离直径的影响必须加以考虑。

参考文献：

[1] KLAUSNER J F, MEI R, BERNHAND D M, et al. Vapor bubble departure in forced convection boiling[J]. Int J Heat Mass Transfer, 1993, 36(3): 651-662.

[2] ZENG L Z, KLAUSNER J F, BERNHAND D M, et al. A unified model for the prediction of bubble detachment diameters in boiling systems, Ⅱ: Flow boiling[J]. Int J Heat Mass Transfer, 1993, 39: 2 271-2 279.

[3] THORNCROFT G E, KLAUSNER J F, MEI R. Bubble force and detachment models[J]. Multiphase Science and Technology, 2001, 13: 35-76.

[4] SITU R, HIBIKI T, ISHII M, et al. Bubble lift-off size in forced convective subcooled boiling flow[J]. Int J Heat Mass Transfer, 2005, 48: 5 536-5 548.

[5] 谭思超，张红岩，庞凤阁，等. 摇摆运动下单相自然循环流动特点[J]. 核动力工程，2005，26(6)：554-558.

TAN Sichao, ZHANG Hongyan, PANG Fengge, et al. Characteristics of single-phase natural circulation under rolling[J]. Nucl Power Eng, 2005, 26(6): 554-558(in Chinese).