铀生产工艺设备中滞留量测量的自吸收校正方法
2014-08-07何丽霞隋洪志陈立君
何丽霞,甘 霖,*,隋洪志,陈立君
(1.中国原子能科学研究院 放射化学研究所,北京 102413;2.中国核工业集团公司,北京 100086)
铀燃料循环生产工艺过程中的某些环节有部分物料的残渣和溶解液沉积,溶解阶段形成的滞留量成为影响铀生产衡算的重要因素,为实现铀生产线核材料的闭合衡算,必须对滞留量进行准确测量。测量存在较大难度,容器的几何结构、其所处的空间条件、滞留量的介质成分等均会对测量结果产生影响,而其中最大的困难在于物料的自吸收影响校正。Reilly等[1]对可回收样品测量的自吸收修正、自吸收校正技术和存在的问题给出了理论分析。国内也有针对特定对象的自吸收校正方法研究[2-3],主要通过数学方法和蒙特卡罗模拟技术解决。本文拟在物料厚度、介质成分、几何参数不确定的条件下,初步建立自吸收二维校正模型。
1 自吸收影响
若某放射性物料分布为理想面源,其自发射的γ射线在远场一阶近似条件下,自吸收的表达式[3]为:
μiRS≫1
(1)
式中:Gi为第i条γ射线放射性物料的自吸收因子;RS、t为放射性物料的几何参数;μi为特定能量γ射线的线性衰减系数;i为某同位素不同能量的特征γ射线,i=1,2,3,4对应的235U的特征γ射线能量分别为143、163、186和205 keV。
而在某些铀生产工艺设备中,铀的滞留量几何分布不规则,可能是酸性溶液、粘稠物或干燥物等。此时,γ射线在其中的自吸收规律与式(1)不同,类似指数衰减分布,但Gi均可表示为:
(2)
式中:Ii为实际测量条件下某γ射线的计数率;I0为无自吸收时该γ射线的计数率。
2 自吸收修正过程
鉴于铀生产工艺设备中滞留量不确定性强的特点,量化分析数据需归一化处理,物料含量使用质量厚度,单位取g·cm-2。设自吸收因子与质量厚度之间的关系为:
(3)
式中:Tj为物料的质量厚度;Gij为质量厚度j条件下第i条γ射线的自吸收因子;aij、bij、ci为待定系数,通过系统刻度得到。
将式(3)定义为某特征γ射线的自吸收纵向变化曲线,即其自吸收因子随质量厚度的变化关系。同一放射性同位素发射的特征γ射线分支比固定并已知[4],在某质量厚度条件下,自吸收因子随能量的变化为:
Gji=ajiEi+bji
(4)
其中,Ei为γ射线的能量。该式定义为某质量厚度下,γ射线的自吸收横向变化曲线。
因特征γ射线的相关性,两条曲线必然存在交点,即物理意义上的自吸收因子,此时,Gij=Gji,而aij≠aji,bij≠bji。不同能量γ射线的自吸收效应不同,能量越低,自吸收越显著[5]。
2.1 确定无自吸收时的探测效率
无自吸收时,首先,需保证源与探测器的距离足够大,测量对象近似为点源,可使源的径向分布对测量结果的影响最小化;其次,物料分布应足够薄,轴向近似无自吸收。
取已知活度的含235U的物料进行系统校准,按无自吸收的条件装入容器,测定该测量条件下235U 4条特征γ射线的探测效率,探测效率εi[6]为:
(5)
式中:εi为特征γ射线的探测效率;Ci为特征γ射线的能峰总计数;A为被测物料中235U的比活度,Bq·g-1;Bi为特征γ射线的分支比;t为测量时间,s;W为235U的质量,g;Ω为测量几何条件。无自吸收时,Gij=1。
2.2 建立自吸收模型
系统校准时,选取的物料厚度各不相同,特征量值分布具有一定的梯度范围。首先不考虑自吸收的影响,利用测量所得的特征γ射线计数率推算235U活度,此值与活度真值相比即得该特征γ射线的自吸收因子。因此,系统校准的结果是,得到多种质量厚度条件下不同能量特征γ射线的自吸收因子矩阵。
另外,在某质量厚度条件下,不同能量γ射线的自吸收因子与主要γ射线的自吸收因子相比,可得到一组自吸收因子比,因此系统校准的自吸收因子矩阵也可用自吸收因子比矩阵表示。235U分析取186 keV γ射线为主要γ射线。
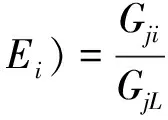
(6)
式中:Sji(Tj,Ei)为特征γ射线的一组自吸收因子比;GjL为主要γ射线的自吸收因子。
2.3 分析时引入自吸收校正
不同质量厚度的物料,其特征γ射线的自吸收独具特点,反应在其自吸收因子比上,则是一组具有唯一性的数值,与系统校准结果之间存在差异。
假定未知物料质量厚度为Tm,测量获取特征γ射线计数率,再利用系统校准时得出的探测效率推算自吸收因子比,即Smi(Tm,Ei)。然后,将这组自吸收因子比与系统校准的矩阵进行比较,可选择合适的边界条件,用拉格朗日线性插值方法[7]计算该物料的各非主要γ射线的自吸收因子Gmi,有:
当Smi(Tm,Ei)
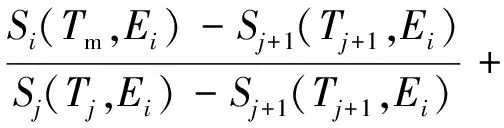
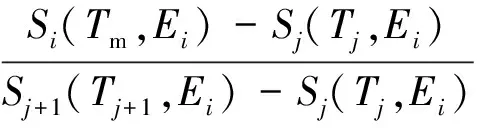
(7)
Gji、Gj+1,i、S等均通过系统刻度得到,由此,可推算主要γ射线的自吸收因子GmL:
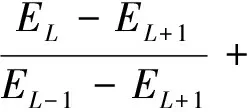
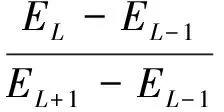
(8)
3 系统校准
在实验室条件下开展滞留量的模拟测量,用已有条件构建适用于铀生产工艺设备的测量模型,建立自吸收修正关系。
3.1 实验条件
测量系统为HPGe探测器和多道谱仪,物料为天然U3O8粉末,容器为圆柱形,其内径为70 mm,装料时铺平、压实。测量时,探测器位于物料轴向,距离大于25 cm。各实验参数列于表1。
3.2 无自吸收时的探测效率
无自吸收的测量条件同3.1节所述,物料填充厚度为1 mm,相应的质量厚度为0.22 g·cm-2,测量后可根据式(5)计算得到235U各特征γ射线的探测效率,结果列于表2。
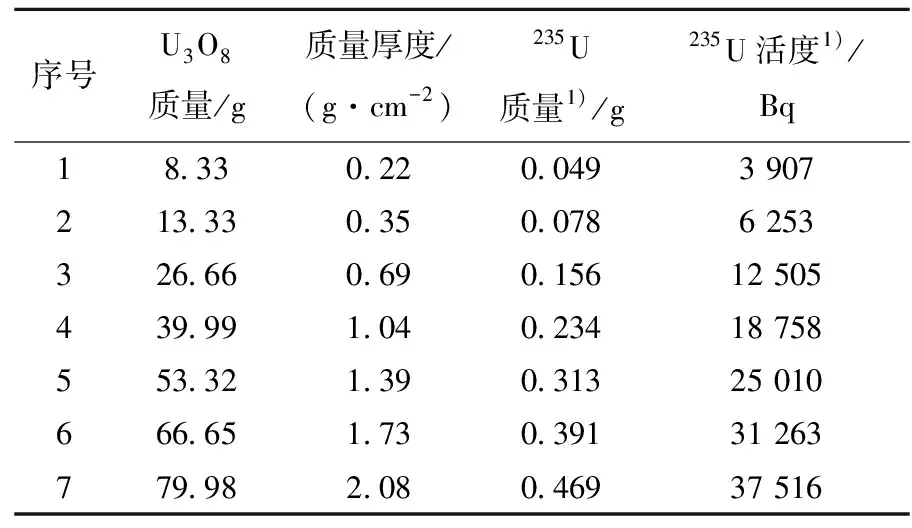
表1 用于系统刻度的U3O8的参数

表2 235U各特征γ射线的探测效率
3.3 自吸收因子比矩阵计算
1) 推算235U比活度
将系统校准所用到的各质量厚度条件下测量得到的235U特征γ射线的计数率推算成235U比活度,结果列于表3。
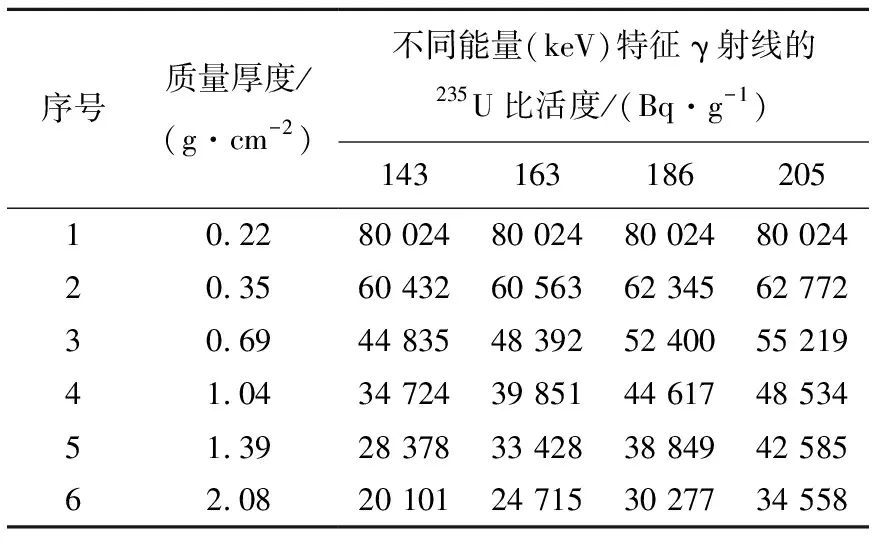
表3 不同质量厚度的235U比活度
从表3可看出,不同质量厚度条件下,由235U特征γ射线的计数率推算所得的235U比活度,随质量厚度的增加而减小,程度与γ射线能量亦相关。
2) 构建自吸收因子矩阵
以无自吸收条件下的235U比活度作为特定标准,将表3进行转换,即得系统校准的自吸收因子矩阵,数据列于表4。
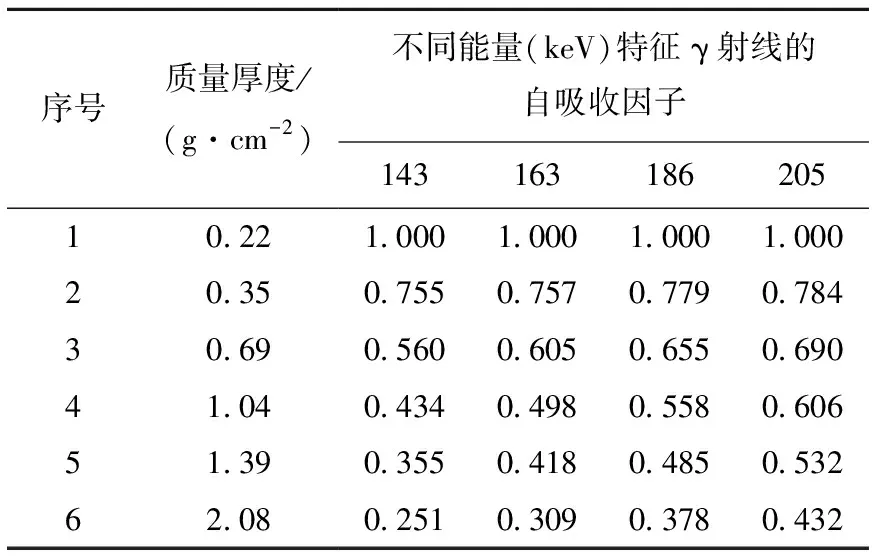
表4 自吸收因子矩阵
依据自吸收因子矩阵,分别取质量厚度和特征γ射线的能量为变量,可拟合得到自吸收纵向变化曲线和横向变化曲线的系数,本系统校准的纵向变化曲线拟合参数列于表5。
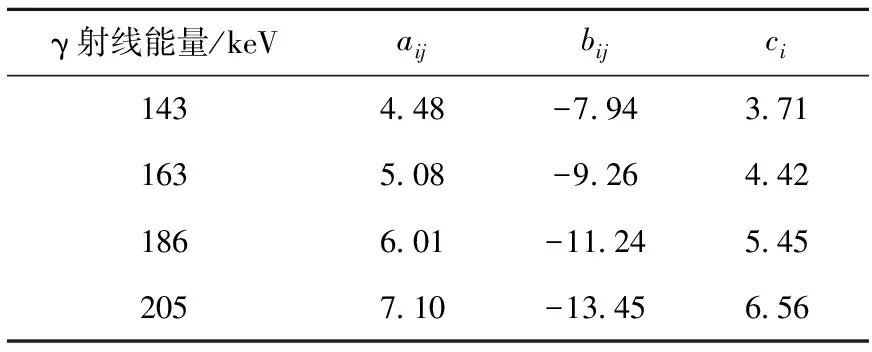
表5 235U自吸收纵向变化曲线拟合参数
4 实验验证
取2个样品进行自吸收校正方法验证,样品A质量厚度为1.73 g·cm-2,样品B接近于饱和厚度,测量条件与系统校准过程保持一致(探测效率见表2),首先不考虑自吸收影响,应用式(9)计算235U的活度,其中,Gij暂取1,结果列于表6。
(9)
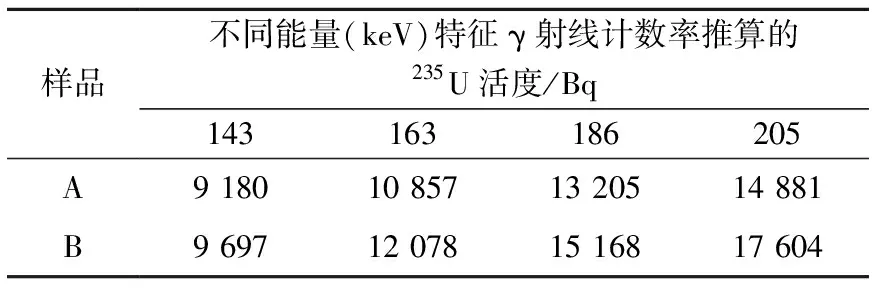
表6 依特征γ射线计数率推算的235U活度
因质量厚度确定的条件下,235U的活度真值必定唯一,将各推算活度与主要γ射线的推算活度相比,即分别得到两个验证样品的一组自吸收因子比,结果列于表7。
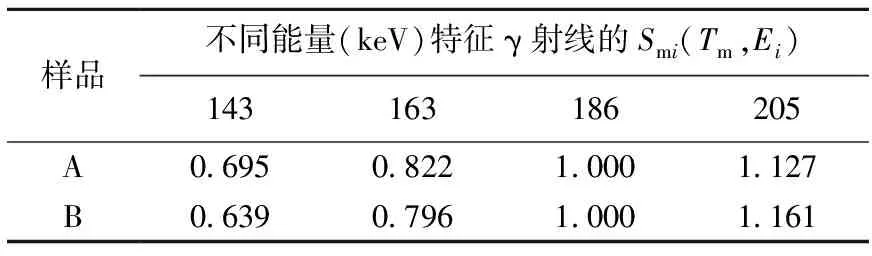
表7 待测样品的自吸收因子比
将计算结果与系统校准的自吸收因子矩阵对比可得出:样品A的质量厚度介于1.39 g·cm-2和2.08 g·cm-2之间。故选择这两个质量厚度的自吸收因子,代入式(7)进行插值计算,得出该条件下235U各特征γ射线的自吸收因子:Gm,1=0.289,Gm,2=0.356,Gm,4=0.476。通过式(8)计算186 keV的自吸收因子Gm,3=0.425;用同样方法计算样品B各特征γ射线的自吸收因子。
此时待解未知量为质量厚度,已知235U各条特征γ射线的自吸收因子,选用纵向变化曲线拟合参数(表5)计算待测物料的质量厚度,结果列于表8。

表8 待测样品的自吸收因子及质量厚度
5 结语
针对铀生产工艺设备内滞留量的特点,开展了物料自吸收校正方法的研究,利用某核素多条特征γ射线在物料中自吸收程度不同的特点,通过系统校准,构建了235U特征γ射线自吸收因子矩阵,与射线的能量和不同质量厚度的关系呈现二维特点,因此称之为自吸收二维修正模型。优点在于避免了常规方法的不确定性,数据处理分析过程简单可行。
实验证明,当待测物料的质量厚度未达到各特征γ射线的饱和吸收厚度时,采用此模型推算得到的物料质量厚度相对偏差较小;而当待测物料达到射线的饱和厚度时,计算结果存在较大偏差。另外,若物料的质量厚度非常小,由于各能量γ射线的自吸收不显著,此条件下进行自吸收效应分析也会带来较大偏差。
参考文献:
[1] REILLY D, ENSSLIN N, SMITH H, Jr, et al. Passive nondestructive assay of nuclear materials, NUREG/CR-5550[R]. US: Nuclear Regulatory Commission, 1991.
[2] 陆向东,谢东,田东风. 任意几何形状源的γ射线自吸收修正[J]. 核技术,2003,26(10):759-762.
LU Xiangdong, XIE Dong, TIAN Dongfeng. The γ-ray self-absorption correction for sources with random geometrical shape[J]. Nuclear Techniques, 2003, 26(10): 759-762(in Chinese).
[3] 陆向东,田东风,谢东. 双层介质核材料的γ特征谱分析[J]. 核技术,2004,27(11):814-817.
LU Xiangdong, TIAN Dongfeng, XIE Dong. The γ spectra analysis for two-layer nuclear material[J]. Nuclear Techniques, 2004, 27(11): 814-817(in Chinese).
[4] 卢希庭. 原子核物理[M]. 北京:原子能出版社,2001:103.
[5] 复旦大学,清华大学,北京大学. 原子核物理实验方法[M]. 北京:原子能出版社,1997:65.
[6] THOMAS E S, THOMAS A K. PC/FRAM user manual, LA-UR-99-998[R]. US: LANL, 2001.
[7] 李庆扬,王能超,易大义. 数值分析[M]. 北京:清华大学出版社,2003:23.
