一类二维动力系统的稳定性及分叉分析
2014-08-06胡军浩
胡军浩,晏 磊
(中南民族大学 数学与统计学学院,武汉 430074)
映射动力系统具有比常微分方程系统更复杂的动力学性质,例如,一维Logistics映射就可产生混沌现象,而三维自治常微分系统才能产生混沌[1,2]. 在经济学和生物学中,许多数学模型可以用可化为叠映射的动力系统来表示,而其中一大类模型均可利用具有参数零化的不完整结构形式的二阶二次差分方程来描述[2-5]. 文献[2]基于一定的假设对二阶二次差分方程进行简化,应用二维连续不可逆映射系统的关键集理论重点探讨一类二阶二次差分方程的全局动力学性质. 本文将在文献[2]的基础上,运用动力学理论,重点探讨一类二维动力系统的局部稳定性与分叉性质,揭示系统的局部动力学行为,为系统在特定参数取值下混沌行为存在性的证明打下基础.
1 模型重述
考虑如下二阶二次差分方程
当a00=0,a01≠0,a10≠0,a02≠0,a20≠0,x=xn,y=xn-1时,可以将其简化为:
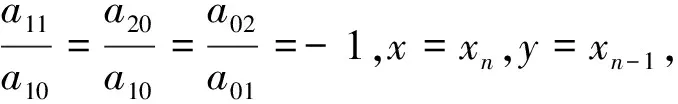
2 不动点的稳定性与分叉
考虑文献[2]中提出的二维动力系统模型:
(1)
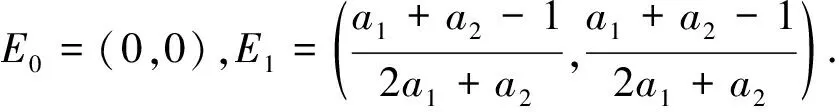
系统(1)的Jacobian矩阵
J(x,y)=
(2)
特征多项式为:
f(λ)=λ2+(2a1x+a1y-a1)λ+
(a1x+2a2y-a2).
(3)
根据Jury条件和二维系统分叉定理[6],关于系统(1)的2个不动点的局部稳定性,有如下定理1.
定理1 (E0的局部稳定性)
(1)当a2>-1且a1<|1-a2|时,系统(1)在不动点E0=(0,0)处渐近稳定;
(2)当a1=1-a2时,系统在E0处产生Fold分叉;
(3)当a1=a2-1时,系统在E0处产生Flip分叉;
(4)当a2=-1且-2 证明系统(1)在边界平衡点E0=(0,0)处的Jacobian矩阵 (4) 对应的特征多项式f(λ)=λ2-a1λ-a2. 根据Jury条件[6]: 当参数取值使得f(1)=1-a1-a2>0,f(-1)=1+a1-a2>0,1-f(0)=1+a2>0时,平衡点E0稳定,即有定理1中的(1); 当f(1)=1-a1-a2=0时,系统在E0处产生Fold分叉,即有定理1中的(2); 当f(-1)=1+a1-a2=0时,系统在E0处产生Flip分叉,即有定理1中的(3); 定理2(E1的局部稳定性) (2)当a1+a2=1时,系统在E1处产生Fold分叉; 证明证明过程同定理1,故省略. 首先验证不动点E0的稳定性和分叉. 固定参数a2=0.5,根据定理1的结论,系统(1)在a1=-0.5时发生Flip分叉,在a1=0.5时发生Fold分叉,在a1∈(-0.5,0.5)时渐近稳定. 如图1(a)所示,当-0.5 固定参数a2=-1,根据定理1的结论,当-2 图1 系统(1)的变量x关于参数a1的分叉图(因为y′=x,所以图1仅显示变量x的分叉图,下同)Fig.1 The bifurcation diagrams of the variable x in the system (1) with respect to the parameter a1(since y′=x, so the Fig.1 only show the bifurcation diagrams of the variable x,and the same below) 需要说明的是,由定理2可知,当a1=-2.5时系统在不动点E1处产生Flip分叉,而当a1=-0.89时,系统已经在E1处由于Neimark-Sacker分叉产生周期波动,因此在该参数取值下不会产生Flip分叉. 图2 系统(1)的变量x关于参数a1的分叉图Fig.2 The bifurcation diagrams of the variable x in the system (1) with respect to the parameter a1 从定理1可以知道当a1=a2-1时,系统在E0处产生Flip分叉;这一部分我们将利用中心流形定理[7]来研究在不动点E0=(0,0)处的稳定性. 当a1=a2-1时,在原点(0,0)处可以将系统(1)写为: (5) (6) 通过中心流形定理可知,系统(6)存在一个中心流形,表示为: Wc(0)={(u,v)∈R2|v=h(u),h(0)=h′(0)=0,|u|<δ}. (7) 其中δ是一个足够小的正常数. 令v=h(u)=b1u2+b2u3+O(u4),则有: h(-u+f(u,h(u)))2-a2h(u)-g(u,h(u))=0. (8) (9) 那么系统(5)在中心流形上由映射 (10) 限制,而f1的Schwarzian导数为: (11) 定理3 当系统(1)的参数满足a1=a2-1,关于不动点E0=(0,0)的稳定性有: (3)当a2∈(1,+∞)时,系统(1)的不动点E0是一个不稳定结点. 利用坐标变换: 将系统(1)的正不动点E1转移到原点(0,0),得到: (12) (13) (14) (14)式中f(N,Q)=g(N,Q)=AN2-BQ2-CNQ,且 通过中心流形定理可知,系统(6)存在一个中心流形,表示为: Wc={(N,Q)∈R2|Q=h(N),h(0)=h′(0)=0,|N|<δ}, (15) 其中δ是一个足够小的正常数. 令Q=h(N)=c1N2+c2N3+O(N4),则有: (16) (17) 那么(5)式在中心流形上由映射 f1:N|→-N+f(N,h(N))=-N+AN2- (18) 限制,而f1的Schwarzian导数为: (19) 本文考虑了一类二阶二次差分方程经过简化后得到的二维动力系统,应用非线性动力学的相关理论,研究了该系统不动点的稳定性与分叉情况,并利用中心流形定理就不动点在Flip分叉时的稳定性进行了探讨,揭示了该系统复杂的动力学现象. 众所周知,Flip分叉(倍周期分叉)是一条通向混沌的典型道路[8],在一定的Flip分叉参数取值下,系统(1)的分叉图产生的混乱(如图1(b))是真的混沌还是准周期行为,限于篇幅本文没有进行深入讨论,拓扑马蹄理论则是证明混沌的强有力的工具[9,10],在后续研究中,我们将利用该理论证明系统(1)的混沌性并对混沌进行控制. 参 考 文 献 [1] Hirsch M W,Smale S,Devaney R L.Differential equations,dynamical system,and an introduction to chaos [M].Amsterdam: Elsevier,2005: 244-245. [2] 顾恩国,王杰群,程 丽.一类二次二阶差分方程的动力学分析[J].武汉理工大学学报:交通科学与工程版,2011,35(2): 421-424. [3] Foroni I,Gardini L.Homoclinic bifurcation in hetero-geneous market models [J].Chaos,Solitions and Fractals,2003(15): 743-760. [4] Gu E G.The feasible domains and their bifurcations in an extended Logistic model with an external interference [J].International Journal of Bifurcation and Chaos,2007(3): 877-889. [5] Gu E G,Huang Y B.Global bifurcation of domains of feasible trajectories: analysis of a predator prey model [J].International Journal of Bifurcation and Chaos,2006(9): 2601-2613. [6] Saber N E.Discrete chaos[M].New York:Chapman Hallcrc,2000:165. [7] Wiggins S.Introduction to applied nonlinear dynamical systems and chaos[M].New York: Springer,2000:257-262. [8] 顾恩国,李晓东,向 蕾,等.带有保护区的单一渔业资源的离散动力学模型分析[J].中南民族大学学报:自然科学版,2013,32(1):97-101. [9] Yang X S.Topological horseshoes and computer assisted verification of chaotic dynamics[J].International Journal of Bifurcation and Chaos,2009(4): 1127-1145. [10] Li Q,Yang X S.A simple way for finding topological horseshoes[J].International Journal of Bifurcation and Chaos,2010(4): 467-478.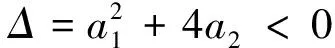

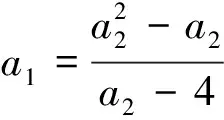

3 数值模拟



4 不动点在Flip分叉的临界稳定性
4.1 不动点E0在Flip分叉的稳定性
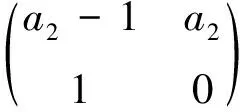
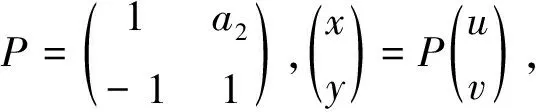
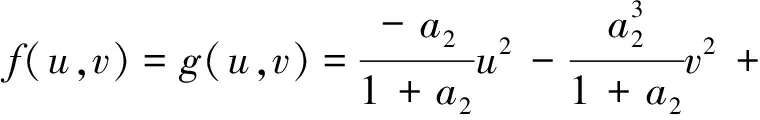

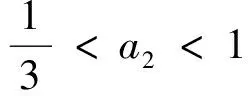


4.2 不动点E1在Flip分叉的稳定性



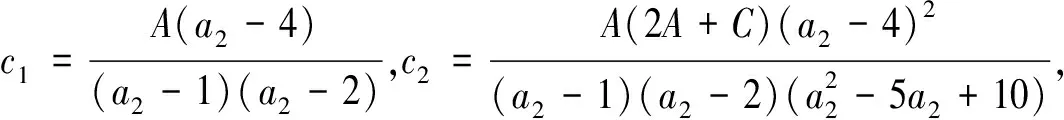
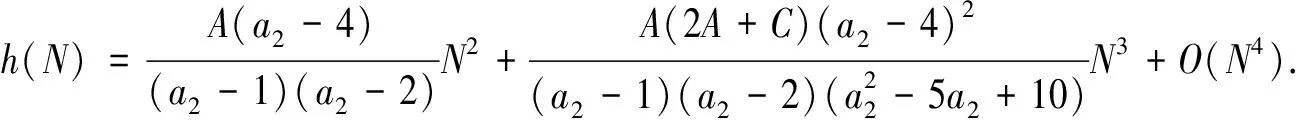
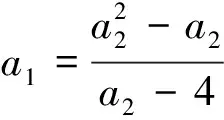



5 结语
