用SAS软件实现高维列联表资料的统计学分析：因变量为二值变量的多重logistic回归分析

胡良平，沈 宁，柳伟伟

(军事医学科学院研究生部生物医学统计学咨询中心，北京 100850)

1 方法原理

Logistic回归分析属于概率型回归分析，其应用范围很广，不仅适用于流行病学中病因学的分析，也可用于临床疗效评价和卫生服务研究等。它适用于因变量是定性变量的案例，包括二值变量、多值有序变量和多值名义变量。Logistic回归分析对自变量的数目有一定要求，一般来说，要求样本含量为自变量个数的10倍以上，结果稳定性好；对自变量的性质没有特殊要求，自变量可以是连续性变量、二值变量、多值有序变量或多值名义变量。

程序编写中，用Y代表因变量，其取值为0和1，分别表示发生阳性与阴性结果，X1、X2、…、Xm分别代表m个自变量。设P(Y=1|X1,X2,…,Xm)表示在自变量X1、X2、…、Xm存在的条件下出现阳性结果的概率，简记为P，则多重logistic回归分析模型可以表示为：

式中β0为常数项，β1、β2、…、βm分别为各个自变量所对应的回归系数。阳性结果发生的概率为P，则阴性结果发生的概率为(1-P)。P与(1-P)之比值被叫做优势比(OR)。对OR取自然对数，称为对P作logit变换，用logitP来表示。

由此logistic模型又可以表示为如下的形式：

logitP=β0+β1X1+β2X2+…+βmXm

注意，概率P与自变量X1、X2、…、Xm之间的关系是非线性的，但是logitP和自变量之间呈线性关系。Logistic回归分析模型中各参数都有明确的实际意义，回归系数βi表示在其他影响因素不变的情况下，自变量Xi每变化一个单位时所引起的logitP的改变量，Xi对应的ORi=expβi。当某种疾病的发病率或病死率很低时，可以用OR近似地估计相对风险度(relative risk,RR)。

从整体上理解logistic回归分析，可以根据操作过程依次总结为以下几个方面：自变量筛选，建立回归模型，以及检验部分(包括回归系数的检验、整体模型检验以及模型拟合优度检验)。(1)自变量筛选：筛选自变量的方法主要有前进法、后退法、逐步法和最优子集法。与多重线性回归不同的是，logistic回归分析筛选自变量时所用的检验不是F检验，而是似然比检验、计分检验和Wald检验。(2)检验部分：在logistic回归分析中，参数的估计通常采用最大似然法。在估计出回归系数后，对全部回归系数是否均为0做出的检验和对单个回归系数的检验，常用的检验方法有似然比检验、计分检验和Wald检验。(3)模型拟合优度检验：在建立回归方程后需要对模型做出评价，考察模型与实际数据的符合情况，称为拟合优度检验。在logistic回归分析中，用于拟合优度评价的统计量主要包括Pearson χ2值、偏差、Hosmer-Lemeshow统计量和一些信息测量指标。信息测量指标包括Akaike信息准则(AIC)和贝叶斯信息准则(BIC)。这两个指标在其他众多模型的评价中都可以看到，其取值越小，表明模型拟合越好。

2 实 例

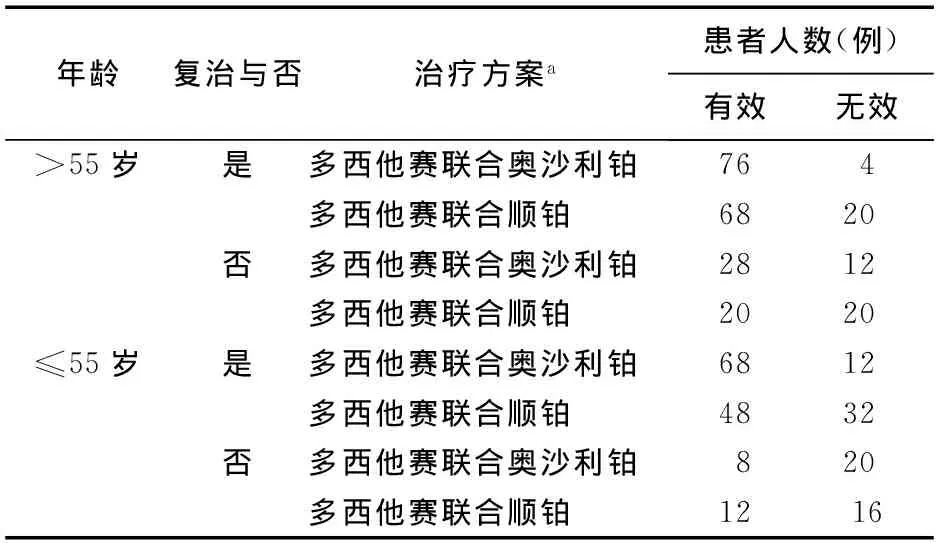
以晚期非小细胞肺癌患者作为研究对象进行的回顾性研究中， 分析多西他赛联合奥沙利铂与多西他赛联合顺铂的疗效差异是否具有统计学意义。 评价指标为接受不同方案治疗有效的患者数， 疾病完全缓解、 部分缓解和稳定被定义为有效， 疾病进展和死亡定义为无效。 在考察过程中， 研究者发现对疗效可能有影响的因素除药物外， 还有年龄 (>55岁或≤55岁)以及患者是否复治。 表1为原始调查表格[1]。

表1 两组患者化疗后有效的人数a

文献[2]应用CMHχ2检验对表1中的数据进行了分析，结果显示，在以年龄和复治情况为分层因素的基础上，两组患者的疗效差异有统计学意义。但在对分层因素(年龄和复治)进行各层优势比齐性Breslow-Day检验时发现，各分层因素在效应方向上不一致，表明运用CMHχ2检验获得的结果并不可靠。本文在文献[2]的基础上，继续分析本案例，阐述多重logistic回归分析的正确应用、SAS软件实现及结果解释。

3 分析思路

本研究的分析思路为：首先应弄清数据结构，资料中涉及的影响因素包括治疗方案、年龄、是否为复治；因变量为治疗是否有效，故称为因变量为二值变量的四维列联表资料。处理此种资料可以选择的统计分析方法有加权χ2检验(限三维列联表)、CMHχ2检验、logistic回归分析和对数线性模型分析。由文献[2]的分析可见，本案例数据采用CMHχ2检验进行分析无法得出可靠结论，故采用二值变量的多重logistic回归分析为宜。

3.1 原始数据记录表向标准型表格的转换 根据资料类型以及要选择的统计分析方法，将原始表1转换为用于统计分析的标准型表格(表2)[2]。在转换表格的过程中，应该把同一因素不同水平组合下因变量在各水平下的频数全部呈现出来。

3.2 多重logistic回归分析的SAS实现

3.2.1 程序编写 SAS程序如下，程序名为LOG1.SAS。

程序说明：自变量a、b、c均为二值变量，因变量Y也是二值变量，故程序中变量赋值均以0和1来代表每个变量的两种状态。a表示年龄分层，a=0表示>55岁，a=1表示≤55岁；b表示复治与否，b=0表示复治，b=1表示初治；c表示用药方案，c=0表示多西他赛联合奥沙利铂，c=1表示多西他赛联合顺铂；Y=0表示有效，Y=1表示无效；变量f表示频数。数据的分析采用logistic过程，在Model语句中依次列出年龄、复治情况和用药方案。Model语句后面的“selection=stepwise”表示用逐步法筛选变量。Ods html语句则要求将数据处理结果以网页格式输出。SAS在拟合非条件logistic回归模型时，若不特别指定，计算的结果是与“Y=0”对应的概率表达式Z中的参数估计值，即应当写成P(Y=0)=[exp(Z)]/[1+exp(Z)]。此处需要注意的是，若自变量中有多值名义变量，则需要引入哑变量来取代多值名义变量，哑变量个数为该多值名义变量的水平数减1。

表2因变量为二值变量的四维列联表资料的标准型表格

Table2Standardtableofthefour-dimensionalcontingencytablewithabinarydependentvariable

a()>5576 468 2028 1220 20≤5568 1248 328 2012 16

a:对照组治疗方案为多西他赛联合顺铂，治疗组治疗方案为多西他赛联合奥沙利铂

SAS程序编写

3.2.2 结果输出及解释 第一部分：logistic过程产生的第一部分结果，主要是模型信息和关于因变量的说明，其中数据集名称为WORK.LOG1，因变量名称为Y，因变量有两个水平，权重变量为w，使用的模型是二值logit模型，参数估计时的优化方法是Fisher’s scoring法。读入观测数和使用观测数都是16，读入和使用的样本例数是464例(见表3)。因变量的取值顺序为0和1，各自分别有328例和136例(见表4)。最后一行文字说明该模型是以Y=0为基础，也就是以有效的概率为基础建模。这里需要注意的是， 在logistic过程中，默认状态下是以因变量取值较小的那个水平的发生概率为基础建模。本例中使用Y=0代表治疗有效，所以是以治疗有效为基础建立概率模型。

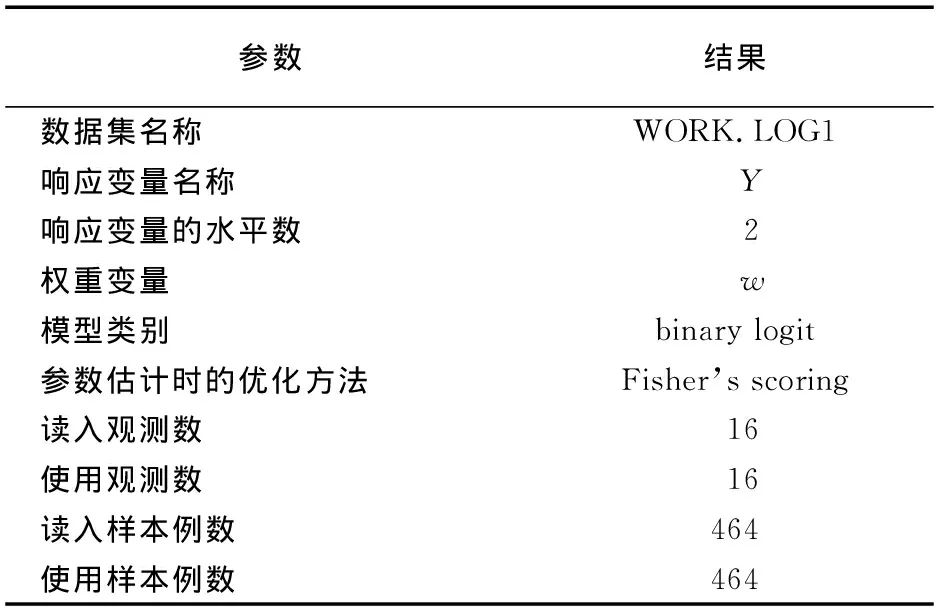
表3 Logistic过程中的模型信息

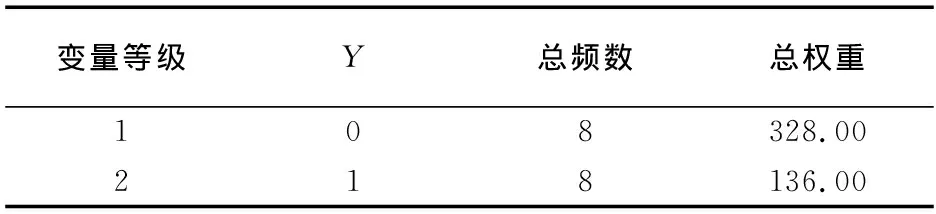
表4 响应变量统计结果

第二部分：对模型拟合优度进行检验。模型拟合统计量包括AIC、SC和-2倍的对数似然值，这三个统计量取值越小，表明模型拟合优度越好(见表5)。检验结果可见，在包含自变量的模型中，这三种方法计算的统计量取值都小于不包含自变量的模型，表明模型拟合得较好。因此，对回归模型整体是否成立进行假设：Beta=0，其原假设是所有的回归系数都为0，分别使用似然比检验、计分检验和Wald检验三种方法。检验结果中依次给出了χ2值、自由度(df值)和P值，3种方法的P值都<0.001，可以认为该模型是成立的(见表6)。

第三部分：在对拟合多重logistic回归分析方程过程中的变量进行筛选时，一般只保留对因变量有统计学意义的变量。这部分结果是回归系数以及优势比的估计结果。逐步回归法筛选变量的结果显示，a、b、c都是有统计学意义的变量(P<0.000 1)，均被保留在回归方程中(见表7)。由此可以写出治疗有效的概率表达式为：

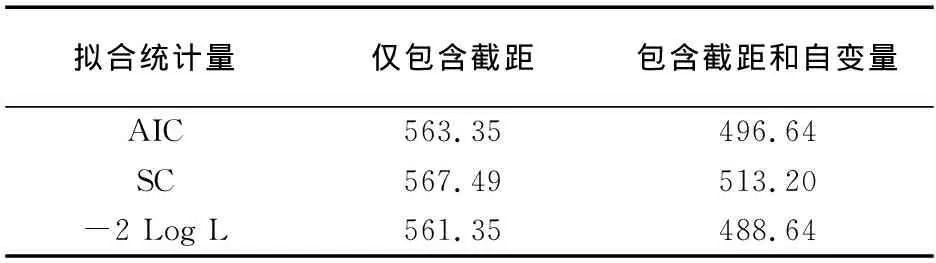
表5 模型拟合优度检验结果

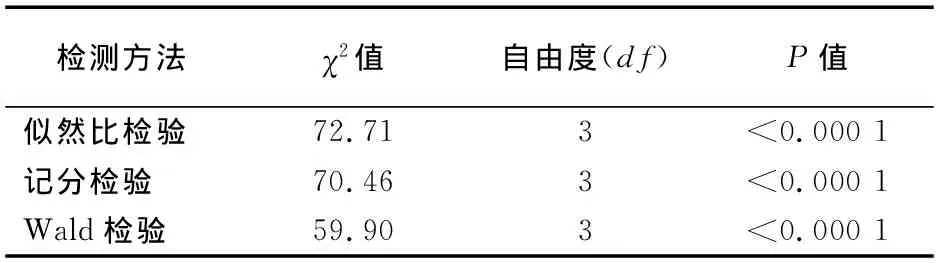
表6 对回归模型整体是否成立进行假设检验的结果

表7 最大似然比检验结果

计算优势比估计值发现，>55岁的患者接受治疗后有效的可能性是≤55岁者的0.391倍(95% CI为0.250～0.611)；复治的患者接受治疗后有效的可能性是初治患者的0.212倍(95% CI 为0.134～0.337)；接受多西他赛联合奥沙利铂治疗有效的可能性是多西他赛联合顺铂者的0.386倍(95% CI为0.247～0.605)，即多西他赛联合顺铂的疗效优于多西他赛联合奥沙利铂。以下所有OR的区间均不包含1，提示OR与1之间的差异有统计学意义。

最后输出预测概率和响应变量之间的关联性，其中统计量c的取值等于ROC曲线的曲线下面积(AUC)，是反映模型预测准确性的另外一个指标。计算得到c=0.747，表明该模型的预测效果较好(见表8)。

4 讨 论

近年来，logistic回归分析在众多的临床医学研究中得到了应用[3-6]，多数研究采用logistic回归分析模型进行预测分析，呈现出以下几个问题。(1)缺乏实用性：多数研究仅筛选出危险因素，却没有进一步列出预测模型，从而使得筛选出的危险因素缺乏利用度和推广性[3，4]。(2)缺乏模型拟合优度检验：与冯国双等[7]分析111篇应用logistic回归分析的文章提出的问题相一致，许多logistic回归分析均缺乏模型拟合优度检验。评价模型的基本要点是稳定性和准确性。在建立回归方程以后，需要对模型做出评价，即考察模型与实际数据的符合情况。除了采用评价拟合优度的主要统计量，如Pearson χ2值、偏差、Hosmer-Lemeshow统计量和一些信息测量指标以外，在模型的应用后期，可以建立验证集(validation set)对模型的准确度进行前瞻性的考察[6]。(3)用ROC曲线评价模型拟合优度：在SAS 9.2统计软件中，可以采用“ODS Statistical Graphics”功能绘制ROC曲线。根据ROC曲线与45度线的偏离程度反映模型预测效果，其优点在于直观，不足之处是不够精确。ROC曲线中，45度线下面积为0.5，ROC曲线与其偏离越大，就越向左上方靠拢，它下面的面积(AUC)也应该越大。SAS的logistic回归分析结果报告的“Association Statistics”中指标c是Wilcoxon-Mann-Whitney检验的统计量，等价于ROC曲线的AUC，是反映模型预测准确度的另外一种方式。

表8 预测概率与响应变量之间的关联性

本文采用logistic回归分析对患者(分层因素：年龄、是否复治)接受多西他赛联合奥沙利铂治疗和多西他赛联合顺铂治疗的疗效进行了分析，结果显示年龄、复治情况和用药方案都是对疗效有统计学意义的影响因素，根据三个因素建立的模型预测准确度较好。

【参考文献】

[1] 裘光贤，周兆春，王 婕.多西他赛联合奥沙利铂治疗晚期非小细胞肺癌的疗效和安全性[J].药学服务与研究,2011,11(3):210-212.

Qiu GuangXian,Zhou ZhaoChun,Wang Jie.Efficacy and safety of docetaxel combined with oxaliplatin in treatment of patients with advanced non-small-cell lung cancer[J].Pharm Care Res,2011,11(3):210-212.In Chinese with English abstract.

[2] 胡良平,沈 宁.用SAS软件实现高维列联表资料的统计学分析：CMH χ2检验[J].药学服务与研究,2013,13(5):332-335.

Hu LiangPing,Shen Ning.Statistical analysis and SAS solutions for multi-dimensional contingency table:CMH χ2test[J].Pharm Care Res,2013,13(5):332-335.In Chinese with English abstract.

[3] 胡晓斌，杨轶男，白亚娜.兰州市6825例住院孕产妇不良妊娠结局危险因素的logistic回归分析[J].中国循证医学杂志,2011,11(5):505-507.

Hu XiaoBin,Yang YiNan,Bai YaNa.Risk factor logistic regression on adverse pregnancy outcomes in 6825 hospitalized pregnant women in Lanzhou city[J].Chin J Evid-based Med,2011,11(5):505-507.In Chinese with English abstract.

[4] 李庆祥,张 莹,朱小玲,等.心肌梗死患者非酒精性脂肪性肝病的发生率及危险因素分析[J].中国循证医学杂志,2013,13(4):404-408.

Li QingXiang,Zhang Ying,Zhu XiaoLing,etal.Incidence and risk factors of myocardial infarction complicated by non-alcoholic fatty liver disease[J].Chin J Evid-based Med,2013,13(4):404-408.In Chinese with English abstract.

[5] Kikuchi M,Mikami T,Sato T,etal.High Ki67,Bax,and thymidylate synthase expression well correlates with response to chemoradiation therapy in locally advanced rectal cancers:proposal of a logistic model for prediction[J].Br J Cancer,2009,101(1):116-123.

[6] Roberts E B,Grayson A D,Alahmar A E,etal.Predicting angiographic outcome in contemporary percutaneous coronary intervention:a lesion-specific logistic model[J].J Interv Cardiol,2010,23(4):394-400.

[7] 冯国双，陈景武，周春莲.Logistic回归应用中容易忽视的几个问题[J].中华流行病学杂志,2004,25(6):544-545.

Feng GuoShuang,Chen JingWu,Zhou ChunLian.Several problems easily ignored in applications of logistic regression [J].Chin J Epidemiol,2004,25(6):544-545.In Chinese.