例说编制数学题目的若干关注点

☉江南大学附属实验中学 钱云祥

在数学教学中，无论是课堂教学，还是单元测试，或是期中、期末考试，都离不开数学题目.关于数学题目的编制，许多一线教师虽然也在不时地做着相关的工作，但由于对相关理论的学习不够，致使实际命题操作中常常会暴露出诸多问题.这既不利于对学生进行有效的训练，也不利于对学生的学业水平进行科学的评价.基于这些思考，笔者形成此文，力图通过对一些实际案例的剖析，与广大一线教师一起透视数学题目编制中值得关注的若干要点，以期提高大家对数学题目编制的认识与理解.

一、不因“题小”而随意

对于填空题、选择题这样的常见题型，不少老师往往认为这是小题目，大可不必仔细推敲，于是在实际编制中常常显得过于随意.

案例1：－2的相反数为_______，它的倒数为______.

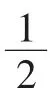
案例2：如图1，在四边形ABCD中，AB=4，BC=6，则当BD=____时，△ABD∽△DBC.

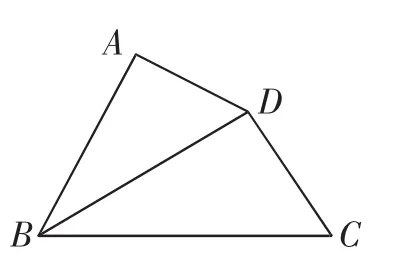
图1

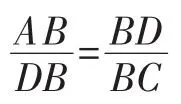
对于案例2中的问题，可以从两个角度入手去加以修改弥补.方法1：增加题干条件“BD平分∠ABC”，以使条件充分；方法2：改变题目设计方案，修改为：“如图1，在四边形ABCD中，AB=4，BC=6，若△ABD∽△DBC，则BD=_________.”这样，将结论与部分条件对换，从而使得条件充分.

从上述两个案例可以看出，教师在编制数学题目时，切忌因题目“小”而不重视，编制数学题目中的点滴随意，往往就会埋下祸根，或者造成歧义，或者导致错题出现.

二、不因“可解”而收笔

在编制数学题目时，需要教师对所编制的题目仔细推敲，反复打磨，然而不少老师只停留于“可解”的层面，往往因为自己似乎做出了“答案”，于是就匆匆收笔.

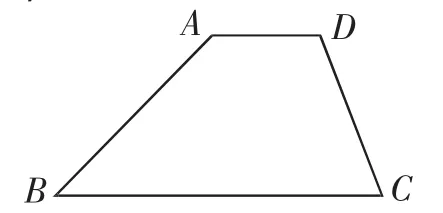
图2

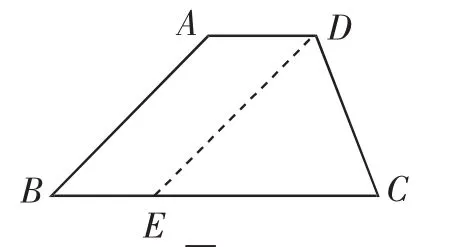
图3

案例3：如图2，在梯形ABCD中，AD∥BC，AD=3，AB=6，CD=5，∠B=40°，∠C=70°，求梯形ABCD的周长.

该题目所设置的问题是求梯形的周长.命题者预设了学生会添设如图3所示的辅助线，当给出梯形ABCD中∠B、∠C的度数之后，恰好能构成等腰三角形DEC，于是不难求得EC=DE=AB.当给出AD、AB的长度之后，即能求出BC的长.为求梯形ABCD的周长，还需知道CD的长，于是命题者在题干中又补充了条件CD=5.表面上看，条件充分，解答无误，但是本题却存在一处科学性错误.我们不妨来分析△DEC，由∠DEC=40°、∠EDC=∠C=70°可知这个三角形的形状被确定了，再加上EC=ED=6，其大小也被确定了.换句话说，由以上条件可知△DEC是一个形状、大小都已确定的三角形——根据三角函数的相关知识，不难求得CD=12cos70°.因此，CD的长又怎能再随意给定？也就是说，以上各项条件之间产生冲突.冲突造成的原因，是命题者在创设试题时，随意添加条件所致.由此可见，编制数学题目，切忌为了表面的“可解”而不断补充增加条件，切忌因为教师“能解”而认为题目编制大功告成.要知道，条件相互冲突的题目，本身就是错题，又何谈“可解”呢？

三、不为“求全”而拼凑

在数学题目的编制中，有些老师为了能在一道题中考查多个知识点，常常会把若干道题目进行组合，这本无可厚非.然而，为了过于“求全”而拼凑，则往往难以达成预设的考查目标，反而会适得其反，产生消极影响.

案例4：（某校九年级第二学期中考专题复习课的一道课外作业题）

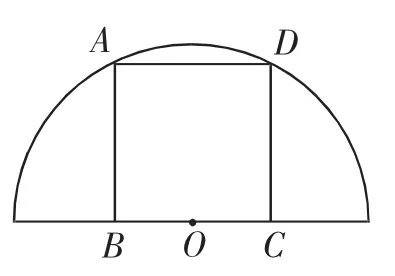
图4

（1）从邻居处得知蟹苗的放养密度为3只/平方米，这下他犯愁了：得买多少只蟹苗呢？请你帮他算一算.

（2）秋天到了，老王看着长大的螃蟹，心里美滋滋的，他想估计螃蟹的总质量.于是，经高人指点，老王从池塘中随意捞了20只螃蟹，称得质量分别如下（单位：克）：

210 240 190 210 320 180 250 220 240 250

300 220 300 240 210 220 160 220 240 240

①螃蟹质量的众数是__________克，平均每只质量为__________克；

②请你帮老王估计今年螃蟹的总质量（千克）.

（3）今年老王收入颇丰，他的胆子也大了起来，准备继续养殖螃蟹，同时在正方形区域ABCD的两边各围一片如图5所示的正方形区域养鳝鱼，如果鳝苗的放养密度为60条/平方米，你能再告诉老王需要买多少条鳝鱼苗吗？

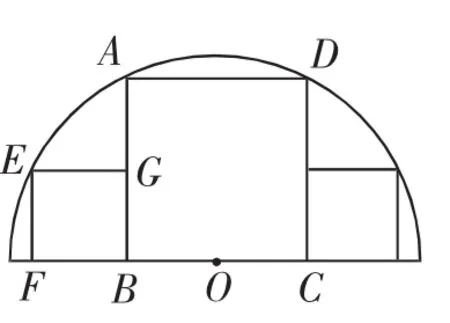
图5

（4）鳝鱼苗放养成熟后，经测算，成年鳝鱼一条重约30克.

①为了测算鳝鱼的成活率，老王从池塘里捕上500条鳝鱼做上标记，然后放回池塘里去，待带标记的鳝鱼完全混合于鳝鱼后，再次捕上300条鳝鱼，其中有标记的鳝鱼有15条，请你帮老王计算一下鳝鱼的成活率.（精确到1%）

②老王以12元/500克的价格将这些鳝鱼出售后，心里总是觉得不踏实，不知这些鳝鱼有没有赚到钱，于是，他统计了养殖鳝鱼的总支出（如表所示），请你帮他算一算盈亏情况.

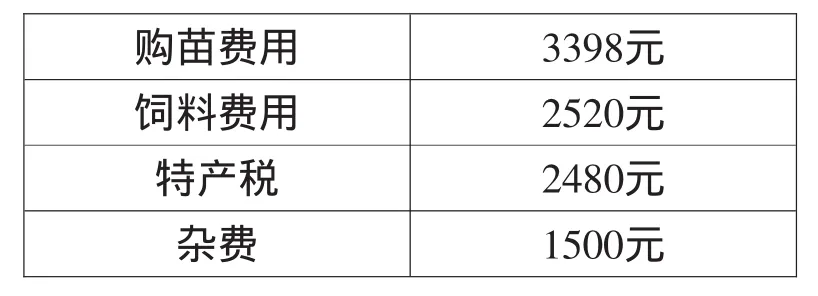
购苗费用 3398元饲料费用 2520元特产税 2480元杂费 1500元

（5）老王吸取了养鳝鱼的经验，开始关注历年螃蟹销售的市场行情了.由资料得知，从十月一日起的100天内，螃蟹的市场售价y1（单位：元/千克）与上市时间x（单位：天）的关系可用图6中的一条线段表示；螃蟹的养殖成本y2（单位：元/千克）与上市时间x（单位：天）的关系是

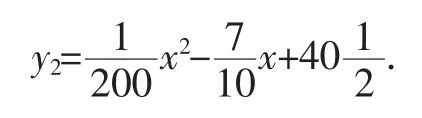
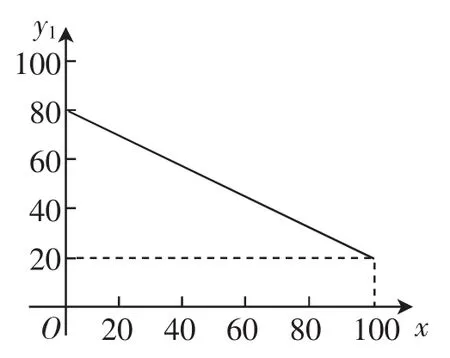
图6

①写出y1与x之间的关系式；

②如果认定市场售价减去养殖成本为纯收益，那么老王何时出售螃蟹收益最大？

这是道应用类综合题，考查了圆中的相关计算、勾股定理的应用、相关统计量的计算、用样本估计总体、用待定系数法求一次函数的解析式、二次函数的最值等知识点.尽管试题取材于现实生活，富有现实意义，但是这些内容在一道题目中一股脑儿地呈现出来，使得题目看上去十分庞杂臃肿，整道题目给人的感觉就是“到底有完没完”.试想，面对这样的题目，学生的心态究竟如何？

由此可见，为“求全”而拼凑的题目，一方面，在形式上没有美感；另一方面，会给学生造成心理压力，不利于学生良好学习品质的形成.

四、不为“求难”而刁难

在编制数学题时，不少老师总觉得似乎题目不带点难度就不过瘾，于是就刻意地编制了一些“难题”，实际效果如何呢？也许与命题者的初衷并不一致.

案例5：在四边形ABCD中，O为AC、BD的交点，现有下列四个条件：①AD∥BC，②AB=CD，③OA=OC，④∠ABC=∠ADC.给出以下6种组合：（1）①②；（2）①③；（3）①④；（4）②③；（5）②④；（6）③④.其中，能判定四边形ABCD是平行四边形的所有组合为（ ）.

A.（2）（3）B.（2）（3）（4）

C.（2）（3）（6）D.以上都不正确

显然，组合（1）无法推得四边形ABCD为平行四边形，反例为“等腰梯形”；由组合（2）或（3）易证得四边形ABCD为平行四边形；至于其他的3种组合，对于绝大多数学生而言，很难判断能否推得四边形ABCD是否为平行四边形，因为他们一方面很难想到具体的证明方法，另一方面也很难举出反例.分析到这里，对比四个选项，发现它们都有可能是正确项.接下来怎么办？难道是猜？显然，这绝非命题者的本意.

事实上，组合（4）、（5）都无法推得四边形ABCD是否为平行四边形.反例分别如图7、图8所示.限于篇幅，具体说明略.

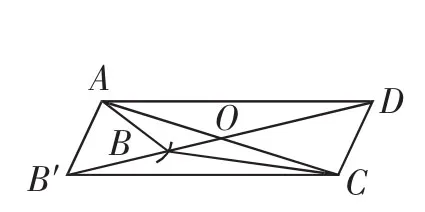
图7

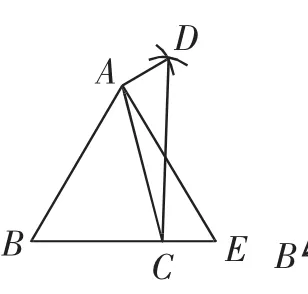
图8

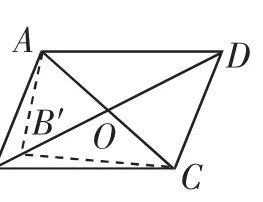
图9

而组合（6），则可用反证法予以证明.如图9，在四边形ABCD中，有OA=OC，∠ABC=∠ADC，假设四边形ABCD不是平行四边形，则OB≠OD（否则由OA=OC、OB=OD可得四边形ABCD是平行四边形）.不妨设OB＞OD，则可在OB上截取OB′=OD，连接AB′、CB′，易证四边形AB′CD为平行四边形，从而得到∠AB′C=∠ADC.又因为∠ABC=∠ADC，所以∠AB′C=∠ABC.另一方面，由于∠AB′D＞∠ABD，∠CB′D＞∠CBD，故∠AB′D+∠CB′D＞∠ABD+∠CBD，即∠AB′C＞∠ABC.从而产生矛盾，所以假设“四边形ABCD不是平行四边形”错误，故四边形ABCD是平行四边形.

综合以上分析，最后得出正确选项为“C”.不过，我们设身处地地换位思考，学生在独立完成此题时，是否有能力用相应的方法来解答这道选择题？如果不能，那么我们命制这样的题目去训练学生又有什么价值？编制题目让学生进行训练，其目的是为了发展学生，而非打击学生学习数学的兴趣和自信心.所以说，编制题目中的刻意“求难”，其实是刁难.

五、不为“情景”而变味

为体现数学的应用性，在编制数学题目时，命题者常常需要添加一定的问题情境.然而，若不能较好地理解与把握，则可能步入为情景而情景的怪圈，从而使得好好的数学题变了味.

案例6：某人从地下2楼乘电梯到地上8楼，共上升了________层楼.

仔细分析这道填空题，足见命题者在创设情景方面确实动了番脑筋.看似简单的一道数学题，其答案为上升了9层楼，而非10层楼.考查了什么知识？是8比－2大几吗？不是！这道题颇有脑筋急转弯的味道——不存在0楼.显然，这道题作为数学题而言，价值不大，对学生的数学思维训练毫无意义.学科性原则要求所命制的数学题，应该体现数学本身的学科知识和内涵，切不可为了情景而情景，结果过于哗众取宠而丢失了应有的数学味.

结语：编制数学题目，大有讲究.好的题目，必然需要在人文性、学科性、趣味性、应用性、科学性、导向性等方面把握得当.科学地命题，既能加强对学生知识与技能的训练，又能对学生的学习状况进行测量与评价，即根据相对客观与标准化的测量结果，结合一定的标准，教师可对学生的学习水平作出相应的评价.所以说，命题质量的高低，将直接影响教学的有效性与评价的科学性.为了提升题目的编制质量，教师确有必要加强这方面的自我修养，以更好地促进学生的发展.

1.钟玖珍，庞彦福.初三数学总复习策略再探——谈二轮复习的选题原则、方法和评价［J］.中学数学（下），2013（11）.

2.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

3.钱云祥.有效学业评价——初中数学练习测试命题问题诊断与指导 ［M］.长春：东北师范大学出版社，2011.