初中数学教学中几何直观能力培养探析
2014-07-25江苏省苏州市相城区东桥中学周海东
☉江苏省苏州市相城区东桥中学 周海东
《义务教育数学课程标准(2011年版)》中指出:“在数学课程中,应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想.”[1]当前,几何直观正成为数学教学研究中生动的、不断增长的而且迷人的课题.[2]正如荷兰数学家弗莱登塔尔所说:“几何直观能告诉我们什么是可能重要、可能有意义和可接近的,并使我们在课题、概念与方法的荒漠之中免于陷入歧途之苦.”在初中数学课堂教学中,充分利用几何直观来揭示研究对象的性质和关系,使学生认识几何直观在数学学习中的意义和作用,创造出属于自己的学习方式,这是初中数学几何直观教学的核心所在.那么,如何理解几何直观?特别是在初中数学教学中,如何渗透几何直观的意识和能力呢?下面笔者就结合自己的教学实践,谈谈自己的理解与看法.
一、几何直观的含义及表现形式
对于几何直观,徐利治教授认为:“几何直观是借助于见到的或想到的几何图形的形象关系产生对数量关系的直接感知.”[3]《数学课程标准》则指出:“几何直观主要是指利用图形描述和分析问题.”简单的说,几何直观就是借助于看到的(或想象出来的)几何图形的形象关系,对数量关系和空间形式进行直接感知、整体把握的能力.主要包括空间想象能力、直观洞察能力和用“图形语言”来思考问题的能力.
借助几何直观,可以把复杂的数学问题,变得简明、形象,有助于探索解决问题的思路,预测结果.用最通俗的话说几何直观,就是看图想事,看图说理.在数学新课改中,几何直观被看成是贯穿数学课堂教学的主要线索之一.在初中数学中,整式的乘除、一元二次方程的基本概念、直角坐标系与点的位置、已知变量的值求函数值、基本函数的概念与性质、特殊三角函数、圆、点的坐标等知识的学习,都离不开几何直观.
几何直观是在直观感知的感性基础之上所形成的理性思考的结果,是学习者对于数学对象的几何属性的整体把握和直接判断,从几何直观的表现形式来看,几何直观主要表现为实物直观、符号直观、图形直观和替代物直观四种形式.[4]
二、培养和发展学生几何直观能力的实践
我国著名的数学家华罗庚说:“形缺数时难入微,数缺形时少直观”.几何直观是揭示现代数学本质的有力工具,要培养和发展学生的几何直观,需要依托具体的数学课程教学内容,需要具体落实在课程内容、课堂教学细节之中.
(一)重视图景体验,培养学生的空间想象能力
中学数学中的空间想象能力主要是指:学生对客观事物的空间形式进行观察、分析、抽象思考和创新的能力.初中学生往往缺乏生活经验,因而对几何图形缺少直观,缺少体验.体验是一种图景思维,不同于经验,它不仅仅重视主体的心理结构,而且在经验的基础上更注重主体与客体合一的动态建构.也就是说,它是亲身经历,是通过实践来认识周围事物的一种活动.对于初中学生而言,空间想象能力是在图景体验的过程中逐步建立起来的.学生的图景体验是他们发展空间想象能力的基础.初中数学课堂中常见的图景体验途径有生活经验的再现,实物观察活动,操作活动等.在这些活动中,学生感知和体验空间与图形的现实意义,初步体验数与形的联系,逐步培养学生的空间想象能力.
1.进行表象积累,增强感性认识
我们知道一个人头脑中旧形象的素材越多,构成新形象的可能性就越大,想象能力也就越丰富,头脑中旧形象的素材越少,想象能力也就越差,可见有效的表象积累是培养想象能力的关键.因此要让学生将所学的知识与生活经验产生联想,就必须通过表象积累来提高学生对几何图形的感性认识.比如:苏科版八(下)图形的相似中关于投影的教学.中心投影,平行投影这些概念和学生的生活实际联系比较密切,课堂上笔者引导学生去观察日常生活当中日光下的影子,灯光下的影子.这实际上就是一个物体和它的投影之间的关系.阳光可以看成是平行投影,灯光,可以看成是中心投影了,这个点光源就是中心投影.通过表象的积累,也增强学生对投影的感性认识.有的时候我们成人把投影想的很复杂.其实对于初中学生来说倒没有那么复杂,这些概念,经过“直观”后,就很容易理解了.
2.构建操作实验,获得感官经验
空间想象力的培养,仅靠观察是不够的,几何直观能力既然作为一种个体的感觉判断能力,是需在不断的动手操作中去感受和体会的.也正因为如此,在初中数学教学中,教师要注重引导学生参与到课堂学习中,在活动中来探究,在探究中获得认知、感受和体会.教师还必须引导学生自己进行独立的操作实验活动,让他们去比一比,折一折,剪一剪,拼一拼、画一画.通过视觉、触觉、听觉等多种分析器官共同参与的操作活动,验证一些原有的猜想或者产生一些新的发现.这种“直观”比老师的说教有效得多.
3.适当运用多媒体演示,拓展空间想象能力
多媒体演示形象具体,声色兼备,动静结合,恰当地运用,可以变抽象为具体,调动学生各种感官协同作用,拓展学生的空间想象能力.由于条件的限制,我们不可能把所有想到的东西都带到课堂上来,但我们可以事先把这些物体拍成照片或视频,放入电脑,课上运用多媒体来展示验证想象,体验想象的可靠性、正确性.尤其是一些学生很难体验或想象的动态效果,我们可以通过动画设计来演示运动的过程,变不可能为可能,通过图、色、音和动画让学生一目了然.运用动画,结合多媒体综合技术演示,拓展了学生的思维动态想象空间.
(二)观察与思考并重,培养学生的直观洞察能力
几何学习中,学生的直观洞察能力非常重要,这种能力实质上是对几何图形及其结构、关系的想象和判断.类似于猜想,主要表现为灵感和顿悟.从某种意义上来说,几何教学中教师既要关注学生表征问题的过程,更要关注表征之后的反思与顿悟.没有反思与顿悟,学生可能获得了几何的方法,却未必能获得“几何直观”的能力.要培养学生的直观洞察能力,要注意以下几个方面:
1.要重视学生基础知识的训练
扎实的基础知识是产生直觉的源泉,没有深厚的功底,是不会迸发出直觉的思维,也就无法提高学生的直观洞察力.因此,教学中要严格要求学生理解定义,熟练掌握图形的性质和定理.
2.要注重引导学生进行合理猜想
真正的科学探究应是建立在思维的逻辑性和科学性基础上的有效探究.而有效探究的实施前提是必须建立在提出符合逻辑性和科学性的合理猜想的基础之上.正如牛顿所说:“没有大胆的猜想,就做不出伟大的发现.”猜想既是激发学生学习兴趣的手段,又是发展学生直觉思维的有效途径,还是学生掌握探求知识、方法的必要手段.在教学中,我们一方面要注意保护学生既有的猜想和直觉能力,另一方面要注意引导学生学会合理猜想的方法,并不断使他们的直观洞察能力得到发展.在教学中,还要注意引导学生大胆设问;引导学生敢于发表自己的见解;引导学生充分活动.让学生通过猜想来“触摸”相关的研究对象.
3.要注意观察与思考并重
直观洞察力的产生要依赖于对几何图形全面及本质的把握.没有观察就没有发现,更不会有创造.但观察必须与思考相结合,没有思考的观察就不是真正意义的观察.在观察之前,要给学生明确且具体的目的、任务和要求.观察要细致,思考需用心,这样才能发现问题和解决问题.
(三)用“图”说话,培养学生用“图形语言”来思考问题的能力
希尔伯特在《直观几何》中曾谈到:“图形可以帮助刻画和描述问题,一旦用图形把一个问题描述清楚,就有可能使这个问题变得直观、简单.”用图形“说话”,用图形描述问题,用图形讨论问题,这是一种基本的数学素质.那么,在教学中如何培养学生用“图形语言”来思考问题的能力呢?
1.重视图感训练,培养学生的读图、作图能力
几何直观在本质上是一种通过图形所展开想象的能力,它与许多重要的数学内容紧密相连.因此,我们在教学中应重视学生“图感”的训练.在日常的教学中,要帮助学生从小养成良好的画图习惯.在教学中要通过多种途径和方式使学生真正体会画图对理解概念、寻求解决思路带来的益处.要求学生解决问题时能画图的尽量画图,将相对抽象的思考对象“图形化”,尽量把数学的过程变得直观,直观了就容易展开形象思维.作为教师要从思想上认识到它的重要性,并把它当作是最基本的能力去培养学生.
2.重视三种几何语言的转化,培养学生用图形说话的能力
几何语言的基本形式有:图形语言、文字语言、符号语言.这三种语言在几何中是并存的,通常又是相互渗透和转化的.由于这三种语言的特点不同,在几何教学中所发挥的作用也不同.图形语言形象、直观,能帮助学生认识问题和理解问题.因此,在例题、习题的讲解中,要训练学生学会把文字语言符号化,已知条件图形化,学会用图形说话.为了让学生能更好地将题和图有机统一,教学中可以采用各种不同的符号将已知条件在图形中表示出来,使条件更加直观.
3.重视数形结合,培养学生用“图形”思考问题
数形结合是研究数学和数学教学中的重要思维原则之一.几何直观与数学的内容紧密相连.一些重要的数学内容、概念,例如数轴、函数,高中的解析几何,向量等,都具有“双重性”,既有“数的特征”,也有“形的特征”.数形结合就是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合起来,实现抽象概念与具体形象、表象的联系和转化,化难为易,化抽象为直观.
分析:这道题如果用代数方法解决相当困难,但我们可以用几何的方法将这道题直观出来.
解:如图1,设P(x,0)、E(2,2)、F(3,1),则
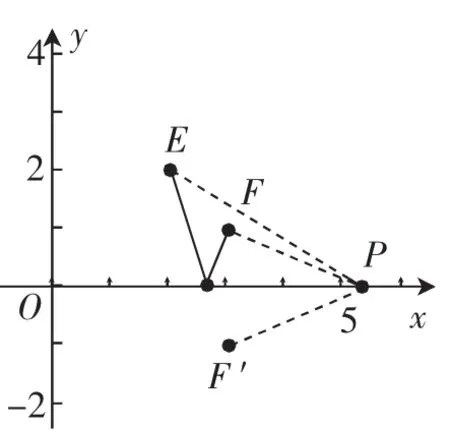
图1
所以y=PE+PF.
因此求y的最小值,实质是求(PE+PF)的最小值.
点评:这样我们就将数学语言与直观的几何图形结合了起来.在应用转化策略解决问题的同时,巧妙借助几何直观,把复杂的问题转化成简单的问题,可以培养学生初步的几何直观能力.
三、培养和发展学生几何直观能力的误区
培养和发展学生几何直观能力还要注意以下几个容易被我们忽视的误区.
1.为了直观而直观
在课堂上引进直观手段的目的是为了使学生摆脱形象思维,最终形成抽象思维.当运用直观手段在帮助学生形成对知识的信任,形成一定的感性经验后,我们就要使学生摆脱它,而将学生的思维引导到抽象思维上去.然而,在实际教学中我们常常会遇到这样两种情况:一是直观教具以其某一个细节束缚住了学生的注意力,二是直观的结论学生已知,根本没有探究的兴趣.这两种情形下几何直观不仅没有帮助反而妨碍了学生去思考老师本来想引导他们去思考的抽象真理.所以说,几何直观应当使学生把注意力放在最主要、最本质的东西上去.虽然直观教学可以收到事半功倍之效,但是如果滥用直观手段,也会阻碍学生思维的发展.因此,教师教学中需注意不要为了直观而引进直观.
2.要注意误差的干扰
在运用几何直观的实际教学中,许多学生往往由于画图不准确、讨论不全面等原因导致出错,或有一定的误差干扰,失去数学问题原有的科学性与严密性,甚至不能得出正确结论.比如,在讲授黄金分割时,为了说明课本的宽与长满足黄金比,教材设计了“量一量”这一环节,你若让学生真的量一量,问题就出来了,宽与长的比各种答案都有,而且与0.618相差甚远.其实,原因就在于误差的干扰,由于学生测量工具或测量方法的精确度有限,导致产生了较大的误差,使正确结论无法呈现,反而干扰了学生的思维.
3.要注意直观背后的数学理性
直观并不只是为了让学生获得直观的感受,其最终目的是为了引导学生从数学的角度去进行理性思考,通过抽象提升得出数学结论.美国魔术师保罗·卡瑞曾经提出这样的一个问题:如图2是这个正方形可以按图中标出的数据分割成五块几何图形,剪开后重新拼接成图3,奇怪,怎么又多出了一个洞!这次斜线处并无叠合,少掉的一个单位面积哪里去了呢?[5]

图2
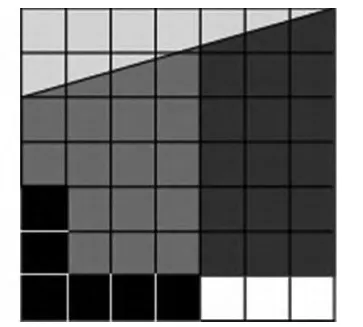
图3
从直观来看,这个问题中的图2和图3是矛盾的,但其背后隐藏着的数学理性却告诉我们,其实左右两块深灰色色块和浅灰色色块并不全等,这就不是能直观看出来的了,需要依据计算才能说明.因此,我们在引入直观的时候要注意直观背后的数学理性.
几何直观的培养不是一朝一夕的事,在教学中,应根据学生的认识规律,采用多种教学手段,教学方法,引导学生运用多种感官积极主动地参与到教学中来,协调活动,促使学生对几何形体有深刻的认识,使几何形体在头脑中从“简约”走向“丰盈”,这样才能更有效地培养学生的空间观念和几何直观.
1.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
2.秦德生,孔凡哲.关于几何直观的思考[J].中学数学教学参考(中),2005(10).
3.徐利治.谈谈我的一些数学治学经验[J].数学通报,2000(5).
4.孔凡哲,史宁中.关于几何直观的含义与表现形式[J].课程教材教法,2012(7).
5.欺骗眼睛的几何问题.http://learning.sohu.com/20060208/n241706703.shtml.
