培养问题意识推开问题大门——“线段、射线、直线（第1课时）”的教学实录及其点评

☉江苏省泰兴市黄桥初级中学 黄玉华（执教）

☉江苏省兴化市教育局教研室 陈德前（点评）

在江苏省第四届“心桥杯”六校教改联盟（黄桥）——“推开问题的大门”课堂教学研讨活动中，笔者执教的课题苏科版《数学》七年级上册第六章第一节“线段、射线、直线（第1课时）”，赢得了与会教师的高度评价，在此与各位同行分享交流.

一、教学实录与点评

1.创设情境，温故知新

教师：请同学们欣赏章头图、旗杆、探照灯发出的光线、向两个方向无限延伸的铁路，你能从图中找出哪些熟悉的图形？

学生1：线段，射线，直线，三角形……

教师：很好！本节课，我们就来进一步认识“线段、射线、直线”.（板书课题）

教师：请两名同学到黑板上各画出一条线段、射线和直线，其他同学在下面完成，议一议它们的区别.

学生2：线段有两个端点，射线只有一个端点，直线没有端点.

学生3：线段不能延伸，射线只能向一个方向延伸，直线可以向两个方向延伸，线段有长度，射线和直线没有长度.

教师：那么如何区别黑板上两条不同的线段、射线、直线呢？本节课我们就一起来学习它们的表示.

点评：通过对章头图和生活中常见图形的阅读，让学生从中发现许多他们所熟悉的图形，体会生活中的许多美妙的图形都是由一些简单图形构成的，进而激发学生学好本节课内容的兴趣；通过设计如何区别线段、射线和直线的问题，调动学生如何表示它们的学习激情，又自然过渡到所要学习的新内容，新课学习的任务水到渠成.

2.问题引导，探求新知

教师：请同学们自学课本P146页最后一段内容到P147页第3行结束，尝试完成屏幕上的几个问题，并将刚才你画的线段、射线、直线用符号进行表示.为了让学生了解本课学习的内容及要能达到的目标，让学生带着问题自主阅读课本，教师在投影幕上先给出学生自学时的导学问题.

问题：（1）怎样用符号表示线段、射线和直线？表示的字母有什么注意点？有几种表示方法？

（2）怎样由一条线段得到射线？直线？你能用准确的语言描述出来吗？

教师：请同学们将学习过程中的问题提出来，小组内进行交流.

教师：刚才同学们学得很认真，交流也很激烈，下面来看看大家掌握得怎么样？线段怎样表示？

学生4：线段可以用表示端点的两个大写字母来表示，也可以用一个小写字母来表示，如甲同学画的线段可以记作线段AB、线段BA或线段a.

教师：对，所以表示线段的两个字母没有顺序！乙同学画的这条线段如何表示？

学生5：两个端点字母可以用大写字母C、D来表示，记为线段CD或线段DC，也可以用一个小写字母b来表示，记为线段b.

教师：请同学们看屏幕，你能用语言描述怎样由一条线段得到一条射线吗？（屏幕上展示的是将线段AB由A向B方向延长时得到一条射线的动画）

学生6：延长线段AB.

教师：描述很准确，这里延长线段AB是指按从点A到点B的方向延长.这条射线如何表示呢？

学生7：射线AB.

教师：能记为射线BA吗？

学生8：不能，因为表示射线的端点字母必须写在另一个字母的前面.

教师：请同学们看屏幕，你能用语言描述这一条射线怎样得来的吗？（屏幕上展示的是将线段AB由B向A方向延长时得到一条射线的动画）

学生9：延长线段BA.

教师：还可以怎样描述？

学生10：反向延长线段AB.

教师：对，反向延长线段AB是指按从点A到点B的方向的反方向即从点B到点A的方向延长.这条射线如何表示？

学生（齐）：射线BA.

教师：那么同学乙画的这条射线如何表示？

学生11：端点字母设为M，在这条射线上另取一点记为N，表示为射线MN.

教师：很好！如果再在这条射线取一个点为E，怎样表示？再取一点F呢？

学生（齐）：射线ME、射线MF.

教师：表示同一条射线有多少种不同的表示方法呢？

学生12：有无数种，只要用射线的端点和它延伸方向上再取一个点就可以表示.

教师：请同学们看屏幕，你能用语言描述这一条直线怎样得来的吗？（屏幕上展示的是将射线AB反向延长时得到一条直线的动画）

学生13：延长线段BA.

学生14：反向延长射线AB.

教师：同学们描述都非常正确，那直线怎样表示？

学生15：在直线上任取两个点A、B，记为直线AB或直线BA，也可以用一个小写字母m表示，记为直线m.

教师：和表示线段的两个字母类似，表示直线的两个字母没有顺序！

点评：设计问题串引导学生进行自主学习，不仅可以提高学生自主学习的效果，而且可以让学生在思考问题串时感受提出问题的方法，意在帮助学生进一步积累发现问题、提出问题的基本经验；在检查自主学习的成果时，教师再次精心设计问题串，引领学生的思维，把学生的思维不断引向深入——线段、射线、直线之间有什么联系与区别？如何用运动的观点来理解这种联系与区别？突出了数学的本质，为下面应用它们去解决有关问题奠定了基础.

3.练习巩固，应用新知

学生口答，教师追问.

（1）如图1.

图1

①射线OA与射线OB是同一条射线吗？

②射线OB与射线AB是同一条射线吗？

③射线OA与射线AO是同一条射线吗？

（2）请你判断下列说法是否正确.

（3）如图2，在直线m上有3个点A、B、C，图中以A为端点的线段有哪几条？

图2

教师：你能提出什么问题考考其他同学吗？

学生16：图中以B为端点的线段有哪几条？

学生17：有线段BA、线段BC.

学生18：图中共有多少条线段？

学生19：共有3条，线段AB、线段AC、线段BC.

学生20：图中以A为端点的射线有哪几条？

教师：这个问题提得很好，我们不仅学习了线段，还有射线和直线，谁来解决一下？

学生21：两条，从点A向右的射线可记为射线AB或射线AC，但向左的……（犹豫不决）

教师：从点A向左的是一条射线，但要表示它还需要再在点A左侧的射线上另取一点，才可表示，直线上的一个点将直线分成几条射线呢？

学生22：两条.

教师：还能提出什么问题吗？

学生23：图中以B为端点的射线有哪几条？

学生24：图中以C为端点的射线有哪几条？

学生25：图中共有多少条射线？

学生26：图中共有多少条直线？

……

（教室里沸腾起来了）

教师：同学们提出的问题真不少！如果在直线m上有n（n≥2）个点，那么图中共有多少条线段？多少条射线？请同学们课后去研究.

点评：对数学概念的认识，必须从正反两个方面进行强化，这里教者设计了一组问答题和判断题，有效地从正反两个方面帮助学生来强化对线段、射线、直线概念的理解，特别是对同一条射线必须满足两同（即端点相同，从端点射出去的方向相同）的认识；在这个基础上，利用图2，在教师先示范性地提出一个问题的基础上，让学生尝试着提出不同的问题，来着力培养学生的问题意识；由学生自己提出问题，具有一定的离散性，教师在此基础上，进行了归纳，提出了一个一般性的问题，并将问题的探索延伸至课外.

4.回归生活，深化新知

活动1：

教师：如图3，从甲地到乙地有3条路，走哪条路较近？

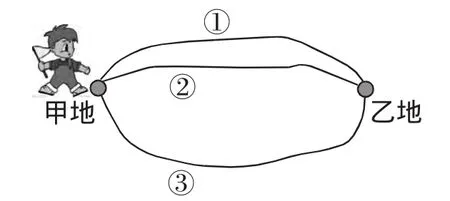
图3

学生（齐）：路线2.

教师：从甲地到乙地能否修一条最短的路？如果能，你认为这条路应该怎样修？请在图中画出这条路.

学生27：从甲地到乙地修一条线段.

教师：结合生活经验，同学们能概括出一个结论吗？

学生（齐）：两点之间线段最短.

教师：今后我们可以将这个结论作为说理的依据，下面我们来看它在生活中的应用.2005年之前，我们台湾同胞要从高雄机场赶到北京机场需要绕道香港机场，全程约为2654km，同学们觉得应该怎样设计航线行程最短呢？为什么？

学生28：从台湾直达北京，两点之间线段最短.

教师：对！经多方努力协商，2005年开通了台湾与北京的直航，全程约为2098km，不仅仅缩短海峡两岸的距离，更拉近了同胞们的心灵距离.你认为用哪一个数据来刻画北京与高雄两地的距离更为合理？

学生29：2098km.

教师：对，我们把连接两点所得线段的长度，叫做这两点之间的距离，所以北京与高雄的两地的距离就约为2098km，要注意两点之间的距离是连接两点的线段的长度，是一个数量，它与线段是不同的.

活动2：

教师：在纸上画出一点A，过点A你能画几条直线？

学生30（动手操作）：无数条.

教师：在纸上画出两点A、B，经过A、B两点你能画几条直线？

学生31（动手操作）：一条.

教师：我们也可以从生活经验中感知这一点，如果你想将一根细木条固定在墙上，至少需要几个钉子？

学生32：两个.

教师：所以经过两个点的直线有几条？

学生（齐）：一条.

教师：由此，我们又可以概括一个结论？

学生33：两点确定一条直线.

教师：这里的“确定”一词有两层含义，一是经过两点有一条直线，表示存在；另一层含义是经过两点的直线只有一条，表示唯一.这就是数学语言的简洁！下面，我们来看一个应用，每年的3月12日是植树节，你用什么方法可以使植的树在一条直线上？

学生33：只要定出两个树坑的位置就能确定同一行树所在的直线.

点评：这里主要安排了两个活动，活动1让学生联系实际生活经验来感受基本事实“两点之间线段最短”，然后应用这个基本事实来解决实际问题，进而得出了两点之间距离的概念，水到渠成；活动2则通过操作和对实际生活经验的感受得到了直线的基本性质“两点确定一条直线”，并应用这个基本事实解决了如何将“植的树在一条直线上”的实际问题，能使学生体会到所学知识的广泛应用，提高了学生应用数学知识解决实际问题的能力.

5.综合拓展，活化新知

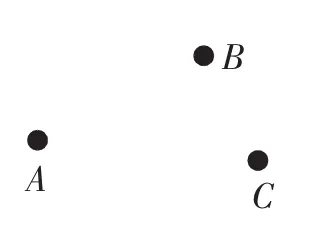
图4

出示三道练习题.

1.做一做：如图4，已知点A、B、C.

（1）画线段BC（连接BC）；

（2）画直线AB、AC；

（3）在线段BC上取一点D，画射线AD.

2.如图5，看图说话.

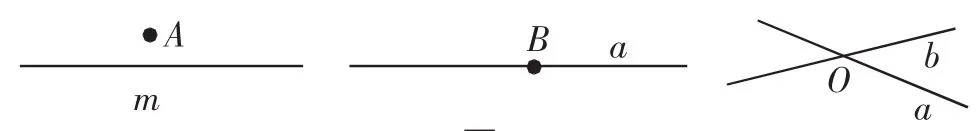
图5

3.赛一赛：看图、说图、画图.

比赛规则：同桌两名同学，一人面向屏幕，另一个人反向.其中一名同学看屏幕上提供的如图6所示的图形说给另一名同学听，另一名同学在纸上画出大致的图形，看哪一组完成的既对又快，然后两人互换角色.

（赛一赛，教室里再次沸腾）

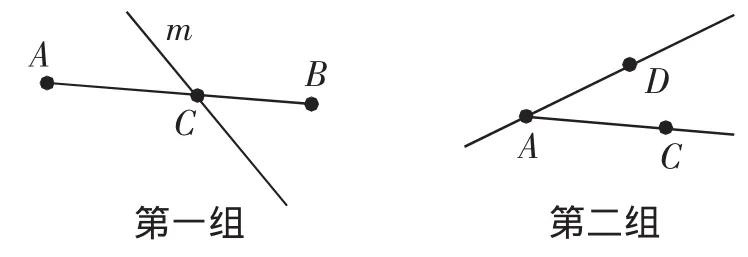
图6

点评：这里，第1题是读句画图，训练学生由符号语言转化为图形语言的能力；第2题是看图说话，训练学生由图形语言转化为符号语言的能力；第3题是综合运用题，考查学生三种语言相互转化的能力.

6.小结交流，感悟新知

学生自主小结线段、射线、直线的区别、符号表示、两个结论，学习过程中获得的经验和方法，在回顾和感悟中提升知识的运用能力.

教师：本节课的内容可提炼成“3332”，即学习了3种图形、3种概念、3个语言和2条结论，同学们还有什么问题吗？

学生34：过一个点可以画无数条直线，过两个点可以画一条直线，那么过3个点，4个点，…，可以画多少条直线呢？

教师：你提的问题真好！请大家课后去思考一下.本节课同学们不仅仅能解决老师提出的问题，而且还能积极主动的观察、思考发现问题，提出很多有价值的问题，推开了问题的大门，希望同学们认真学好数学知识，领会数学思想，培养问题意识，勇于创新，争取取得优异的成绩！谢谢大家.

点评：以问题串的形式引导学生进行总结反思，在学生自主小结的基础上，抓住线段、射线、直线的异同，教师及时进行了提炼，帮助学生形成知识网络“3332”；利用学生谈收获体会的契机，帮助学生积累基本活动经验；要求学生提出新的问题，有利于进一步培养学生的问题意识，也为下一节课的教学打下了基础.

二、总评

2011年版义务教育数学新课程标准提出：“通过义务教育阶段的数学学习，学生能体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，运用数学的思维方式进行思考，增强发现和提出问题的能力、分析和解决问题的能力.”爱因斯坦曾强调：“发现问题和系统阐述问题可能要比得到解答更为重要.解答可能仅仅是数学或实验技能问题，而提出新问题、新的可能性，从新的角度去考虑老问题，则要求创造性的想象，而且标志着科学的真正进步.”因此，在培养学生创新精神和实践能力的总体目标下，培养学生的问题意识，尤其是发现和提出问题的能力显得非常重要.

如何在数学教学中落实这个要求呢？这节课给我们以下很好的启示.

1.在研读教材中挖掘培养问题意识的素材

在课堂教学中，培养学生问题意识的素材从哪里来？教材中有着丰富的培养学生问题意识的素材.只有通过认真研读教材，加深对教材的理解，才能从教材中挖掘出培养学生问题意识的素材，这样才可以驾驭教材，进而根据实际情况来设计出有效培养学生问题意识的教学预案.通过研读教材，我们可以发现，在本节课的教学内容中，有许多培养问题意识的素材.正因为有了这样的研读、思考，所以在教学中，老师充分利用学生已有的线段、射线、直线的知识，以问题为载体，再引导学生发现问题，提出问题，进而分析问题和解决问题，培养了学生的问题意识，有效地建构了知识.

2.在学情分析中把握培养问题意识的梯度

研究学生，了解学生，全面掌握学情是提高数学课堂教学有效性的前提之一，是把握培养问题意识的梯度的基础.因此，要有效的培养学生的问题意识，教师应当对学生作出更为深入和具体的分析，为教师的备课及课堂教学的实施打下坚实的基础.

由于执教的学校是一所农村初中，学生不善于发表独立见解，发现和提出问题的能力、分析和解决问题的能力都比较弱，但他们具有很强的好奇心，对小学里关于“线段、射线、直线”的知识掌握较好，对线段、射线、直线这些图形的生活原型很熟悉，所以教者在教学中以生活中的线段、射线、直线模型为抓手，抓住前后知识的联系，充分利用学生的知识最近发展区，引导学生拾级而上，不断地发现和提出问题，并帮助他们学会有条理地分析和解决问题，积累初步的数学活动经验，达到了预期的教学目的.

3.在多元情境中提供培养问题意识的契机

问题是数学的心脏，而问题的发现和提出需要有好的问题情境.创设好的问题情境是开展数学教学活动的前提，它能起到思维的定向、激发欲望的作用.什么是好的问题情境？裴光亚先生作出了精辟的论述：愤、悱是对“问题情境”的恰当描述.愤，就是想求明白而感到困难；悱，就是想说出又说不明白.它不只是“问题”，在问题的背后，还有一种内在需求，一种学生主动探究的愿望.好的数学情境应具有三个特征：（1）应该是学生熟悉的；（2）应该是简明的；（3）应必然地引向数学的本质.应该说，这节课努力以问题为主线，注意启发引导学生思考，引导学生开展数学探究活动，使他们经历观察、实验、猜测、推理、交流、反思等理性思维的基本过程，使学生更加主动、有兴趣地学，富有探索性地学，逐步培养了学生的问题意识，孕育了创新精神.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.杨裕前，董林伟.义务教育课程标准实验教科书·数学（七年级上册）［M］.南京：江苏科技出版社，2012.

3.章建跃.数学教学目标再思考［J］.中国数学教育（初中版），2012（1）.

4.陈德前，徐秀峰.精心设计问题载体，培养学生问题意识——《相似三角形的应用（2）》课堂实录片段与点评［J］.中国数学教育（初中版），2013（10）.

5.刘东升，符永平.在“核心主线”规则下预设“生成”的自由——“探索三角形相似的条件（第1课时）”教学设计与点评［J］.中学数学（下），2013（3）.

6.陈德前.在解题教学中培养学生的创新思维［J］.中学数学（下），2012（1）.