APOS理论指导下的概念教学设计——以“锐角三角比的意义”为例
2014-07-25上海市外国语大学附属外国语学校李祯俊
☉上海市外国语大学附属外国语学校 李祯俊
☉上海市外国语大学附属外国语学校 李祯俊
一、问题的提出
李邦河院士曾说“数学根本上是玩概念的,不是玩技巧,技巧不足道也.”数学概念是数学理论大厦的基石,是中学生数学基础的重要组成部分.不依托于概念的解题训练犹如把高万丈高楼建于沙地,容易导致学生过于依赖技巧和模式,虽然能解题,但是缺乏举一反三的变通能力,非但不能“熟能生巧”反而“生厌”、“生笨”.事实上,掌握概念并运用概念进行判断和推理正是解题的关键,提高解题能力应该从重视概念教学开始.
APOS理论是美国数学家杜宾斯基于上世纪90年代提出的数学教育心理学理论,该理论是对皮亚杰的“反思性抽象”(Reflective abstraction)理论的拓展[1],其针对的正是数学概念的学习过程.APOS理论的四个字母分别代表了理解数学概念的四个阶段:Action(活动),Process(程序),Object(对象),Schema(图式).它揭示了学生在建构数学概念时的过程和层次,为教师提供了教学设计的具体模式和策略.
在美国及其他一些国家已有实验证明在APOS理论指导下设计的课程显著优于传统课程,而国内的研究还多停留在理论阶段.为了实现该理论与中国数学教学实际的更好融合,需要更多建立在理论基础上的针对现行教材的教学设计和实践.
二、APOS理论指导下 “锐角三角比的意义”教学设计
“锐角三角比”承接着中学阶段平面几何和函数这两大体系中的重点问题——“相似三角形”和“三角函数”,同时它又是“图形函数问题”和“函数图形问题”的重要载体,数形结合的典范,故历来是初三阶段学习、考核的重点和难点.
在上海市教材中“锐角三角比的意义”大纲安排为2课时,作者立足于教材,结合APOS理论进行教学设计,以下是截取的部分教学片断及说明:
教学片断1:通过“行动”引入概念.
问题1:在图1~3中,能否确定未知边、角的值?怎样求?
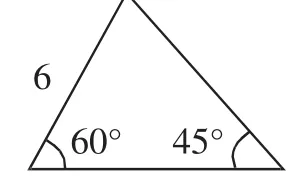
图1
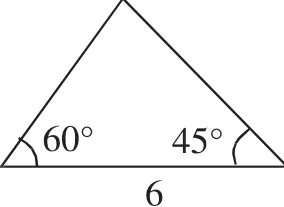
图2
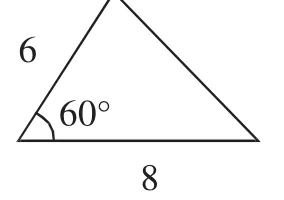
图3
问题2:(1)若把上题中的特殊角改成一般角呢?如图4~6,未知边、角的值是否也唯一确定?

图4
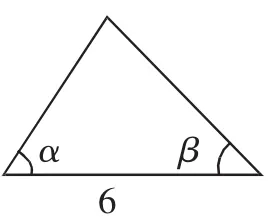
图5
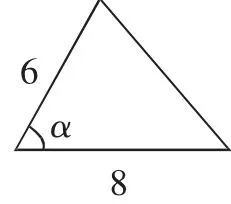
图6
(2)如图7,构造Rt△ABD和Rt△ADC.
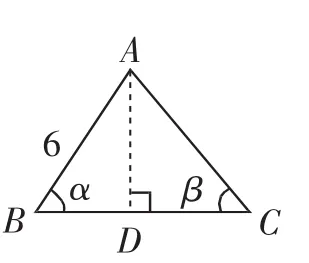
图7
在让学生充分地自主思考和交流后,教师因势利导,利用直角三角形给出锐角三角比的定义.
设计意图:在教学实践中我们常常发现有的学生虽能熟背概念却不能用其解题,怎样才能使概念教学更好地为解题服务呢?本设计从概念的引入出发做了一些尝试.根据APOS理论,“行动”是概念学习的第一阶段,通过操作让学生体会概念产生的背景和意义将有助于加深概念的理解,并从本质上提高概念的应用能力.设计中的问题1和问题2围绕概念的应用展开,同时又基于学生们熟悉的全等三角形和特殊角的直角三角形问题,合理的“脚手架”设置让学生得以在一步一步的“行动”中发现问题的突破口,不仅使概念的给出显得水到渠成,且为如何应用概念解决问题指明了方向.
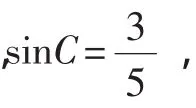
总结归纳:如图8,已知∠A的正弦(余弦、正切、余切)值,请同学们填空并总结公式a=______=______;c=________=_______;b=_______=________.
教学片断3:反复操作实现内化.练习:
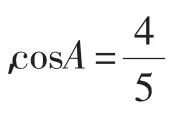
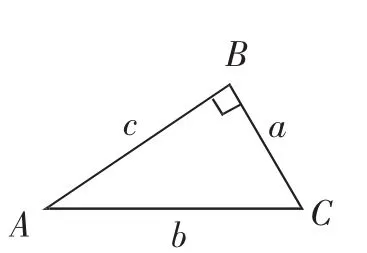
图8
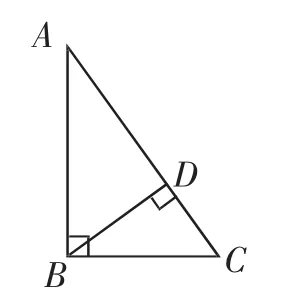
图9
设计意图:如何帮助学生在了解概念的基础上更快、更全面地熟悉概念并用于解题?APOS理论认为反复操作是实现“行动的内化”(interiorization)的必要过程,因而此时引入一定数量的变式训练恰逢其时.由于“行动”已渐渐为个体所熟悉并形成“程序”,给出的例题和练习亦须符合相应的心理特征才能达到最佳的教学效果.例1依托于锐角三角比基本概念,此时出现具有双重作用:首先,其解决过程需要对概念的反向操作,即“程序的逆转”,而这正是APOS理论中“程序”阶段的心理特征之一,同时,例1的结论是之后解决三角形问题的基础,相应的总结及巩固练习有助于学生概念应用能力的提高.
教学片断4:程序的压缩与解压缩.
思考并小结:同一个角的正切值和余切值有什么关系?正弦值和余弦值呢?
教学片断5:针对“对象”的性质讨论.
例3 已知:0°<∠A<∠B<90°,则sinA_____sinB;cosA____cosB;tanA____tanB;cotA______cotB.
设计意图:我们都知道提高解题能力的诀窍之一是把某些复杂的“程序”“压缩”(encapsulation)为“对象”.APOS理论认为实现“压缩”不仅需要个体主动、反复运用“程序”去实施相应的行动,解压缩(de-encapsulate)的过程同样十分重要.例2的解决需要反复实施“压缩”和“解压缩”的过程,它的操作有助于锐角三角比作为一个工具的形成.而一旦锐角三角比脱离了直角三角形作为独立的“对象”出现,对其相关性质的讨论可以让学生从不同角度审视它,从而更深刻地理解它.在利用例2、例3得出结论的过程中,教师要引导学生主动探索并引起讨论,最后通过总结帮助学生完成从感性认识到抽象概括的升华.
教学片断6:程序的组合,纳入知识体系,形成图式.
思考题:1.sinα是方程3x2-7x+2=0的一个根,求tanα.
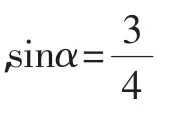
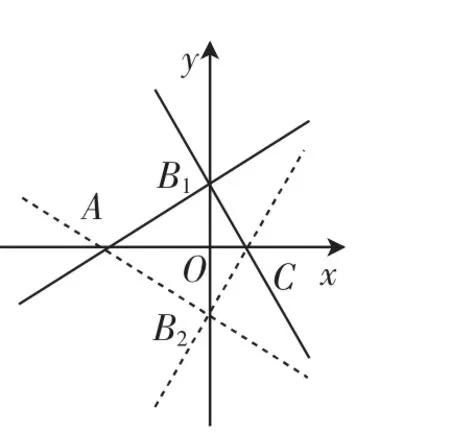
图10
设计意图:锐角三角比工具可以帮助我们解决大量函数、图形等综合性问题,但实现的前提是能进行程序的组合并把新的概念纳入原有知识体系.APOS理论指出,概念需要在循环的过程中才能逐步纳入已有的知识体系,形成心理图式(见APOS理论模型图,如图11).题1不仅把锐角三角比与一元二次方程结合,而且需要考虑到其作为对象的多种性质(取值范围等);题2则更是把概念直接纳入了函数问题中,且需要考虑两种不同的情况,问题本身不难,却集中了几何和函数的双重背景,为将来函数图像题和图像函数题的解决打下伏笔.
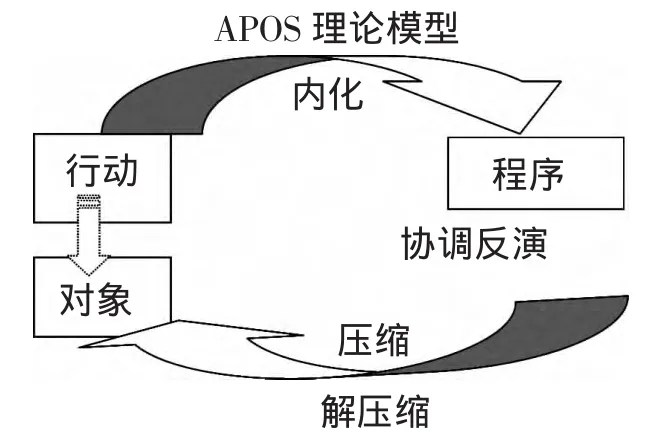
图11
三、APOS理论指导下概念教学的几点建议
(1)在学习之初,通过“行动”帮助学生了解概念产生的意义和应用价值是APOS理论指导下概念教学的重要一环,而选择好的问题让学生操作则是成功的关键.同时,所谓“过犹不及”,好的问题也要结合时间和进程的合理控制,以保证后阶段学习的顺利进行.
(2)APOS理论给我们最重要的启发之一便是概念教学必须遵循一定的心理学规律.忽视对学生学情的了解,一味贪多求难,只能“欲速则不达”,而循序渐进的教学设计才是最有利于学生牢固掌握知识和提高解题能力.
(3)图式的形成是一个渐进的建构过程,要实现这一过程、对象阶段的反复压缩、解压缩必不可少,好的例题能使练习更高效,从这一角度,传统教学中的变式训练在概念教学的某些阶段具有其独特的价值,理应得到合理继承和发扬.
1.鲍建生,周超.数学学习的心理基础和过程[M].上海:上海教育出版社,2009.
2.上海市中小学(幼儿园)课程改革委员会.九年制义务教育课本·数学·九年级第一学期[M].上海:上海教育出版社,2007.
