浅谈推理在初中数学教学中的实施策略与实践

☉江苏省如东县实验中学 陈春梅

一、问题的提出

波利亚曾说：“数学问题的发现与创造在于推理.”爱因斯坦也在回顾自己发现质量守恒定律时，谈及中学时代的学习收获：“我经常用类比推理的方式去想一个问题，觉得发现一个问题比解决一个问题更重要.”从大师们的言语中，我们可以收获这样的认识：推理是培养一个学生思维发散性、严密性的良好方式，也是激发学生学习兴趣的重要手段.

根据诸多研究资料显示，初中生推理能力的增长相比学生学习的数学知识而言显得太落后、太缓慢了.初中生的理性认知能力远远低于感性认知水平，推理便是培养理性思维的一个良好的武器，随着初中数学新的知识增多，而且问题的形式也是千变万化，推理能力若得不到有效的提升，极易造成他们只会就题论题，而不会对知识有一个融会贯通.因此，本文就如何培养学生在推理能力上做了一番实践和思考，不当之处请读者补充指正.

二、界定和意义

首先，谈谈推理的界定：推理是波利亚首先提出的，他认为个人会依据存在的事实和已经获得的正确结论为前提（包括各种各样的经验和外部成果），以及个人的直觉猜测未知问题的一种模式.新课标对推理能力有这样的要求：即通过主动学习、实践发展学生的推理能力，并有助于通过推理培养学生的创新能力和意识.

其次，浅要分析推理的意义：众所周知数学问题是千变万化的，有些是解题的多变化，有些是从一维上升到二维平面的思维转变，有些则是从问题中提炼出数学思想方法的提升等，只要对学生进行有效的引导，就能不断培养学生在数学学习过程中使用推理的意识.因此初中数学教学需要推理，就像黑暗中的一盏明灯，它培养的不仅仅是数学推理方面的能力和成绩，将来也会给学生的生活、工作带来积极的效应，因此，培养学生推理能力的教学必须予以重视，要从多方面的角度进行多元化的尝试.

三、实践与策略

1.策略一——课堂教学中推理能力的渗透

旧版教材对学生的要求更注重知识的传递，数学形式化结果的证明、理解和掌握，往往忽视学科之间的联系性，淡化了其他学科诸人文、历史等对数学学习的作用，因此新课程顺势而为，更注重了知识形成的过程，淡化了形式化结果的证明，强调从感性到理性的推理成为主流（对初中生而言极为合适），课堂教学中如何进行推理能力的渗透和培养呢？笔者以数学史为例，近年来数学文化、数学美渗透到数学课堂中去呈现出一种上升的趋势，但受应试等多方面因素制约，其运用并不广泛.其实，数学也有很多脍炙人口的轶事，有时不妨拿来一用，也可以取得意想不到的效果.

案例1 苏教版初中数学八年级下第七章7.1《生活中的不等式》.

本课是不等式一章中的第一课时，主要通过本节课的学习让学生感受不等关系的存在与应用.通过学生自主学习，以便培养学生更深层次地从理性角度建立不等观念的尝试.

（1）创设情境.

自然层面引入：“横看成岭侧成峰，远近高低各不同”.人文层面引入：两个身高测量值均为178cm的人，他们身高是否真的完全一样呢？

历史层面引入：在古代，我们的祖先已经懂得使用杠杆原理，并根据这一原理设计出了一些简单机械，把它们用在生活实践中.

（2）建构过程.

教师编制一个不等式，然后请同学们自己模仿编一个不等式的问题，用以推理不等关系.

师：2011年3月，日本本州岛附近海域发生强震，现在对强震遗留下来的什么最担心？核危机！核辐射主要存在三种射线：Alpha（阿尔法）射线、Beta（贝塔）射线、Gamma（伽玛）射线.我们不妨记Alpha（阿尔法）粒子的质量为a，Beta（贝塔）粒子的质量为b，Gamma（伽玛）粒子的质量为c，三者的质量关系是a＞b、b＞c，那么：如果把前两种粒子放在天平上，由于a＞b，显然左端会下降；若我们将其交换位置，则右端会下降，于是我们得到：若a＞b，则b＜a.

生：我这样认为，由于三种粒子的的质量关系是a＞b、b＞c，得到a＞c.（传递性）

说明：在这样的背景下实施自主建构教学，既针对性地解决了学生主动推理解决问题，又改变了学生被动接受学习的坏毛病，久而久之，势必给自主建构结合主动推理的教学方式渗透进课堂，以及给学生感受数学知识的运用，提升数学素养带来极大的帮助.

2.策略二——解题教学中推理能力的培养

根据一些文献研究，变式教学作为我国数学教学的优良传统，在学生推理能力的培养上起着开发作用.中考数学依旧是以解题为主教学的最终体现，如何高效实施解题教学并从中提高学生推理问题的能力，这正是变式教学所能体现的（很多教师并没有关注变式教学对推理能力的培养）.因此笔者认为，变式教学模式是提高推理思维深度和广度的较好方式.

案例2距离最小问题解题教学.

（1）问题基本原理.

已知，点M，N在直线AB的异侧，在AB上找一点，使点P到点M，N的距离和最小.

解决方法：如图1所示，利用三角形两边之和大于第三边可知，三点共线时距离和最小.

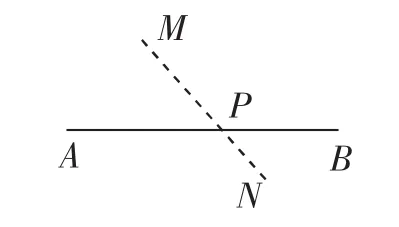
图1

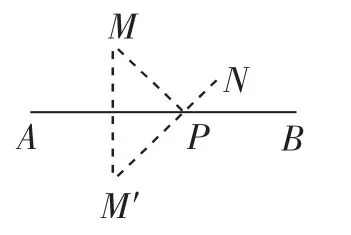
图2

（2）变式基本原理.

已知，点M，N在直线AB的同侧，在AB找一点P，使P点到点M，N的距离和最小.

解决方法：将同侧点问题转化为异测点问题，作M关于直线AB的对称点，问题转化为教材基本模型.

（3）变式推理教学.

一个长方体形的木柜放在墙角处（与墙面和地面均没有缝隙），有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.①请你画出蚂蚁能够最快到达目的地的可能路径；②当AB=4，BC=4，CC1=5时，求蚂蚁爬过的最短路径的长；③求点B1到最短路径的距离.

解决方法：①木柜的可见表面展开图是两个矩形ABC′1D1和ACC1A1.蚂蚁能够最快到达目的地的可能路径有A1C′1和AC1.

②蚂蚁沿着木柜表面经线段A1B1到C1，爬过的路径的长， 蚂蚁沿着木柜表面经线段BB1到C1，爬过的路径的长是最短路径的长是l2=

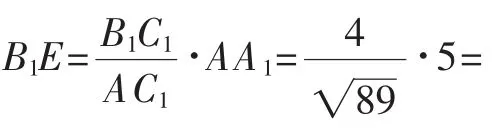
说明：本题以实际应用型问题为背景，将距离和最值隐藏于问题的情境之中.其变式的角度在于，问题情境的变化，要求学生以基本模型知识为保障，推理分析最值可能产生的前提下，将距离最小问题转化为两边之和的最小值问题.

四、推理的思考

以上是笔者亲历推理教学的一点实践，总结上述推理在初中数学中的运用，笔者有以下一些不成熟的思考，和大家交流：

（1）推理的经验性.由推理的概念，我们可以知道推理来自于个体的已知知识范畴，那么个体的经验就显得极为重要，个体经验较多则推理的准确度越高，反之则较低.

（2）推理的创新性.正因为有着自由性，因此学生对推理的结果也会百花齐放，在推理上会出现各种各样创新式的结论，这也和新课程努力培养学生的创新思维的理念密切相关.

（3）推理的主动性.本文以初中数学教学最常见的两种策略，即课堂教学培养策略和解体教学培养策略出发，均以学生积极主动参与为背景设计教学，将推理能力的培养始终蕴藏在主动建构的环境中.

总之，推理不是仅限于合情推理和演绎推理，也可以从初中数学教学的两个常规方面进行挖掘.本文突破了传统推理仅限于数学中所讲的合情推理和演绎推理的限制，更是从数学问题的背景分析中进行推理能力的培养，因此教师努力在课堂教学中渗透推理的思想、在解题教学中冠以推理的尝试、在课后的数学探究中多多进行推理的合作，通过全方位、多元化的手段对学生进行推理能力的熏陶，那么笔者认为：我们不仅仅教会了学生数学的基本知识和基本技能，也提高了学生用已知知识去应对未知问题的能力，这不正是和新课程理念殊途同归吗？

1.全日制义务教育数学课程标准解读［M］.北京：北京师范大学出版社，2002.

2.［美］G.波利亚.怎样解题——数学教学法的新面貌［M］.上海：上海科技教育出版社，2002.

3.渠东剑.探究方法比探究结果更重要［J］.中学数学教学参考（中），2013（4）.

4.倪兴隆.一题多解，提高学生思维与逻辑推理能力［J］.中学数学（下），2012（12）.