超声波检测中波型转换的计算分析

孙朝明

（中国工程物理研究院机械制造工艺研究所，绵阳 621900）

利用数值模拟或仿真方法，可深入了解超声检测过程中超声波的传播特性及其与工件的相互作用，有针对性的进行检测参数设置与优化，有助于理解检测结果。国外推出了较成熟的超声检测仿真软件，如CIVA，i mage3 D等，国内相关研究机构在超声检测声场计算分析方面也进行了相应的研究[1－3]。在超声检测仿真技术中，声线跟踪方法具有简单明了的优点，可直观显示超声波的传播路径及覆盖范围，得到超声回波的位置，但在描述回波信号的强弱方面存在不足[4]。其主要原因在于两个方面，其一是声线跟踪时未考虑波型的转换，没有计算在传播过程中产生的全部反射、折射声线；其二是声线跟踪时仅计算传播路径及时间，而未对每条声线对应的声压值及其变化情况进行计算[5]。在声线跟踪时，不计算超声信号幅值的变化，显然很大程度上影响到其实用价值[6]。

对于超声波而言，随着声波类型的不同、界面两侧物质的不同、声波入射角度的不同，所产生的反射[7]或折射情况及对应声压变化存在明显差别。将此差别考虑进来，有望解决声线跟踪方法中回波信号强弱描述方面的不足；同时，通过计算每一声线的传播情况及对应的声压值，可在声线跟踪时对声压值很低的声线中止跟踪计算，从而节约计算开支。

1 理论与方法

1.1 Snell定律

当一束超声波到达两种材料的界面时，会出现下面两种情况：一是超声波会像光波一样发生折射；二是在界面处发生波型转换，如图1所示。

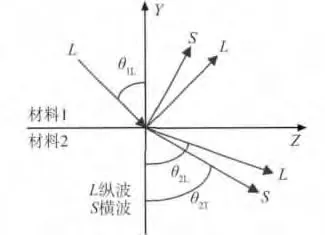
图1 界面上的波型转换

利用球面波传播的Huygens（惠更斯）原理，可推导出两材料界面两侧的Snell定律表达式[8]：

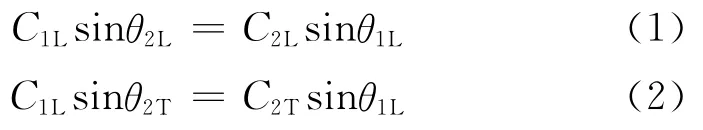
式中：C1L，C2L，C2T分别为超声在材料1中的纵波声速，在材料2中的纵波声速，在材料2中的横波声速；θ1L，θ2L，θ2T为纵波入射角，纵波折射角，横波折射角。

1.2 超声振幅变化分析

在两种不同物质界面处的反射与折射问题是应力波传播研究中的最重要问题之一，相应声波的振幅在反射或折射后发生变化，变化后的振幅与原来的振幅之比即为反射系数或折射系数。

不失一般性，入射纵波在两种材料均为固体的界面处可能产生反射的纵波、横波与折射的纵波、横波。

图1中，在y＝0处满足质点速度连续条件[8]：

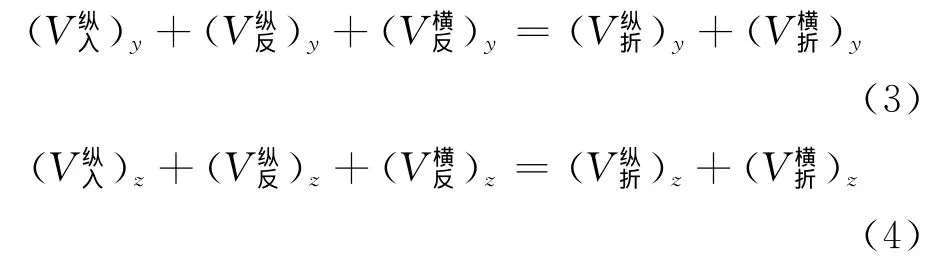
在y＝0处满足应力连续条件：

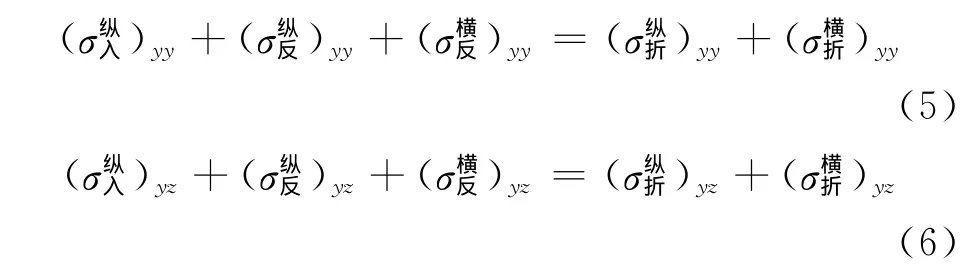
式中：符号右侧上方文字表明声波的类型为纵波或横波，下方文字为声波的作用方式入射、反射或折射，括号下方字母表明在此方向的分量。后文中符号的表示及含义相同。

考虑声波为简谐运动，利用速度位移关系、应变位移关系、应力应变关系对式3，4，5，6进行组合，可得到如下公式：

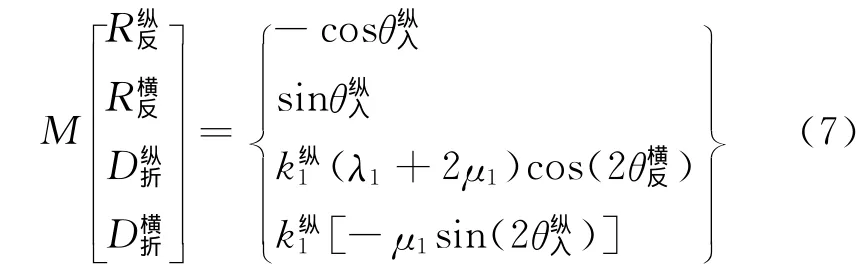
式中：M为与反射角、折射角、两种材料拉梅常数相关的4×4矩阵，拉梅常数即公式右侧的λ和μ，k为波矢ω/c。

对于入射横波，需将式7的右侧进行相应变化。对于固液、液固界面而言，也可直接使用式7进行计算，但需考虑液体中不能传播横波。

超声波入射到铝、有机玻璃界面时，按式7进行计算可得到相应的反射与折射系数如图2所示，其中横坐标为入射角度，纵坐标为波幅变化系数。在纵波入射角度接近0°时，反射横波与折射横波的振幅很小，在后续的与工件作用过程中很快衰减。在横波入射时，根据Snell定律，在入射角接近30°时，反射纵波消失。

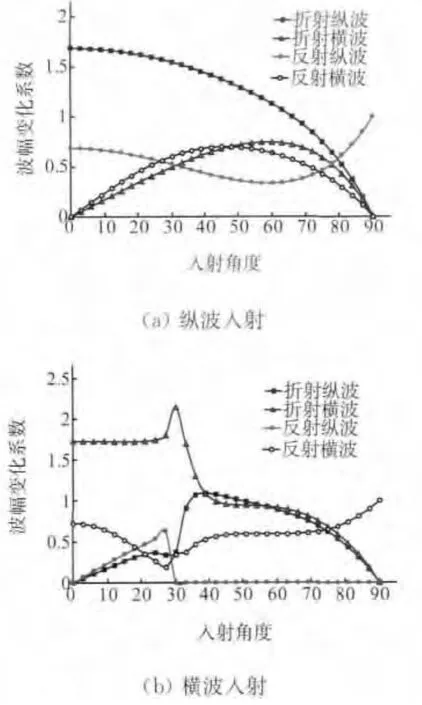
图2 超声波入射到铝－有机玻璃界面的反射、折射系数

2 数值模拟

利用自行开发的超声声线仿真软件，进行了超声检测仿真试验。检测工件为11.8 mm厚钢板，探头为直探头5P14，频率为5 MHz，检测时利用水浸法，探头距离钢板上表面为24 mm。

利用Snell定律可计算出超声在入射界面处的波型转换情况，如果相应的角度大于90°则对应的波型不存在。如果声线跟踪结束时，未能返回探头，则不显示对应的声线。利用声线跟踪方法得到的图形如图3所示，对应的声线跟踪次数为6。可以直观看出，超声从水中折射到钢板、在钢板中反射、从钢板折射到水中的情况。

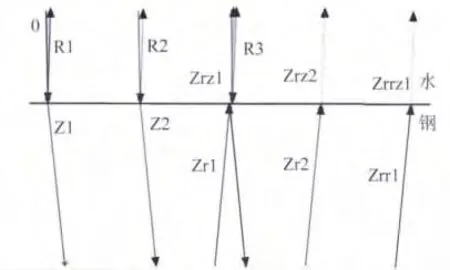
图3 水浸法检测钢板

超声波在钢上表面与探头间进行3次反射，分别如R1－R3所示。超声第1次折射到钢中，记作Z1，之后在钢表面反射为Zr1，再折射到水中为Zrz1；超声第2次进入钢中的情况相类似。

如果查看回波信号，并对其返回探头的时间进行统计，可得到图4的结果，其中横坐标为超声传播时间（微秒），纵坐标为统计次数。由于没有考虑回波信号在振幅方面的差别，均视为相同的振幅，因此得到的回波情况与实际存在较大出入。需要说明的是，从钢中折射到水中的Zrz1又在探头和钢板表面进行反射，信号Zrzr1又回到探头。因此，信号在68.9μs时与Zrz2有所叠加，此刻的回波出现2次。

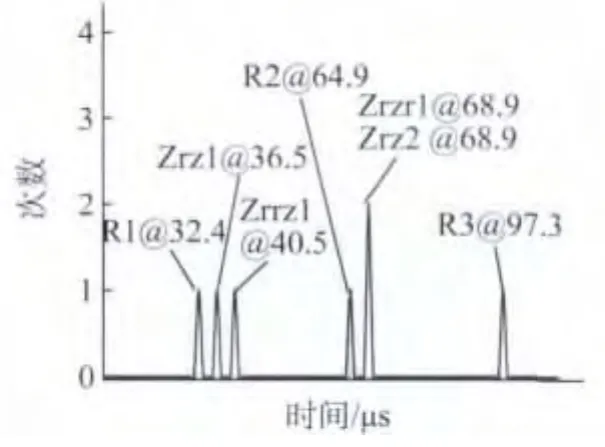
图4 探头接收的回波信号数量统计

根据前述的超声振幅变化分析公式，可对超声声束在界面发生的反射、折射率进行计算，结果如图5所示。

图5 纵波在水钢界面的反射与折射系数

为真实反映对应的检测回波信号，在探头主声束的辐射场内构造100条声线，每条声线的初始振幅设定为100，当振幅小于0.4时终止声线跟踪，跟踪次数限为40次。探头直径为14 mm，其表面的保护材料视为有机玻璃。经数值模拟计算后的回波信号振幅如图6所示。与图4相比较，图6所得到的结果更能真实反映出检测中信号的幅值变化情况。

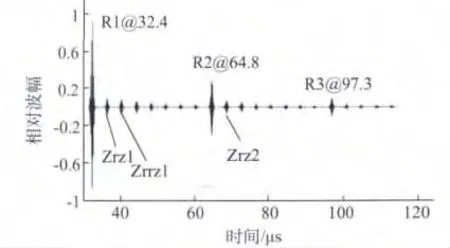
图6 探头接收的回波信号振幅分析

3 试验

利用水浸方法进行了实际检测试验。使用探头为汕头超声电子的直探头5P14（频率为5 MHz），使用的超声探伤仪为GE公司的USN60，检测对象为100 mm×100 mm×11.8 mm的钢板。试验时将钢板浸入水槽中，将超声探头固定于支架上并与钢板平面垂直，调节探头与钢板的间距为24 mm。

探头接收到的回波信号如图7所示。图中显示范围为250 mm，在钢界面回波R1和R2间可以明显看出7个回波峰，对应于声波第一次折射入钢板内，然后分别在钢板内经1－7次反射后从钢折射到水中返回探头的信号。与图6相对照，可以看出试验结果与数值模拟结果基本一致。

图7 探头接收的回波信号

在图6中的第一个回波峰幅值Zrz1最高，然后依次降低；而在图7中，第二个回波峰Zrrz1幅值最高，之后依次降低。分析其原因，主要是探头与钢板的距离相对较近，检测时在探头的近场区内，而近场区内的声压分布不均。在试验中，水层厚度较小，近场区分布在水、钢两种介质中。通过计算可知，探头在均匀介质钢中的近场长度为41.5 mm，而对应于水钢两种介质，水层厚度为24 mm，在钢中的剩余近场区长度为35.2 mm。因此，回波信号Zrz1处于近场区内，其余的回波信号则不在近场区。

以钢界面回波R1的幅值作为参考，分别将R1到R2间的8个回波峰值调节到仪器的满刻度，并记录对应的分贝值。将这些值分别减去回波R1满刻度时的分贝值，可以得到各回波幅值的相对衰减量。结果如图8所示。钢界面的二次回波R2与一次回波R1相比，对应的试验及模拟结果的幅值变化量差别较少。其间的回波与钢界面一次回波R1相比，对应的变化趋势一致，偏差值约为5 dB。

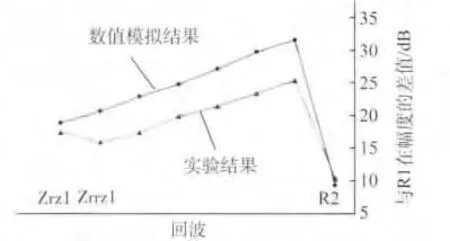
图8 回波信号的幅值变化量

4 结语

分析了超声波在界面上的波型转换及反射波、折射波幅值变化的计算方法，在此基础上对超声声线跟踪方法进行完善，对回波信号的产生规律及幅值特征进行了数值计算。结果表明：

（1）对超声波波型转换规律及幅值特征的计算，可解决传统声线跟踪方法不能描述回波信号幅值变化的难题，计算的回波信号特征基本上与试验结果一致，幅值变化量的计算偏差值约5 dB。

（2）波型转换的分析计算可完善声线仿真方法，不仅可对声波的传播路径、时间进行定量，还可得到接近真实的回波信号，为特定条件下超声检测问题的深入计算分析，奠定了技术基础。

[1]丁辉，张俊，张益成，等.超声检测声场计算模型的建立与仿真软件的开发[J].无损检测，2009，31（8）：614－618.

[2]陆唯一，张琦，阙沛文.石油管道检测中超声探头的选择及声场分析[J].传感器与微系统，2007，26（8）：20－25.

[3]韩鹏，王召巴，陈友兴.多元高斯声束模型相控阵超声传感器声场仿真[J].传感器与微系统，2010，29（2）：22－25.

[4]张伟志，刚铁，王军.超声波检测计算机模拟和仿真的研究及应用现状[J].应用声学，2003，22（3）：39－44.

[5]SCH MITZ V，WALTE F，CHAKHLOV S V.3D ray tracing in austenite materials[J].NDT＆E Inter national，1999（32）：201－213.

[6]KOLKOORI S R，RAH MAN MU，CHINTA P K，et al.Ultrasonic field profile evaluation in acoustically inho mogeneous anisotropic materials using 2D ray tracing model：Nu merical and experimental comparison[J].Ultrasonics，2013（53）：396－411.

[7]彭通，徐平.纵波反射系数影响因素分析[J].现代矿业，2009（484）：67－70.

[8]J.L.罗斯.固体中的超声波[M].何存富，等，译.北京：科学出版社，2004.