基于有限元仿真和数据拟合的管道缺陷量化分析方法

2014-07-23张峻峰王宏阳马瑞泽

无损检测 2014年2期

冯健，张峻峰，王宏阳，马瑞泽

（东北大学信息科学与工程学院，沈阳 110819）

管道作为现行的五大运输工具之一，运量大、占地少、安全可靠、投资成本低，其在运送气体、液体等方面的优势不容小觑。随着管线的增多，管龄的增长，腐蚀泄漏事故频繁发生，造成了严重的资源浪费和环境污染问题，管道检测技术的研究逐渐受到重视。

管道检测是为了保证管道的安全可靠性而发展起来的一项技术，其目的是能真实地检测出管道缺陷的位置、损伤程度和缺陷尺寸[1－2]。当前管道内检测技术使用较多的是漏磁检测和超声波检测技术。与超声波检测技术相比，漏磁检测技术的优点如下：检测速度快，对管道输送的介质不敏感，对于内部缺陷拥有较高的灵敏度[3]。

管道漏磁检测的关键环节是建立反映相应静磁现象的数学模型，确定缺陷尺寸与漏磁信号特征值间的关系，实现对缺陷参数的定量识别。为此，笔者利用ANSYS有限元分析软件建立了管道漏磁内检测的二维实体模型，对不同长度和深度的管壁内部缺陷进行了漏磁检测仿真，获得了管壁缺陷的漏磁场信息。运用最小二乘数据拟合方法对缺陷的参数进行了量化研究。

1 缺陷漏磁场数学模型

首先对钢质管道作如下假设：管材的磁性质是均匀、各向同性的，即管道内部各点的材料磁导率μ相同，空间不同方向的导磁率相同。根据管道轴对称的结构特点，将分析确定为二维静磁场分析，其Max well方程组为：

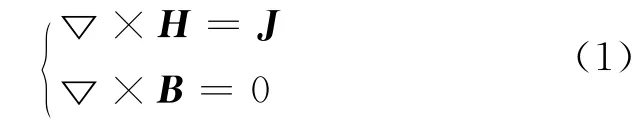
式中：H为磁场强度矢量；B为磁通密度矢量；J为等效电流密度；μ为材料的磁导率。

由于磁场的无源性，引入矢量磁势A，使：

由上面各式可以得到：

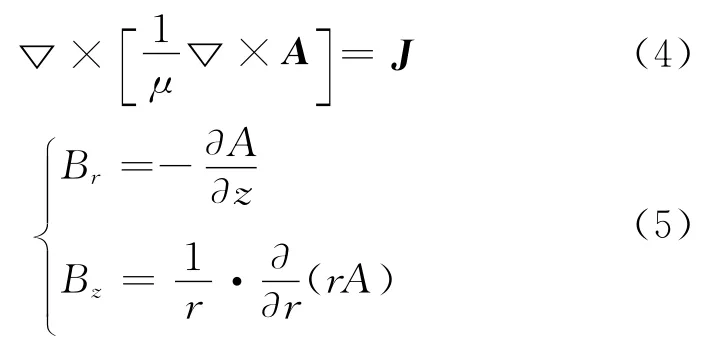
对几何结构对称的管道磁场，采用圆柱坐标系（r，θ，z），A＝A（r，z）e0，其中，e0是H 方向的单位矢量，则方程（4）可化简为：

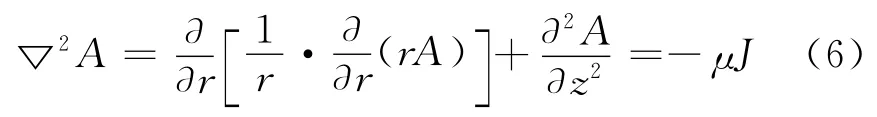
矢量磁位方程（6）满足泊松方程，属于泛定方程，将它与边界条件结合起来，构成了边值问题，它是待求问题的数学模型。对轴对称圆柱坐标系统的管道来说，矢量磁位的边界条件可写为：

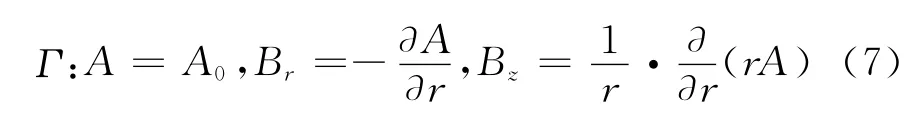
应用解析法对上面的数学模型进行求解很困难，通过建立一个与式（6）等价的能量泛函，并在一近似的函数空间内求此泛函的极小值，且相应的边界条件为Γ，可以求得此几何结构对称的管道漏磁场有限元模型的解和空间中任一点的磁力线分布与磁场强度值。

2 管道漏磁内检测有限元仿真

根据漏磁检测装置测量部分的实际形状建立的实体模型如图1所示。两磁极间距离为0.28 m；缺陷为长20 mm，管壁深40%的内部缺陷；管壁厚度为0.012 m，长为0.46 m；磁铁长0.08 m，厚0.03 m；钢刷长0.08 m，厚0.05 m；衬铁长0.36 m，厚0.02 m；管壁外取0.05 m宽的空气区域。

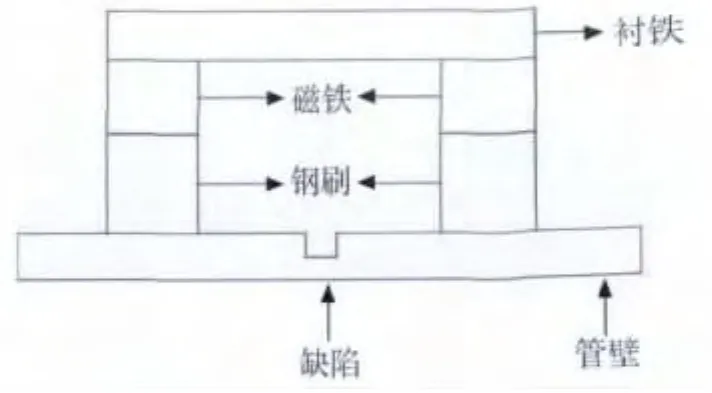
图1 漏磁检测装置实体模型

在模型中需要定义的材料有：空气、磁铁、衬铁、钢刷、被测管壁。定义空气的相对磁导率为1；磁铁设置为线性材料[4]，相对磁导率为1.083，矫顽力设置为955 000 A/m；管壁选用X52号钢；衬铁设置为线性材料，相对磁导率为300；钢刷采用与衬铁相同的材料。

给模型划分网格之前需要给各部分区域定义单元类型、材料特性和单元坐标系。在模型中定义的单元类型为PLANE53，设定属性为轴对称。因模型属于二维模型，而且自由度的数目较少，故采用直接求解器[5－6]。

求解结束后，ANSYS的后处理器提供的二维磁力线图可以清楚、直观地表现出管壁缺陷处磁场的空间分布情况，如图2所示。

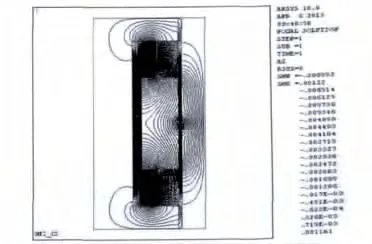
图2 仿真模型磁感应线分布

3 缺陷外形尺寸与漏磁信号的关系研究

3.1 缺陷长度与漏磁信号的关系

缺陷深度一定（20%）时，模拟得到的不同长度缺陷的磁通密度轴向分量和径向分量曲线如图3。

取每条曲线上纵坐标值大于此阈值的点中横坐标最大和最小的两点的横坐标差值为阈值跨度[7－8]。从图3（a）中可以看出，如果缺陷的深度一定，磁通密度轴向分量的阈值跨度随着缺陷长度的增大而变大，因此磁通密度轴向分量的阈值跨度与缺陷长度存在一定关系[9]。从图3（b）中可以看出，如果缺陷的深度一定，磁通密度径向分量峰间距随着缺陷长度的加长而变大，因而磁通密度径向分量峰间距与缺陷长度存在一定的关系[10]。

图3 不同长度缺陷的漏磁通密度的分量曲线

3.2 缺陷深度与漏磁信号的关系

缺陷长度一定（20 mm）时，模拟磁通密度随缺陷深度的变化，得到不同深度缺陷的磁通密度轴向分量及径向分量曲线如图4所示。

从图4（a）中可以看出，如果缺陷长度一定，磁通密度轴向分量幅值随着缺陷深度的加深而变大，因而磁通密度轴向分量峰值与缺陷深度存在一定的关系。从图4（b）中可以看出，如果缺陷长度一定，磁通密度径向分量幅值随缺陷深度的加深而变大[11－12]，因而磁通密度径向分量峰－峰值与缺陷深度存在一定的关系。

4 管道缺陷量化分析

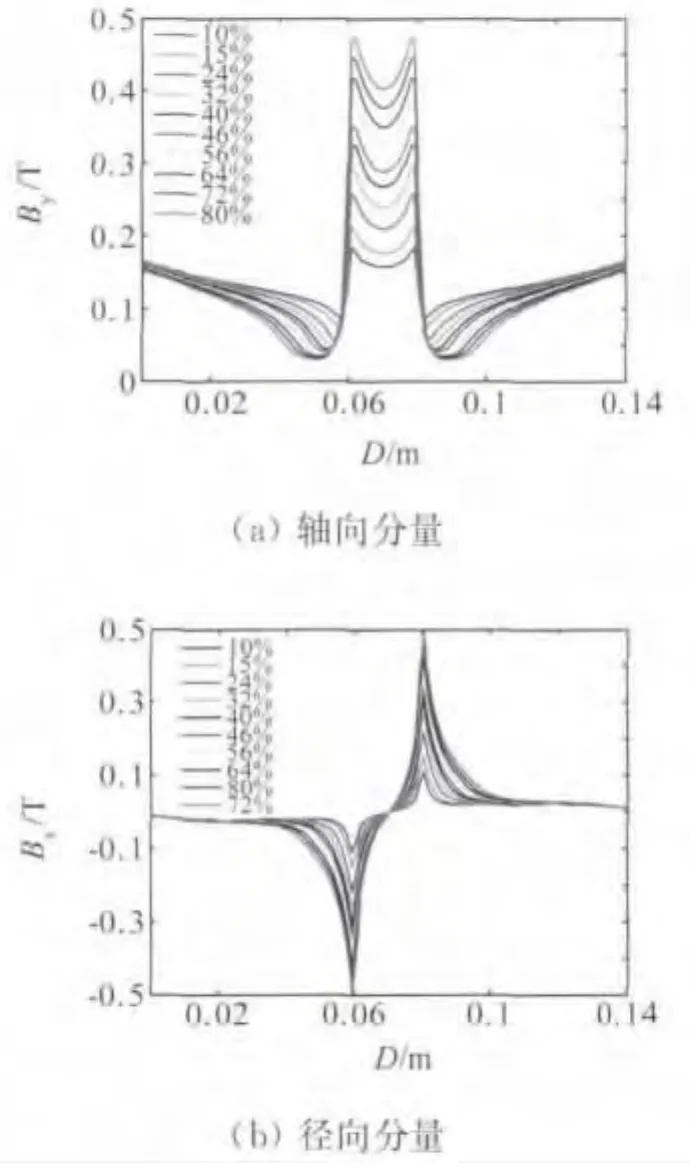
图4 不同深度缺陷的漏磁通密度的分量曲线

通过以上分析可知，磁通密度轴向分量特征值为峰值及阈值跨度，磁通密度径向分量特征值为峰峰值及峰间距。当缺陷尺寸改变时，这四个特征值随之变化，满足一定的函数关系。为确定缺陷尺寸与四个特征值对应函数关系，利用ANSYS有限元分析软件进行仿真。设置的缺陷参数为：取定深度为20%，在5～100 mm之间取40组不同长度值；取定长度为20 mm时，在10%～80%之间取40组不同深度值，共得到80组数据，为拟合函数关系式提供了必要的数据[13－14]。

分析可知，缺陷的长度和深度与磁通密度的两个分量之间存在一定的关系，首先研究缺陷的长度和深度与磁通密度某一个分量之间的定量关系[15]。

缺陷长度与磁通密度轴向分量阈值跨度之间近似为线性关系，拟合曲线方程为：

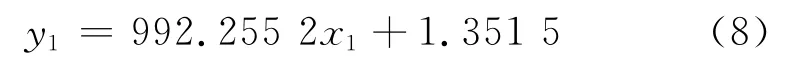
缺陷长度与磁通密度径向分量峰间距之间近似为线性关系，拟合曲线方程为：

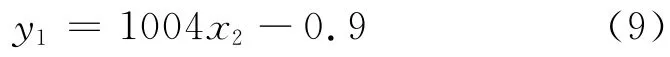
式中：y1为缺陷长度；x1为磁通密度轴向分量阈值跨度；x2为磁通密度径向分量峰间距。

缺陷深度与磁通密度轴向分量峰值之间近似为线性关系，拟合曲线方程为：

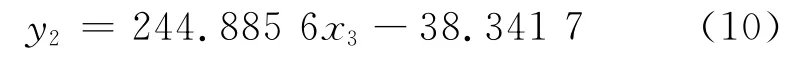
缺陷深度与磁通密度径向分量峰－峰值之间近似为线性关系，拟合曲线方程为：

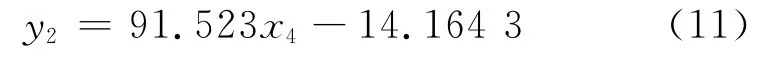
式中：y2为缺陷深度；x3为磁通密度轴向分量峰值；x4为磁通密度径向分量峰峰值。

由于单独使用一个分量对缺陷特征的量化精度可能会偏低，下面对缺陷的长度和深度分别进行基于两个分量的一次拟合和二次拟合，判断拟合结果的量化精度是否优于单独使用一个分量进行量化的情况[16]。

由于缺陷长度与磁通密度径向分量峰间距和轴向分量阈值跨度有关，将上述两个分量进行一次拟合，得到缺陷长度量化一次拟合方程：

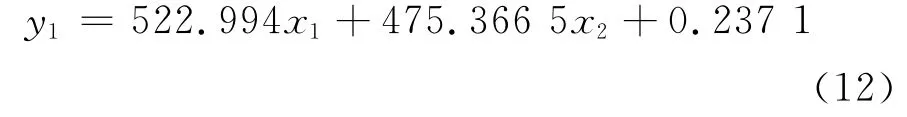
将磁通密度径向分量峰间距和轴向分量阈值跨度进行二次拟合，得到缺陷长度量化二次拟合方程：

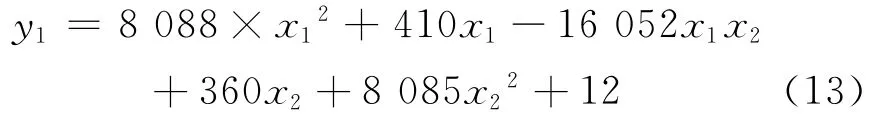
式中：变量含义与单变量拟合时相同。

缺陷深度与磁通密度径向分量峰－峰值和轴向分量峰值有关，将上述两个分量进行一次拟合[17－18]，得到缺陷深度量化一次拟合方程：

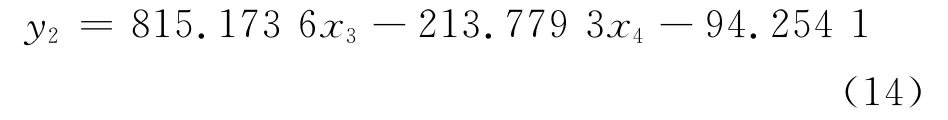
将磁通密度径向分量峰－峰值和轴向分量峰值进行二次拟合，得到缺陷深度量化二次拟合方程：

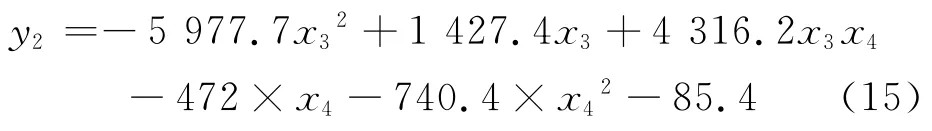
式中：变量含义与单变量拟合时相同。

5 结果与讨论

5.1 仿真结果误差分析

定义长度在0.1～5 mm范围内的缺陷为小长度缺陷，在5～100 mm范围内的缺陷为中长度缺陷，在100～130范围内的缺陷为大长度缺陷。在上述三种长度区间范围内分别抽取5组数据进行误差分析。定义深度在1%～10%范围内的缺陷为小深度缺陷，在10%～80%范围内的缺陷为中深度缺陷，在80%～100%范围内的缺陷为大深度缺陷。在上述三种深度区间范围内分别抽取5组数据带入以上所得量化方程进行误差分析。

综合单独利用某一轴向的数据进行量化以及将两个轴向的数据进行拟合再进行判定的误差分析结果，笔者所述四种拟合方程对各类缺陷的适用情况如表1所示。

由表1可得，对于中长度缺陷，采用轴向一次拟合方法量化精度最高；对于大长度缺陷，采用轴向径向一次拟合方程量化精度最高；对于中深度及大深度缺陷，均为采用轴向径向二次拟合方法量化精度最高；对于小长度及小深度缺陷，所述四种拟合方法均不能做出有效的量化，这可能是因为小长度及小深度缺陷漏磁信号较弱，不同长度、深度的缺陷信号差别不明显，难于识别。

表1 四种拟合方程对各类缺陷的适用情况

5.2 实际案例研究

对一个内表面存在缺陷的实体管道进行磁感应强度测试。缺陷的直径为20 mm，深度为8 mm（75%），如图5所示。

图5 存在缺陷的实体管道

利用前文所述缺陷量化方法，对缺陷特征值进行量化与误差分析，结果如表2所示。

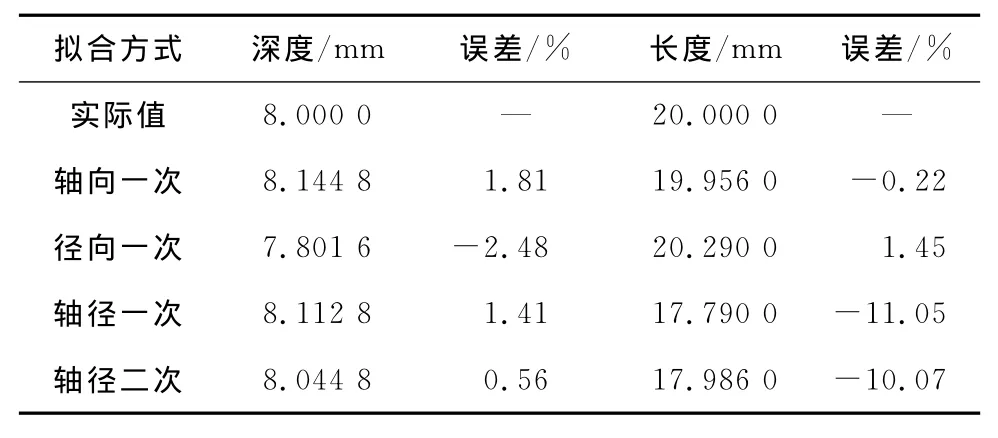
表2 实际缺陷误差分析表

由表2可知，实物试验误差分析的结果与仿真分析结果一致，验证了仿真分析结论的正确性。

6 结论

笔者将最小二乘曲线拟合原理运用到管道漏磁内检测缺陷辨识中，通过对有缺陷管壁进行漏磁内检测有限元分析，获得了管壁缺陷处漏磁场的信息。编写算法实现了单独对磁通密度轴向分量特征值和径向分量特征值进行拟合以及同时对两者进行一次和二次拟合，得到了与拟合方法相对应的拟合方程，并绘制了缺陷特征与特征值的关系曲线及缺陷量化的三维拟合曲面。

通过误差分析，确定了各类拟合方程的适用情况：对于中长度缺陷，采用轴向一次拟合方法量化精度最高；对于大长度缺陷，采用轴向径向一次拟合方程量化精度最高；对于中深度及大深度缺陷，均为采用轴向径向二次拟合方法量化精度最高；对于小长度及小深度缺陷，所述拟合方法均不能做出有效的量化。

[1]FENG Jian，ZHANG Jun－feng，LÜSen－Xiang，et al.Three－axis magnetic flux leakage in－line inspection simulation based on finite－element analysis[J].Chinese Physics B，2013，22（1）：018013－1－018103－6.

[2]HUANG Zuo ying，QUE Pei－wen，CHEN Liang.3D FEM analysis in mag net ic flux leakage method[J].NDT ＆ EInter national，2006，39（1）：61－66.

[3]林俊明.漏磁检测技术及发展现状研究[J].无损探伤，2006，30（2）：1－5.

[4]王平，赵飒，王海涛，等.钢轨表面缺陷漏磁检测的三维磁场分析[J].无损检测，2010，32（9）：658－660.

[5]刘秀清，高松巍，杨理践.ANSY在管道漏磁法检测中的研究与应用[J].沈阳工业大学学报，2001，23（1）：28－31.

[6]李久春.基于有限元的管道裂纹漏磁检测仿真分析[J].无损检测，2008，30（9）：590－593.

[7]黄松岭.管道磁化的有限元优化设计[J].清华大学学报，1998，40（2）：67－69.

[8]杨理践.管道漏磁在线检测技术[J].沈阳工业大学学报，2005，27（5）：522－525.

[9]张玉良，网沛文，黄作英.漏磁检测的仿真和实验研究[J].传感器与微系统，2006，25（8）：29－31.

[10]杨涛，王太勇，李清，等.油气管道缺陷漏磁检测试验[J].天津大学学报，2004，37（8）：686－689.

[11]黄辉，何仁洋，熊昌胜，等.漏磁检测技术在管道检测中因素分析[J].检测监测，2009，23（8）：46.

[12]郭罗军，刘丽川，江志，等.漏磁检测缺陷信号特征分析[J].无损检测，2005，27（12）：646－648.

[13]张风雷.遗传法与最小二乘法在实验数据处理中的对比研究[J].大学物理，2007，26（6）：32－34.