基于声线法的特殊体育馆模型中声场均匀性分析
2021-01-08宋恒玲
宋恒玲
(石家庄铁道大学,河北石家庄 510640)
0 引 言
体育馆除了作为单项的体育馆(或称为专用馆)外,也逐渐发展成了具有综合性功能的大型空间场馆。除了承担体育训练和竞赛的基本功能外,还要满足各类文娱演出及演讲、会议等需求。体育馆功能的扩展,必然对其室内声环境提出了更高、更综合的要求。在建筑形态方面,体育馆也由单一的几何形体转变为复杂的几何形体,设计中对曲线与曲面的运用也逐渐成熟[1]。
作为一种新的多用途大厅,对体育馆音质的研究有着现实的指导意义[2-3]。根据《体育馆声学设计及测量规程》(JGJ/T131—2000)[4],对于体育馆建筑声学设计,要求大厅应具有合适的混响时间和语言清晰度,声场均匀分布,没有回声、颤动回声、声聚焦等声缺陷。由于体育馆空间较大,对所研究频率范围的声学问题符合几何声学特点,所以可以通过声线在厅堂中的传播来研究体育馆室内声场特性,如声聚焦、颤动回声和声扩散等。
特殊体育馆模型最早被用于研究电磁混响室中电磁波的混沌现象[5-6],模型由四个矩形和两个方向不同的柱面边界构成。混沌系统有两种形成机理:扩散机理(比如Sinai模型中相邻路径与扩散体边界元的碰撞产生分离)和去聚焦机理(相邻路径与聚焦边界单元碰撞后产生聚焦,经过聚焦点之后开始发生分离,当路径足够长时,聚焦被分离所补偿导致去聚焦效果)。体育馆模型属于后者,相邻声线与柱面边界碰撞后,经过柱面焦点之后开始分离最终导致混沌行为的产生[7]。近几年已有通过声线混沌方法研究不同几何空间中声场特性的报道,如通过判定空间是否具有混沌几何特性,并进一步探索其声场特性[8-11],对于此类体育馆的声场特性分析较少见于报道。体育馆模型的混沌声线分析,对理解几何空间对声场特性的影响有重要作用。
体育馆模型的混沌特性可以通过计算声线系统的李雅普诺夫(Lyapunov)指数来判定。李雅普诺夫指数是指无限靠近的两条轨道随时间演化分离或者收敛的平均指数速率,正的Lyapunov指数意味着相邻轨道会随着时间的演化而分离,系统表现出混沌的特性[12],以λ1,λ2,λ3表示不同类型系统所有的Lyapunov指数,即Lyapunov指数谱。Lyapunov指数对系统的判定如表1所示。可以看到:对混沌系统而言,其Lyapunov指数为正,相邻轨道发生分离;对收敛系统而言,从相邻点出发的邻近轨道和基准轨道的距离逐渐变小,最终变为一个点或极限环。研究表明,Lyapunov指数与声场的扩散有关[13]:Lyapunov指数为正时声线随时间演化以指数分离,声场趋于扩散;Lyapunov指数为0时系统的声线运动呈现出规律性,声场中产生颤动回声或聚焦等声缺陷。通过计算体育馆模型的Lyapunov指数,并对比体育馆模型和矩形空间声线传播的位置和方向遍历性,可以对体育馆模型声场均匀性进行分析。

表1 不同符号Lyapunov指数谱的系统类型Table 1 The system types of different Lyapunov exponents
1 Lyapunov 指数计算
在三维空间中,声线在空间内壁碰撞反射,反射遵循反射角等于入射角的反射定律,通过跟踪声线反射后的反射点和反射线方向,得到整个反射路径的分布。
声线在三维空间中反射,有三种特殊情况:
(1) 声线在反射过程中落入角落,没有声线反射出来;
(2) 声线反射垂直于壁面,没有其他方向的声线反射;
(3) 声线在一个平面内反射,未经过其他平面。
对于情况(1)和(2),声线失去反射的连续性;在情况(3)中,声线虽然连续反射,却没有经过所有的平面,丢失了其它平面的信息。图1是声线在三维矩形和体育馆模型空间中碰撞反射的示意图。
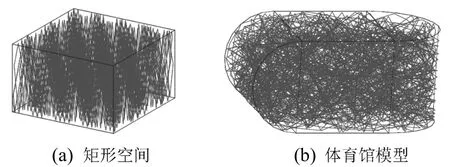
图1 矩形空间(a)和体育馆模型(b)中声线的反射Fig.1 Ray motions in (a) rectangular space and(b) stadium model
通过声线在体育馆模型内壁的反射,研究混沌结构的几何空间对声场均匀性的影响有着重要意义。设体育馆模型相对尺寸为L=5.3,W=6,H=5,矩形空间相对尺寸为L=6.8,W=6.62,H=5.1,采用Matlab 编程对声线传播路径进行模拟和混沌特性判定。对于声线系统方程未知的 Lyapunov指数计算,可以采用Wolf算法[14]。Wolf算法基于跟踪相邻轨道的指数分离情况,通过测得实验数据的时间序列计算出动力学系统的最大 Lyapunov指数,采用Wolf轨道跟踪法根据实验数据计算EL的演变和替换程序如图2所示。

图2 采用Wolf轨道跟踪法根据实验数据计算EL的演变和替换程序Fig.2 The evolution and replacement procedure using Wolf algorithm to estimate EL from experimental data
Wolf算法分为5个步骤:(1)t0时刻在轨道初始点附近寻找最近的一个邻近点,用L(t0)表示初始点和邻近点之间的距离;(2)在t1时刻这两个点分别在基准轨道和相邻轨道上的距离演化为L'(t1),计算这两个点在t1时刻的距离L'(t1)与初始时刻的距离L(t0)的比值;(3)在t1时刻寻找满足尽可能在相邻轨道方向上,即θ角最小新的邻近点,得到L(t1);(4)在时刻t2重复第(2)步;(5)对上面的过程重复M次并计算指数比。从而得到Lyapunov指数的计算公式为
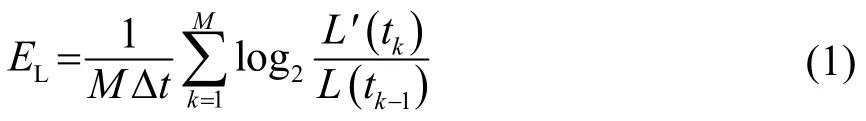
式中:∆t=tk−tk−1,M为重复次数。L'(tk)和L(tk−1)代表欧拉距离。
在 Wolf算法中,取声线反射路径上与壁面碰撞的反射点作为计算数据,以反射路径为基准轨道,在相空间中构建邻近轨道,计算随时间演化邻近轨道和基准轨道的分离指数,从而判断基准轨道是分离还是收敛。
通过计算,矩形空间Lyapunov指数为0。体育馆模型中声线系统Lyapunov指数列于表2。表2中组1和组2模型的形状有所改变,组1和组2中每个模型的形状相同,尺寸以倍数增加。
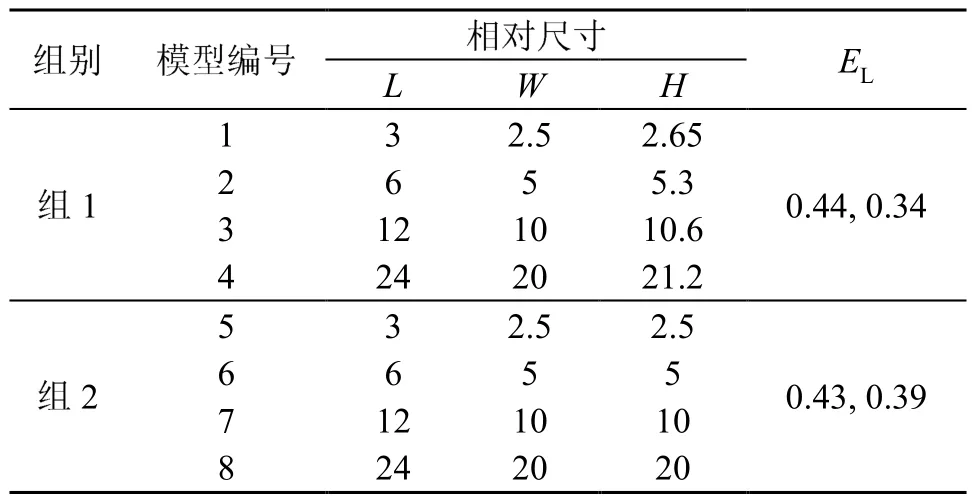
表2 几何形状不同体育馆模型中声线系统Lyapunov指数Table 2 Lyapunov exponents of ray systems in stadium model with various geometries
可以看到,当几何形状确定时(模型1, 2, 3, 4),长、宽、高比一定,Lyapunov指数相同;当几何形状改变时(如模型1和模型5,长、宽不变,高度改变),Lyapunov指数改变,因此可以得出,建筑空间几何形状决定着其中声线系统的 Lyapunov指数值。从表2中还可以看到,体育馆模型的Lyapunov指数都大于 0,其声线系统具有混沌特性。因此,体育馆模型是一个有两个正的 Lyapunov指数(EL)的超混沌结构。体育馆模型中声线发生分离,而矩形空间中声线收敛。
2 矩形空间和体育馆模型中声线位置和方向遍历性
计算 Lyapunov指数时,通过时间序列考察三维矩形和体育馆空间中声线位置和方向的遍历性。选取其中一个维度(z方向)来进行分析,时间序列分布如图3所示。
从图3可以看出,在矩形空间中声线系统的时间序列分布显示出规律性,而体育馆模型中声线系统的时间序列有着不规则的分布。计算中选择z方向,显而易见,其余方向(x、y方向)声线系统的时间序列分布也有同样的规律。对于体育馆模型中,由于存在两个正的 Lyapunov指数,其声线系统具有混沌特性;对于矩形空间,声线系统的Lyapunov指数为 0,声线系统具有规则特性。虽然声线系统时间序列分布特性不同,但在两个空间中声线最终充满整个空间,即声线反射有位置遍历性。
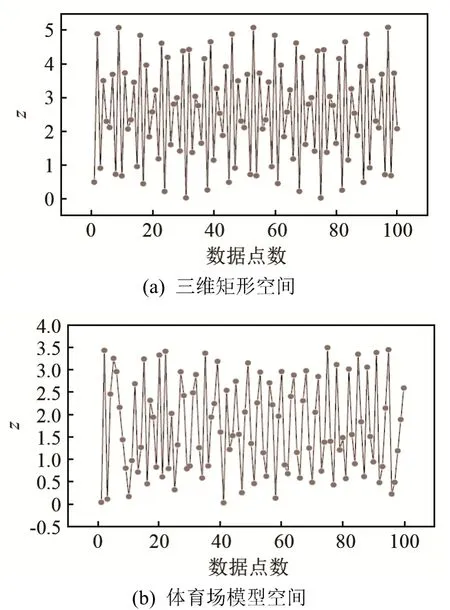
图3 三维矩形空间(a)和体育场模型空间(b)声线路径上等长度间隔100数据点的z值分布Fig.3 Distributions of z-values taken from 100 equally spaced points on the ray propagation paths for (a) rectangular space and (b) stadium model
再看两个空间中声线传播的方向分布特性。以向量表示声线的传播方向,避免上述三种特殊反射情形,通过追踪声线反射路径,可以得到,在3D矩形空间中,当声线的初始方向向量为(a,b,c)时,可以得到8种可能的传播方向(a,b,c),(a,−b,−c),(a,−b,c),(a,b,−c),(−a,−b,−c),(−a,−b,c),(−a,b,−c)和(−a,b,−c);在体育馆模型空间中,用向量空间中一个点(*)表示声线的一个方向向量。体育馆模型中声线反射 10 000次的方向向量在向量空间中x-y,y-z平面上的投影,如图4所示。
可以看出,体育馆模型空间中声线的反射可能来自空间中不同的方向,即声线具有方向遍历性。由于混沌空间中声线传播在反射过程中趋于分离,具有初值敏感性,声线行为趋于扩散[13,15]。将声线模型运用到实际声场中,矩形空间中声线虽然有位置遍历性却没有方向遍历性,在某一方向来回反射容易产生声缺陷,导致颤动回声的产生。相反,体育馆模型中声线不但具有位置遍历性,还有方向遍历性。声线反射可能来自数个不同的方向,在某一方向上集中的情况会减少。相对于形状规则的矩形空间,体育馆空间中声线的反射由于指数分离而扩散。体育馆空间中由于声线传播有着位置和方向的遍历性,从而能够得到更为均匀的声场。
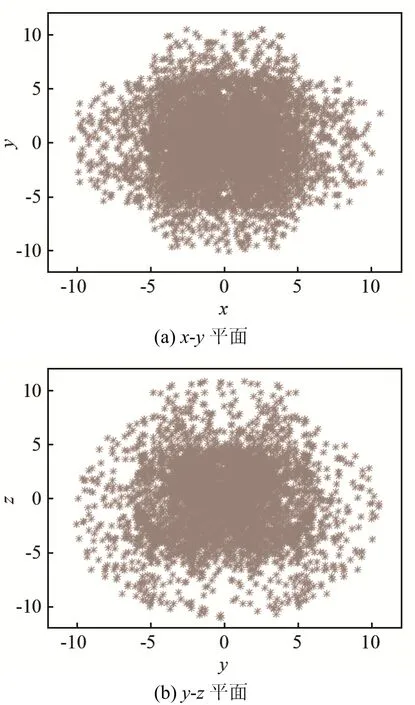
图4 体育场模型中声线方向向量在(a) x-y平面和(b) y-z平面上的投影分布Fig.4 Projection distributions of the directional vectors on (a)the x-y plane and (b) the y-z plane in stadium model
3 ODEON仿真
采用仿真软件ODEON分别对矩形空间和体育馆空间声场均匀性进行计算仿真,对声场进行网格划分,比较网格处声压级,考察声场均匀性[16]。仿真中设置声源为无指向性,壁面材质为Odeon软件材料库中提供的编号102的光滑混凝土,其吸声系数如表3所示。在软件中设置声线数为1 000,脉冲响应为1 000 ms,不考虑空气的影响,分别计算P1、P2处的声源激发的多个网格平面声压级。
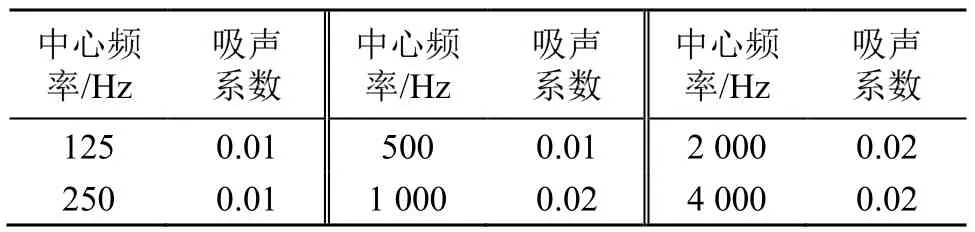
表3 壁面材质吸声系数Table 3 Absorption coefficient of wall material 102
4 结果与讨论
对体育馆模型的两个柱面之间矩形空间和 3D矩形空间采用彩色网格计算多个维度平面并做整体对比。仿真计算了中心频率 125~4 000 Hz时平面网格的声压级。图5为3D矩形空间声场分布,图6为体育馆的声场分布。由于篇幅原因,只展示了500、1 000、4 000 Hz声压级分布图。

图5 不同位置声源激发下(a) 500 Hz, (b) 1 000 Hz, (c) 4 000 Hz时3D矩形空间声场分布Fig.5 Sound field distributions at (a) 500 Hz, (b) 1 000 Hz and (c) 4 000 Hz in 3D rectangular space under the excitations of the sources at different positions

图6 不同位置声源激发下(a) 500 Hz,(b) 1000 Hz,(c) 4 000 Hz时体育馆模型声场分布Fig.6 Sound field distributions at (a) 500 Hz, (b) 1 000 Hz and(c) 4 000 Hz in stadium model under the excitations of the sources at different positions
对比图5和图6,可以看到对于不同中心频率,声源附近有着较高的声压级。在远离声源处,体育馆的声压级差异小于矩形空间,即体育馆声场均匀性均好于矩形空间。当声源位置不同时,可以得到同样的结论。
体育馆模型中声线行为基于去聚焦机理:声线经过柱面焦点后分离的长期行为抵消了柱面对声线的聚焦作用。去聚焦机理解释了体育馆模型在远离焦点的矩形位置,比3D矩形空间有更好的声场均匀性。从声线模型可以看出,体育馆空间中声线的位置和方向具有遍历性,声场中声能分布更为均匀。为方便计算,通过设置刚性光滑反射壁面得到较长的声线传播路径,由于 Lyapunov指数描述几何空间中声线的动力学行为是声线运动的趋势,需要注意的是,在足够短的声音路径情况下,体育馆模型的圆弧结构会产生聚焦。模型中多次反射是为了准确计算Lyapunov指数,由于Lyapunov指数计算是针对空间几何特性的定性描述,是声线经过多个壁面反射后发散的指数平均值,当 Lyapunov指数大于0时,混沌模型中声线系统具有混沌特性,早期声线反射经过焦点后有发散的趋势。因此,结论对圆弧结构以外的矩形空间的观众席是适用的,对于圆弧结构以内的空间,声音会产生聚焦。
附录A中以Sinai空间为例,对基于去扩散机理的混沌空间中声线传播特性进行了探讨,进一步阐述混沌结构对空间中声场均匀性的作用。
5 结 论
通过对特殊体育馆空间中声线传播路径的研究,得出这类几何形状体育馆模型声线系统具有混沌特性,声线传播有着位置和方向的遍历性。由于声线运动的混沌特性,体育馆空间中声线路径趋于发散,声场分布更加均匀。通过声学软件Odeon对体育馆和矩形空间声场仿真,得到相对于矩形空间,这类几何形状体育馆空间有着更好的声场均匀性。研究是对采用声线混沌法研究声场特性作用的补充,也为建筑声学里探索声场扩散与空间几何构型的关系提供了启发。
附录A
Sinai空间也是一个具有两个正Lyapunov指数的超混沌结构,声线系统的混沌行为基于扩散机理,图 A1为 Sinai空间中声线传播特性。图 A2和图A3同样给出了Sinai空间中声线传播位置和方向遍历性信息。
Sinai空间中声线传播位置信息如图A2所示。

图A1 扩散的Sinai空间声线反射Fig.A1 Ray motions in the Sinai spaces based on dispersion
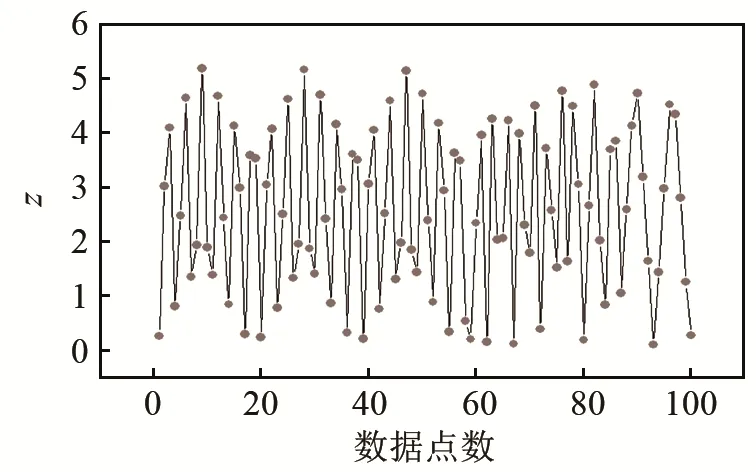
图A2 Sinai空间声线路径上等长度间隔100数据点的z值分布Fig.A2 Distributions of z-values taken from 100 equally spaced points on the ray propagation paths in the Sinai space
Sinai空间中声线传播方向信息如图A3所示。


图A3 Sinai空间中声线方向向量在x-y平面(a)和y-z平面(b)上的投影分布Fig.A3 The angular distribution of the directional vectors projected onto the x-y plane (a) and the circular distribution of the directional vectors projected onto the y-z plane (b) in the Sinai space
