三维温度梯度场中本征声线轨迹的求取*
2016-09-15何爱娜王晓宁
颜 华,何爱娜,王晓宁,2
(1.沈阳工业大学 信息科学与工程学院,沈阳 110870;2.沈阳大学 信息工程学院,沈阳 110044)
三维温度梯度场中本征声线轨迹的求取*
颜华1,何爱娜1,王晓宁1,2
(1.沈阳工业大学 信息科学与工程学院,沈阳 110870;2.沈阳大学 信息工程学院,沈阳 110044)
为了降低声波在温度梯度场中的折射现象对声学CT法温度场重建精度的影响,研究了温度梯度场中声波的真实传播路径,即本征声线轨迹,提出了一种三维本征声线出射角确定法.利用正三棱锥前向展开法,在单峰、双峰模型温度场中进行了三维本征声线追踪.结果表明,三维温度梯度场中的声线轨迹有明显弯曲,该三维本征声线轨迹求取法可用于复杂三维温度场中实际声线轨迹的确定,并有望应用于三维温度场声学CT重建系统中.
温度梯度场;本征声线;三维声线追踪;出射角;声线弯曲;声学CT;温度场重建;仿真研究
声学CT(acoustic computer tomography)温度场重建技术,又称声学法温度场检测技术,是一种先进的测温技术.该技术建立在声波在介质中的传播速度是介质温度的第一函数的基础上,通过测量从不同方向穿过被测区域的声波传播时间,推算被测区域的温度分布,具有测温范围广、测量空间范围大和非接触不干扰被测温度场等优点.工业炉温度场监测[1-2]是该技术的典型应用.而应用该技术监测仓储粮食温度分布[3-4],则是近几年开始的新的应用研究.
声学CT温度场重建包括正问题和逆问题的求解.正问题是已知声波发射/接收器的空间位置和被测区域的温度分布,求声波在各发射/接收器间的传播时间;而逆问题即温度场重建,是已知发射/接收器的位置和各发射/接收器间的声波传播时间,求解被测区域的温度分布.声学CT温度场重建可分为两步:1)建立正问题模型;2)利用正问题模型求解逆问题.目前常用的声学CT温度场重建算法主要包括:最小二乘算法[5-6]、径向基函数与正则化算法、SIRT算法[7-8]等.这些算法在建立正问题模型时,通常是将各发射/接收器间声波传播轨迹,即本征声线,按照直线处理.当非均匀温度场中出现较大温度梯度时,声波传播轨迹会因折射发生明显的弯曲现象,进而影响正问题的模化精度.如果通过声线追踪获得本征声线的传播轨迹,据此建立本征声线传播轨迹上的声波传播时间与温度分布间的关系(即正问题模型),将会显著提高温度场的重建精度.
本征声线轨迹的求取有两个关键:1)在已知声波发射器位置和声线出射角的前提下,声线轨迹的快速追踪;2)声线出射角的修正策略,其涉及到试射声线能否快速收敛到声波接收器处,即求出本征声线的出射角.其中,确定本征声线的出射角更为关键.最直接的本征声线出射角确定方法是从声源发出一束分布很密的声线,从中寻找与接收点相交的声线.这在一维或二维情形下虽然费时,但尚可行,而在三维情形下,声线方向必须用仰角和方向角两个角度才能描述,该方法几乎是不可行的.本文提出了一种三维本征声线出射角确定方法,在此基础上,采用快速的正三棱锥前向展开法追踪三维温度梯度场中声线轨迹,实现了三维温度梯度场中本征声线轨迹的求取.
1 正三棱锥前向展开声线追踪法
三维声线的正三棱锥前向展开法[9]可同时计算出声波传播路径和声波传播时间.由Snell定律可知,线性声速场中的声线轨迹为一圆弧曲线.正三棱锥前向展开法在声线路径前方伸展出一个正三棱锥区域,并将其内部近似为线性声速场,该声速场的所有必要参数都可由正三棱锥的四个顶点处的声速值确定.该方法的简述如下.
设声线入射点坐标为A(xin,yin,zin),入射方向为A(Ax,Ay,Az).以A为顶点,AH(长度为h、方向与A(Ax,Ay,Az)一致)为高作一正三棱锥,如图1所示.图1中,平面AHD垂直于平面xoz,以H到D为方向的单位矢量为HD(HDx,HDy,HDz),以E到C为方向的单位矢量为EC(ECx,ECy,ECz).存在向量关系,即EC=A×HD=(AyHDz-HDyAz,AzHDx-HDzAx,AxHDy-HDxAy).由此可求出正四面体其余顶点B、C、D的坐标.

图1 正三棱锥展开图
由于正三棱锥可以取得足够小,其内部声速场可近似为线性分布,可表示为
G(x,y,z)=ax+by+cz+d
(1)
由正三棱锥的四个顶点A、B、C、D的坐标及其顶点对应的声速值Gin、G1、G2、G3可以确定系数a、b、c、d.式(1)所描述的线性声速场的等声速面是由nc(a,b,c)为法线向量的平面族构成.入射点A所在的等声速面nc和A共同决定了声线轨迹所在的平面,其法向单位矢量为

(2)
将声线入射点A作为新坐标系的原点o′,将原坐标系绕x轴旋转β角度,绕y轴旋转α角度得到新的坐标系x′y′z′,使平面x′o′y′为声线轨迹所在的平面.在新坐标系下,平面z′=0上的声速场表达式为
G(x′,y′,z′)=a′x′+b′y′+d′
(3)
其中,
(4)
声线轨迹所在平面z′=0在原坐标系下可表示为
nx(x-xin)+ny(y-yin)+nz(z-zin)=0
(5)
平面z′=0也可表示为
z′=-sin αcos β(x-xin)-sin β(y-yin)+cos αcos β(z-zin)=0
(6)
比较式(5)、(6)可求出sin α、cos α、sin β、cos β的值.
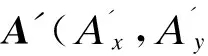
h的取值对追踪的精度和用时有较大影响,h越小,追踪精度越好,但用时也越大.一般可取h为声线起点与终点间距的1.5%~3%[10].
2 本征声线出射角的确定
本文采用多种策略降低复杂温度场中的声线出射角确定的工作量.这些策略主要包括:通过粗扫确定本征声线的大致方向,使试射密度的加大更有针对性;逐级加大试射密度,且密度越大,试射区域越小;形成试射角度矩阵后,按照试射成功的几率对试射角度排序;记录试射过的方向,避免重复试射.依据上述策略,本文提出的本征声线出射角确定法可分为粗扫与细扫两个阶段.粗扫阶段又可分为以下3个步骤.
步骤1)计算声线起点(xi,yi,zi)到接收点(xo,yo,zo)的直线方向所对应的仰角θ0和方向角φ0.
步骤2)分别以θ0和φ0为中心,δ为步长,在θ0和φ0的两侧,各形成角度间隔为δ的2N+1维仰角和方向角向量,再两两组合成(2N+1)2×2维仰角和方向角矩阵,对该矩阵按照各行与[θ0,φ0]距离由近到远排序,获得粗扫试射矩阵.
步骤3)按顺序依次用粗扫试射矩阵各行指定的方向发出声线,找到与接收面的交点距离接收点最近的声线,用[θm,φm]存储该声线的仰角和方向角.如某一声线对应的交点与接收点的距离小于预先规定好的误差限E0,则不进行后面的试射,跳出粗扫阶段.
粗扫阶段,取h为声线起点与终点间距的3%.粗扫结束后,则取h为声线起点和终点间距的1%.按[θm,φm]指定的方向发射一声线,求出声线与接收平面的交点,并用Lmin记录交点与接收点的距离,令n=0进入细扫阶段.细扫阶段为一循环结构,可分为以下4个步骤.
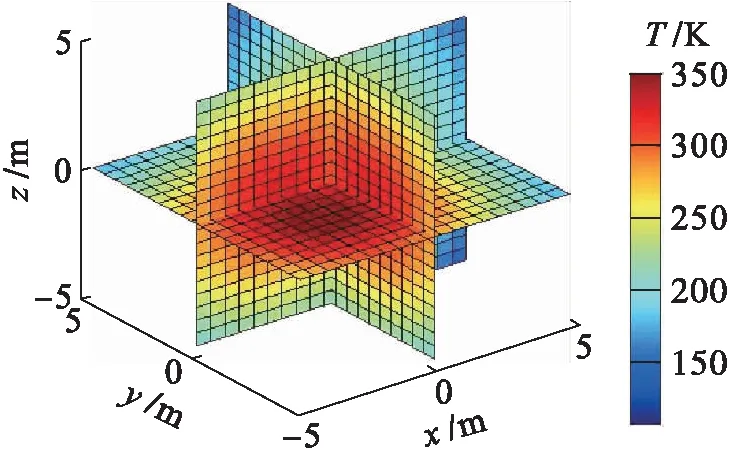
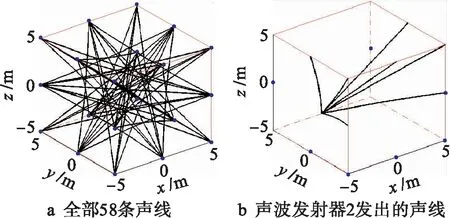
步骤1)判断是否满足Lmin>E1且n 步骤2)分别以θm和φm为中心,δ/2n为步长,在θm和φm的两侧,各形成角度间隔为δ/2n的5维仰角和方向角向量,再两两组合成25×2维仰角和方向角矩阵,剔除其中试射过的声线后按照各行与[θm,φm]距离由近到远排序,获得细扫试射矩阵. 步骤3)按顺序依次用细扫试射矩阵各行指定的方向发出声线,找到与接收面的交点距离接收点最近的声线,并用θ、φ和L存储该声线的仰角、方向角以及交点与接收点的距离.如某一声线对应的交点与接收点的距离小于E1,则不进行后面的试射,直接进入步骤4). 步骤4)如果L 粗扫只是确定出射角的大致方向,故E0可取得较大以减少用时.E1越小,本征声线轨迹计算精度越高,但需要更大的n值,更小的步长δ,细扫的用时也越长. 本文所考虑的被测区域为10 m×10 m×10 m的正方体区域,周围布置20个声波发射/接收器,如图2所示.其中,蓝色圆点表示声波发射/接收器,红线表示区域边界. 图2 声波发射/接收器布局 采用本文所提出的方法,在多个单峰、双峰模型温度场中,求取本征声线轨迹.计算中取E0=1.5,E1=0.01,n0=10,δ=3°.由于篇幅所限,本文只给出了4个模型温度场中的本征声线求取结果. 模型温度场1,其表达式为 (7) 该温度场最高温度为350 K,最低温度为103 K.图3为温度场的截面图.图4为该温度场中的声线轨迹.其中,声线轨迹相对于直线声线的最大偏差为3.900 m,平均偏差为1.249 m. 图3 模型温度场1 图4 模型温度场1中的声线轨迹 模型温度场2,其表达式为 T(x,y,z)=293+40e-0.05(x2+y2+z2) (8) 该温度场最高温度为333 K,最低温度为294 K.图5为温度场的截面图.图6为该温度场中的声线轨迹.其中,声线轨迹相对于直线声线的最大偏差为0.629 m,平均偏差为0.270 m. 图5 模型温度场2 图6 模型温度场2中的声线轨迹 模型温度场3,其表达式为 (9) 该温度场最高温度为457 K,最低温度为69 K.图7为温度场的截面图.图8为该温度场中的声线轨迹.其中,声线轨迹相对于直线声线的最大偏差为2.344 m,平均偏差为1.574 m. 图7 模型温度场3 图8 模型温度场3中的声线轨迹 模型温度场4,其表达式为 T(x,y,z)=293+50e-0.09[(x-3)2+y2+(z-0.6)2]+ 50e-0.09[(x+3)2+y2+(z-0.6)2] (10) 该温度场最高温度为346 K,最低温度为293 K.图9为温度场的截面图.图10为该温度场中的声线轨迹.其中,声线轨迹相对于直线声线的最大偏差为0.375 m,平均偏差为0.245 m. 图9 模型温度场4 图10 模型温度场4中的声线轨迹 由Snell法则可知,声线会由于折射现象而向低声速(低温)的方向弯曲.声速(温度)差别越大,这种弯曲越明显.上述本征声线轨迹也验证了这一现象. 正三棱锥前向展开法的基础是几何声学,其只要求声波的波长与散射体的尺寸相比十分小,对温度场没有特殊的要求.因此,本文所提出的本征声线轨迹求取法,原则上可用于任何类型的三维温度场. 声波在温度梯度场中的传播轨迹会因折射而弯曲.本文所提出的本征声线轨迹求取法,具有算法简单、结果可靠和计算精度容易控制等优点,可用于复杂三维温度场中实际声线轨迹的确定.而声波在不同温度场中的传播轨迹的先验信息,将有助于提高温度场重建的精度和速度.因此,本文所提出的三维本征声线轨迹求取法,有望应用于三维温度场声学CT重建系统中. [1]Bramanti M,Salerno E A,Tonazzini A,et al.An acoustic pyrometer system for tomographic thermal imaging in power plant boilers [J].IEEE Transactions on Instrumentation and Measurement,1996,45(1):159-167. [2]Zhang S P,Shen G Q,An L S,et al.Online monitoring of the two-dimensional temperature field in a boiler furnace based on acoustic computed tomography [J].Applied Thermal Engineering,2015,75:958-966. [3]Yan H,Chen G,Zhou Y,et al.Primary study of temperature distribution measurement in stored grain based on acoustic tomography [J].Experimental Thermal and Fluid Science,2012,42(10):55-63. [4]王善辉,颜华,李爽.声学CT储粮温度监测收发器阵列设计 [J].沈阳工业大学学报,2014,36(5):561-566. (WANG Shan-hui,YAN Hua,LI Shuang.Design for transceiver array of temperature in stored grain monitored by acoustic CT [J].Journal of Shenyang University of Technology,2014,36(5):561-566.) [5]毛洁,吴友凤,樊炜,等.声学法深海热液温度场测量及重建算法研究 [J].仪器仪表学报,2010,31(10):2339-2344. (MAO Jie,WU You-feng,FAN Wei,et al.Acoustic temperature field measurement in deep-sea hydrothermal vents and reconstruction algorithm [J].Chinese Journal of Scientific Instrument,2010,31(10):2339-2344.) [6]Fan W,Chen Y,Pan H C,et al.Experimental study on underwater acoustic imaging of 2-D temperature distribution around hot springs on floor of Lake Qiezishan,China [J].Experimental Thermal and Fluid Science,2010,34(8):1334-1345. [7]Barth M,Armin R.Acoustic tomographic imaging of temperature and flow fields in air [J].Measurement Science and Technology,2011,22(3):1-13. [8]Fischer G,Barth M,Ziemann A.Acoustic tomography of the atmosphere:comparison of different reconstruc-tion algorithms [J].Acta Acustica United with Acustica,2012,98(4):534-545. [9]姜薇,李太宝.三维声线追踪的正三棱锥前向伸展算法 [J].声学学报,2005,30(5):404-408. (JIANG Wei,LI Tai-bao.A three-dimensional sound ray tracing method by deploying regular tetrahedrons [J].Acta Acustica,2005,30(5):404-408.) [10]颜华,王善辉,刘丽钧,等.一种考虑声线弯曲的温度场重建算法 [J].声学学报,2014,39(6):705-713. (YAN Hua,WANG Shan-hui,LIU Li-jun,et al.A reconstruction algorithm of temperature field taking into account the bending of sound wave paths [J].Acta Acustica,2014,39(6):705-713.) (责任编辑:钟媛英文审校:尹淑英) Solution of eigen acoustic ray paths in three-dimensional temperature gradient field YAN Hua1,HE Ai-na1,WANG Xiao-ning1,2 (1.School of Information Science and Engineering,Shenyang University of Technology,Shenyang 110870,China; 2.School of Information Engineering,Shenyang University,Shenyang 110044,China) To reduce the effect of sound wave refraction in temperature gradient field on the reconstruction accuracy of temperature field by acoustic computer tomography (CT),the true propagation paths of acoustic ray in temperature gradient field,namely the eigen acoustic ray paths,were investigated.A method for determining the emergent angle of three-dimensional eigen acoustic ray was proposed.And thus,the three-dimensional eigen acoustic ray was traced in single-peak and dual-peak model temperature fields with the regular tetrahedron forward development method.The results show that the acoustic ray paths in three-dimensional gradient field have obvious bending effect.The proposed solution method for three-dimensional eigen acoustic ray paths can be used for determining the true acoustic ray paths in complex three-dimensional temperature field,and is expected to be applied to the acoustic CT reconstruction system of three-dimensional temperature field. temperature gradient field; eigen acoustic ray; three-dimensional acoustic ray tracing; emergent angle; acoustic ray bending; acoustic CT; temperature field reconstruction; simulation research 2015-06-30. 国家自然科学基金资助项目(60772054,61372154);辽宁省高等学校优秀人才支持计划项目(LR2013005). 颜华(1964-),女,辽宁沈阳人,教授,博士生导师,主要从事声学法温度场检测和电容层析成像技术等方面的研究. 10.7688/j.issn.1000-1646.2016.02.12 TK 311 A 1000-1646(2016)02-0185-05 *本文已于2015-09-15 09∶09在中国知网优先数字出版.网络出版地址:http://www.cnki.net/kcms/detail/21.1189.T.20150915.0909.038.html 信息科学与工程3 三维温度梯度场中本征声线的求取





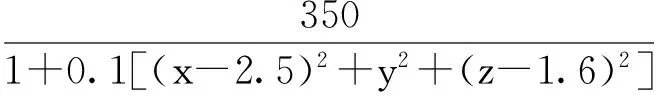


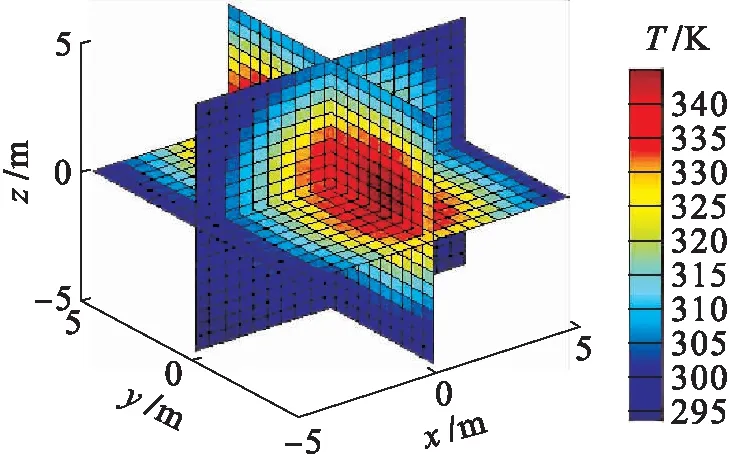
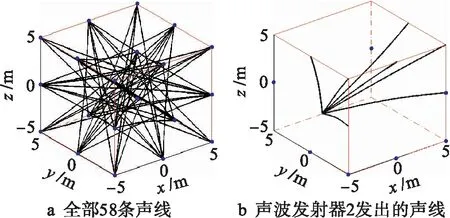
4 结 论
