关于k-sum-avoiding子集基数的估计
2014-07-19赵青青
赵青青
(河海大学文天学院,安徽马鞍山243031)
关于k-sum-avoiding子集基数的估计
赵青青
(河海大学文天学院,安徽马鞍山243031)
对sum-avoiding子集进行推广,对任意正整数k(k≥2),若集合S是A⊆N的一个子集,且S中任意k个元素的和都不属于A,则S称为集合A的k-sum-avoiding子集.估计了当|A|=n时,A的k-sum-avoiding子集S的最大基数.
sum-avoiding子集;最大基数;k-sum-avoiding子集
1 前言和主要结果
若S是集合A⊆N的一个子集,且S中任意两个不同元素的和都不属于A,则S称为集合A的sum-avoiding子集.
用λ(A)记A的sum-avoiding子集的最大基数,且
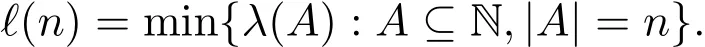
1971年,文献[1]证明了ℓ(n)≪n2/5+o(1).2005年,文献[2]证明了如下结论:
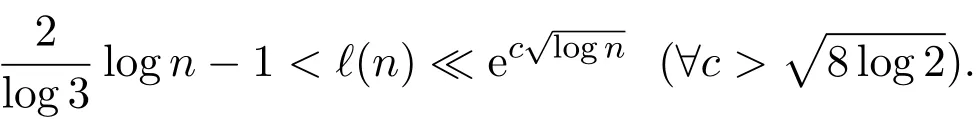
这也是目前最好的上界.文献[2]证明上界的方法与Behrend在文献[3]中用到的方法有些类似.同一年,文献[4]将ℓ(n)的下界改进到lognlogloglogloglogn.
受文献[5]启发,本文对sum-avoiding子集进行推广.对任意正整数k(k≥2),若集合S是A⊆N的一个子集,且S中任意k个不同元素的和都不属于A,则S称为集合A的k-sum-avoiding子集.用λk(A)记A的k-sum-avoiding子集的最大基数,且
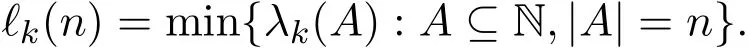
对ℓk(n)的上界进行估计,得到如下结论.
定理1.1对任意正整数k(k≥2),特别地,取k=2,可以得到文献[2]的结果.
2 引理
引理2.1设正整数d≥2,b1,b2,···,bk为中的k(k≥2)个不同的向量.若
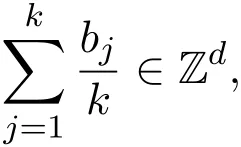
且对每个j(1≤j≤k)都有
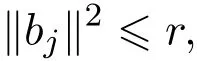
则
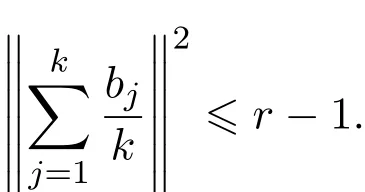
证明由三角不等式,有
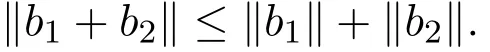
将此不等式推广到k个向量可得,
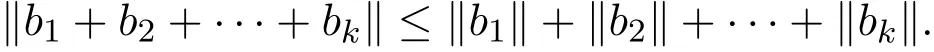
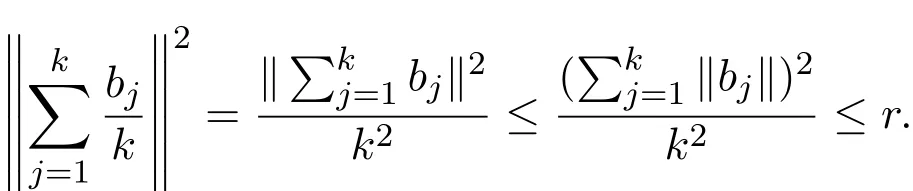
上述等号成立当且仅当所有的向量bj(1≤j≤k)共线且满足各不相同,故上述等号不成立.因此
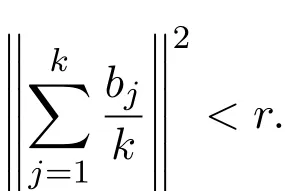
又因为
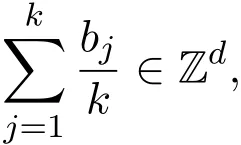
故
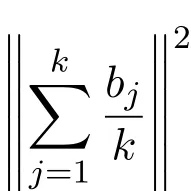
为整数.因此
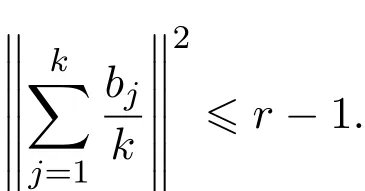
引理2.2(Erds-Ginzburg-Ziv定理[6])设n≥1,若a0,a1,···,a2n−2是2n−1个不同整数构成的数列,则一定存在一个子数列ai1,ai2,···,ain,使得
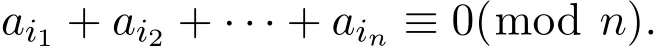
3 定理
引理3.1对任意正整数
证明首先,选取恰当的d,构造集合E⊆Zd,使得|E|>n,且对于任意有
给定一个正整数r,定义
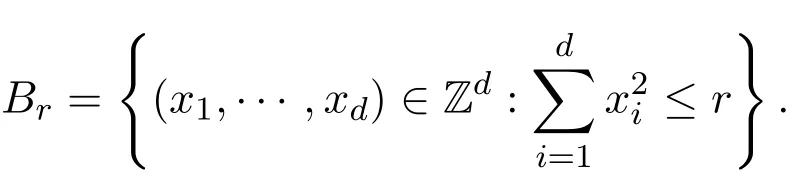
考虑集合
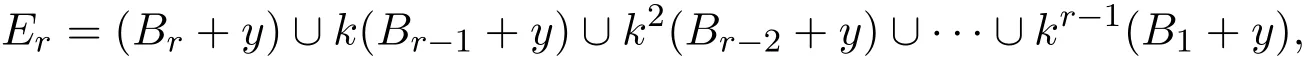
其中kB={kb:b∈B},y∈Zd为任意的.
下面证明
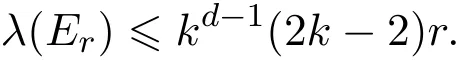
任取一k-sum-avoiding子集S⊆Er.若|S|>kd−1(2k−2)r,则必存在i(0≤i≤r−1),使得
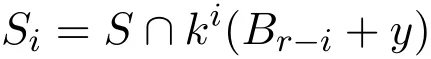
且满足
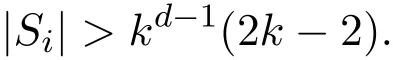
又因为当d≥3时,
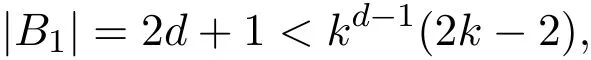
故i
因此对任意的j=0,1,···,kd−1(2k−2),存在b0,b1,···,bkd−1(2k−2)∈Br−i,使得

由抽屉原理知存在一子集

其中|B′|>2k−2使得如下结论成立.对于任意的c1,c2∈B′和j∈{2,3,···,d},都有
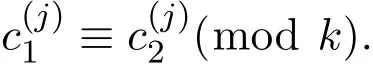

其中c(i)表示向量c的第i个分量.因此由引理2.2知,存在k个向量bi1,bi2,···,bik∈B′满足:

又因为
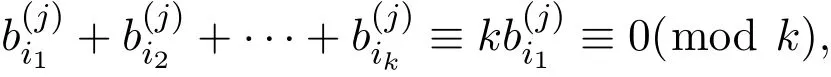
可得

由引理2.1知

故b∈Br−i−1.因此当j=1,2,···,k且ki(bij+y)∈S时,有

矛盾.
接着对|Er|进行估计.若对每个则显然

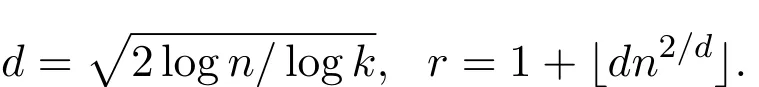
这样就有
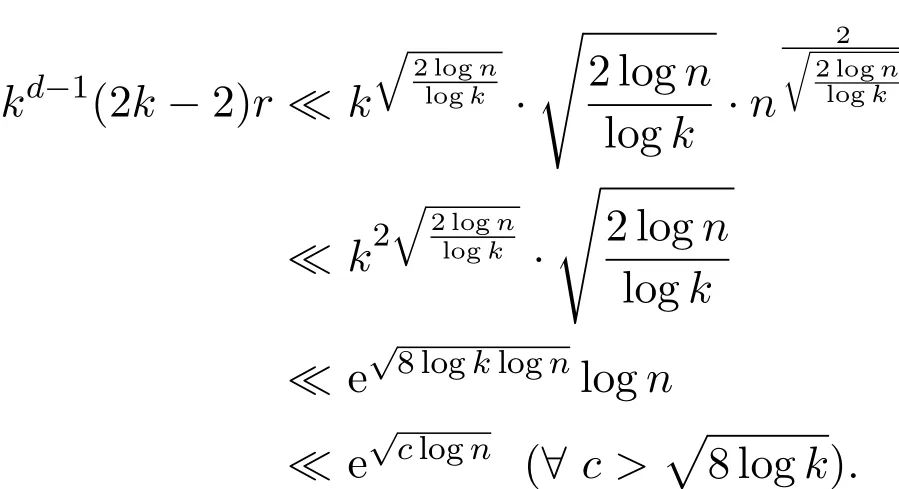
下面作映射
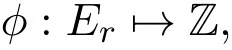
显然这个映射保持集合的基数和加法关系不变.设A1是映射ϕ:ErBZ_74_1646_2840_1692_2886的像集.取y充分大,则像集A1的元素全为正整数,且
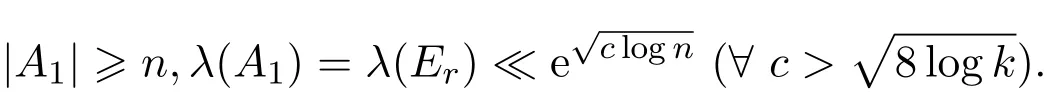
最后,取A1中最大的n个元素构成集合A.显然A中任意k个不同元素之和不属于A1A,故
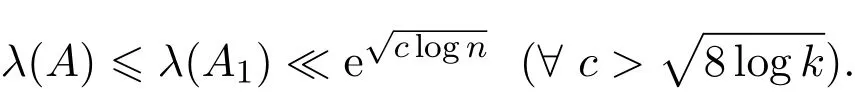
[1] Choi S L G.On a combinatorial problem in number theory[J].Proc.London Math.Soc.,1971,23:629-641.
[2] Rusza I Z.Sum-avoiding subsets[J].Ramanujan J.,2005,9:77-82.
[3] Behrend F A.On sets of integers which contain no three terms in arithmetical progression[J].Proc.Nat. Acad.Sci.,1946,32:331-332.
[4] Sudakov B,Szemer´edi B and Vu V H.On a question of Erd¨os and Moser[J].Duke Math.,2005,129:129-155.
[5] 崔丽雯,杨胜良.广义的k阶Fibonacci-Jacobsthal序列[J].纯粹数学与应用数学,2011,27(6):819-824.
[6] Erd¨os P,Ginzburg A,Ziv A.Theorem in the additive number theory[J].Bull.Research Council Israel., 1961,10F:41-43.
On the cardinality of k-sum-avoiding subsets
Zhao Qingqing
(Wentian College,Hohai University,Maanshan243031,China)
For a positive integer k,we call a subset S⊆A k-sum-avoiding,if any sum of k distinct elements taken from S does not belong to A.In this paper,we estimate the maximal cardinality of k-sum-avoiding subsets S of A when|A|=n.
sum-avoiding subsets,maximal cardinality,k-sum-avoiding subsets
O156.1
A
1008-5513(2014)05-0507-05
10.3969/j.issn.1008-5513.2014.05.012
2014-05-20.
赵青青(1985-),硕士,讲师,研究方向:数论.
2010 MSC:11A10
