Filiform李超代数Ln,m的导子和保积Hom-结构
2014-07-19焦阳刘文德
焦阳,刘文德
(哈尔滨师范大学数学科学学院,黑龙江哈尔滨150025)
Filiform李超代数Ln,m的导子和保积Hom-结构
焦阳,刘文德
(哈尔滨师范大学数学科学学院,黑龙江哈尔滨150025)
将李超代数的导子和Hom-结构表示为矩阵,通过计算,具体刻画了特征零的代数闭域上Filiform李超代数Ln,m的导子代数和保积Hom-结构.
Filiform李超代数;导子;Hom-结构
1 引言
Hom-结构以及导子代数是李超代数结构理论研究中活跃而重要的课题.2006年,Larsson和Silvestrov为了研究Witt代数与Virasoro代数的形变,提出了Hom-李代数的概念[1]. 2010年,F.Ammar和A.Makhlouf将Hom-李代数推广到Hom-李超代数上[2].2011年,邹旭娟和刘文德确定了特征p>3的域上外代数与有限维广义Witt李代数的张量积所构成的李超代数的导子代数[3].2013年,曹彬涛和罗栗证明了复数域上有限维单李超代数只有平凡的保积Hom-李超代数结构[4].2014年,远继霞、孙丽萍和刘文德在复数域上的向量场单李超代数上获得了类似的结果[5].同年,高宇佳、孙丽萍和刘文德证明了单Hom-李超代数没有任何非平凡理想并且给出了保积Hom-李超代数的若干性质[6];陈翠和连海峰利用导子和三元导子的定义,刻画了特征不等于2的代数闭域上4维幂零李代数的导子和三元导子[7].
Filiform李超代数作为特殊的幂零李超代数,研究其结构对于研究幂零李超代数来说意义重大.本文刻画了特征零的代数闭域上Filiform李超代数Ln,m的导子代数和保积Hom-结构.首先介绍李超代数的导子代数及保积Hom-结构的基本概念;其次刻画Filiform李超代数Ln,m的导子代数;最后给出Ln,m的保积Hom-结构及其证明.
2 基本概念
一个F-代数A称为超代数,如果作为向量空间它是一个超空间A=A¯0⊕A¯1,并且满足相容性设A=A¯0⊕A¯1是域F上的超代数,如果它的乘法[·,·]满足斜超对称性和超Jacobi等式,那么称A是F上的李超代数[8].
定义2.1[9]设G=G¯0⊕G¯1是幂零李超代数,称G的超幂零指数为(p,q),如果(p,q)满足:
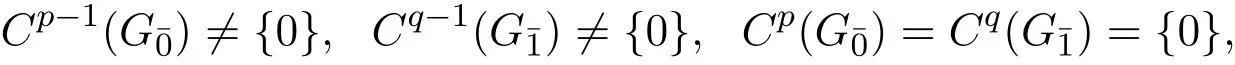
其中
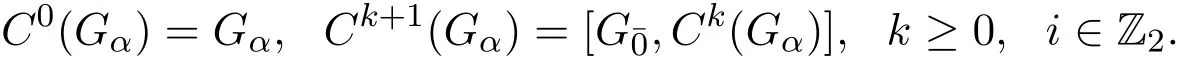
若这个幂零李超代数的超幂零指数是(dimG¯0−1,dimG¯1),则称它为Filiform李超代数.
定义2.2[8]设L=L¯0⊕L¯1为域F上的李超代数,若L上的线性变换D满足:
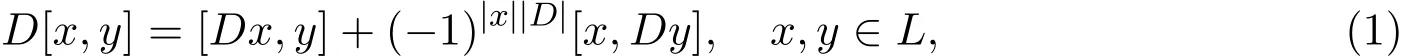
则称D是L的Z2-次数为|D|的齐次导子.令Derµ(L)表示L的Z2-次数为µ的导子的集合,其中µ∈Z2,称李超代数Der(L)=Der¯0(L)⊕Der¯1(L)为L的导子代数.
定义2.3[5]设(G,[·,·])是一个李超代数,α:G→G是一个线性映射,若α满足:
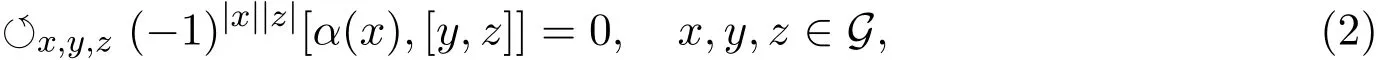
则称(G,[·,·],α)为Hom-李超代数,称α为李超代数G的Hom-结构.若α还是G的自同态,即满足

则称α为李超代数G的保积Hom-结构.
3 Filiform李超代数Ln,m的导子代数
Filiform李超代数Ln,m具有一个标准基{X0,X1,···,Xn|Y1,Y2,···,Ym},其中X0,X1,···,Xn为偶的,Y1,Y2,···,Ym为奇的;其乘法表为:
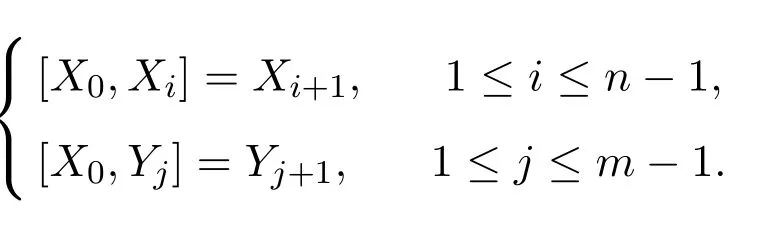
其它标准基元素的方括号均为0.
令D是Filiform李超代数Ln,m的导子,偶导子在该组基下的矩阵用

表示.
Filiform李超代数的导子代数用Der(Ln,m)表示,则有以下定理:
定理3.1Filiform李超代数的导子代数Der(Ln,m)的基如表1所示.

表1 导子代数Der(Ln,m)的基表示
为得到定理3.1,首先证明引理3.1和引理3.2.
引理3.1Filiform李超代数Ln,m的偶导子具有如下形式:
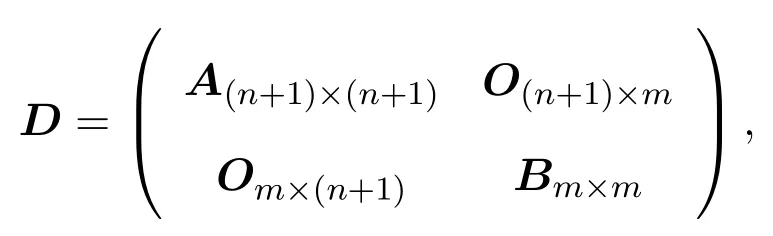
其中,O为零矩阵,矩阵A中元素xij由表2给出,矩阵B中元素yn+k+1,n+l+1由表3给出.
证明由导子定义易知,D是Ln,m的导子当且仅当任意基中元素均满足(1)式.
当D是偶导子时,分三种情况讨论:(1)x,y均不为X0;(2)x,y均为X0;(3)x,y中有且只有一个为X0.由(1)式,得
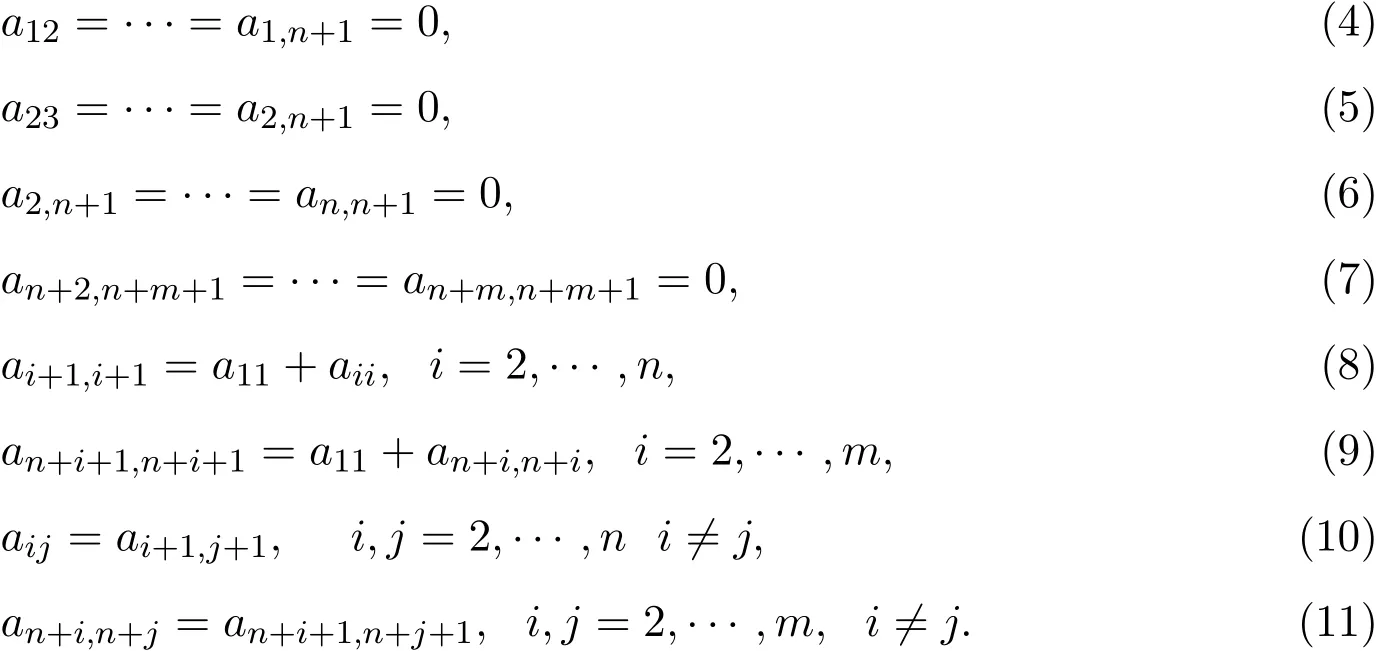
由(4)式-(11)式,Filiform李超代数Ln,m的偶导子
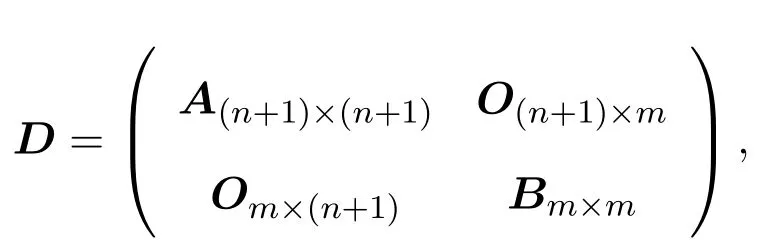
其中,O为零矩阵,矩阵A中元素xij由表2给出.

表2 矩阵A中元素xij
记x11,···,xn+1,1分别为a,a1,···,an;x22,···,xn+1,2分别为a,b1,···,bn.矩阵B中元素yn+k+1,n+l+1由表3给出.记yn+2,n+2,···,yn+m+1,n+2分别为c1,···,cm.

表3 矩阵B中元素yn+k+1,n+l+1
下面计算Filiform李超代数Ln,m的奇导子.Filiform李超代数Ln,m的奇导子在该组基下的矩阵用

表示,此时导子D分三种情况讨论:(1)x,y均不为X0;(2)x,y均为X0;(3)x,y中有且只有一个为X0.由(1)式,得
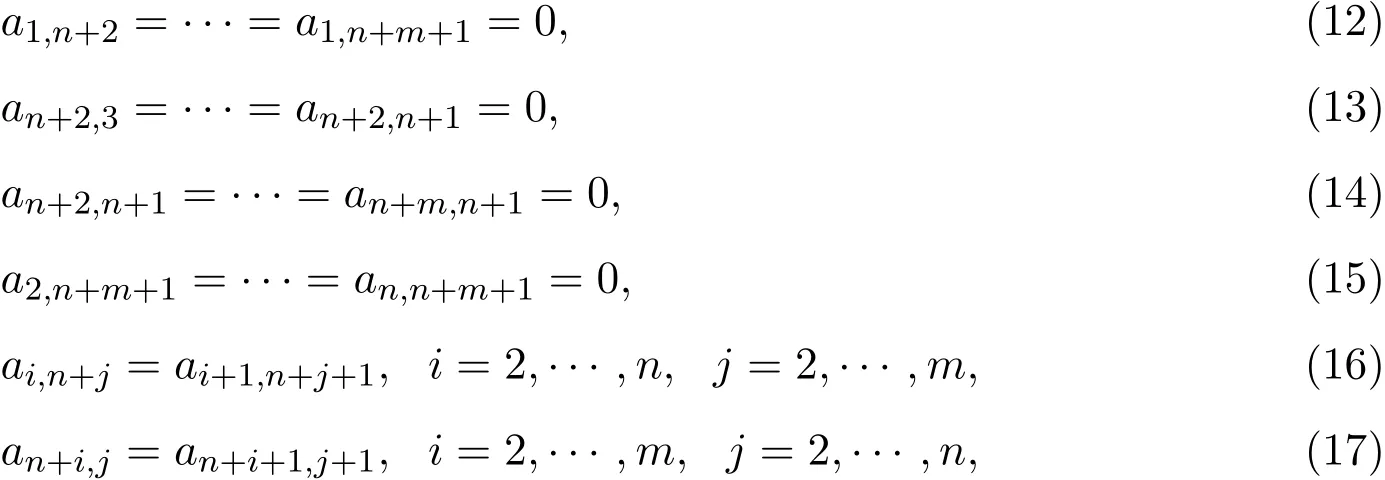
由(12)式-(17)式,Filiform李超代数Ln,m的奇导子

其中,O为零矩阵,矩阵E和矩阵F中元素有以下三种情形:
当m=n时,矩阵E中元素xn+i,j由表4给出.
记xn+3,2,···,xn+m,2分别为e1,···,em−2.矩阵F中元素yk,n+l由表5给出.
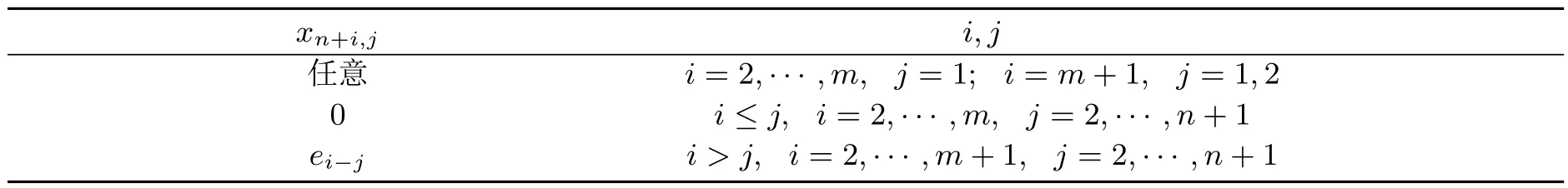
表4 矩阵E中元素xn+i,j
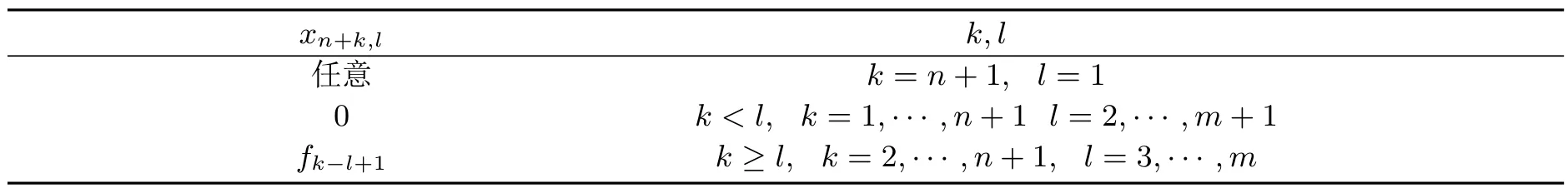
表5 矩阵F中元素yk,n+l
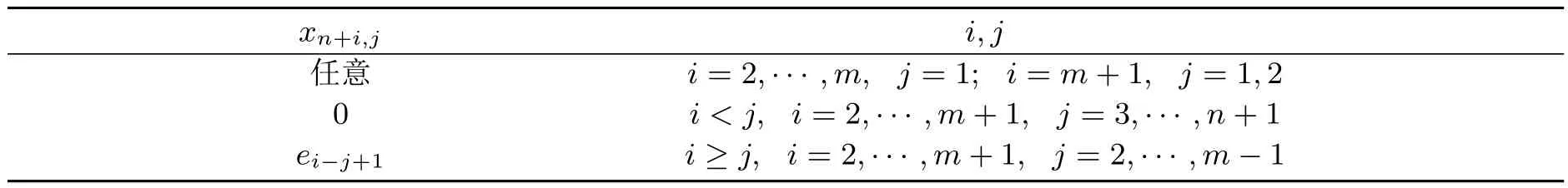
表6 矩阵E中元素xn+i,j
记y2,n+2,···,yn,n+2分别为f1,···,fn−1.
当m 记xn+2,2,···,xn+m,2分别为e1,···,em−1.矩阵F中元素yk,n+l由表7给出. 表7 矩阵F中元素yk,n+l 记yn−m+2,n+2,···,yn+m,n+2分别为f1,···,fm−1. 当m>n时,矩阵E中元素xn+i,j由表8给出. 表8 矩阵E中元素xn+i,j 记xm−n+1,2,···,xn+m,2分别为e1,···,em−1.矩阵F中元素yk,n+l由表9给出. 记y2,n+2,···,yn,n+2分别为f1,···,fn;y2,n+3,···,y2,m+2分别为g1,···,gm−n. 由此可得到引理3.2: 表9 矩阵F中元素yk,n+l 引理3.2Filiform李超代数Ln,m的奇导子具有如下形式: 其中,O为零矩阵.当m=n时,矩阵E中元素xn+i,j由表4给出,矩阵F中元素yk,n+l由表5给出;当m 由引理3.1和引理3.2,即得定理3.1. 令α是Filiform李超代数Ln,m的保积Hom-结构,α在基{X0,X1,···,Xn|Y1,Y2,···,Ym}下的矩阵用 表示. 定理4.1Filiform李超代数Ln,m的保积Hom-结构具有如下形式: 其中,O为零矩阵, 这里a,a1,···,an,b1,···,bn,c1,···,cm是任意的,且 证明由保积Hom-结构定义易知,α是Filiform李超代数Ln,m的保积Hom-结构当且仅当任意基元素均满足(2)式-(3)式. 首先,(2)式中x,y,z取遍标准基{X0,X1,···,Xn|Y1,Y2,···,Ym}中所有元素,分五种情况讨论:(1)x,y,z均不为X0;(2)x,y,z均为X0;(3)x,y,z中有两个为X0;(4)x,y,z中有且只有一个为X0,且其余两个基相同;(5)x,y,z中有且只有一个为X0,且其余两个基不同.得 其次,(3)式中x,y取遍标准基{X0,X1,···,Xn|Y1,Y2,···,Ym}中所有元素,分三种情况讨论:(1)x,y均不为X0;(2)x,y均为X0;(3)x,y中有且只有一个为X0.得 由(18)式-(22)式,Filiform李超代数Ln,m的保积Hom-结构 其中,O为零矩阵, 这里a,a1,···,an,b1,···,bn,c1,···,cm是任意的,且 [1] Larsson D,Silvesrov S.Quasi-Hom-derformations of sl2(F)using twisted derivations[J].Comm.Algebra, 2007,35:4303-4318. [2] Ammar F,Makhlouf A.Hom-Lie superalgebras and Hom-Lie admissible superalgebras[J].J.Algebra, 2010,324:1513-1528. [3] 邹旭娟,刘文德.一类Witt型李超代数的超导子代数[J].数学杂志,2011,31:469-475. [4] Cao B,Luo L.Hom-Lie superalgebra structures on fi nite-dimensional simple Lie superalgebras[J].J.Lie Theory,2013,23:1115-1128. [5] Yuan J,Sun L,Liu W.Hom-Lie superalgebra structures on in fi nite-dimensional simple Lie superalgebras of vector fi elds[J].J.Geom.Phys.,2014,84:1-7. [6] 高宇佳,孙丽萍,刘文德.Hom-李超代数的结构[J].纯粹数学与应用数学,2014,30:186-194. [7] 陈翠,连海峰.4维幂零李代数的导子与triple导子[J].数学的实践与认识,2014,5:62-68. [8] Kac V.Lie superalgebras[J].Adv.Math.,1977,26:8-96. [9] Khakimdjanov Y,Navarro R.A complete description of all the in fi nitesimal deformations of the Lie superalgebra Ln,m[J].J.Geom.Phys.,2010,60:131-141. The derivations and the multiplicative Hom-structures of Filiform Lie superalgebras Ln,m Jiao Yang,Liu Wende Let F be an algebraically closed fi eld of characteristic zero.In this paper,we characterize the derivations and the multiplicative Hom-structures of Filiform Lie superalgebras Ln,mover F in terms of matrices. Filiform Lie superalgebras,derivations,Hom-structures O152.5 A 1008-5513(2014)05-0534-09 10.3969/j.issn.1008-5513.2014.05.015 2014-08-11. 国家自然科学基金(11171055,11471090);黑龙江省教育厅科学技术研究项目(12541246,12541184);黑龙江省自然科学基金(A201412). 焦阳(1990-),硕士,研究方向:李超代数. 2010 MSC:22E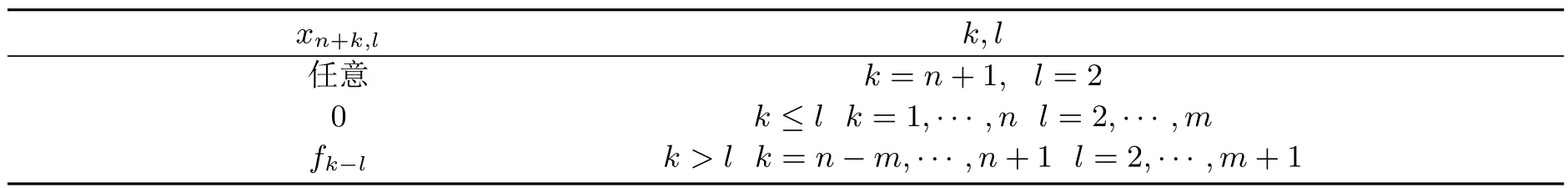
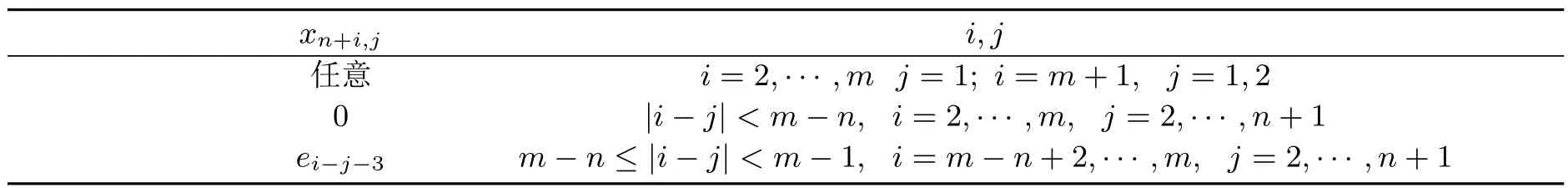

4 Filiform李超代数Ln,m的保积Hom-结构

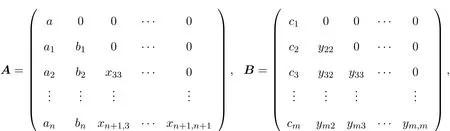
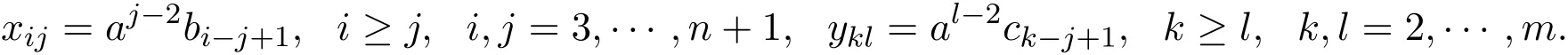


(Department of Mathematics,Harbin Normal University,Harbin150025,China)
