置换性很好的一类群
2014-07-19钟艳林曾吉文
钟艳林,曾吉文
(1.闽南理工学院信息管理系,福建泉州362700;2.厦门大学数学科学院,福建厦门361005)
置换性很好的一类群
钟艳林1,曾吉文2
(1.闽南理工学院信息管理系,福建泉州362700;2.厦门大学数学科学院,福建厦门361005)
主要研究子群置换性质对有限群结构的影响.通过子群的置换性得到一类群,即B群.B群是全可置换群的扩展,利用全可置换群的p次中心扩张和子群的阶得到B群的一些性质并对B群的结构进行一些刻画.应用B群的结构得到有限p(p>2)群为二元生成的B群的充要条件.关键词:有限群;B群;有限p群
1 基本知识
设G是有限群,记S1(G)={H|H是G的素数幂阶群},S2(G)={H|H是G的素数阶群,且|H|2||G|},若HΦ(G),K∈S1(G),总有HK=KH,则称G是一个A群.若HΦ(G),K∈S1(G)−S2(G),总有HK=KH,则称G是一个B群.如果G是A群,则G是全可置换群(见文献[1]定理1.2).
从定义出发,可以得到这样的结论:若G是A群,则G是B群.若G是A群,则可以认为不包含于Φ(G)的子群的置换性强,G是全可置换群.这样的群的结构已知(见文献[2]).若G是B群,则认为不包含于(G)的子群的置换性稍弱一些.由定理2.1可以看出,G就是幂零群.提出问题:若G是B群,则G是怎样的?
2 主要结论及证明
定理2.1设G是B群.则
(1)G是幂零群.
(2)若P是G的一个Sylow子群,则G/P是B群.
(3)若P是G的一个Sylow子群,则P是B群.若1̸=NP,则P/N是A群.
(4)若G是有限p群且不是A群,则G是外A群.
证明(1)任取P∈Sylp(G),其中,Sylp(G)表示G的Sylow子群,由p||G/Φ(G)|可知, P̸∈Φ(G).任取P1∈Sylp(G),则PP1=P1P.由

可知,|PP1|=|P|.因此P1⊆P.则G的Sylow p子群唯一.因此G是幂零群[3].
(2)设H/P≤G/P且H/P̸≤Φ(G/P),K/P≤G/P且K/P∈S1(G/P)−S2(G/P).由G是幂零群,则可设

其中P是G的Sylow子群.因此K=K×P,其中K∩P=1.容易得到:
i11


因此HK=KH.则H/PK/P=K/PH/P.因此G/P是B群.
(3)由B群的定义易得P是B群.设H/N≤P/N且H/N̸≤Φ(P/N),K/N≤P/N.不妨设

则|K|≥p2.从而K∈S1(P)−S2(P).由H̸≤(P)可知,
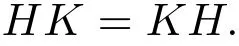
则H/NK/N=K/NH/N.因此P/N是A群.
(4)由G不是A群以及(3)可知结论.
由定理2.1(1)可知,一个B群为其Sylow子群的直积,故应该对其Sylow子群进行研究.由定理2.1(3)可知,一个B群的Sylow子群也是B群.因此对B群为有限p群进行研究.
定理2.2设G是一个非交换的有限p群.若G是B群,则存在H≤G′∩Z(G),|H|=p,使得G/H是全可置换群.
证明取H≤G′且H是G的一个p阶正规子群.显然H≤Z(G)[4].由定理2.1(3)可知,G/H是A群.因此G/H是全可置换群.
定理2.3设G是一个有限p群,p>2,|G/Φ(G)|=pd,G=〈a1,a2,···,ad〉,T=〈a,b〉,其中a,b∈{a1,a2,···,ad}.
若G是B群,则T为下列群之一:
(1)Mp(1,1,1);(2)Cpm×Cpn;(3)非交换亚循环群.
证明若T交换,由d(T)=2可知:即定理中的(2).以下设T非交换.取H 情形1交换 则可以设 其中1≤i,j,k≤p. 此时讨论参数n: 因此ab∈K〈a〉. 另一方面,ab=bac̸∈〈b〉〈a〉⊇K〈a〉.这与ab∈K〈a〉矛盾. 情形2不交换 其中参数r,s,u,t是非负整数且满足r≥1,u≤r.设T=〈a,b〉. 则可以设 其中1≤i,j,k≤p. 子情形1i̸=p 由T′=〈[a,b],T3〉,通过计算容易得到,T′=〈aprxk〉,即T′循环.因为不交换,所以r+s+u>r.因此可以得到x∈T′. 若x̸∈ʊ1(T′),由T′循环可知T′=〈x〉.这与T′=〉矛盾.因此有 子情形2i=p 此时 若j̸=p时,则 显然〈a〉〈b〉⊆T.因此T=〈a〉〈b〉.故T亚循环.得到定理中(3)的一部分.因此总有j=p.此时 若k=p,则d(T)̸=2.矛盾.所以总有k̸=p.用xk替换x,有 通过计算容易得到apr+s+u−1∈Z(G). 令K=〈apr+s+u−1〉×〈b〉,则|K|≥p2.由〈a〉̸⊆(G),则〈a〉K=K〈a〉.因此ab∈K〈a〉. 另一方面, 这与〈a〉K=K〈a〉矛盾.因此没有得到符合条件的群. 推论2.1设G是一个有限p群,p>2,|G/Φ(G)|=pd,G=〈a1,a2,···,ad〉,T=〈a,b〉,其中a,b∈{a1,a2,···,ad}. (1)若G是B群,则T也是B群. (2)设T1≤T,T2≤T,|T2|̸=p.若G是B群,则T1T2=T2T1. 证明(1)由定理3可知,TMp(1,1,1)或者T为一个亚循环群.亚循环群都是A群,因此都是B群. 只需验证Mp(1,1,1)是B群.∀K≤T且|K|̸=p,则有KT.由B群定义可知, Mp(1,1,1)是B群.即T是B群. 推论2.2设G是一个有限p群,p>2.G是二元生成的B群当且仅当G为下列群之一: (1)Mp(1,1,1);(2)Cpm×Cpn;(3)非交换亚循环群. 证明(⇒)由定理3直接推出. (⇐)只需对定理中的群一一验证是B群.证明过程同推论4的证明. 推论2.3设G是一个有限p群,p>2,G是二元生成的B群.若H≤G,则H是一个B群. 证明只需对推论5中的群进行验证.注意到亚循环群的子群都是亚循环群即可得到结论. [1]Kirtland J.Finite groups with all subgroups not contained in the Frattini subgroup permutable[J].Arch. Math.,2011,97:399-406. [2]Iwasawa K.Uber die endlichen Gruppen und die Verba nde ihrer Untergruppen[J].Fac.Sci.Imp.Tokyo Sect.,1941,14:171-199. [3]徐明曜.有限群导引(上册)[M].2版.北京:科学出版社,1999. [4]徐明曜,曲海鹏.有限p群[M].北京:北京大学出版社,2010. Some groups with a good permutability of subgroups Zhong Yanlin1,Zeng Jiwen2 The paper studies the in fl uence of subgroups replacement properties on the structure of fi nite groups. A fi nite group is derived from the subgroup replacement properties,which is called B group.B groups is the extension of full permutation groups,the power of p center expansion of full permutation groups and Subgroups order use to get some properties of B groups and descriptions about the structure of B groups.By using the structure of B group,we get the necessary and sufficient conditions of a fi nite p(p>2)group being a binary generating B group. fi nite groups,B groups, fi nite p groups O152 A 1008-5513(2014)05-0491-05 10.3969/j.issn.1008-5513.2014.05.009 2014-06-10. 福建省中青年教师教育科研项目(JB14108);福建省自然科学基金(2012J01022). 钟艳林(1980-),硕士,讲师,研究方向:有限群论及p群. 2010 MSC:20B05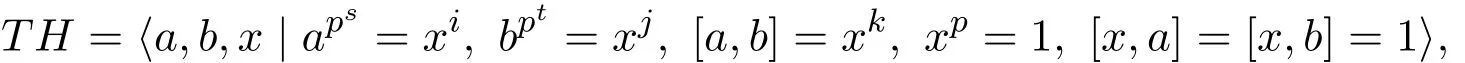




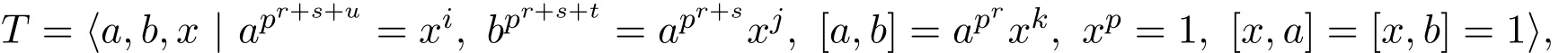

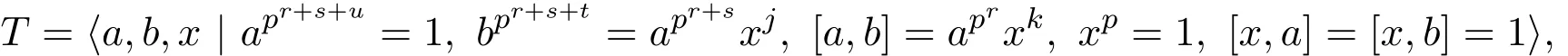




(1.Information Management Department,Minnan University of Science and Technology, Quanzhou362700,China; 2.School of Mathematical Science,Xiamen University,Xiamen361005,China)
