Diestel-Faires定理在局部凸空间中的推广

乌仁其其格,杨梅荣

(内蒙古赤峰学院数学与统计学院,内蒙古赤峰024000)

Diestel-Faires定理在局部凸空间中的推广

乌仁其其格,杨梅荣

(内蒙古赤峰学院数学与统计学院,内蒙古赤峰024000)

通过Banach空间与局部凸空间的对比,将Banach空间上的Diestel-Faires定理在局部凸空间上进行推广.进一步给出了局部凸空间上的Orlicz-Pettis定理与推论.

局部凸空间;lcs空间;Diestel-Faires定理;Orlicz-Pettis定理

1 预备知识

设X是实数域或复数域K上的向量空间,P是X上一族半范数,满足其中p−1(0)={x∈X:p(x)=0},这样的半范数族P常称为分离的[1-4].令σP是半范数族P生成的X上的局部凸拓扑[5],则它是局部凸分离向量空间,简记为lcs[6].

用X∗≡(X,σP)∗表示(X,σP)的拓扑对偶空间,并对每个p∈P考虑X∗的向量子空间

对任意的x∗∈X∗(p),定义∥x∗∥p=|X∗(x)|,则∥·∥p是X∗(p)上的范数,并用B(X∗(p))表示X∗(p)中的单位闭球,实际上(X∗(p),∥·∥)正是半范空间(X,p)的拓扑对偶空间(X,p)∗.

设Ω是某个取定的集,有时也称为基∪本空间.以Ω的某些子集为元素作成的集如果满足Ω∈,且对任何E1,E2∈都有E1E2∈E1E2∈,则称为Ω上的域.进一步,如果对任何一列{Ei}⊂都有就称域F是Ω上的σ-域.

2 主要结论

定理2.1(Diestel-Faires)[7]设X是Banach空间,F是由Ω的子集作成的域,G:→X是有界向量测度,若G不是强可加的,则存在(在内)拓扑同构T:c0→X和互不相交集列En⊂,使对任意自然数n,T(en)=G(En),从而c0中每一个0,1值序列的T-象是包含在G()中.若F是一个σ-域,将c0换成l∞结论仍成立.其中en表示第n项为1,其它项为0的数列.

以下是Diestel-Faires定理2.1在lcs空间中的推广.

定理2.2设(X,σP)是p-完备的lcs空间,是由Ω的子集作成的域,G:→X是有界向量测度:

(1)若G不是强可加的,则存在p0∈P(在内)拓扑同构T:c0→(X,p0)和互不相交集列{En}⊂,使得对每个自然数n,p0[T(en)−G(En)]=0成立,从而c0中每一个0,1值序列的T-像包含在G(F)+中.

(2)若F是σ-域,将(1)中的c0换成l∞结论仍成立.

证明(1)设F是域,因为G有界但不是强可加的,所以存在互不相交集列{An}⊂F,使得G(An)↛0(依σP拓扑),这样存在p0∈P,使得当n→∞时,p0[G(An)]↛0.如前, π表示从半范空间(X,p0)到商空间(∥·∥p0)的商映射,由于π是连续线性映射,从而πG:−→,∥·∥p0)是有界向量测度.

再由商映射π是等半范的,进一步可知πG不是强可加的向量测度,因(X,σP)是p-完备的lcs空间,知(X,p0)是完备的半范空间,故∥·∥p0)是Banach空间,根据Diestel-Faires定理2.1,存在(在内)拓扑同构S:c0→和互不相交集列{En}⊂,使得对每个自然数n,S(en)=πG(En).

取定X关于半范数p0的零空间的代数补线性子空间Y,则商映射π在Y上的限制π|Y:Y→是在上等距同构映射,其逆映射(π|Y)−1:Y也是在上等距同构映射.令T=(π|Y)−1·S,则T是从c0到(X,p0)的(在内)拓扑同构映射,且对任意的自然数n,有

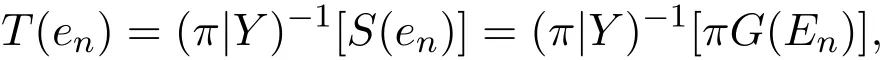
即

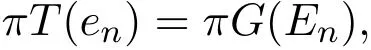
则

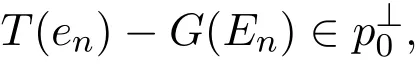
从而

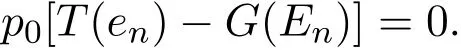
(2)将(1)中的域F换为σ域,c0换为l∞,类似可证.

推论2.1设(X,σP)是p-完备的lcs空间,是由Ω的子集作成的域,是有界向量测度,则G是强可加的当且仅当对任意的p∈P和任意渐张集列在(X,p)中弱收敛.

证明必要性:若G是强可加的,任意的渐张集列极限在拓扑σP下存在,所以对任意的在中收敛,进而在(X,p)中弱收敛.

充分性:用反证法证明.假设G不强可加,由于(X,σP)是p-完备的,据定理2.2知,存在p0∈P,在内拓扑同构和互不相交集列使得对任意的有如前所设π是半范空间(X,p0)关于零子空间的商映射,令S =πT,则是在内拓扑同构,且对任意的有

若不然存在x0∈X,使得{G(Em)}在(X,p0)中弱收敛于x0.因为π是弱-弱连续的,所以依的弱拓扑收敛于对任意的

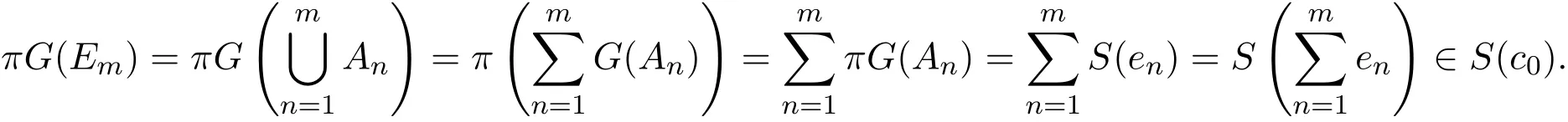
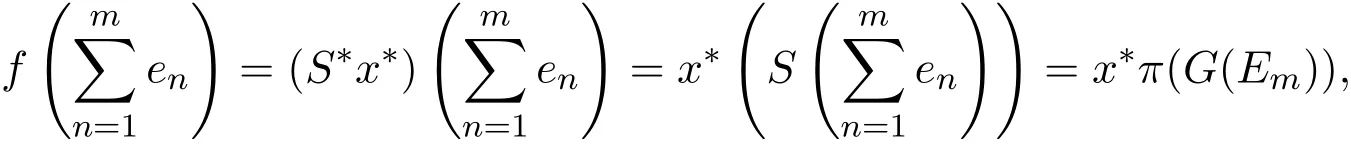
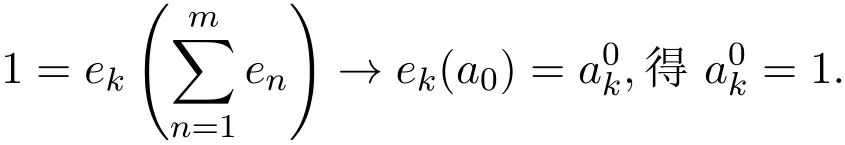
所以a0=(1,1,···,1,···)∈c0,矛盾.

定理2.3 (Orlicz-pettis)[7]设是Banach空间X中一个形式级数,且任何一个子级数都是弱收敛的,则按范数无条件收敛.

以下是Orlicz-Pettis定理2.3在lcs空间中的推广.

定理2.4设(X,σP)是p-完备的lcs空间,是X中一个形式级数,对任意的p∈P,在半范空间(X,p)中任何子级数都弱收敛,则依拓扑σP无条件收敛.

证明设X中的级数对任意的p∈P在(X,p)中任何子级数弱收敛,可知对任意的x∗∈(X,p)∗都有定义

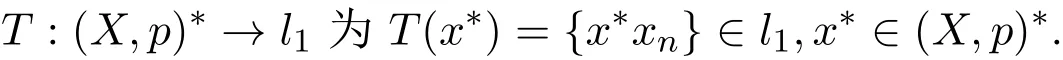
由闭图定理[8]可证T是有界线性算子,从而

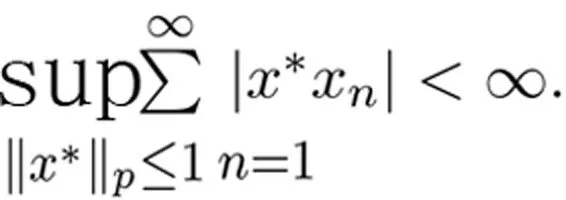
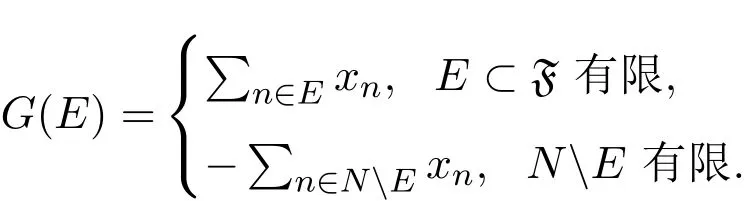
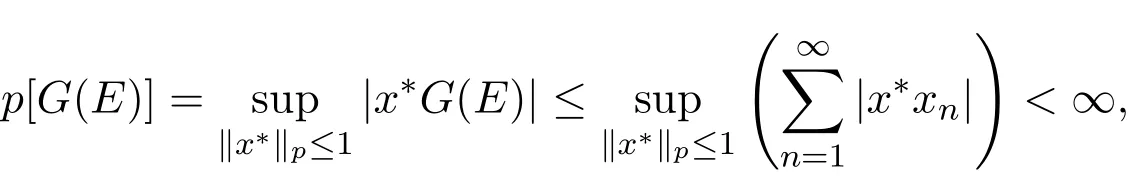
所以G是有界向量测度.任意的p∈P,{G(En)}在(X,p)中弱收敛.

设{En}是中渐张集列,若是最终非常集列,则每个En是有限的,此时{G(En)}是重排后的某个子级数部分和序列,因为数域K中任何无穷级数,子级数收敛,所以对

若{En}是最终常集列,显然{G(En)}在(X,p)中是收敛的.这样,对任意的p∈P,对中任意渐张集列中是弱收敛的.由(X,σP)是p-完备,据推论2.1得G是强可加的,故依拓扑σP无条件收敛.

[1] 孙立民.取值于局部凸空间矢值测度的几个性质[J].哈尔滨师范大学自然科学学报,1996,12:16-19.

[2] 武立中,孙立民.局部凸空间上矢值测度某些有界变差的等价性[J].哈尔滨工业大学自然科学学报,1995,27:5-7.

[3] 施慧华.向量值测度的泛函表示[J].厦门大学学报:自然科学版,2013,3:306-308.

[4] 滕岩梅.某种局部凸空间上的Bishop-phelps定理[J].数学学报,2005,4:781-784.

[5] 陈利国.关于局部凸空间的中点局部一致凸性[J].纯粹数学与应用数学,2011,6:749-755.

[6] Halmos P R.Measure Theorey[M].New York:Springer-verlag,1974.

[7] Joseph.Diestl,John Jerry Uhl.Vector Measures[M].Providence:Math.Surveys,Am.Math.Soc.,1977.

[8] Taylor A E.Introduction to Functional Analysis[M].NewYork:John Wileysons,1958.

Generalization of Diestel-Faires theorem on locally convex spaces

Wurenqiqige,Yang Meirong
(College of Mathematics and Statistics,Chifeng University,Chifeng 024000,China)

By contrasting Banach space and locally convex spaces,we promote Diestel-Faires theorem to locally convex space,and put up with Orlicz-Pettis theorem of locally convex spaces and the deduction of the Diestel-Faires theorem.

locally convex space,lcs space,Diestel-Faires theorem,Orlicz-Pettis theorem

O177.99

A

1008-5513(2014)05-0503-04

10.3969/j.issn.1008-5513.2014.05.011

2014-01-21.

乌仁其其格(1979-),硕士,讲师,研究方向：泛函分析.

2010 MSC:47A62