概率度量空间中广义β-可容许映射的二元重合点定理及其应用

徐文清,朱传喜

(南昌大学数学系,江西南昌330031)

概率度量空间中广义β-可容许映射的二元重合点定理及其应用

徐文清,朱传喜

(南昌大学数学系,江西南昌330031)

在Menger PM-空间中,引入广义β-可容许映射的概念.在不要求两映射可交换的情况下,利用迭代法,建立了广义β-可容许映射的二元重合点定理.获得了一些新的结果,推广和改进了相关文献中的不动点定理和二元重合点定理.最后,给出了主要结果的一个应用.

Menger PM-空间;二元重合点;β-可容许映射;相容映射

1 引言与预备知识

1942年,文献[1]中首次提出概率度量空间,其中概率度量空间中的不动点理论已成为概率分析的重要内容之一,也是数学研究领域比较活跃的一部分.许多作者已经得到了概率度量空间中不同压缩条件下的不动点定理[2-10].

近年来,有关序度量空间、概率度量空间中映射的二元重合点理论的研究也比较活跃.例如,2009年,文献[11]获得序度量空间中g-混合单调映射的二元重合点定理.2011年,文献[12]得到了半序概率度量空间中可交换映射在压缩条件下的二元重合点定理.2013年,文献[13]在半序概率度量空间中定义了相容映射,同时建立了该映射在不满足可交换条件下的二元重合点定理,从而推广了文献[12]中的相关定理.度量空间中的重合点定理或不动点定理可参考文献[14-15].

最近,文献[16]在概率度量空间中定义了β-可容许映射,并得到了该空间中β-可容许映射的不动点定理.本文在Menger PM-空间中,引入广义β-可容许映射的概念.在不要求两映射可交换的情况下,建立了广义β-可容许映射的二元重合点定理.所得结果推广了文献[12-13,16]中的不动点定理和二元重合点定理.最后,给出了主要结果的一个应用.

为方便起见,首先回顾一些基本概念和引理[2].

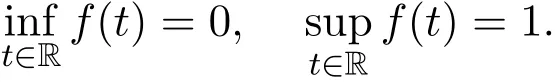
用D表示一切分布函数的集合,D+={F:F∈D,F(t)=0,∀t≤0},并用H(t)表示一特殊分布函数,其定义如下:

映像∆:[0,1]2→[0,1]称为三角范数(简称为t-范数),如果它满足如下条件:对任意a,b,c,d∈[0,1],有

(∆1)∆(a,1)=a,∆(0,0)=0;(∆2)∆(a,b)=∆(b,a);

(∆3)∆(a,b)≤∆(c,d),∀c≥a,d≥b;(∆4)∆(∆(a,b),c)=∆(a,∆(b,c)).

设∆M(a,b)=min{a,b},∆p(a,b)=ab,∆m(a,b)={a+b−1,0},显然它们为t-范数.

(X,F,∆)称为Menger PM-空间,如果X是一抽象集,∆为t-范数,F是X×X到D+的映象(记分布函数F(x,y)为Fx,y,而Fx,y(t)表示Fx,y在t∈R的值),满足下面的条件:

(PM1)Fx,y(0)=0;

(PM2)Fx,y(t)=H(t),∀t∈当且仅当x=y;

(PM3)Fx,y(t)=Fy,x(t);

(PM4)(Menger三角不等式)对任意x,y,z∈X,t1,t2∈,有

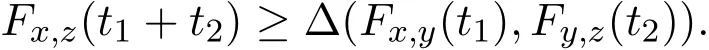
定义1.1[4]设Φ={ϕ:[0,1]→[0,1]}为一个函数类,其中函数ϕ满足如下条件:

(i)ϕ(t)=0当且仅当t=0;(ii)ϕ是严格增的且当t→∞时,ϕ(t)→∞;

(iii)ϕ在(0,∞)上是左连续的;(iv)ϕ在t=0处连续.

定义1.2[11]设X为一非空集合,G:X×X→X和g:X→X是X上的两自映射,元素(x,y)∈X×X称为G的二元不动点,如果G(x,y)=x和G(y,x)=y.元素(x,y)∈X×X称为G和g的二元重合点,如果G(x,y)=g(x)和G(y,x)=g(y).

定义1.3[16]设(X,F,∆)是一Menger PM-空间,β:X×X×(0,∞)→(0,∞)是一函数且g:X→X是X上的自映射,称g是β-可容许的,如果存在x,y∈X,使得对任意t>0, β(x,y,t)≤1,则β(g(x),g(y),t)≤1,∀t>0.

注1.1β-可容许映射不一定是单调映射;反之,单调映射也不一定是β-可容许映射.另外,β函数不一定可传递(称β是传递的,如果x,y,z∈X对任意t>0,β(x,y,t)≤1, β(y,z,t)≤1,则β(x,z,t)≤1).

例1.1设X=[0,∞),f:X→X,g:X→X,β:X×X×(0,∞)→(0,∞)定义如下:

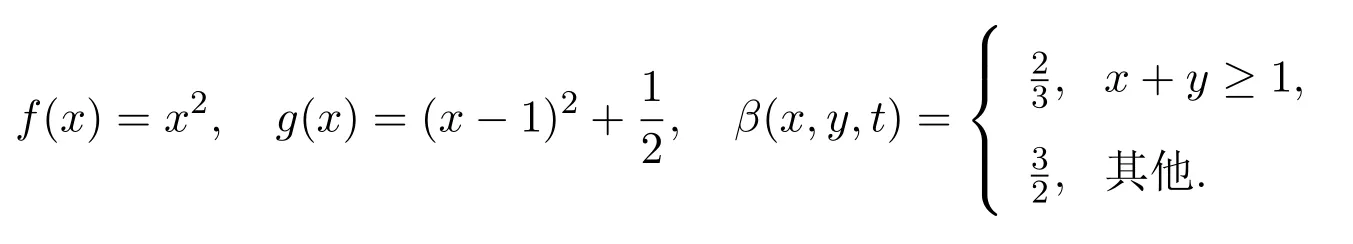
事实上,函数f在X上是不减的,若β(x,y,t)≤1,则x+y≥1.但x2+y2不一定大于1,因此,f不是β-可容许的.若β(x,y,t)≤1,则故g是β-可容许的,但很显然g在X上不是单调的.由β的定义可知,由均值不等式可知,但因此,β不是可传递的.

定义1.4[13]设(X,F,∆)是一完备的Menger PM-空间,G:X×X→X和g:X→X是X上的两自映射,G和g称为相容的,如果存在{xn}和{yn}为X中两个序列,x,y∈X,

则对任意t>0,有

引理1.1[5]设(X,F,∆)是一完备的Menger PM-空间,函数ϕ∈Φ,如果存在c∈(0,1),

2 主要结果

定义2.1设(X,F,∆)是Menger PM-空间,G:X×X→X和g:X→X是X上的两自映射且β:X×X×(0,∞)→(0,∞)是一函数,称G和g是广义β-可容许的,如果存在x,y,u,v∈X,使得对任意t>0,β(g(x),g(u),t)≤1和β(g(y),g(v),t)≤1,则

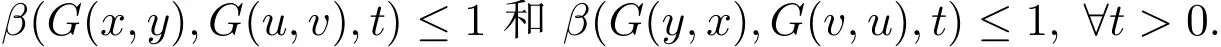
例2.1设X=[0,∞),g:X→X,G:X×X→X,β:X×X×(0,∞)→(0,∞)定义:

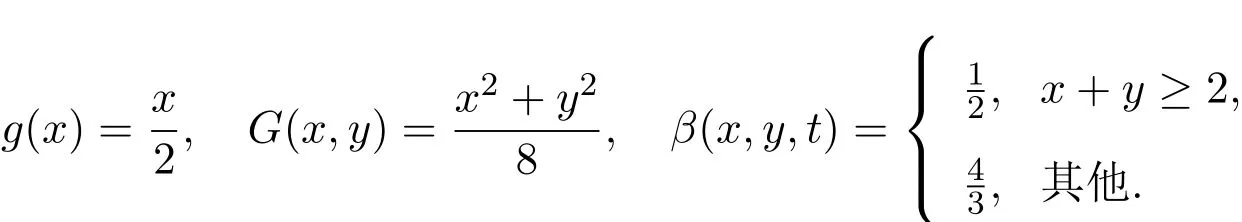
则G和g是广义β-可容许的.

若β(g(x),g(u),t)≤1,β(g(y),g(v),t)≤1,则

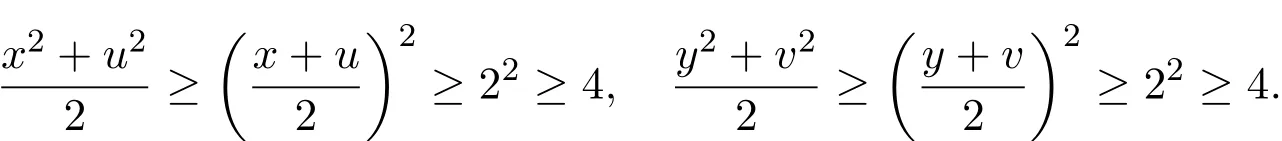
引理2.1设F∈D+,G1,G2,···,Gn:R→[0,1]都为不减函数,其中n∈Z+,如果存在ϕ∈Φ和c∈(0,1),使得对任意t>0,

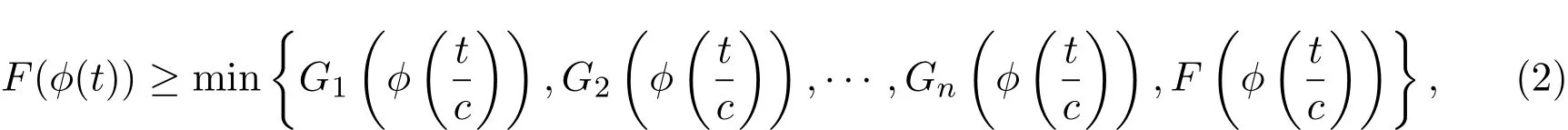
则

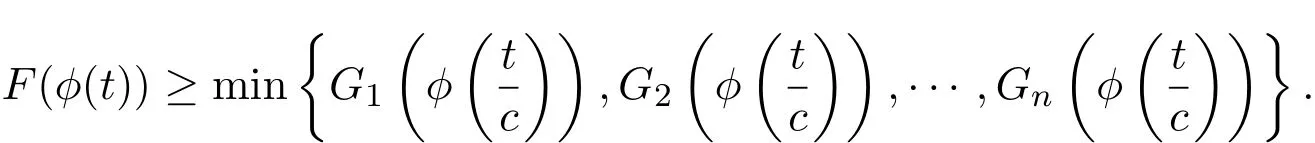
证明设G(t)=min{G1(ϕ(t)),G2(ϕ(t)),·(··,(Gn)()ϕ(t))}.

利用反证法证明.假设存在t0>0,使得Gϕt0>F(ϕ(t0)).由(1)式可知

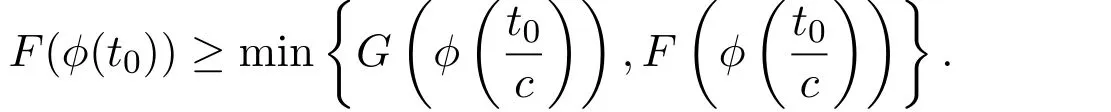
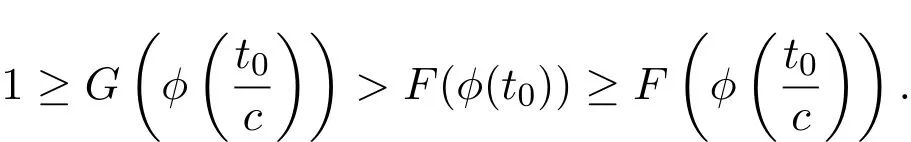
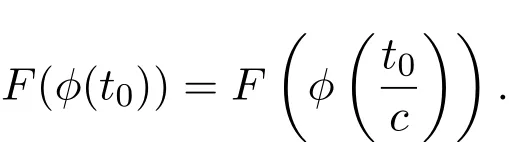
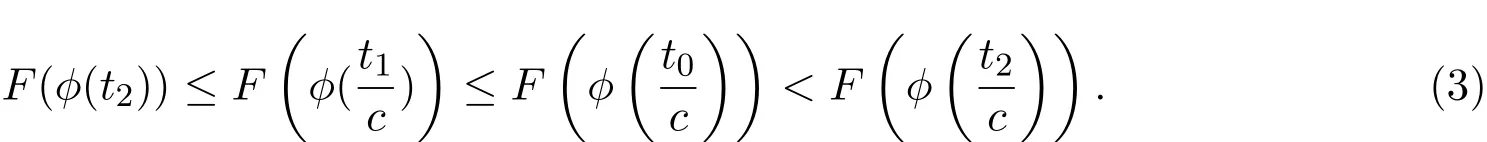
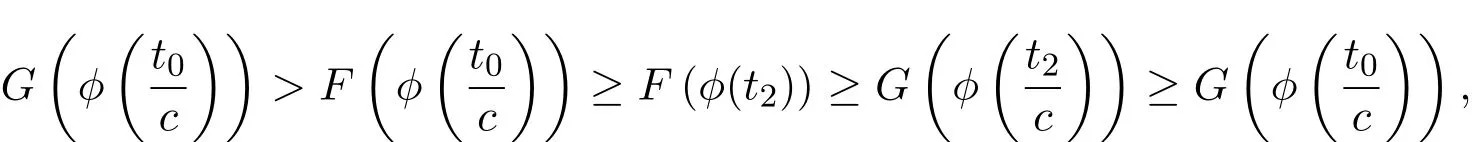
矛盾.因此假设不成立,结论成立.

引理2.2设(X,F,∆)是一Menger PM-空间,且ϕ∈Φ,如果存在c∈(0,1),x,y,u,v∈X,使得对任意t>0,有

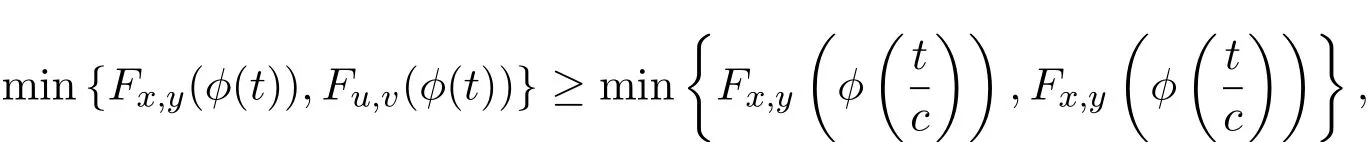
证明要证x=y和u=v,即证对任意t>0,min{Fx,y(t),Fu,v(t)}=1.利用反证法证明,假设存在t0>0,使得min{Fx,y(t0),Fu,v(t0)}<1.

由ϕ的性质可知,当t→∞时,ϕ(t)→∞.再由(X,F,∆)是一Menger PM-空间可得,当t→∞时,min{Fx,y(ϕ(t)),Fu,v(ϕ(t))}→1.因此存在t1>0,使得ϕ(t1)>t0且

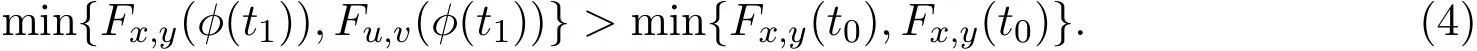
根据ϕ的性质,对t0>0,存在r>0使得t0>ϕ(r).由c∈(0,1),存在n∈N,使得r≥cnt1.由ϕ是严格增的可得t0>ϕ(cnt1).由已知条件可知:

这与(3)式矛盾.因此假设不成立,则x=y和u=v.

定理2.1设(X,F,∆)是完备的Menger PM-空间,∆为一连续的t-范数且∆(a,a)≥a,∀a∈[0,1].设β:X×X×(0,∞)→(0,∞)是一函数,函数ϕ∈,G:X×X→X和g:X→X是X上的两自映射且G和g是广义β-可容许的.如果存在c∈(0,1),对任意x,y,u,v∈X和t>0,有

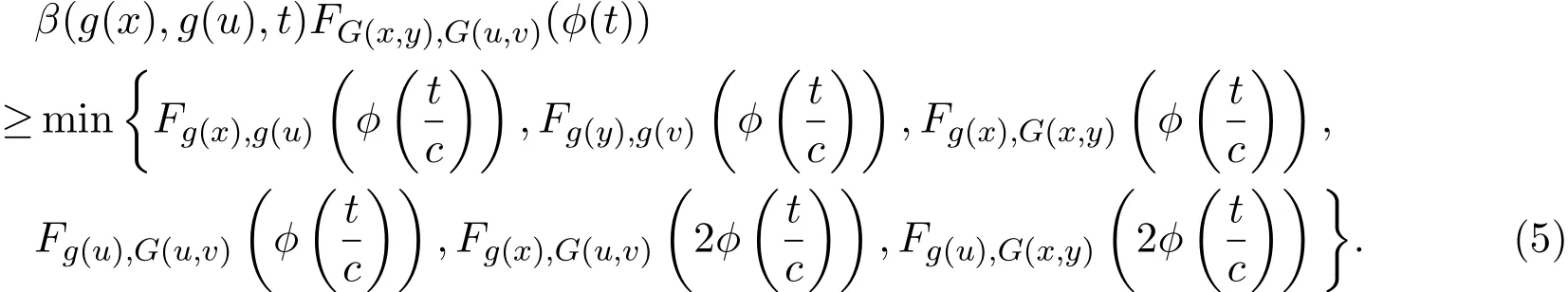
设G(X,X)⊂g(X),g是连续的,G和g是相容的,且满足下列条件之一:

(a)G是连续的;

(b)g是β-可容许的,如果序列{xn}⊂X使得对任意t>0,n∈N,β(xn,xn+1,t)≤1且xn→x,则对任意t>0,n∈N,β(xn,x,t)≤1.

存在x0,y0∈X使得对任意t>0,有

则存在x,y∈X使得G(x,y)=g(x)和G(y,x)=g(y),即(x,y)∈X×X为G和g的二元重合点.

证明由∆是连续的且对任意a∈[0,1],∆(a,a)≥a可知,∆(a,b)≥min{a,b}.因此由Menger三角不等式可知,对任意x,y∈X和t>0,有Fx,y(2t)≥min{Fx,z(t),Fz,y(t)}.

由已知条件可知,存在x0,y0∈X,使得

由G(X,X)⊂g(X)可知,存在x1,y1∈X,使得

再由G(X,X)⊂g(X)可知,存在x2,y2∈X,使得

依此类推可知存在点列{xn}和{yn},使得

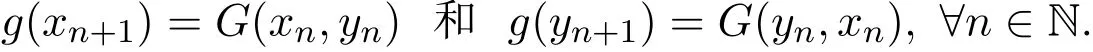
由G和g是广义β-可容许的,且β(g(x0),G(x0,y0),t)=β(g(x0),g(x1),t)≤1和β(g(y0),G(y0,x0),t)=β(g(y0),g(y1),t)≤1,则

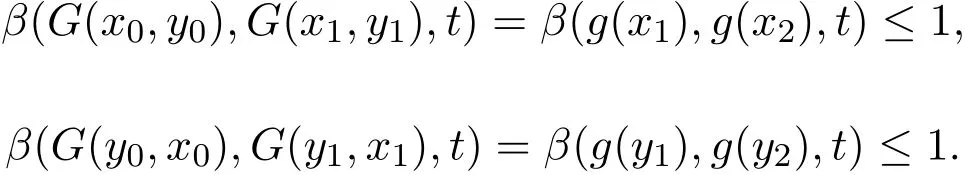
依此类推可知,对任意n∈N,t>0,

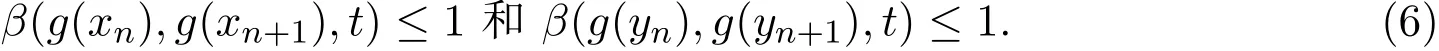
根据ϕ的性质,对任意t>0,存在r>0使得t>ϕ(r).由(4)式和(5)式可知

同理

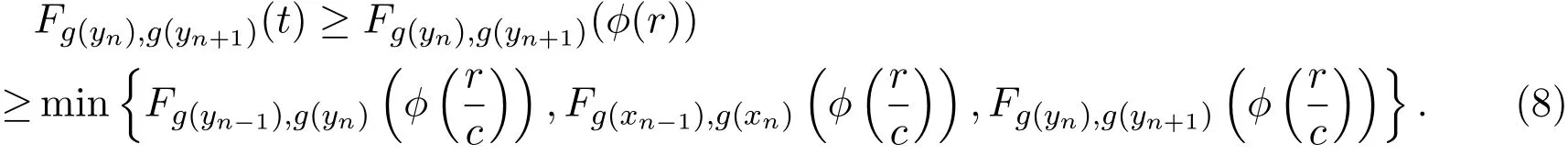
设Qn(t)=min{Fg(xn),g(xn+1)(t),Fg(yn),g(yn+1)(t)}.则Qn∈D+.结合(6)式和(7)式可得,

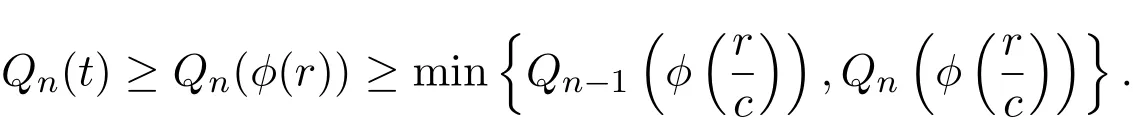
由引理2.1可知,

设m,n∈N,且m>n,由(8)式和∆≥∆M可知,

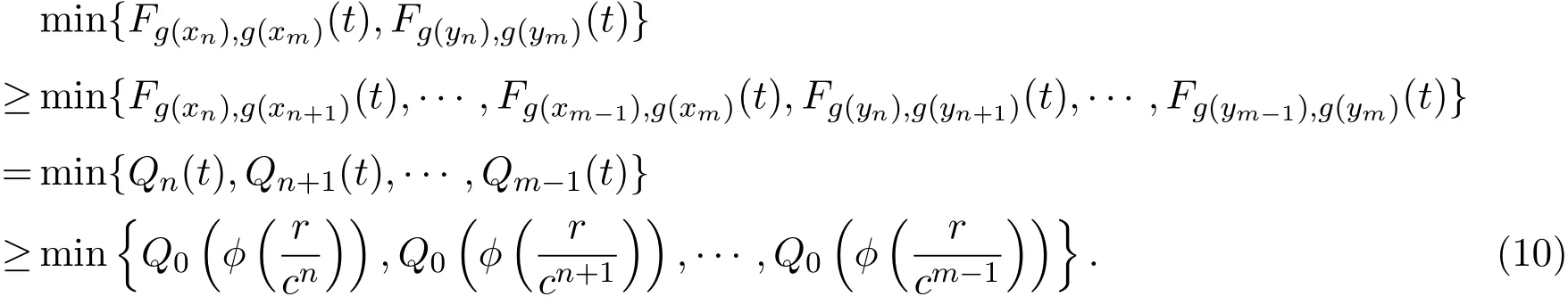
由ϕ是严增的,以及t→∞时,ϕ(t)→∞可知,对任给的ε∈(0,1),存在n0∈N,使得对任意n>n0,有

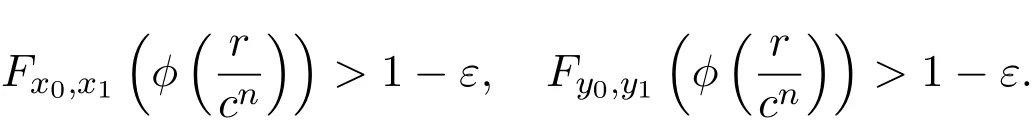
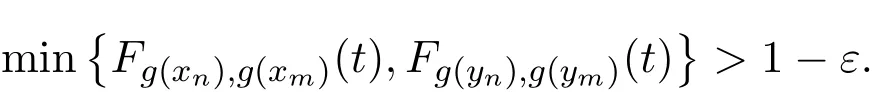
由ε>0和t>0的任意性可知,序列{g(xn)}和{g(yn)}是(X,F,∆)中的柯西列.由X的完备性,存在x,y∈X,使得

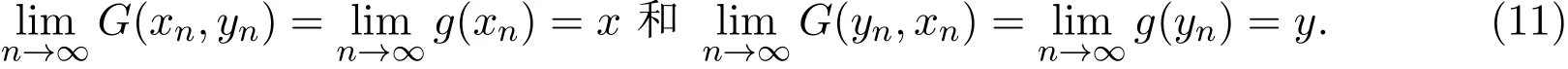
由g的连续性和(10)式可知,

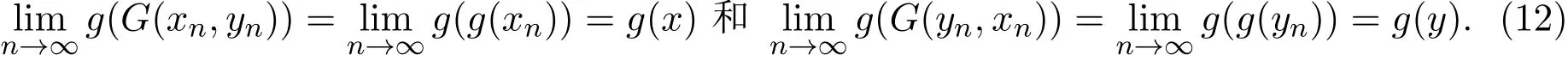
由G和g的相容性和(10)式可知,对任意t>0,

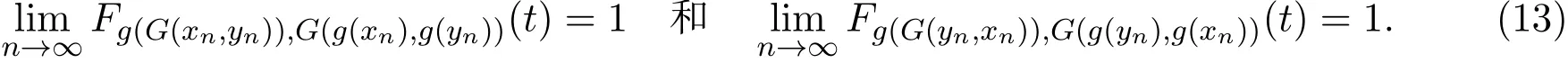
利用Menger三角不等式和∆≥∆M得,

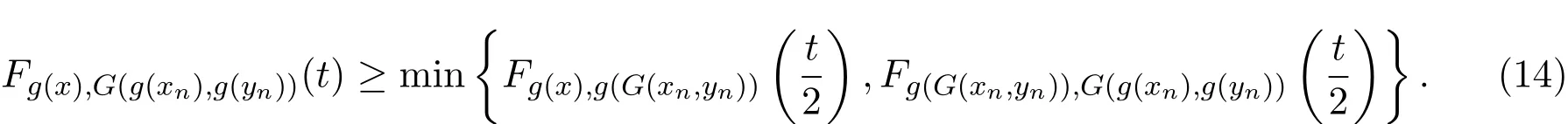
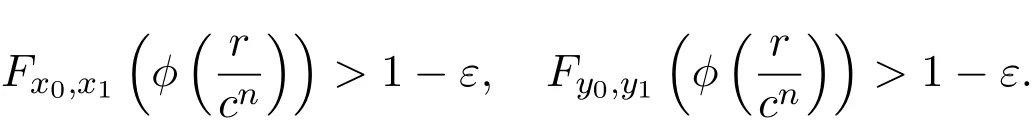
利用(11)式和(12)式,在(13)式中令n→∞可得,

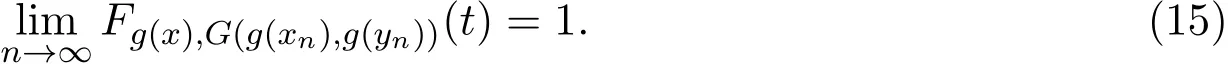
下证,G(x,y)=g(x)和G(y,x)=g(y).分两种情况证明:

(i)假设条件(a)成立,即G是连续的.由G的连续性和(10)式得

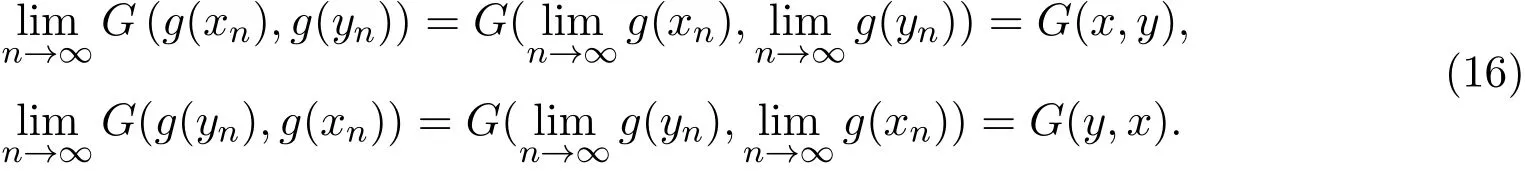
根据ϕ的性质,对任意t>0,存在r>0使得t>ϕ(r)>0.由Menger三角不等式和∆≥∆M可知,

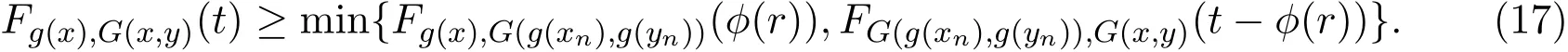
利用(14)-(15)式,在(16)式中左右两端取下极限可知,对任意的t>0,Fg(x),G(x,y)(t)≥1.则G(x,y)=g(x).同理,G(y,x)=g(y).

(ii)假设条件(b)成立.由ϕ严增性可知,对任意λ∈(0,1)和r>0,有ϕ(r)>ϕ(λr).由Menger三角不等式和∆≥∆M可知,

由(5)式,g(xn)→x和g(yn)→y可知,β(g(xn),x,t)≤1和β(g(yn),y,t)≤1.又由g是β-可容许的,则

由(4)式和∆≥∆M可知,

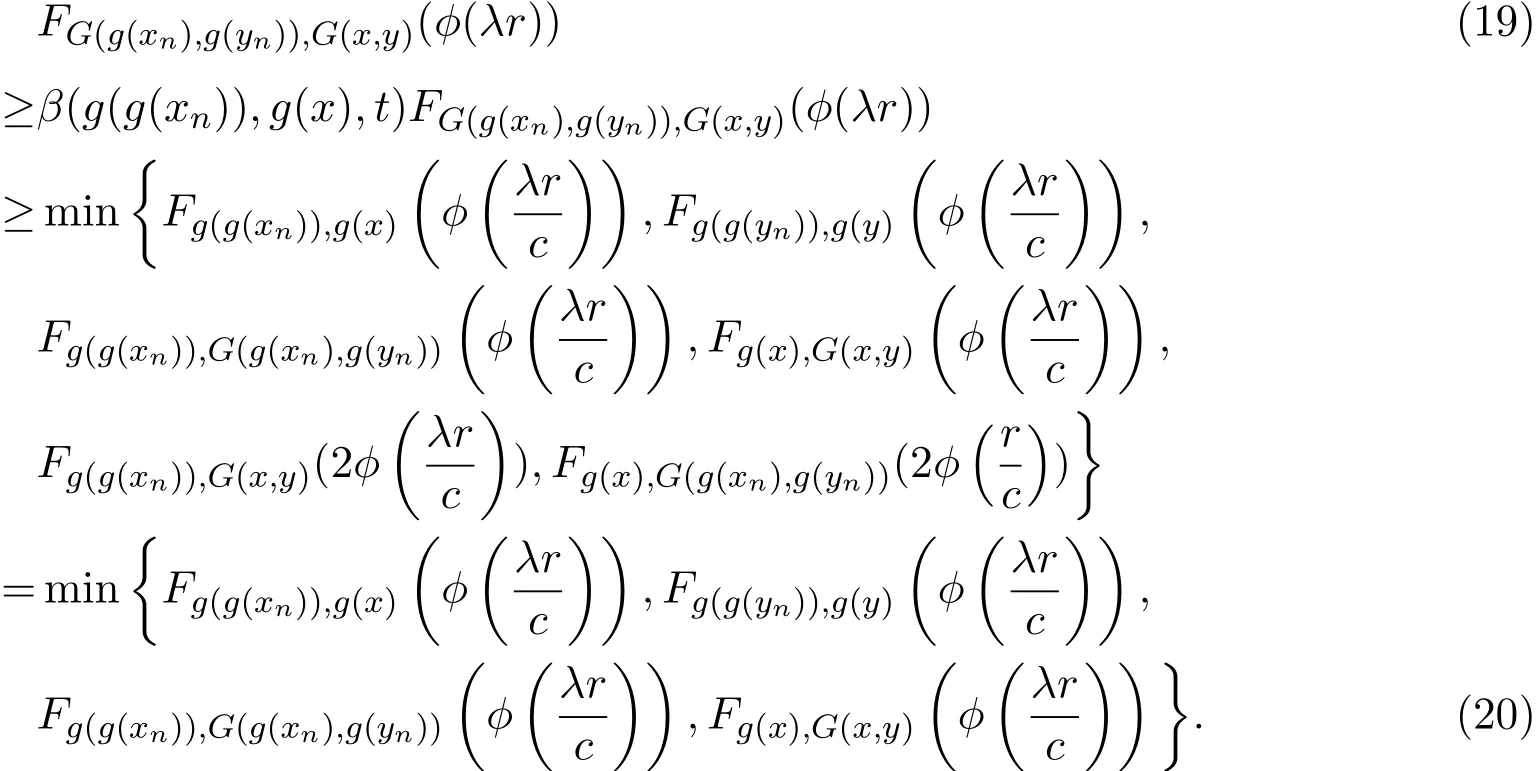
由Menger三角不等式和∆≥∆M可得,

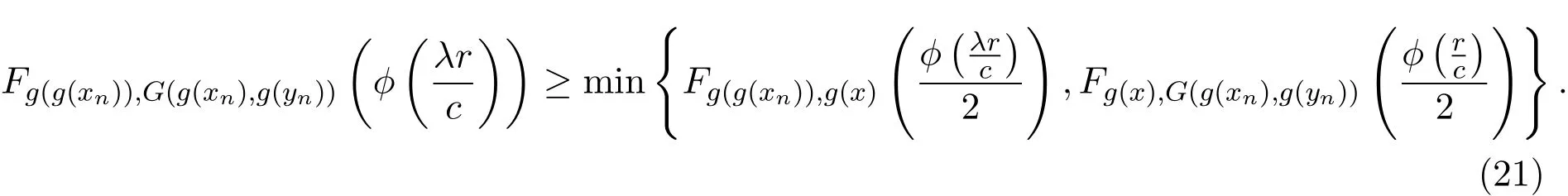
结合(17)-(19)式,可知

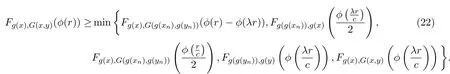
利用(11)式和(14)式,在(20)式中左右两端取下极限可知,对任意的r>0,有

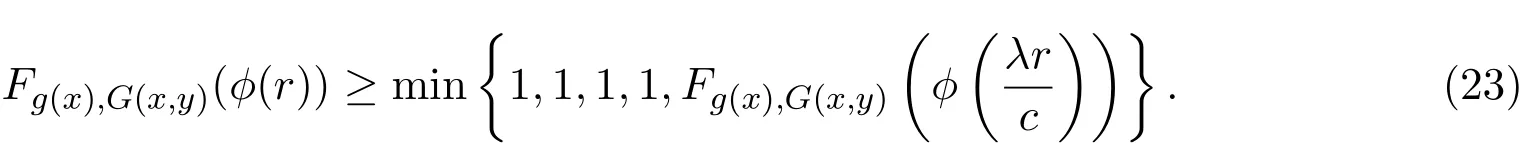
由ϕ是严格增且左连续的,F也是左连续的,在(21)式中令λ→1,可得

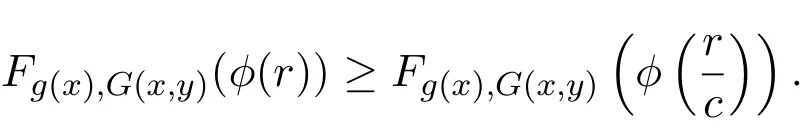
由引理1.1可知,G(x,y)=g(x).同理可证G(y,x)=g(y).

综上可知,存在x,y∈X,使得

即(x,y)∈X×X为G和g的二元重合点.

定理2.2假设在定理2.1中增加条件:(i)g是单射,(ii)对任意(x,y),(u,v)∈X×X,存在(z,w)∈X×X,使得对任意t>0,

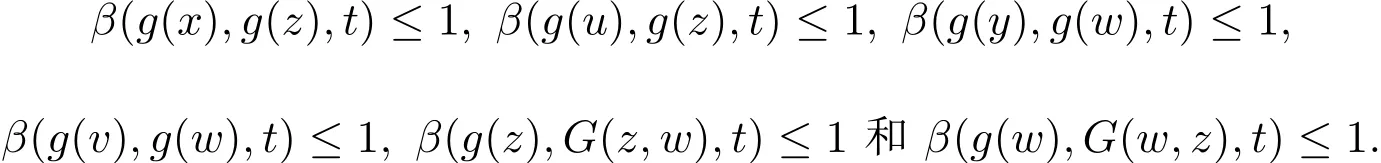
则G与g有唯一二元重合点.

证明由定理2.1可知,G与g存在二元重合点.下证重合点的唯一性,假设存在(x,y),(u,v)∈X×X,使得

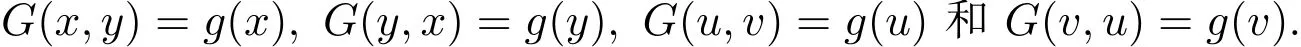
根据新增条件(ii),存在(z,w)∈X×X,使得对任意t>0,

β(g(x),g(z),t)≤1,β(g(u),g(z),t)≤1,β(g(y),g(w),t)≤1,

β(g(v),g(w),t)≤1,β(g(z),G(z,w),t)≤1和β(g(w),G(w,z),t)≤1.设z0=z和w0=w,由G(X×X)⊂g(X)可知,存在z1,w1∈X,使得

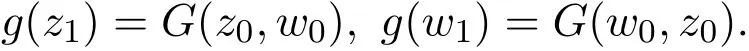
依次类推可知,存在X中两序列{g(zn)}和{g(wn)},使得

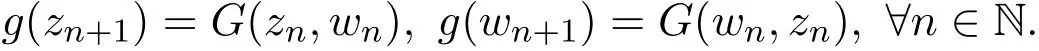
由β(g(x),g(z0),t)≤1,β(g(y),g(w0),t)≤1.再根据G和g是广义β-可容许的可得, β(G(x,y),G(z0,w0),t)=β(g(x),g(z1),t)≤1,β(G(y,x),G(w0,z0),t)=β(g(y),g(w1),t)≤1.依次类推可得,

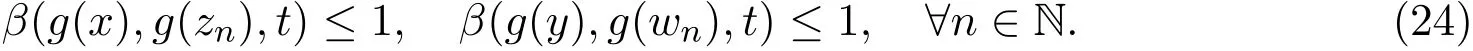
同理

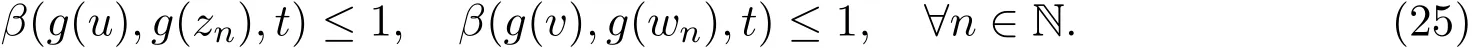
利用

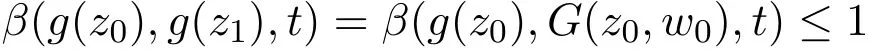
和

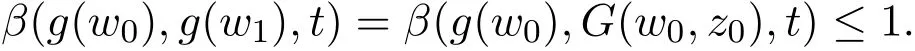
再根据G和g是广义β-可容许的,可得

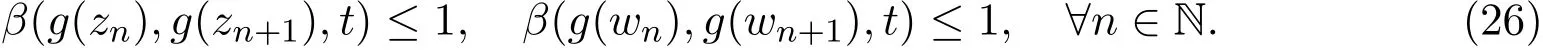
根据ϕ的性质,对任意t>0,存在r>0使得t>ϕ(r).由(4)式和(22)式可知,

同理

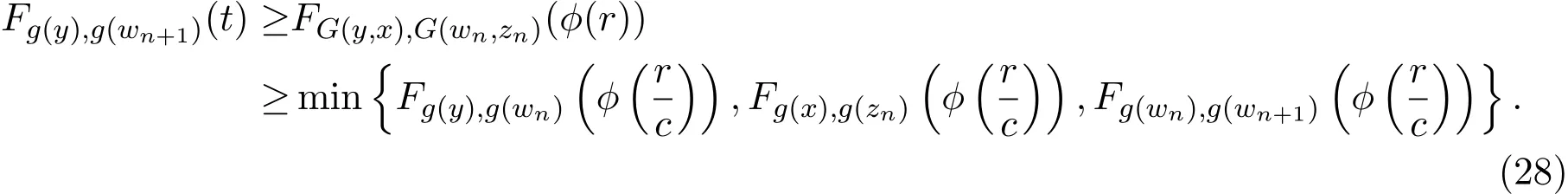
设

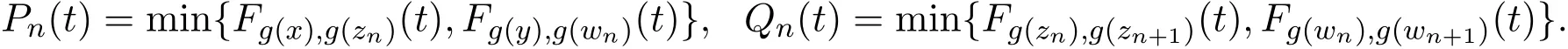
结合(25)式和(26)式,可得

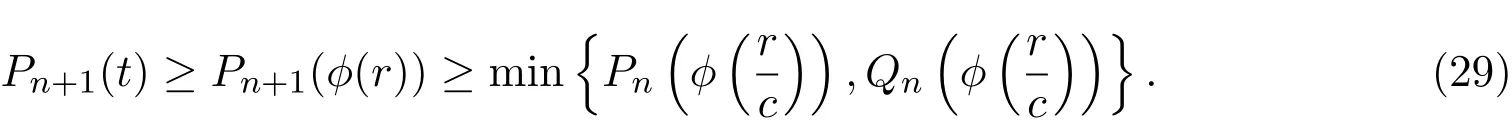
对(27)式分两种情况讨论:

证明可得,

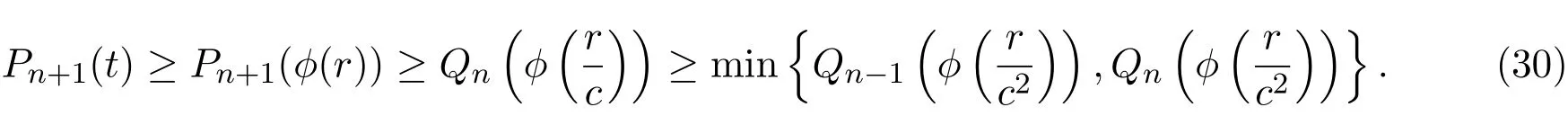
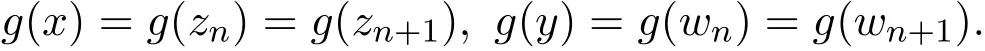
相应的也可得

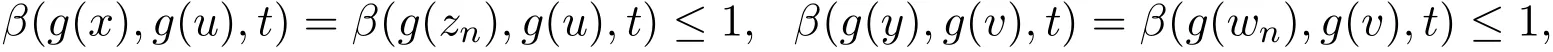
由(4)式可知,

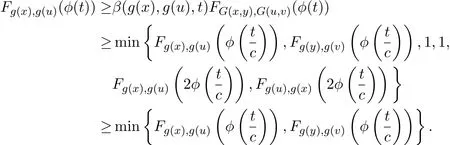
同理

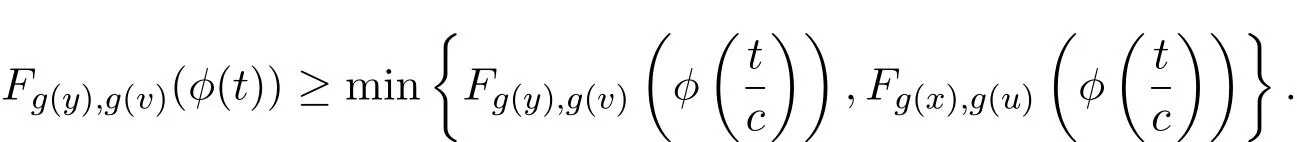
因此,

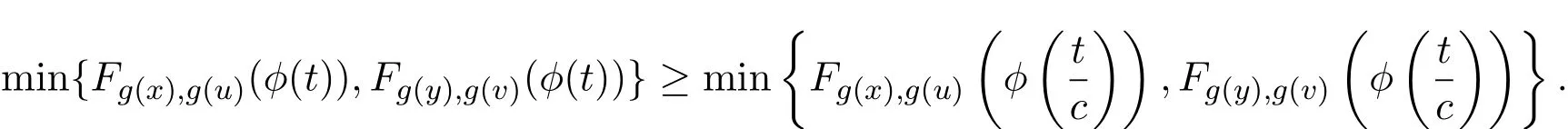
由引理2.2可知g(x)=g(u)和g(y)=g(v).

另一方面,若

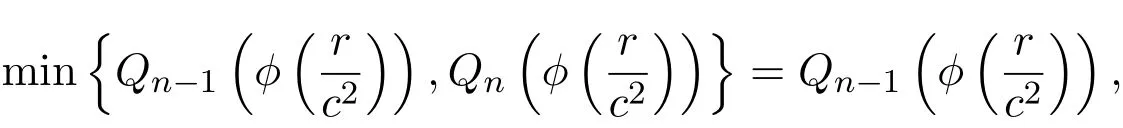
则由(28)式得

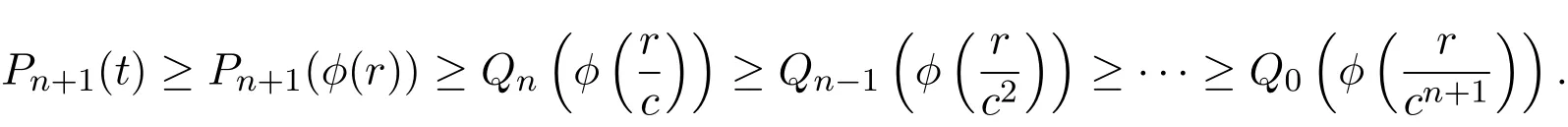
在上式中令n→∞得

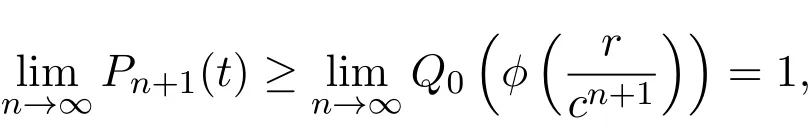
这表明g(zn)→g(x)和g(wn)→g(y).

2)假设

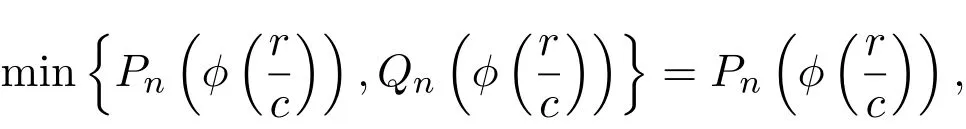
则由(27)式得

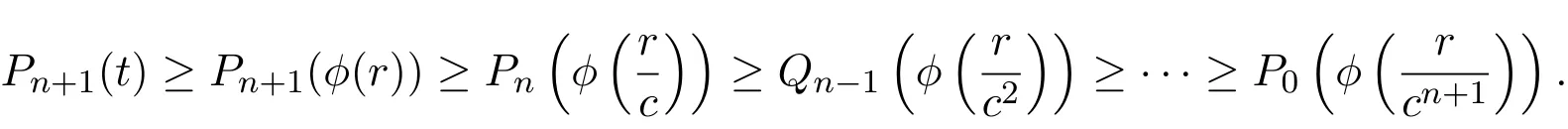
在上式中令n→∞得

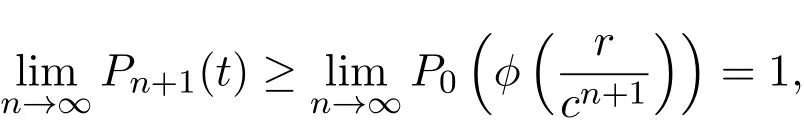
这也表明g(zn)→g(x)和g(wn)→g(y).

同理可得g(zn)→g(u)和g(wn)→g(v).由序列收敛的唯一性可知g(x)=g(u)和g(y)=g(v).再由g是单射可知x=u和y=v.因此唯一性得证.

3 应用

例3.1设x,y∈X,t>0,则(X,F,∆M)是完备的Menger PM-空间.

令g:X→X,G:X×X→X,ϕ:[0,1]→[0,1],β:X×X×(0,∞)→(0,∞)定义如下:

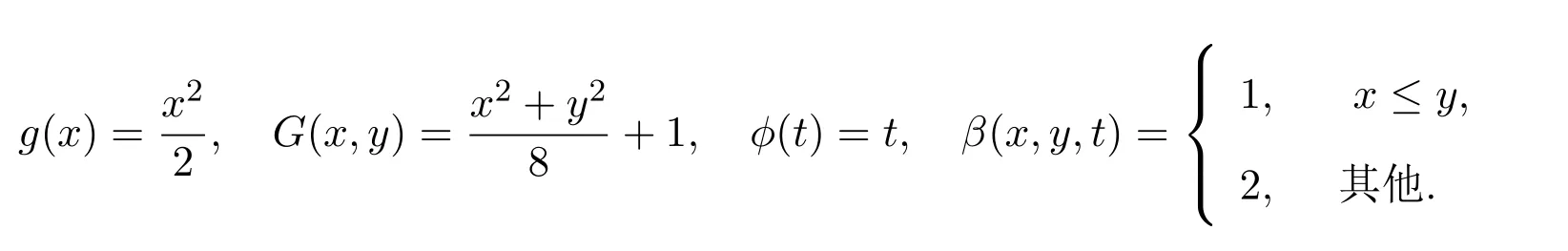
容易验证:G和g是连续的,G和g是β-可容许的,G(X×X)⊂g(X),ϕ∈Φ.设x0=1和y0=1,则

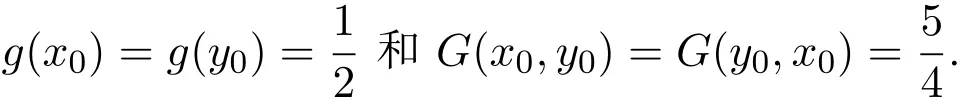
由β的定义可知,β(g(x0),G(x0,y0),t)≤1和β(g(y0),G(y0,x0),t)≤1,∀t>0.下证G和g是相容的.设{xn}和{yn}是X中的两序列,使得

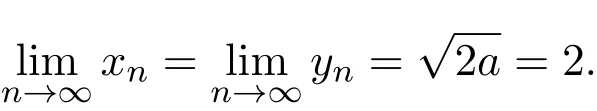
由G和g的连续性,可知

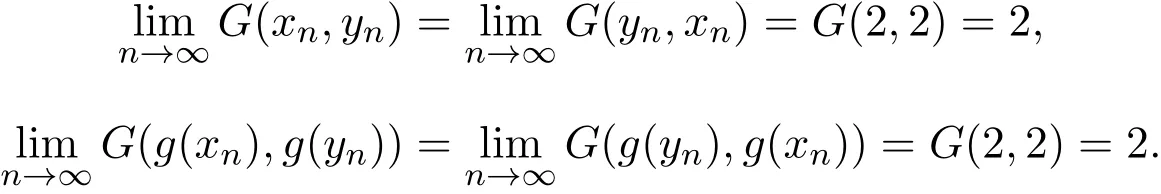
由Menger三角不等式和∆=∆M,可得

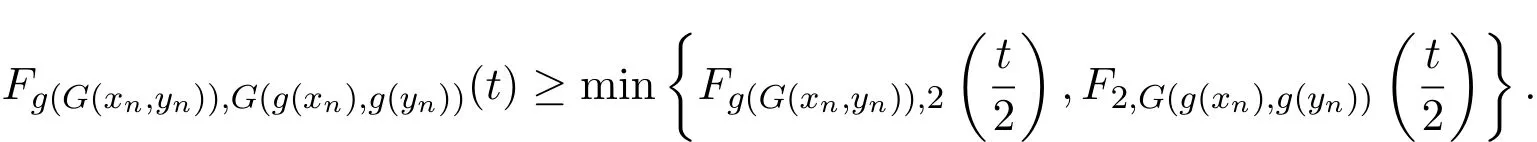
在上式中令n→∞,可得

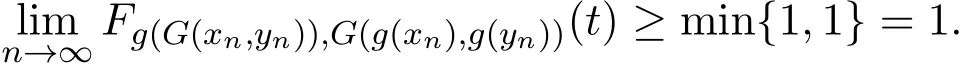
同理

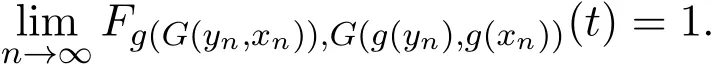
因此,G和g是相容的.

再由β的定义和(29)式可知,定理2.1的(4)成立.综上可知G,g,ϕ和β满足定理2.1的所有条件,所以G和g在X中存在二元重合点,由G(2,2)=g(2)=2,则x=2为G和g的二元不动点.

[1] Menger K.Statistical metrics[J].Proc.Nat.Acad.Sci.USA,1942,28:535-537.

[2] Chang S S,Cho Y J,Kang S M.Probabilistic Metric Spaces and Nonlinear Operator Theory[M].Chengdu: Sichuan University Press,1994.

[3] ´Ciri´c L.Solving the Banach fi xed point principle for nonlinear contractions in probabilistic metric spaces[J]. Nonlinear Anal.,2010,72:2009-2018.

[4]Choudhury B S,Das K P.A new contraction principle in Menger spaces[J].Acta.Math.Sin.(Engl.Ser)., 2012,6:257-264.

[5] Baba˘cev N A.Nonlinear generalized contraction on Menger PM-spaces[J].Appl.Anal.Discrete Math., 2008,23:1379-1386.

[6] Jachymski J.On probabilistic φ-contractions on Menger spaces[J].Nonlinear Anal.,2010,73:2199-2203.

[7] ´Ciri´c L,Mihet D,Saadati R.Monotone generalized contractions in partially ordered probabilistic metric spaces[J].Topology Appl.,2009,156:2838-2848.

[8] Fang J X,Gao Y.Common fi xed point theorems under strict contractive conditions in Menger spaces[J]. Nonlinear Anal.,2009,70:184-193.

[9] Fang J X.Common fi xed point theorems of compatible and weakly compatible maps in Menger spaces[J]. Nonlinear Anal.,2009,71:1833-1843.

[10] Xiao J Z,Zhu X H,Gao Y F.Common coupled fi xed point results for probabilistic φ-contractions in Menger spaces[J].Nonlinear Anal.,2011,74:4589-4600.

[11] Lakshmikantham V,´Ciri´c L.Coupled fi xed point theorems nonlinear contractions in partially ordered metric spaces[J].Nonlinear Anal.,2009,70:4341-4349.

[12] Hu X Q,Ma X Y.Coupled coincidence point theorems under contractive conditions in partially ordered probabilistic metric spaces[J].Nomlinear Anal.,2011,74:6451-6458.

[13] Dori´c D.Nonlinear coupled coincidence and coupled fi xed point theorems for not necessary commutative mappings in partially ordered probabilistic metric spaces[J].Appl.Math.Comput.,2013,219:5926-5935.

[14] 颜苏芊,刘加平,黄翔.一类新型混合单调算子的不动点定理及在工程科技中的应用[J].纯粹数学与应用数学, 2010,20(3):403-408.

[15] 卜香娟.Banach空间中一类序压缩映射的不动点定理[J].纯粹数学与应用数学,2012,28(3):334-341.

[16] Gopal D,Abbas M,Vetro C.Some new fi xed point theorems in Menger PM-spaces with application to Volterra type integral equation[J].Appl.Math.Comput.,2014,232:955-967.

Coupled coincidence point theorems for generalized β-admissible mappings in probabilistic metric spaces and its applications

Xu Wenqing,Zhu Chuanxi
(Department of Mathematics,Nanchang University,Nanchang330031,China)

In this paper,the new notion of generalized β-admissible mappings in Menger probabilistic metric spaces is introduced.We use the iterative method to establish some coupled coincidence point theorems for generalized β-admissible mappings in complete probabilistic metric spaces,where two mappings do not need to be commutative.Some new results are obtained,which generalize some fi xed point theorems and coupled coincidence point theorems in the recent corresponding literatures.Finally,an application is given to support our main results.

Menger probabilistic metric spaces,coupled coincidence point,β-admissible mappings, compatible mappings

O177.92

A

1008-5513(2014)05-0520-14

10.3969/j.issn.1008-5513.2014.05.014

2014-05-02.

国家自然科学基金(11361042,11071108,11461045);江西省自然科学基金(20132BAB201001,2010GZS0147).

徐文清(1989-),硕士生,研究方向:应用泛函分析.

2010 MSC:47H10