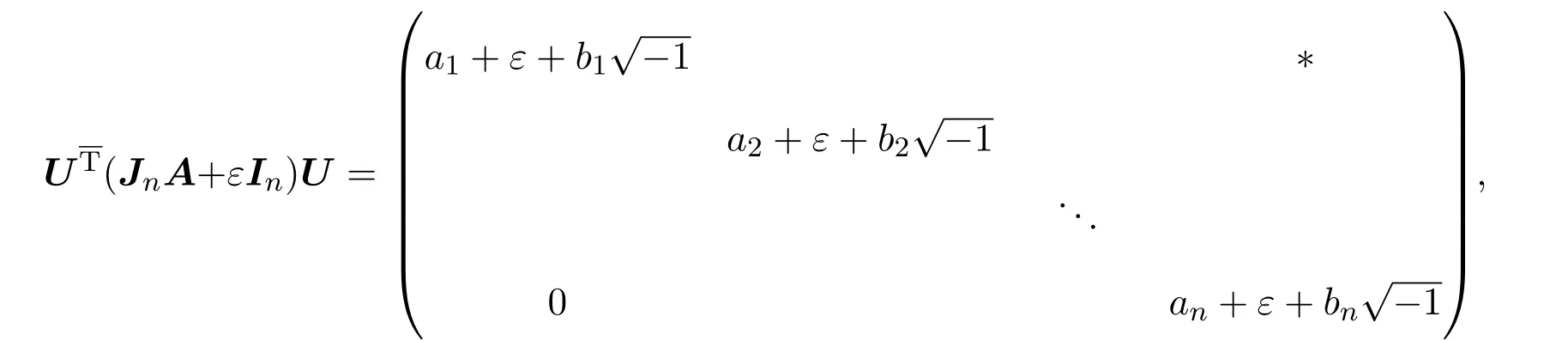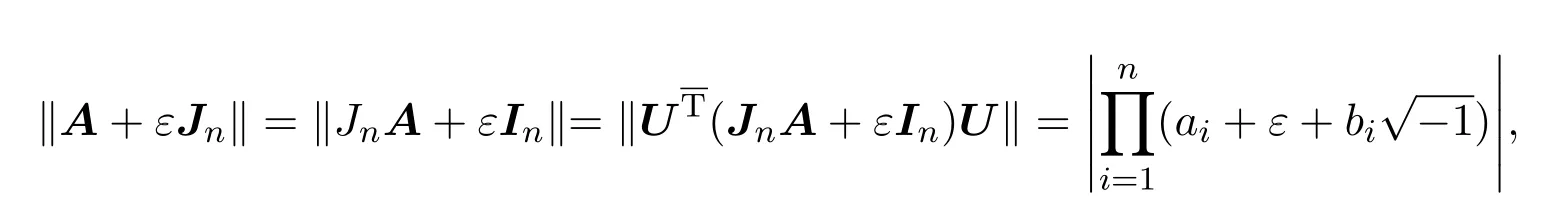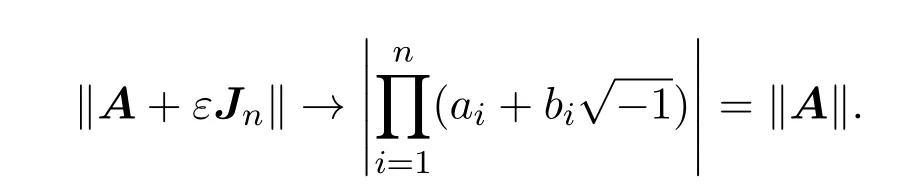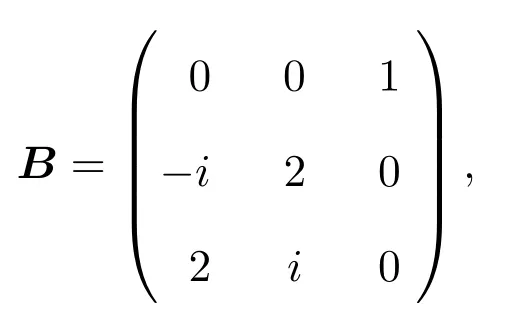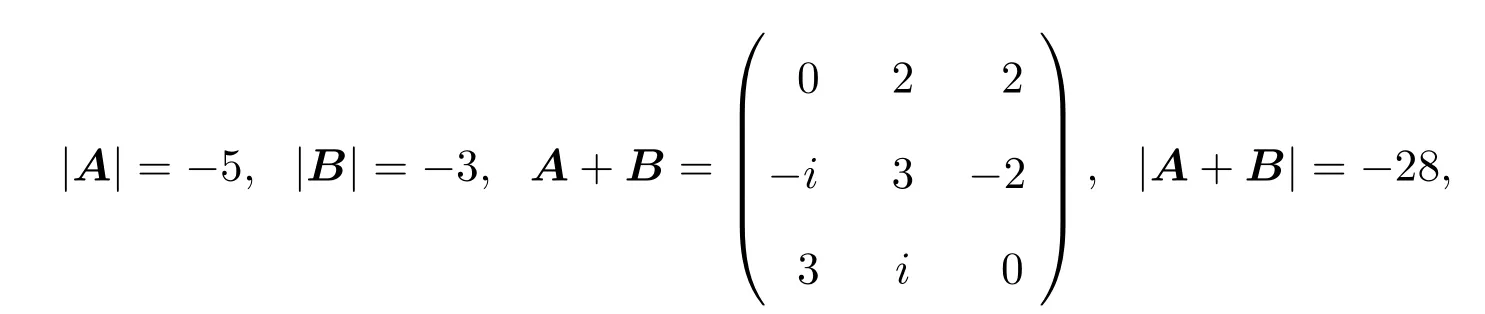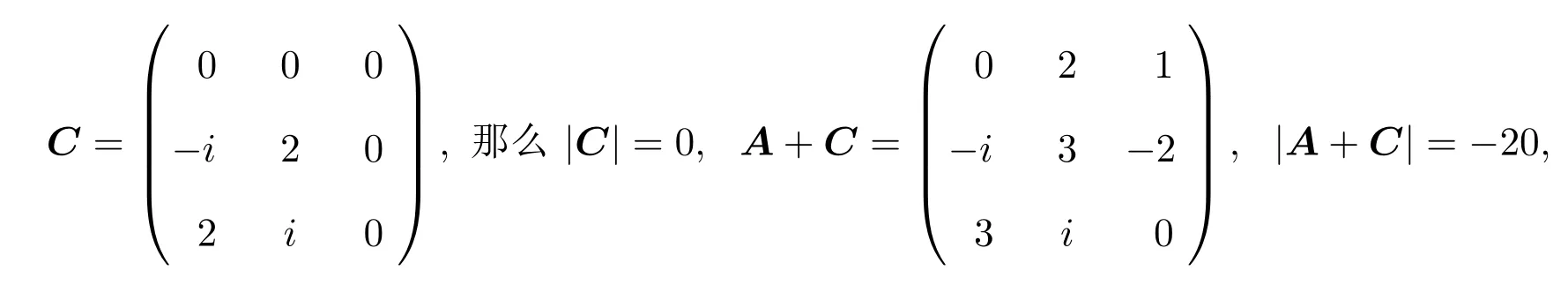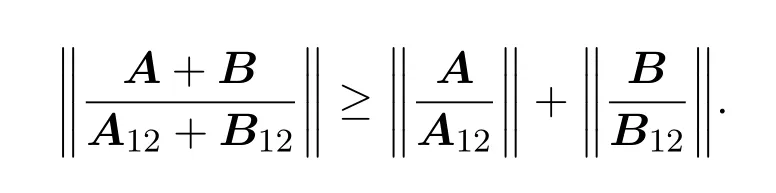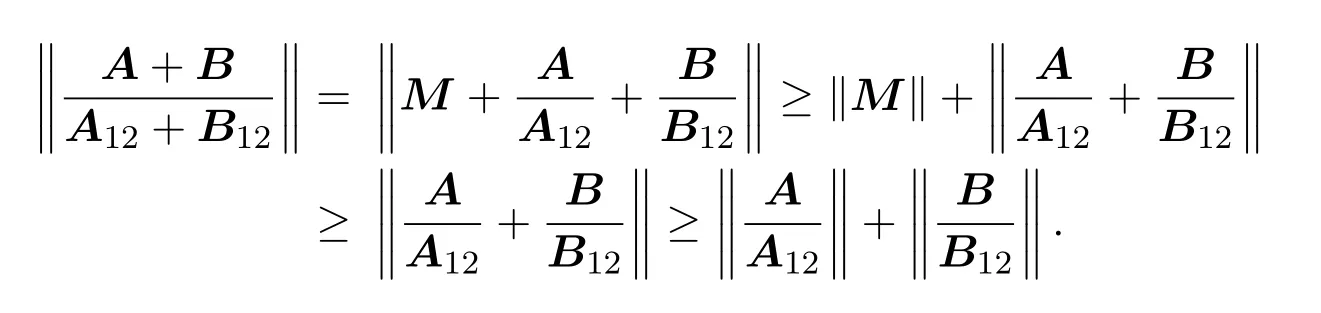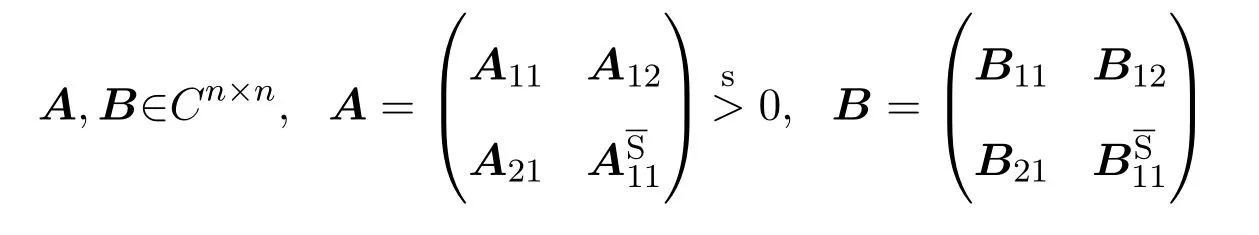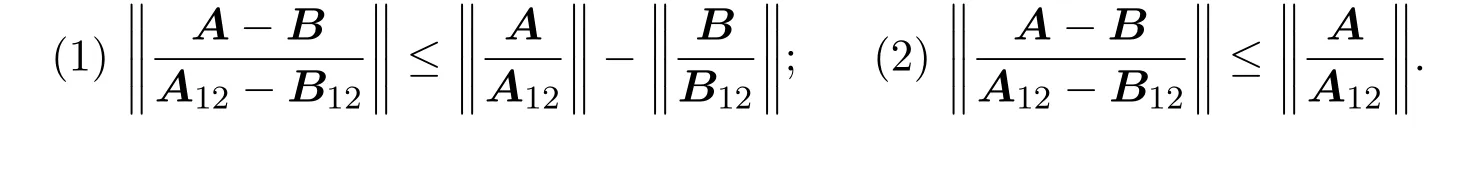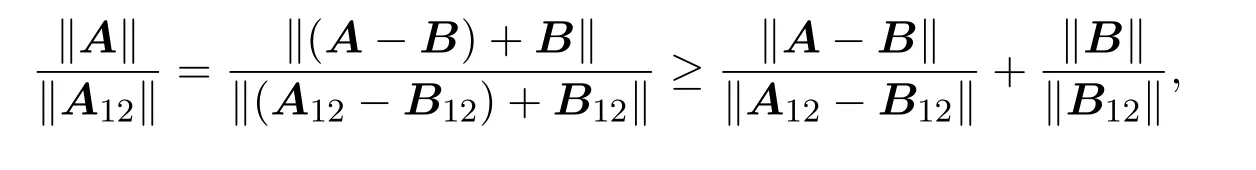次正定复矩阵次Schur补的一些性质
2014-07-18郑建青
郑建青
(宁波大学理学院,浙江宁波315211)
次正定复矩阵次Schur补的一些性质
郑建青
(宁波大学理学院,浙江宁波315211)
利用复矩阵的Schur补和次正定性,研究了次正定复矩阵的次Schur补的一些性质,得到了次正定复矩阵次Schur补的几个行列式不等式,将相关文献的相应结果由次正定次Hermite矩阵推广到次正定复矩阵.
次正定复矩阵;次Schur补;次正定次Hermite矩阵;共轭次转置矩阵
1 引言
复矩阵的次正定性是矩阵理论的重要组成部分,它的研究在矩阵理论或其应用中,有重要的意义和应用价值,并取得了诸多重要结果[1-4];矩阵Schur补在矩阵理论本身和统计学、数值计算等领域也有广泛应用,是近年来国内外矩阵研究的热点之一,同样取得了重要结果[5-9].笔者将两者结合起来,研究次正定复矩阵的次Schur补的一些性质,利用这些性质,探讨次正定复矩阵次Schur补的一些行列式不等式.
在本文中,用Cn×n表示n阶复矩阵集,表示A的共轭转置,表示A的共轭次转置,In表示n阶单位矩阵,Jn表示次对角线上的元素均为1而其它元素为0的n阶矩阵,|A|表示A的行列式,∥A∥表示A的行列式的模,记
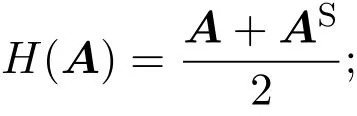
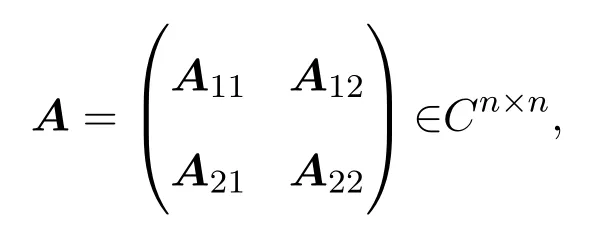
A12为k(1≤k 由文献[2-4],得到以下结论. 引理1设A,B∈Cn×n,有 (4)若存在可逆矩阵P∈Cn×n,使 定理1设 非奇异,则A关于A12的次Schur补: 证明因为由引理1得 由文献[8]定理2.1,JnA关于Jn−kA21的Schur补: 从而 定理2设 证明由假设,H(A12)可逆,令 则 定理3设 非奇异,则 证明由于 且 从而有 推论1设 非奇异,则 定理4设 证明 由恒等式[10]: 引理2则对于充分小的ε>0,有并且当ε→0时,有 证明由对充分小的ε>0,显然有.假设A的次特征值为其中存在n阶酉矩阵U,使 那么 当ε→0时, 定理5设A,BB为半次正定次Hermite矩阵,则当n>2时, 证明当B为次正定次Hermite矩阵,由JnA>0,JnB为正定次Hermite矩阵及文献[8]推论3.1得当n>2时, ∥JnA+JnB∥≥∥JnA∥+∥JnB∥,从而有∥A+B∥≥∥A∥+∥B∥; 例如若取次正定复矩阵: 次正定次Hermite矩阵: 那么 显然n=3,且∥A+C∥=20≥∥A∥+∥C∥=5,结论也成立. 推论2设A,B为半次正定次Hermite矩阵,则当n>2时, (1)∥A−B∥≤∥A∥−∥B∥; (2)∥A∥≥∥B∥. 证明(1)因由定理5,当n>2时, ∥A∥=∥(A−B)+B∥≥∥A−B∥+∥B∥, 故∥A−B∥≤∥A∥−∥B∥成立. (2)由(1),因∥A−B∥≥0,故∥A∥≥∥B∥. 定理6设 证明由定理1,由文献[5]定理1,B为次正定次Hermite矩阵,可得为次正定次Hermite矩阵,从而 由定理4, 为n−k阶半次正定次Hermite矩阵,由定理5,可得当n−k>2时,有 推论3设 证明(1)因 A=(A−B)+B,A12=(A12−B12)+B12, 从而有 (2)由(1)可知(2)成立. [1]曹莉莉.次Hermite矩阵的次正定性[J].西南师范大学学报:自然科学版,1996,21(3):235-238. [2]宋乾坤.复矩阵的次正定性[J].重庆师范大学学报:自然科学版,2001,18(1):51-54. [3]郭华.次正定矩阵的判别[J].湖北大学学报,2005,27(3):201-203. [4]郭华,李庆玉.次正定复矩阵[J].重庆工商大学学报:自然科学版,2006,23(4):347-350. [5]于江明,谢清明.次正定Hermite矩阵次Schur补的性质[J].数学杂志,2006,26(2):185-19. [6]Liu Jianzhou.Some inequalities for singular values and eignvalues of generalized Schur complements of products of matrices[J].L.A.A.,1999,293:233-241. [7]刘建州,谢清明.矩阵广义Schur补的复合矩阵的L¨owner偏序与奇异值[J].数学学报,2000,43(6):1071-1076. [8]袁晖坪.复正定矩阵的Schur补[J].高等数学研究,2000,3(2):33-36. [9]王桂松,吴密霞,贾忠贞.矩阵不等式[M].北京:科学出版社,2005. [10]屠伯埙.线性代数方法导引[M].上海:复旦大学出版社,1986. Some properties for sub-Schur complement of the subde fi nite complex matrix Zheng Jianqing (College of Science,Ninigbo University,Ningbo315211,China) Using the complex matrix property of Schur complement and subde fi niteness,Some complex matrix properties of sub-Schur complement are discussed,and its several determinant inequalities are obtained.The relative results of subde fi nite sub-Hermite matrix in reference have been extended to subde fi nite complex matrix. subde fi nite complex matrix,sub-Schur complement,subde fi nite sub-Hermite matrix, conjugate sub-transpose matrix O151.21 A 1008-5513(2014)01-0045-08 10.3969/j.issn.1008-5513.2014.01.008 2013-09-08. 宁波大学科研基金(理)(xkl1323,XYL13008). 郑建青(1975-),硕士,讲师,研究方向:矩阵理论. 2010 MSC:15A60
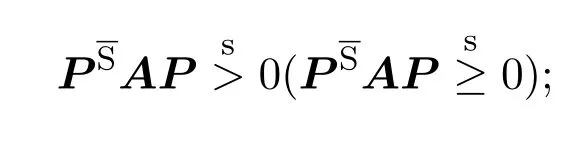

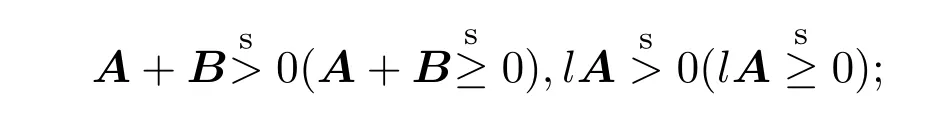
2 次Schur补的性质

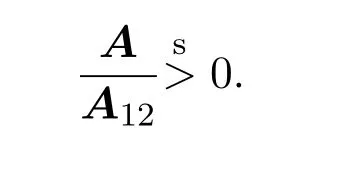





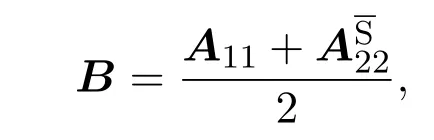
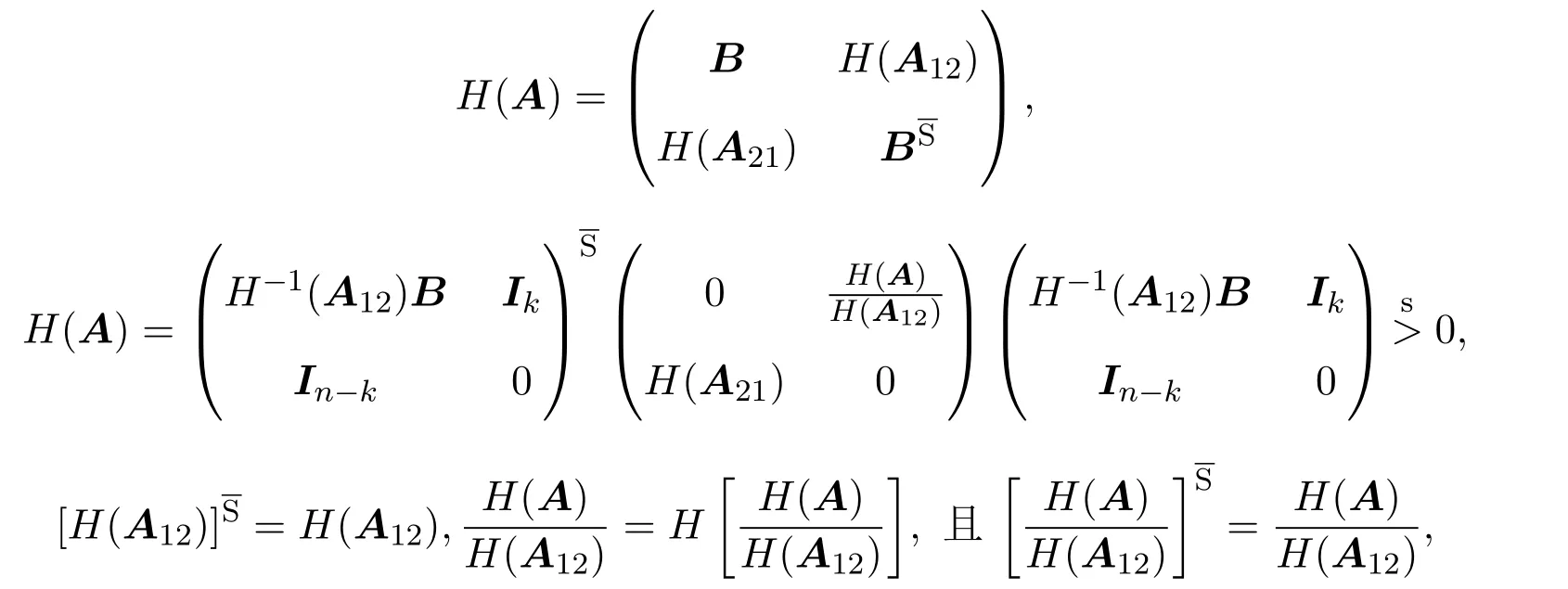


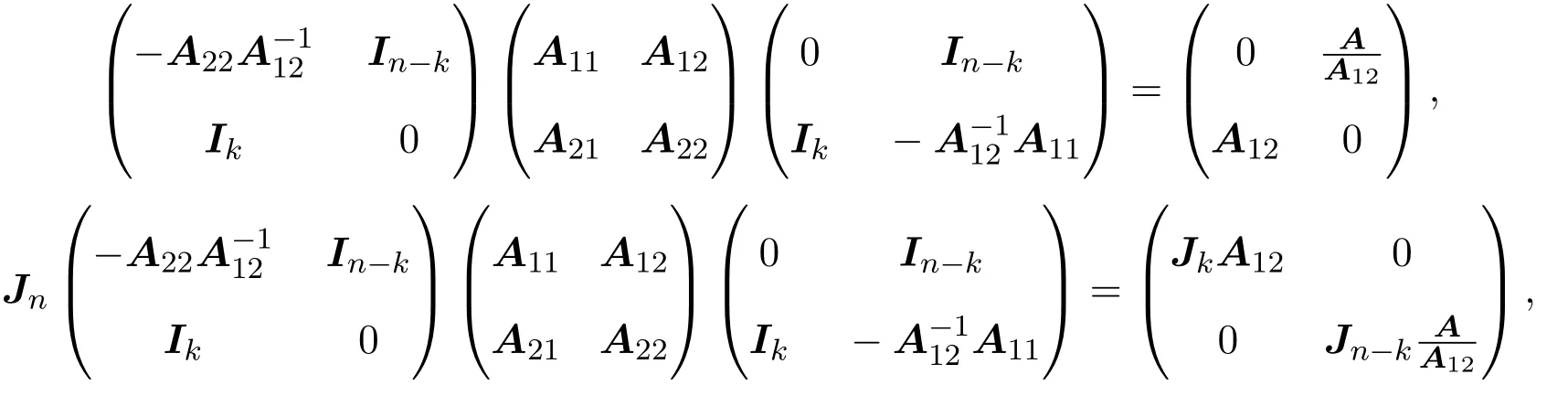

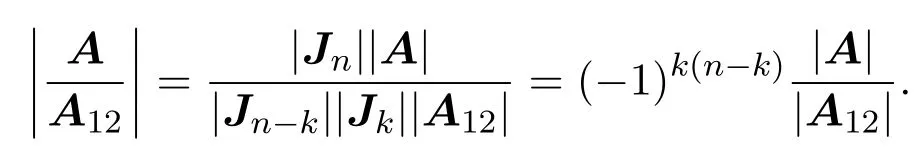
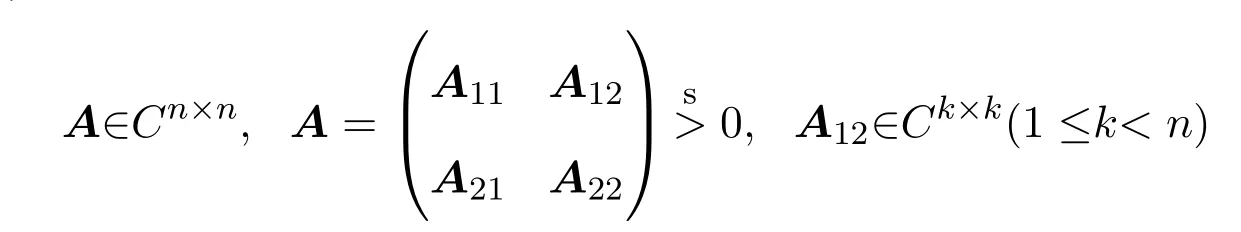

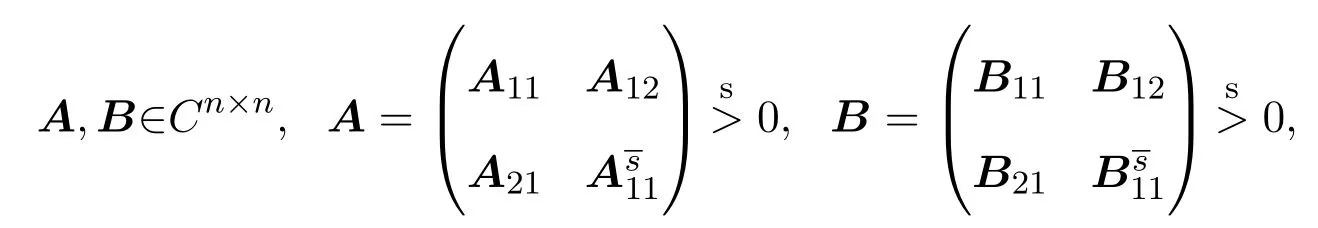




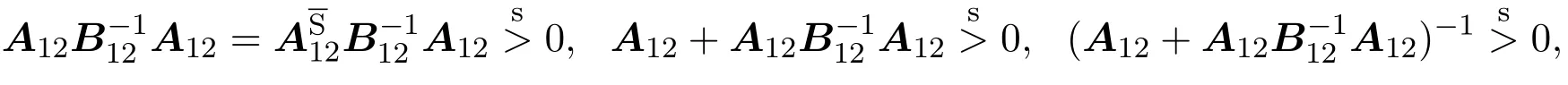
3 有关行列式不等式