单的模代数及其稳定化子

王彩虹,赵利辉

(1.河南理工大学数学与信息科学学院,河南焦作454000; 2.河南科技大学数学与统计学院,河南洛阳471023)

单的模代数及其稳定化子

王彩虹1,赵利辉2

(1.河南理工大学数学与信息科学学院,河南焦作454000; 2.河南科技大学数学与统计学院,河南洛阳471023)

研究了有限维Hopf代数H与其单的模代数A的smash积的结构.通过给出A的反代数与其极小左理想的稳定化子的结构,证明了H与A的smash积与某个代数上的全矩阵代数是代数同构的,推广了以往的结果.

Hopf代数;smash积;单的模代数;全矩阵代数

1 引言

稳定化子是研究代数结构的有效工具,许多文章都通过研究稳定化子得到了重要结果[13].本文将通过稳定化子研究Hopf代数与其模代数的smash积的结构.关于在哪些条件下smash积同构于某个代数上的全矩阵代数的问题,许多学者都有所研究,并得到了一系列的结果.

设k是一个域,G是有限群,X是可迁的有限G-集合,则群代数kG是一个有限维的Hopf代数,X上所有函数k(X)=Hom(X,k)构成一个交换代数.G在X上的作用在k(X)上诱导了一个kG-模代数结构.Harrison在文献[1]中证明了smash积k(X)#kG同构于kN上的全矩阵代数,其中N是某个x∈X的稳定化子.

如果H是域k上的n-维Hopf代数(n<∞),那么[5-6]:

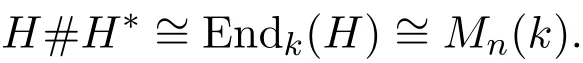
如果H是一个有限维Hopf代数,A是H∗的右余理想Frobenius子代数,则有代数同构K#H∗～=A⊗End(K)和A#H～=K⊗End(A),其中K=(H∗/A+H∗)∗⊆H(见文献[7]).

在特征为0的域上,如果H是一个半单的Hopf代数,A是一个可迁的H-模代数,并且有一个1-维理想kλ,那么smash积A#H代数同构于N上的全矩阵代数,其中

是H的右余理想子代数,并且N是可分代数[8].

容易看出,在以上结论中,Hopf代数H在模代数A上的作用都是可迁的,并且A都有一个1-维理想,这里可迁的概念是在文献[9]里定义的:

定义1.1设H是一个Hopf代数,A是H-模代数.H在A上的作用称为可迁的,如果此作用满足以下条件:

1.AH={a∈A|h·a=ε(h)a,∀h∈H}=k1A;

2.A只有平凡的H-理想.

本文主要研究当Hopf代数H及其单的模代数A都是有限维时,稳定化子和smash积A#H的结构.我们证明了在上述条件下smash积A#H代数同构于某个代数上的全矩阵代数.

2 预备知识

在本文中,k表示特征为0的代数闭域,所有的代数、Hopf代数、模等都是以k作为基域.如无特别指出,所有的模都指左模.

下面给出Hopf作用的稳定化子的概念[10].设H是一个有限维的Hopf代数,A是H-模代数,M是A-模,则有两个自然的嵌入映射

其中H(H)=H#H∗是文献[11]的4.1节中定义的Heisenberg double.设{hk}是H的k-基,是其对偶基,则有下面的H-模代数同态:

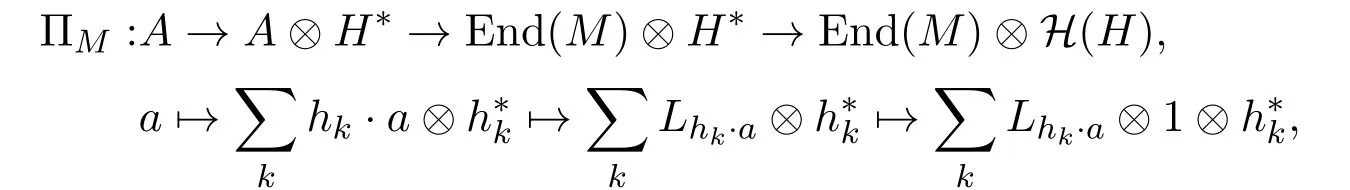
其中La(m)=a·m,∀a∈A,m∈M.定义

由文献[10],A′是一个右H∗-模代数.k-空间M有一个A′-模结构:

上面定义的A′-模记作M′,并将(A′,M′)称为(A,M)的稳定化子,在不引起混淆的情况下,本文也将A′称为A的稳定化子.

H-模代数A称为H-单的,如果A只有平凡的H-理想.因此,一个模代数是可迁的当且仅当它是H-单的,并且其不变量是平凡的.

2 主要结果

本节中,H表示一个有限维的Hopf代数,A表示有限维的单H-模代数,则A=Mn(k)是一个全矩阵代数,其基为矩阵单位{eij|1≤i,j≤n}.易见Aop是Hcop-模代数.将Aop中的乘法记为b◦a=ab.

引理3.1设I=k{el1,···,eln}是Aop的任一极小左理想,(A′,I′)是(Aop,I)的稳定化子,则A′=CA#H(A),其中CA#H(A)是A在A#H中的中心化子.

证明注意到End(I)有一组基定义映射

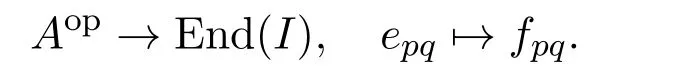
这个映射显然是代数同构,所以可将Aop和End(I)看作同一个代数,这样就有∑

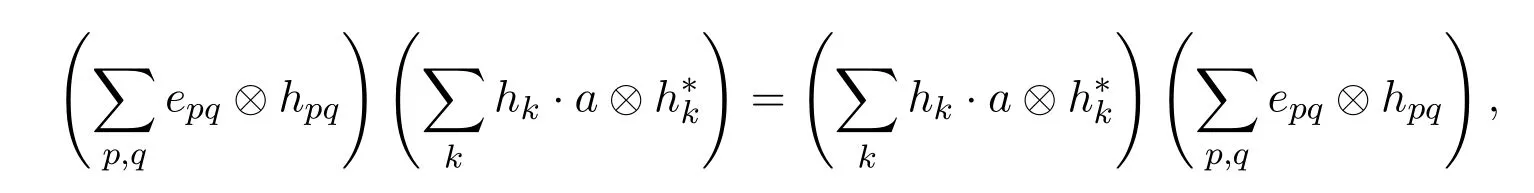
即

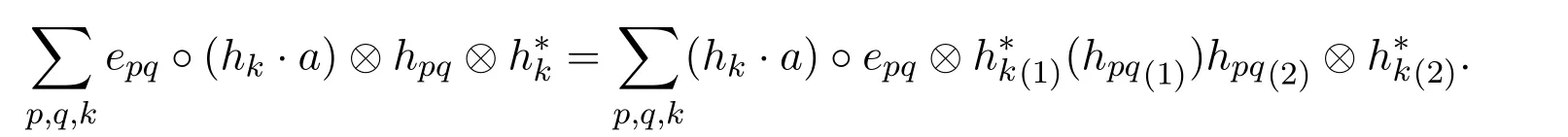
上式等价于对任意的g∈H,

即对任意的a∈A,

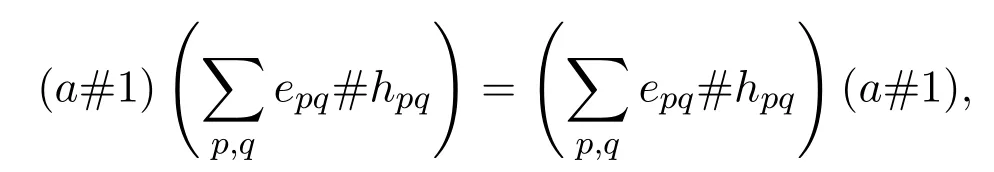
亦即

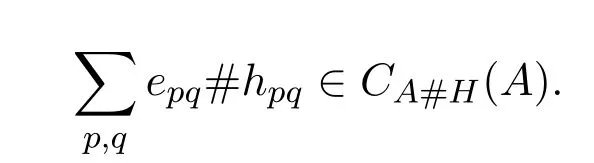
故A′=CA#H(A).

定理3.1如果dimA′=dimH,则smash积A#H～=Mn(k)⊗A′.

证明定义映射

由于对任意的x,x′∈A′和eij,ers∈Mn(k),

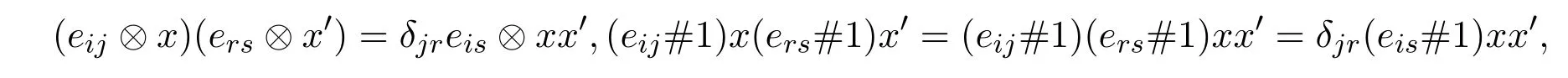
所以φ是代数同态.

下面证明φ是单射.如果

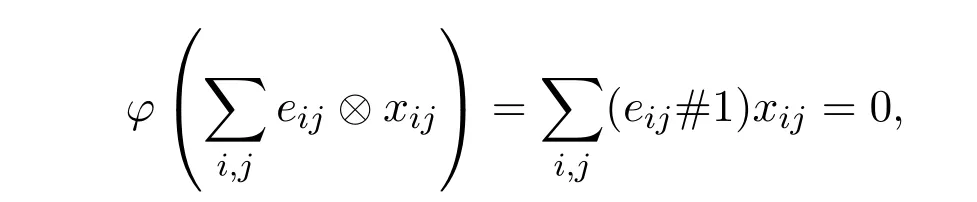
由引理3.1,对任意的1≤k,u,v≤n,

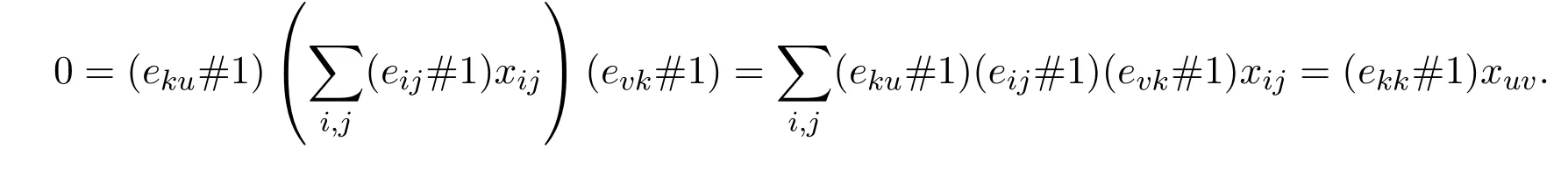
所以φ是代数同构.

例3.1设A=M2(k),Hopf代数H是群代数定义H在A上的作用为:

g·e11=e22,g·e22=e11,g·e21=e12,g·e12=e21.

定理3.2设I是Aop的任一左理想,(A′,I′)是(Aop,I)的稳定化子,则A#H～=而且,如果H是半单的,则有A′也半单.

证明由于A是单的H-模代数,Aop是单的Hcop-模代数.显然I是不可约的Aop-模,由文献[9]的推论2.8知:

dim(A)dim(A′)=(dim(I))2dim(H).

因此,dim(A′)=dim(H).再由定理3.1,所证的代数同构成立.如果H还是是半单的,则由文献[10]的定理5.2,A′也半单.

例3.2令G=〈x,y|x2=y3=1,xy=y−1x〉是非交换的6-阶群,Hopf代数H=kG.定义H在A=M2(k)上的作用为:

易证此作用下,A成为H-模代数.显然H是半单的,取H的积分则

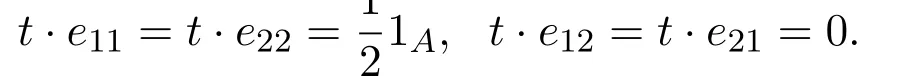
因此AH=k1A,从而A是可迁的H-模代数.取不可约的左Aop-模I=经计算可得:

[1]Mombelli M.Dynamical twists in Hopf algebras[J].Int.Math.Res.Not.,2007,(1):1-25.

[2]李旭东.N(2,2,0)代数的稳定化子与同余分解[J].纯粹数学与应用数学,2011,27(1):123-128.

[3]Skryabin S.Coring stabilizers for a Hopf algebra coaction[J].J.Algebra,2011,338:71-91.

[4]Harrison D K.K0of Hopf algebras and enlarged group algebras[J].Comm.Algebra,1984,12(2):149-198.

[5]Blattner R J,Montgomery S.A duality theorem for Hopf module algebras[J].J.Algebra,1985,95:153-172.

[6]Van Den Bergh M.A Duality Theorem for Hopf Algebras[M]//Vesselin Drensky,Antonio Giambruno, Sudarshan K.Sehgal.Methods in Ring Theory.New York:Marcel Dekker Inc,1984:517-522.

[7]Koppinen M.Coideal subalgebras in Hopf algebras:freeness,integrals,smash products[J].Comm.Algebra, 1993,21(2):427-444.

[8]Wang C,Zhu S.On smash products of transitive module algebras[J].Chin.Ann.Math.,2010,31B(4):541-554.

[9]Zhu Y.The dimension of irreducible modules for transitive module algebras[J].Comm.Algebra,2001,29(7): 2877-2886.

[10]Yan M,Zhu Y.Stabilizer for Hopf algebra actions[J].Comm.Algebra,1998,26(12):3885-3898.

[11]Montgomery S.Hopf Algebras and Their Actions on Rings[M].Providence,Rhode Island:American Mathematical Society,1993.

On simple module algebra and its stabilizer

Wang Caihong1,Zhao Lihui2

(1.School of Mathematics and Information Science,Henan Polytechnic University,Jiaozuo454000,China; 2.School of Mathematics and Statistics,Henan University of Science and Technology, Luoyang471023,China)

In this paper,the structure of the smash product of a fi nite-dimensional Hopf algebra H and its simple module algebra A is studied.By giving the structure of the stabilizer of the opposite algebra of A and its minimal left ideal,it is proved that,the smash product of H and A is algebraically isomorphic to a full matrix algebra over some algebra.The work generalizes the previous conclusions.

Hopf algebra,smash product,simple module algebra,full matrix algebra

O153.3

A

1008-5513(2014)01-0027-05

10.3969/j.issn.1008-5513.2014.01.005

2013-12-05.

国家自然科学基金(11101128,11301155);河南省教育厅自然科学基金(12B110008);河南省高等学校青年骨干教师资助计划项目(2012GGJS-061).

王彩虹(1979-),博士,讲师,研究方向：环与代数.

2010 MSC:16S40,16T05