超空间与原空间动力系统之间的关系

李金金

(西北大学数学系,陕西西安710127)

超空间与原空间动力系统之间的关系

李金金

(西北大学数学系,陕西西安710127)

设(X,d,f)为拓扑动力系统,其中X为局部紧可分的可度量化空间,d为紧型度量,f为完备映射,用2X表示由X的所有非空闭子集构成的集族,(2X,ρ,2f)为由(X,d,f)所诱导的赋予hit-or-miss拓扑的超空间动力系统.本文引入了余紧点传递和弱拓扑传递的定义.特别的,在X满足一定的条件时,给出了点传递,弱拓扑传递和余紧点传递之间的关系,并研究了(X,d,f)的余紧传递点,回复点和几乎周期点分别与(2X,ρ,2f)的传递点,回复点和几乎周期点之间的蕴含关系.这些结论丰富了赋予hit-or-miss拓扑的超空间的研究内容.

超空间动力系统;弱拓扑传递;余紧点传递;回复点;几乎周期点

1 引言

设X为一个拓扑空间,f:X→X是一个连续自映射,称(X,f)是一个拓扑动力系统, X是(X,f)的底空间.当(X,d)是度量空间时,把(X,f)记作(X,d,f).

记F和2X分别是拓扑空间X的所有闭子集和所有非空闭子集构成的集族.对任意一个子集A∈2X,定义2f(A)=f(A).假定给2X赋予某种拓扑,并且H是2X的一个子空间,如果f与H是相容的(即对H中任意的A,有f(A)∈H),且使得2f:H→H为连续映射,则称(H,2f)为由(X,f)所诱导的超空间动力系统.

设(X,d,f)是一个底空间为局部紧可分的可度量化空间的动力系统,且d为紧型度量,f为完备映射.2009年,文献[1]在F和2X分别赋予hit-or-miss拓扑时,给出了由(X,d,f)所诱导的超空间动力系统(F,ρ,2f)和(2X,ρ,2f).2007年,文献[2]对(X,d,f)和(2X,ρ,2f)上的混合性,弱混合性及传递性等一些动力性状进行了研究.2009年,文献[3]对(X,d,f)和(2X,ρ,2f)上的初值敏感性等一些动力性状进行了研究.2010年,文献[4]对(X,d,f)和(2X,ρ,2f)上的等度连续性等一些动力性状进行了研究.随后,2012年,文献[5]研究了赋予Vietoris拓扑的对称积拓扑动力系统与原空间拓扑动力系统之间关于周期性,回复性,影子性质等性状的蕴含关系. 2013年,文献[6]研究了超空间在赋予Vietoris拓扑,且底空间是紧致度量空间时的Martelli混沌.

本文在文献[5]的基础上研究了当(X,d,f)是一个底空间为局部紧可分的可度量化空间的动力系统,且d为紧型度量,f为完备映射,(2X,ρ,2f)为由(X,d,f)所诱导的赋予hit-ormiss拓扑的超空间动力系统时,引入了余紧点传递与弱拓扑传递的定义,进而通过一些例子给出了在X满足一定条件时余紧点传递与点传递,弱拓扑传递与拓扑传递的关系.最后得到了以下的结论:1)若A是所诱导的超空间动力系统中的拓扑传递点,则这个集合中的点是底空间的余紧传递点;2)单点集A是所诱导的超空间动力系统中的回复点当且仅当A中的点单是底空间的回复点;3)单点集A是所诱导的超空间动力系统中的几乎周期点当且仅当A中的点是底空间的几乎周期点.

2 基本定义及其概念

2.1 动力系统中的定义

定义2.1[7]设X是一个Hausdor ff拓扑空问,对X的任意非空开子集U,如果X−U是X的一个紧子集,则称U为一个余紧开集.

定义2.2[8]设X为局部紧可分的可度量化空间,ω(X)=X∪ω为X的一点紧化,和ωX上的度量,则称d为X上的紧型度量.

定义2.3[9]设X是一个Hausdor ff空间,f:X→Y,若f为连续的闭映射,且对于任意的y∈Y,f−1(y)为X的一个紧子集,则称f为一个完备映射.

定义2.4[10]设(X,f)是拓扑动力系统,对于正整数集合

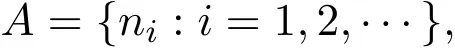
如果存在整数N>0,使得任意连续N个正整数中至少含有一个A中的元素,则称A是相对N稠密的.

定义2.5[10]设(X,d)为度量空间,x∈X,如果对于任意的ε>0,使得fn(x)∈V(x,ε)成立的n构成一个相对稠密的集合,则x称作f的几乎周期点.

定义2.6[10]设(X,d)为度量空间,x∈X,如果对于任意的ε>0,存在n>0,使得fn(x)∈V(x,ε),这里的

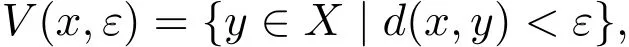
则x称作f的回复点.

定义2.7[10]设(X,f)是拓扑动力系统,如果存在x∈X,使得即x的轨道在X内稠密,则称f是点传递的,其中x称作f的传递点.

定义2.8设(X,f)是拓扑动力系统,x∈X,若对任意的余紧开集U⊆X,存在n≥0,使得fn(x)∈U,则称f是余紧点传递的,其中x称作f的余紧传递点.

从定义可以看出,点传递是余紧点传递的;当(X,d)为紧致度量空间,则余紧点传递与点传递是等价的.

而f的余紧传递点不一定是f的传递点,下面举一个例子来加以说明.

例1设X=Z+是离散的拓扑空间,即:X={1,2,3,···},其中f定义为:

f(x)=x+1,x∈X.

对于2∈X,由f的定义可知,X中任意一个非空余紧开集,2都会经过有限步之后落进这个非空余紧开集里,所以2是f的余紧传递点.而对于2∈X及开集{1},任意的n≥0,有fn(2)̸∈{1},则2不是f的传递点.

由例1可知,在非紧空间中,余紧传递点与传递点是不等价的.

下面给出f是余紧点传递,而f不是点传递的一个例子.

例2设X=Z+是离散的拓扑空间,即:X={1,2,3,···},其中f定义为:

f(x)=x2,x∈X.

对于2∈X及X的任意余紧开集U,都存在n≥0,使得fn(2)∈U,则2是f的余紧传递点,故f是余紧点传递的.而对于任意的x∈X及开集{2},对任意的n≥0,有fn(x)/∈{2},则f没有传递点,故f不是点传递的.

由例2可知,在非紧空间中,余紧点传递与点传递是不等价的.

定义2.9[11]设(X,f)是一个拓扑动力系统,若对任意的非空开集U,V⊆X,存在k≥0,使得fk(U)∩V̸=∅,则称f为拓扑传递的.

定义2.10设(X,f)是一个拓扑动力系统,若对任意的非空开集U,V⊆X,存在k≥0,

使得

fk(U)∩V̸=∅和fk(V)∩U̸=∅

至少有一个成立,则称f为弱拓扑传递的.

从定义不难看出,拓扑传递一定是弱拓扑传递的.而弱拓扑传递不一定是拓扑传递的,下面举一个例子来加以说明.

例3设

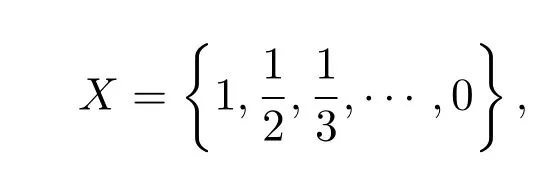
其中f定义为:

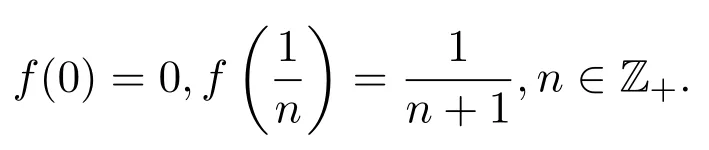
由于对任意的两个非空开集U和V,根据映射f的定义可知,0只是一个不动点,则在开集U和V中肯定有最小的元素,不妨设

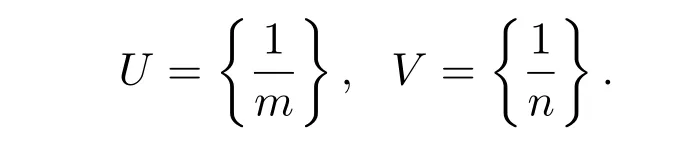
1)当m=n时,只需取k=0,有

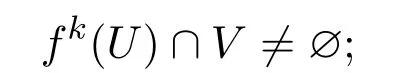
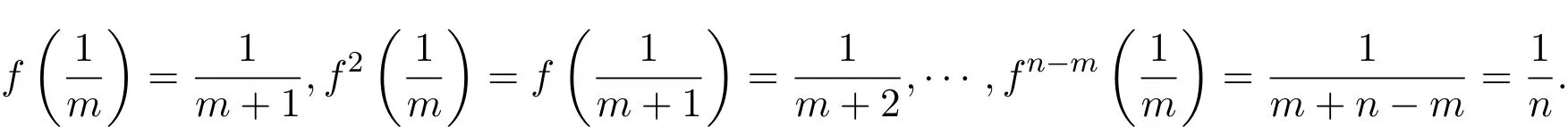
从而

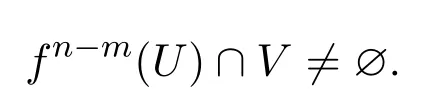
故由1)和2)知,f为弱拓扑传递的.

而对于开集

任意的k≥0,fk(V)∩U=∅,则f不是拓扑传递的.

由例3可知,弱拓扑传递与拓扑传递是不等价的.

下面给出点传递,余紧点传递与弱拓扑传递的关系,首先给出下面的一个引理.

引理2.11[11]设X为无孤立点的度量空间,f是X上的一个连续自映射,则

(a)若x∈X在映射f下有稠密的轨道,则对于任意的n≥1,fn(x)也有稠密的轨道;

(b)若映射f有稠密的轨道,则f也是拓扑传递的.

从引理2.11和定义2.10可以看出,当X为无孤立点的度量空间时,则点传递一定是弱拓扑传递的.

下面给出文献[12]的一个拓扑传递而非点传递的例子.

例4设g:I→I,其中I=[0,1],g(x)=1−|2x−1|为帐篷映射,则令X

由例4可知,当X为无孤立点的非紧致空间时,则f是拓扑传递而不是点传递的,从而f也是弱拓扑传递的而不是点传递的.

于是结合以上所得到的结果可得以下的关系:

(1)当X为非紧致的度量空间,且X无孤立点时,有

f是弱拓扑传递的⇐=f是拓扑传递⇐=f是点传递=⇒f是余紧点传递;

(2)当X为紧致的度量空间,且X无孤立点时,有

f是余紧点传递⇐⇒f是点传递⇐⇒f是拓扑传递=⇒f是弱拓扑传递.

2.2赋予hit-or-miss拓扑的超空间动力系统

设X为一个拓扑空间,按照Matheron G的记法[13],对于任意的B⊆X,A⊆P(X),其中P(X)为X的幂集,

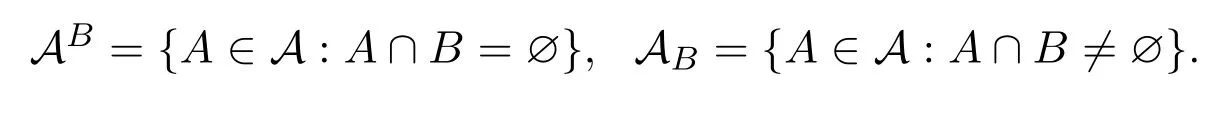
记F,G和K分别表示X中的所有闭集,开集和紧子集构成的集族(其中,空集但由集族

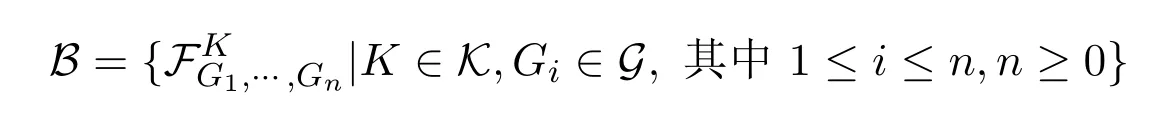
作为基底在F上所生成的拓扑τf称为hit-or-miss拓扑,其中

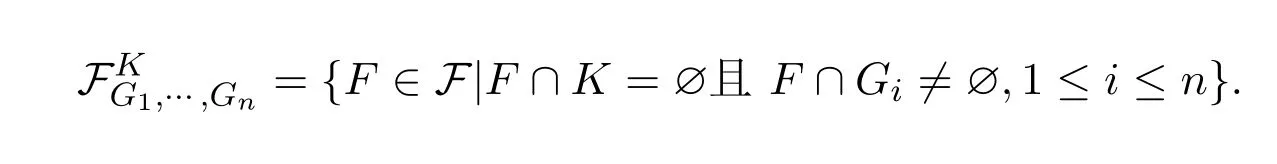
由集族

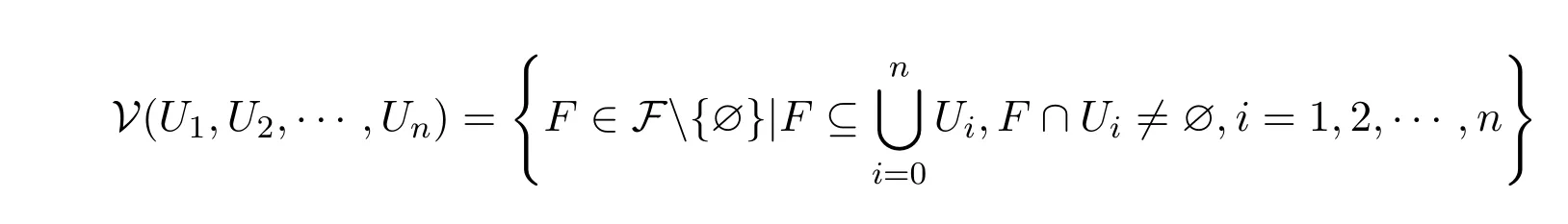
特别的,当X为局部紧第二可数的Hausdor ff拓扑空间时,F为紧致的第二可数的Hausdor ff拓扑空间,并且(F,τf)是可度量化的[14],2X作为F的子空间为局部紧第二可数的Hausdor ff拓扑空间,根据文献[15],(F,τf)上的一个相容度量为ρ:F×F→R,具体构造如下:

dH为:对任意的A,B∈2ωX,

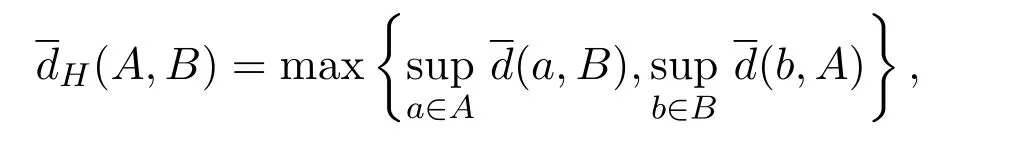
其中

定义映射C:F→2ωX为:对于任意的F∈F,C(F)=F∪{ω}.

度量ρ定义为:对任意的F,

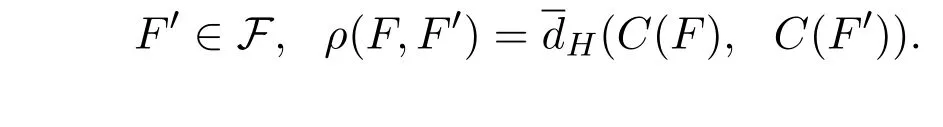
对于拓扑动力系统(X,d,f),其中(X,d)是局部紧第二可数的度量空间,d为紧型度量, f为完备映射.

由f所诱导的超空间上的映射2f:2X→2X定义为:对任意的F∈2X,2f(F)=f(F).由文献[15]知,2f为连续映射,从而(2X,ρ,2f)为一个拓扑动力系统.

3 主要结果

从本节开始,当提到(X,d,f)是一个拓扑动力系统时,就是指(X,d)为局部紧可分的可度量化空间,d为紧型度量,f:X→X为完备映射,其中(2X,ρ,2f)为由(X,d,f)所诱导的赋予hit-or-miss拓扑的超空间动力系统.

本部分是受文献[5]的启发,由于文献[5]研究了赋予Vietoris拓扑的对称积拓扑动力系统与原空间动力系统之间关于周期性,回复性,影子性质等性状的蕴含关系,于是在超空间赋予hit-or-miss拓扑时,对拓扑动力系统(X,d,f)与它所诱导的超空间拓扑动力系统(2X,ρ,2f)之间关于一些性状的蕴含关系进行了研究,提出了在适当增减条件的前提下可以得出本节的结果.

定理3.1设(X,d,f)是拓扑动力系统,f:X→X为完备映射,若A是(2X,ρ,2f)的传递点,则对任意的x∈A,x是(X,d,f)的余紧传递点.

证明设U是X的任意非空余紧开集,由于A是(2X,ρ,2f)的传递点,则对于非空开集存在使得

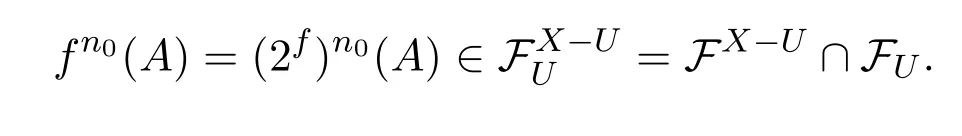
而

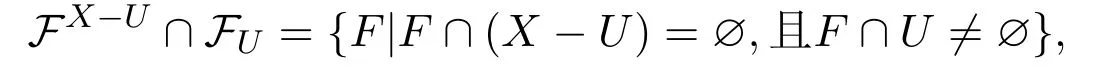
则有

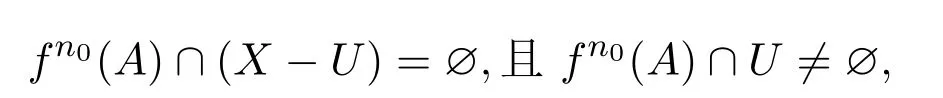
于是fn0(A)⊆U,从而对任意的x∈A,有fn0(x)∈fn0(A)⊆U,即对任意的x∈A, fn0(x)∈U.

故对任意的x∈A,x是(X,d,f)的余紧传递点.

由于在(X,d)为紧致度量空间时,Vietoris拓扑与hit-or-miss拓扑是一致的,结合定理3.1与第二部分的结果可得到下述推论.

推论3.2[6]设(X,d)为紧致度量空间,f:X→X为一个连续映射,其中(2X,ρ,2f)是由动力系统(X,d,f)所诱导的赋予Vietoris拓扑的超空间动力系统.若A是(2X,ρ,2f)的传递点,则对任意的x∈A,x是(X,d,f)的传递点.

从定理3.1可以看出,超空间中的拓扑传递点A,得到A中任意的点是底空间的余紧传递点.

定理3.3设(X,d,f)为拓扑动力系统,f:X→X为完备映射,则单点集A是(2X,ρ,2f)的回复点当且仅当单点集A中的点是(X,d,f)的回复点.

证明必要性由于A是(2X,ρ,2f)的回复点,且A是单点集,不妨令A={x},则对于任意的使得

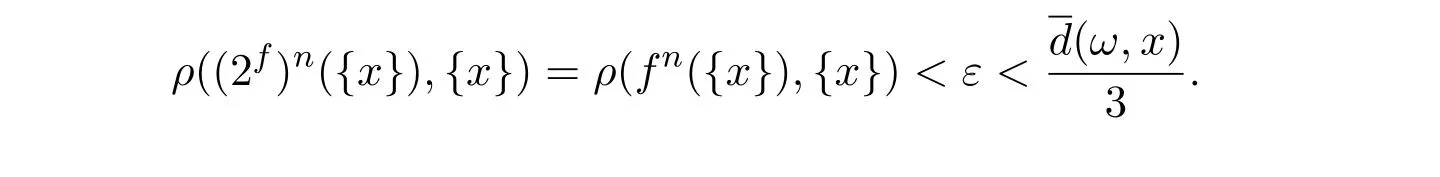
又由于

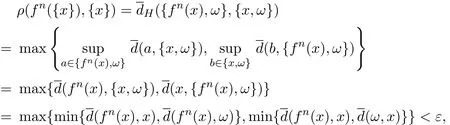
则有

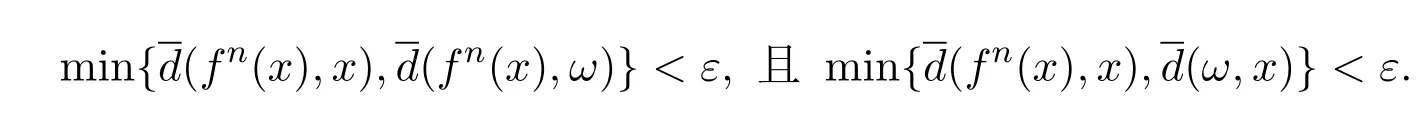
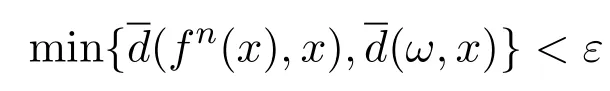
从而d(fn(x),x)<ε.

故A中的点是(X,d,f)的回复点.

充分性由于A是单点集,不妨令A={x}.因为x∈X是(X,d,f)的回复点,所以对于任意的存在n>0,使得

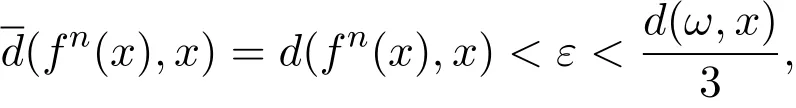
从而由三角不等式得

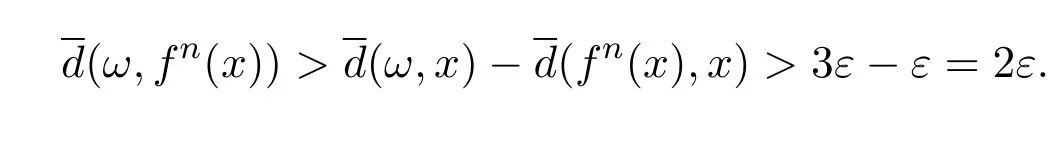
又由于

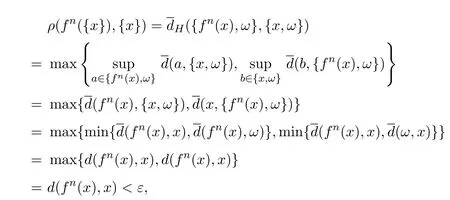
故单点集A是(2X,ρ,2f)的回复点.

定理3.4设(X,d,f)为拓扑动力系统,f:X→X为完备映射,则单点集A是(2X,ρ,2f)的几乎周期点当且仅当单点集A中的点是(X,d,f)的几乎周期点.

证明必要性由于A是(2X,ρ,2f)的几乎周期点,且A是单点集,不妨令A={x},则对于任意的存在n>0,使得成立的n构成相对稠密的集合N.

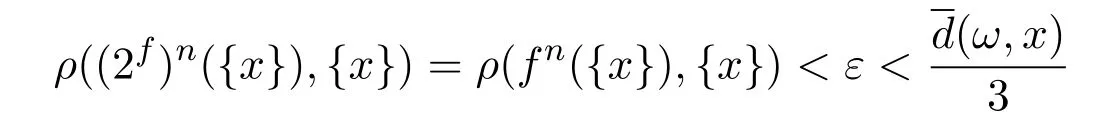
运用定理3.3必要性的证明方法,可得d(fn(x),x)<ε.

又因为N是相对稠密集,且N中的每一个n也使得d(fn(x),x)<ε成立,所以满足d(fn(x),x)<ε成立的n构成的集合也是相对稠密的.

故A中的点是(X,d,f)的几乎周期点.

充分性由于A是单点集,不妨令A={x}.因为x∈X是(X,d,f)的几乎周期点,所以对于任意的存在n>0,使得

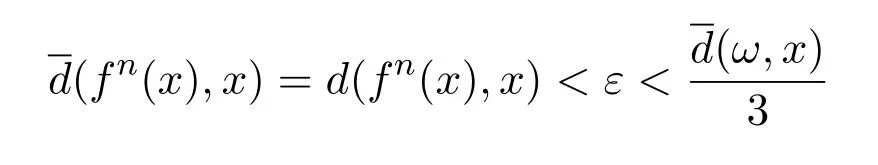
成立的n构成相对稠密的集合N,从而由三角不等式得

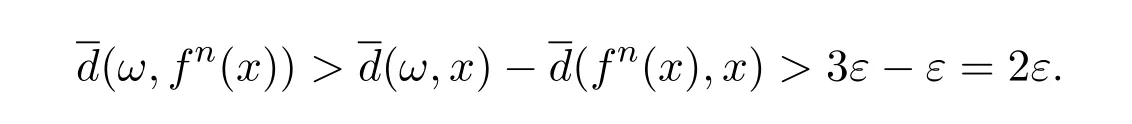
运用定理3.3充分性的证明方法,可得

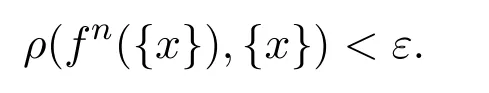
又因为N是相对稠密集,且N中的每一个n也使得ρ(fn({x}),{x})<ε成立,所以满足ρ(fn({x}),{x})<ε成立的n构成的集合也是相对稠密的.

故单点集A是(2X,ρ,2f)的几乎周期点.

从定理3.3与定理3.4可以看出,当超空间中的点是底空间的单点集时,超空间中的点所具有的动力性状与此点回到底空间所具有的一些动力性状是一样的.

[1]Wang Y G,Wei G,Campbell W H,et al.A framework of induced hyperspace dynamical systems equipped with the hit-or-miss topology[J].Chaos,Solitons,&Fractals,2009,41:1708-1717.

[2]Wang Y G,Wei G.Characterizing mixing,weak mixing and transitivity of induced hyperspace dynamical systems[J].Topology and its Applications,2007,155:56-68.

[3]Wang Y G,Wei G,Campbell W H.Sensitive dependence on initial condition between dynamical systems and their induced hyperspace dynamical systems[J].Topology and its Applications,2009,156:803-811.

[4]苗小倩.关于拓扑动力系统及其诱导的超空间动力系统的等度连续[J].西北大学学报:自然科学网络版,2010, 8(4):0436-0443.

[5]Jos´e L G´omez-Rueda,Alejandro Illanes,H´ector M´endez.Dynamic properties for the induced maps in the symmetric products[J].Chaos,Solitons,&Fractals,2012,45:1180-1187.

[6]Liu Lei,Zhao Shuli.Martelli’s chaos in inverse limit dynamical systems and hyperspace dynamical systems[J].Results Math.,2013,63:195-207.

[7]魏征,王延庚,卫国.一种新的拓扑熵[J].西北大学学报:自然科学网络版,2009,7(1):100-108.

[8]Wang Y G,Wei G,Li R.hit-or-miss拓扑上的度量:直接扩充[J].纯粹数学与应用数学,2008,24(4):643-645.

[9]Engelking R.General Topology[M].Warszawa:PWN,1977.

[10]周作领.符号动力系统[M].上海:上海科技教育出版社,1997.

[11]Karl-G Grosse-Erdmann,Alfred Peris Manguillot.Linear Chaos[M].London:Springer London Ltd.,2011.

[12]张景中,熊金城.函数迭代与一维动力系统[M].成都:四川教育出版社,1992.

[13]Matheron G.Random Sets and Integral Geometry[M].New York:Wiley,1975.

[14]Flachsmeyer J.Verschiedene topologisierungen im Raum der abgeschlossenen Teilmengen[J].Math.Nachr., 1964,26:321-337.

[15]Wei G,Wang Y G.On metrization of hit-or-miss topology Alexandro ffcompacti fi cation[J].International Journal of Approximate Reasoning,2007,46(1):47-64.

The relationships between hyperspace dynamical systems and original space

Li Jinjin

(Department of Mathematics,Northwest University,Xi′an710127,China)

Let(X,d,f)be a topological dynamical system,where X is a locally compact separable metrizable space,d is a compact-type metric and f is a perfect mapping.Let 2Xbe the space of all non-empty closed subsets of X.Let(2X,ρ,2f)denote the hyperspace dynamical systems induced by(X,d,f)equipped with the hit-or-miss topology.In this paper,the concepts of co-compact point transitivity and weak topological transitivity are introduced.In particular,when X satis fi es certain condition,the relationships between point transitivity,weak topological transitivity and co-compact point transitivity are given,and the author studied the relationships between co-compact transitivity point,recurrent point and almost period point of(X,d,f) respectively and transitivity point,recurrent point and almost period point of(2X,ρ,2f).These conclusions enriched the contents of induced hyperspace dynamical systems equipped with the hit-or-miss topology.

hyperspace dynamical system,weak topological transitivity,co-compact point transitivity, recurrent point,almost period point

O189.11

A

1008-5513(2014)01-0060-09

10.3969/j.issn.1008-5513.2014.01.010

2014-01-14.

国家自然科学基金(11301417);国家青年基金(11371292).

李金金(1986-),硕士生,研究方向：拓扑动力系统.

2010 MSC:54A05