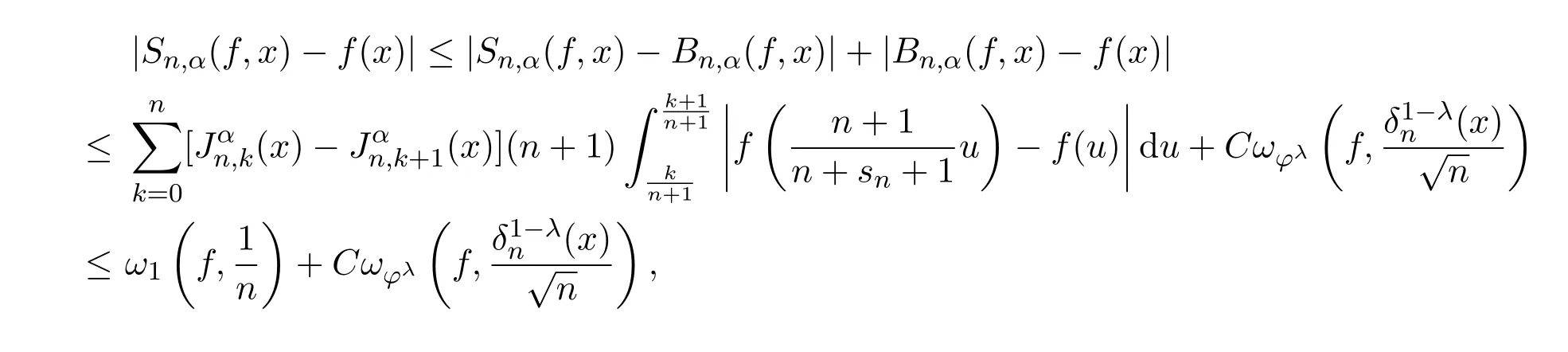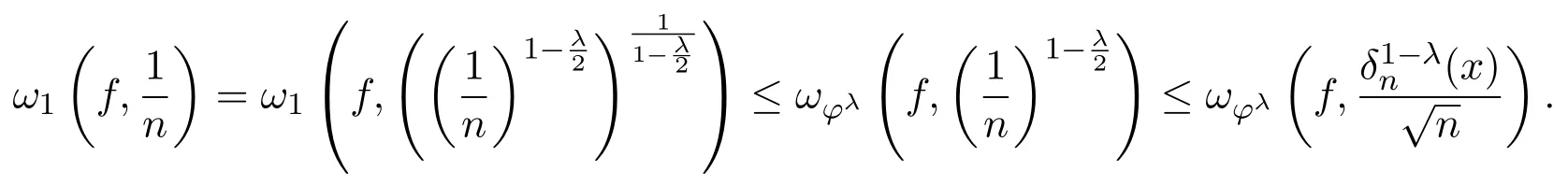一类推广的Bernstein-Kantorovich算子的点态逼近
2014-07-18刘国芬
刘国芬
(1.河北师范大学数学与信息科学学院,河北石家庄050024; 2.河北省计算数学与应用重点实验室,河北石家庄050024)
一类推广的Bernstein-Kantorovich算子的点态逼近
刘国芬1,2
(1.河北师范大学数学与信息科学学院,河北石家庄050024; 2.河北省计算数学与应用重点实验室,河北石家庄050024)
讨论Bernstein-Kantorovich算子的一种推广形式的逼近性质,运用插项的方法证明了逼近正定理,并证明了逆定理,得到了逼近等价定理.完善了算子在逼近性质方面的结果.
Bernstein-Kantorovich型算子;光滑模;K-泛函;逼近正逆定理
1 引言
对于f∈C[0,1],Bn(f,x)表示Bernstein-Kantorovich算子,定义[1]
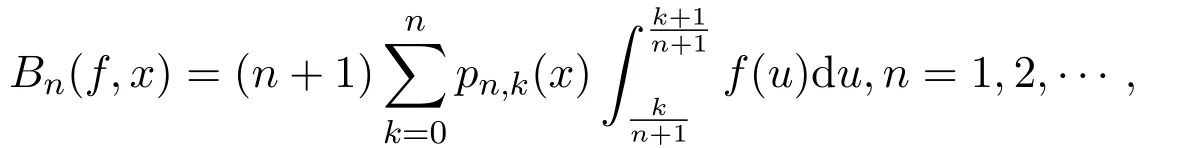
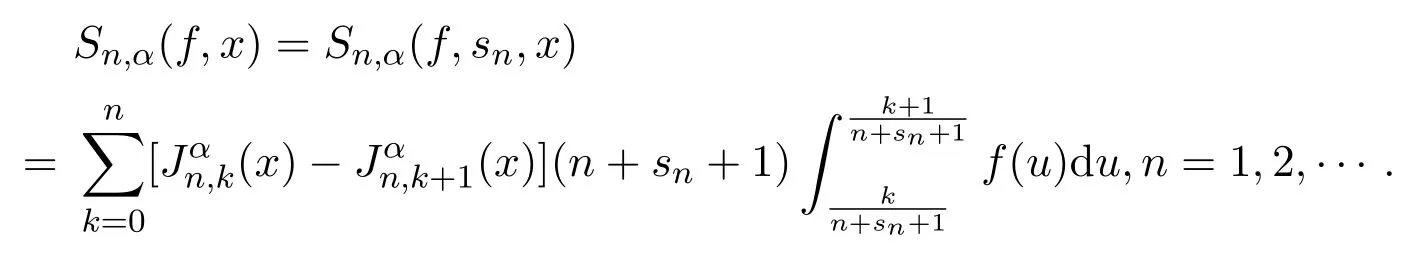
这里,
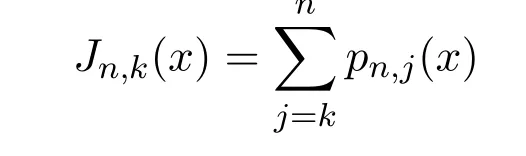
是B´ezier基算子,sn是一个自然数序列并且对于Sikkema算子[3]和B´ezier算子[4-7]许多学者都有一定的研究,对Bernstein-Sikkema-B´ezier算子的点态逼近性质进行了讨论[8],证明了其逼近的等价定理.本文将对Bernstein-Kantorovich的Sikkema-B´ezier变形算子的逼近性进行讨论,给出并证明该算子逼近的正逆定理和等价定理,其中主要结论叙述如下.
定理1设则下面两个陈述是等价的:
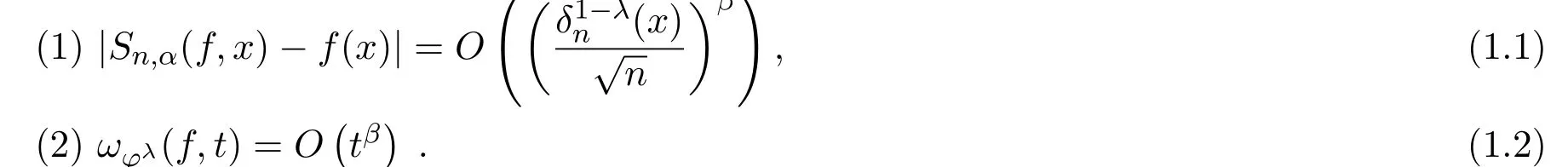
文中用到光滑模和K-泛函的等价性,它们的定义分别为:
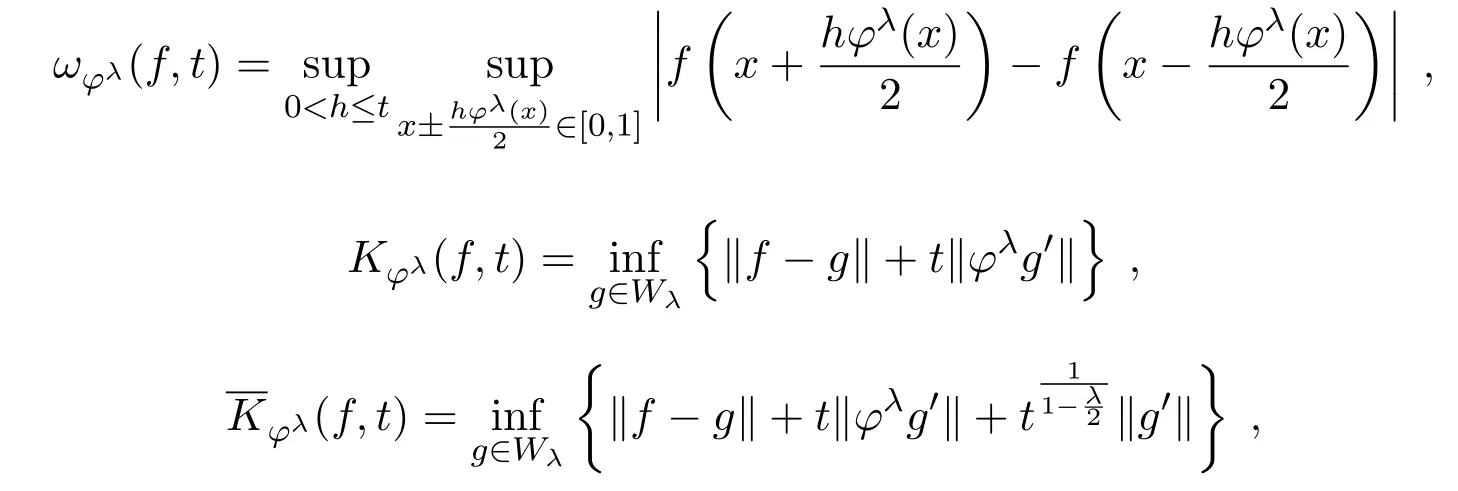
这里
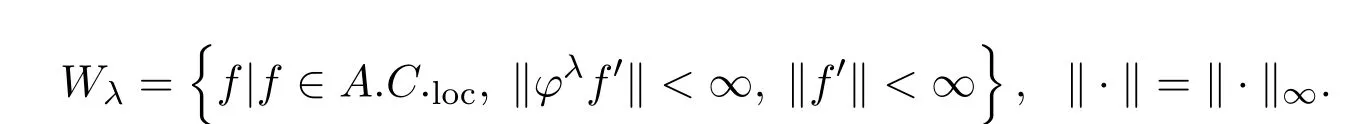
文中C表示与n和x都无关的常数,不同位置的数值可能是不一样的.
2 引理
为了证明定理1,需要几个引理.为了利用插项的方法,首先给出Bernstein-Kantorovich-B´ezier算子的逼近度,定义为
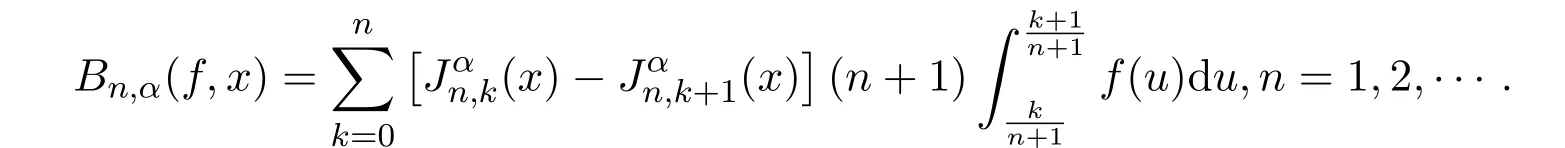
引理2.1设
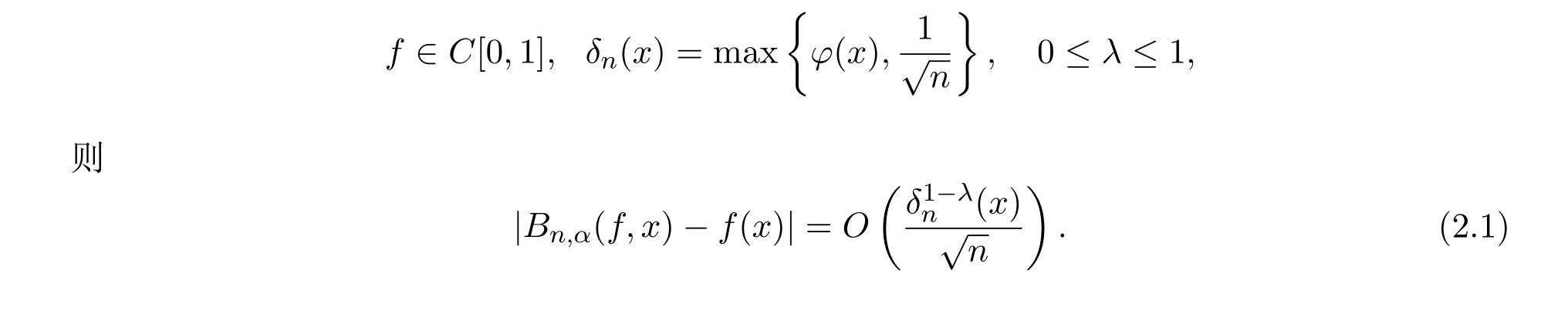
证明由与光滑模之间的等价关系,对于固定的n,x和λ,可以选择适当的g=gn,x,λ,使得
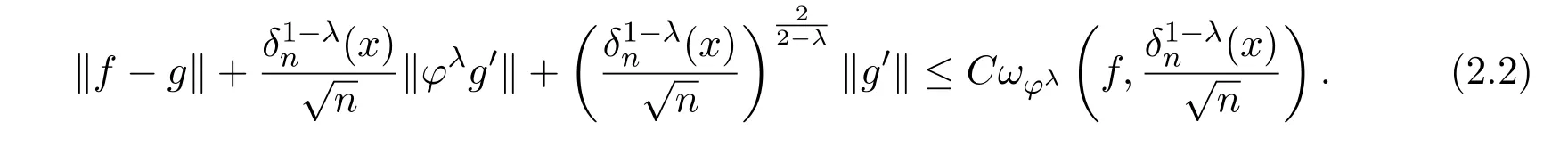
注意到|Bn,α(f)|≤α∥f∥,
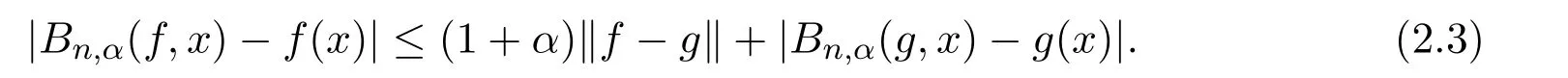
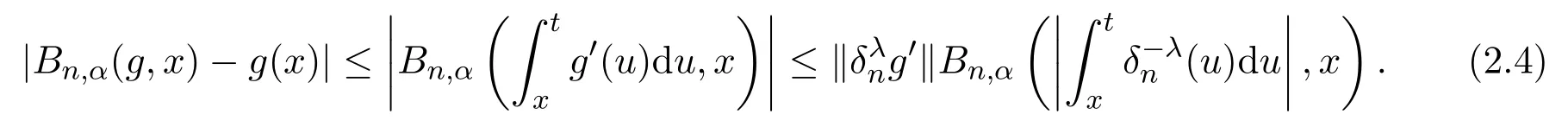
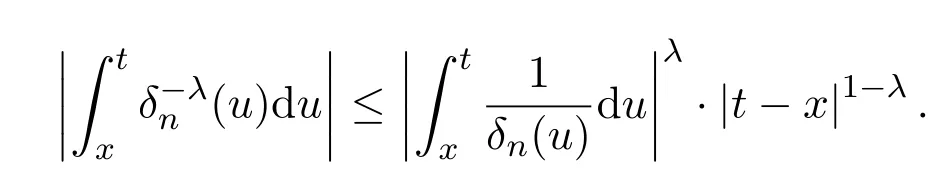
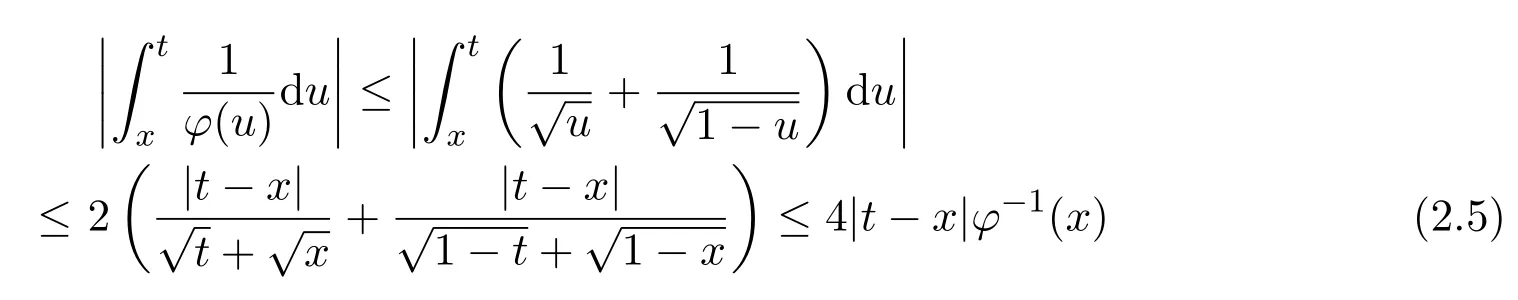

注意到0 可推出[1]: 利用(2.2)-(2.4)和(2.7)式,引理2.1得证. 引理2.2下面关于Sn,1(f,x)的矩的估计: 证明经过简单的计算就可得到Sn,1(1,x)=1, 成立.于是(2.8)式得证. 引理2.3设 则有 进一步,当f∈Wλ时, 证明首先证明(2.9)式. 这里 利用1=Jn,0>Jn,1>···>Jn,n>0和 注意到pn,n+1(x)=0,pn,−1(x)=0,结合,有 当x∈En时,δn(x)~φ(x), 结合(2.11)和(2.12)式,证明了(2.9)式.下面证明(2.10)式. 由于Sn,α(1,x)=1,显然f(x)S′n,α(1,x)=0.当f∈Wλ时,有 于是由(2.6)式,可得 注意到pn,−1(x)=0,当时, 这里 对于K1,有(当x=0时,K1=0), 另一方面, 对于x∈En,δn(x)~φ(x), 显然对于x∈En(2.14)式的推导过程也是适用的,I1≤C.于是当x∈En时,有 由(2.15)和(2.16),(2.10)式成立.这样引理2.3得证. 引理2.4当0时,不等式 证明对于(2.17),利用H¨older不等式只需证明: 这一部分将对定理1进行证明.对于(1.2)⇒(1.1)式,由引理2.1, 再由文献[1]中的(3.1.5)得到, 于是(1.1)式成立.另一方面,利用引理2.3和引理2.4并借助文献[9]中定理1关于“⇒”的方法就可以证明(1.1)⇒(1.2)式,这里不再叙述细节. [1]Ditzian Z,Totik V.Moduli of Smoothness[M].New York:Springer-Verlag,1987. [2]程丽.Bernstein-Kantorovich算子线性组合同时逼近的正逆定理[J].纯粹数学与应用数学,2011,27(1):56-62. [3]Cao J D.A Generalization of the Bernstein polynomials[J].J.Math.Anal.and Appl.,1997,209:140-146. [4]Chang G Z.Generalized Bernstein-B´ezier polynomial[J].J.Comput.Math.,1983,1(4):322-327. [5]Liu Z X.Approximation of continuous by the generalized Bernstein-B´ezier polynomials[J].Approx.Theory Appl.,1986,4(2):105-130. [6]Zeng X M,Piriou A.On the rate of convergence of two Bernstein-B´ezier type operators for bounded variation functions[J].J.Approx.Theory,1998,95:369-387. [7]Guo S S,Qi Q L,Liu G F.The central approximation theorem for Baskakov-B´ezier operators[J].J.Approx Theory,2007,147:112-124. [8]刘国芬.Bernstein-Sikkema-B´ezier算子的点态逼近[J].数学的实践与认识,2013,43(1):199-204. [9]Guo S S,Liu L X,Qi Q L.Pointwise estimate for linear combinations of Bernstein-Kantorovich operators[J]. J.Math.Anal.Appl.,2002,265:135-147. Pointwise approximation for a generalization of Bernstein-Kantorovich operators Liu Guofen1,2 (1.College of Mathematics and Information Science,Hebei Normal University,Shijiazhuang050024,China; 2.Hebei Key Laboratory of Computational Mathematics and Applications,Shijiazhuang050024,China) We study the properties of approximation for a generalization of Bernstein-Kantorovich operators and prove the direct approximation theorem by the means of inserting term and the inverse theorem,namely the equivalence theorem.The results of the properties of approximation for this kind of operators are perfected. generalized Bernstein-Kantorovich operators,modulus of smoothness,K-functional, direct and inverse approximation theorem O174.41 A 1008-5513(2014)01-0032-08 10.3969/j.issn.1008-5513.2014.01.006 2008-02-10. 国家自然科学基金(10801043). 刘国芬(1974-),博士,讲师,研究方向:函数逼近论. 2010 MSC:41A25,41A26,41A36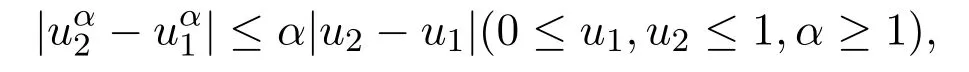
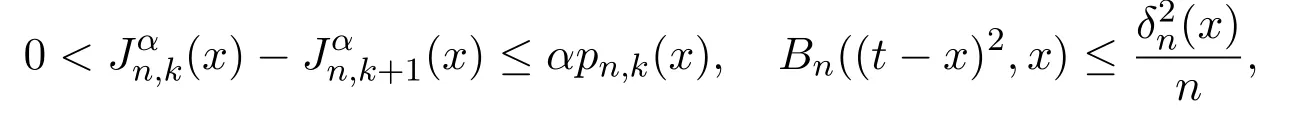
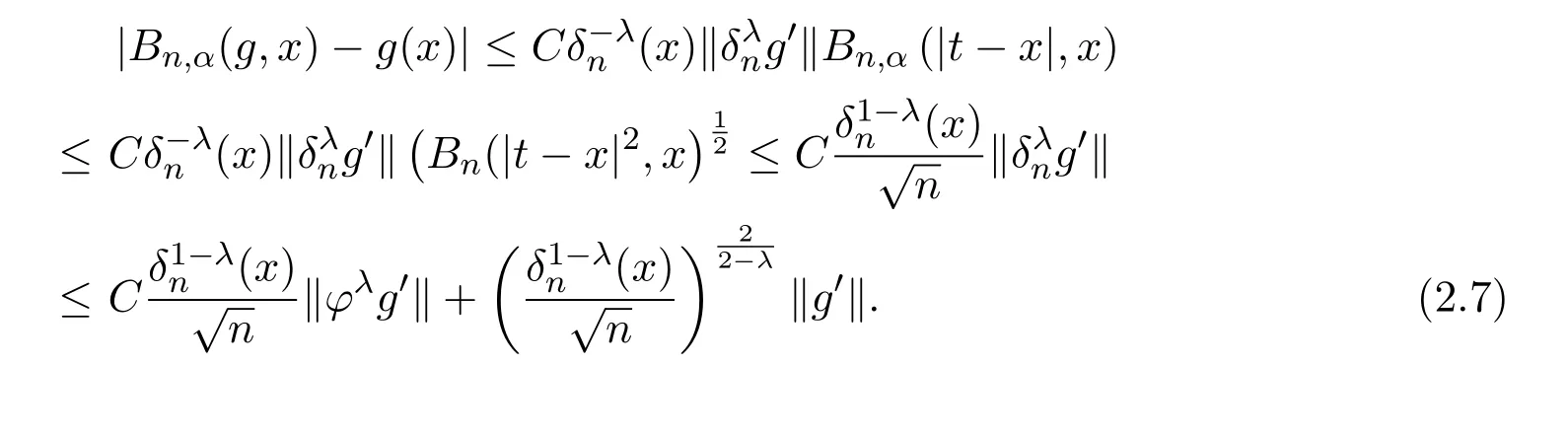
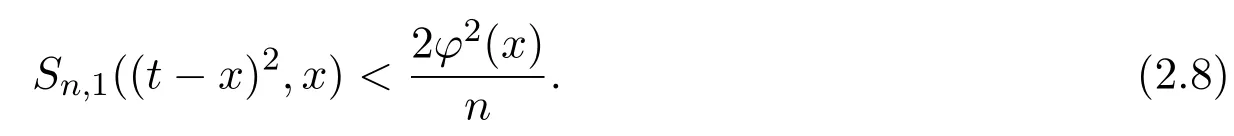
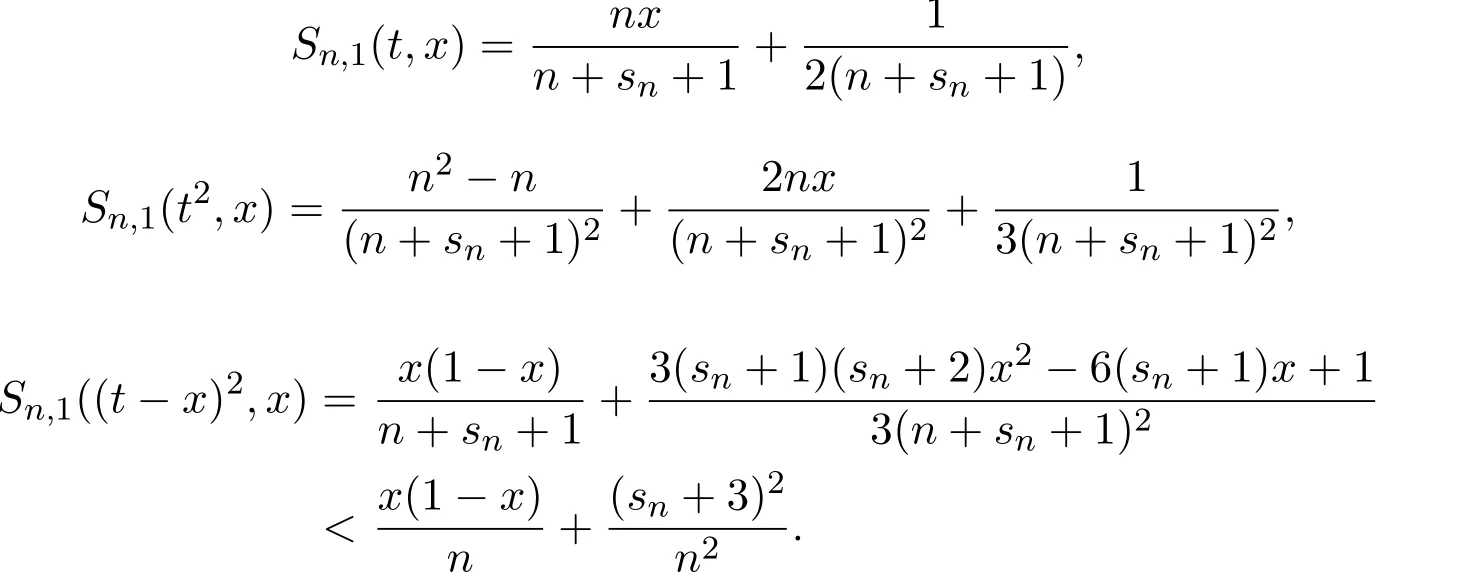
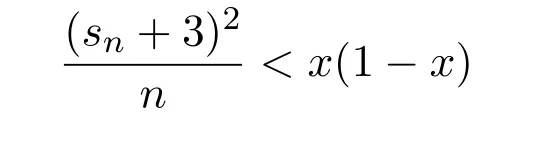
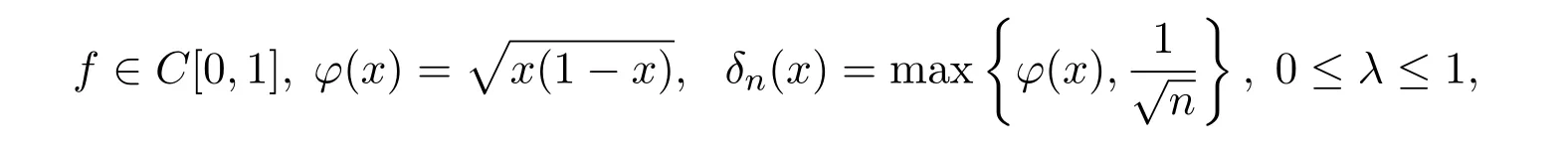
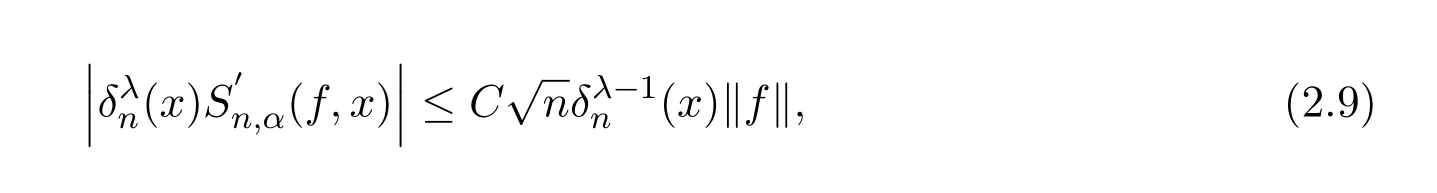

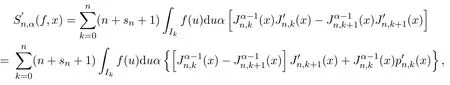
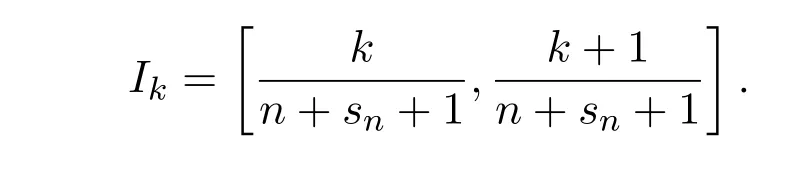
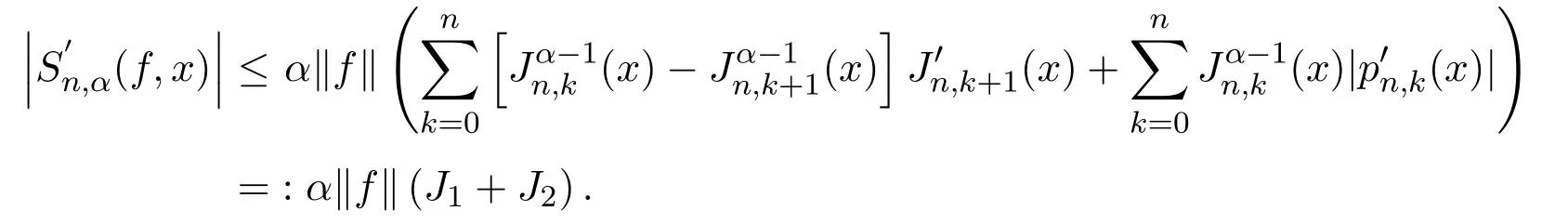
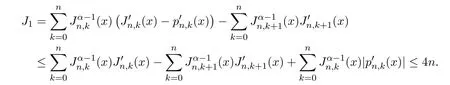
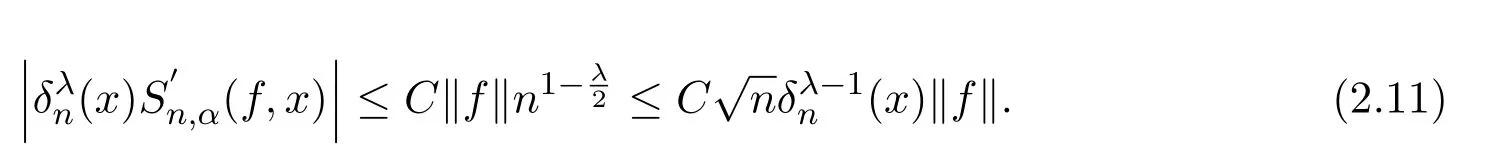
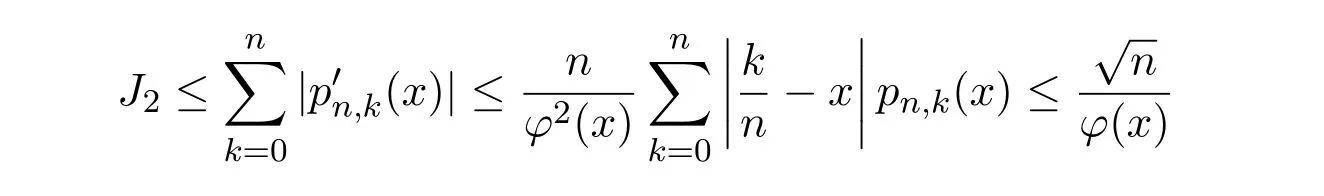
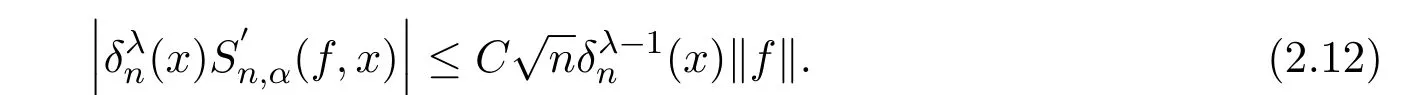
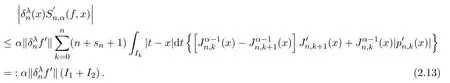
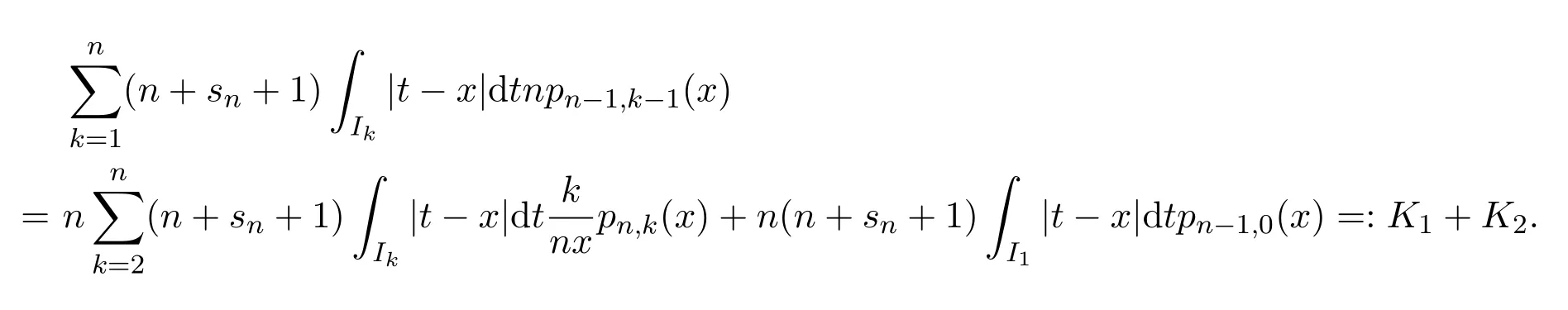
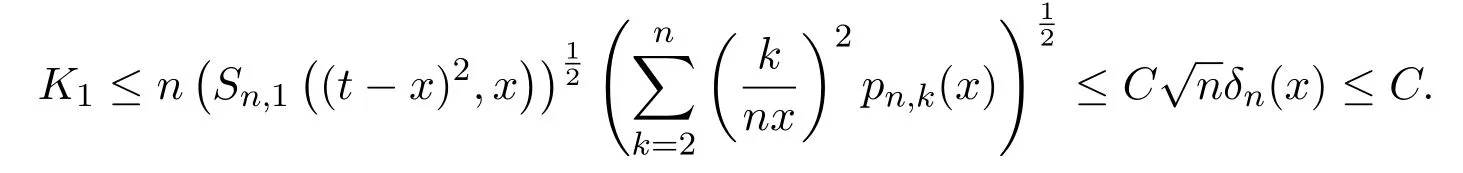
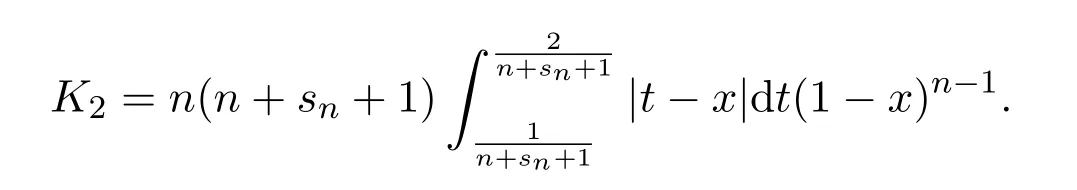
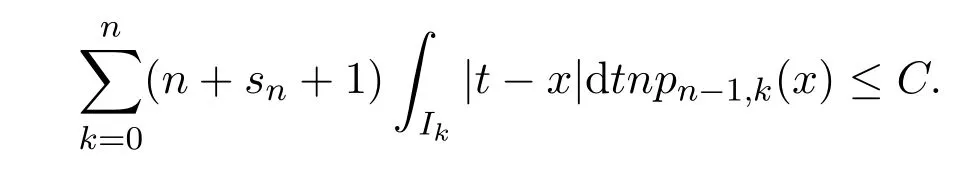

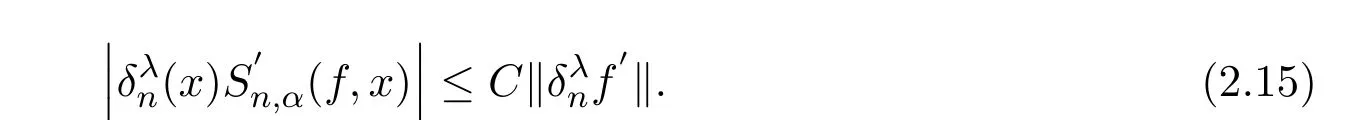

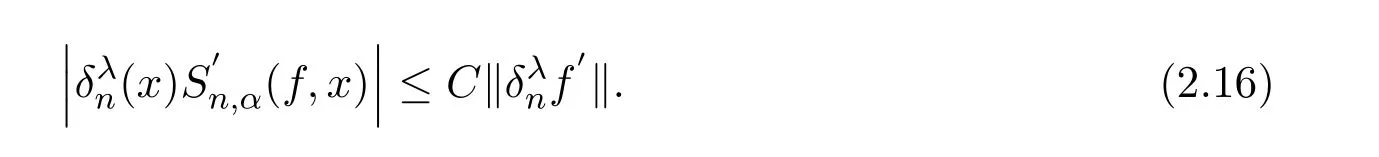
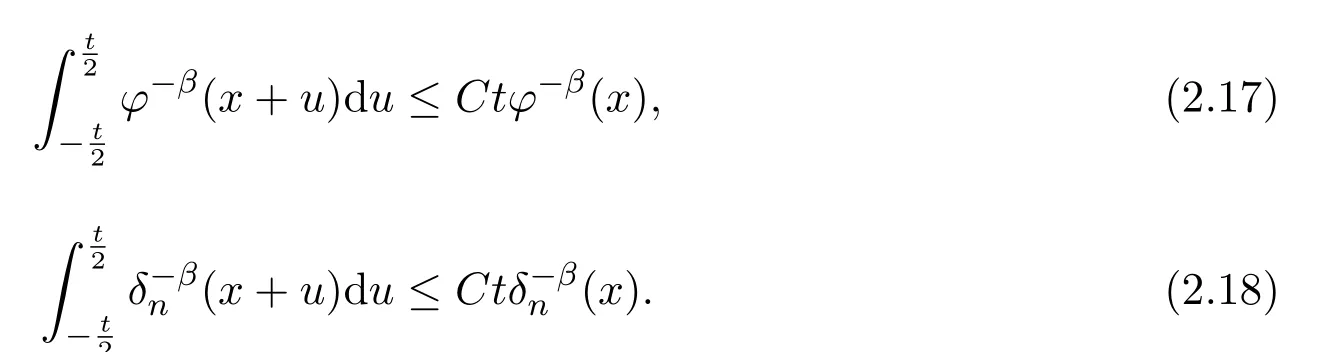
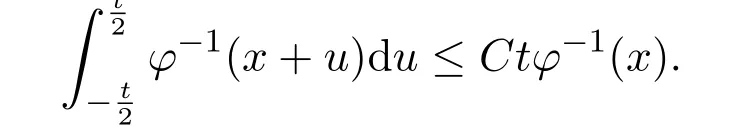
3 定理的证明