斯泽古定理的历史研究
2014-07-18王全来
王全来
(天津师范大学算机与信息工程学院,天津300387)
斯泽古定理的历史研究
王全来
(天津师范大学算机与信息工程学院,天津300387)
探讨幂级数在收敛圆上的行为表现是函数解析开拓的一个重要问题,“具有有限多个不同系数的幂级数”是其研究的重要一类,斯泽古定理即是该类级数研究的一个重要成果.文章基于原始文献,利用历史分析和比较的方法,探讨了斯泽古定理提出的思想背景,法都猜想是其重要的思想来源,详细分析了该定理的形成过程及进一步的发展,对深入理解斯泽古定理的发展历史具有重要作用.
詹逖生;解析开拓;法都猜想;斯泽古定理
探讨幂级数在其收敛圆周上的行为表现是函数解析开拓理论研究中的一个重要课题.具有有限多个不同系数的幂级数的斯泽古定理即是其研究的重要成果之一.关于该定理尽管散见于一些数学理论著作中[1-2],但缺乏从历史角度对该定理的历史做出深入分析.除此之外,国内外也尚未见到关于该定理历史的研究文献.鉴于此,本文基于原始文献,依据历史分析和比较的方法从数学史的角度对具有有限多个不同系数的幂级数的斯泽古定理的历史进行研究,以补现有文献之不足.文章首先分析了该定理提出的历史背景,法都猜想是其重要的思想来源;其次深入分析了该定理的历史发展过程.詹逖生、波利亚、卡尔松和斯泽古等人先后以同样的论文题目《具有有限多个不同系数的幂级数》发表了自己的研究成果.文章对他们的思想方法进行了探讨.最后探讨该定理的进一步发展.
1 斯泽古定理提出的思想背景
三角级数是级数理论研究中的一个重要内容,傅里叶为其做出了重要贡献.他在其著作《热的解析理论》中指出,任意有界的在上定义的函数可以展开形如:的三角级数,其中
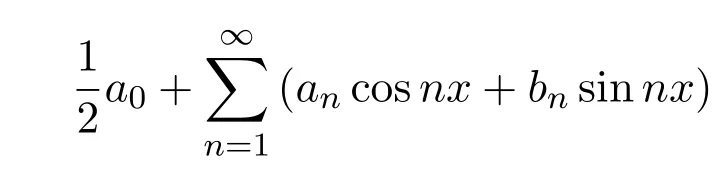

但是,傅里叶对于函数、积分的概念十分模糊,更没有收敛的观念.文献[3]第一次给出给定函数的傅里叶级数收敛并且收敛到本身的充分条件,从而给傅里叶分析奠定了严格基础.文献[4]进一步发展了傅里叶级数理论,并刻画了可用三角级数表示的函数特征.
A0+A1+···+An+···,其中An=ancosnx+bnsinnx级数发散,则总能改变某些An的符号得到一个新级数,在任何区间内存在发散点.利用在区间的点列对此进行证明,并指出泰勒级数以收敛圆为割线,其中他在该文最后猜想,“对于一个泰勒级数的某些系数乘上,总可以得到一个新级数使其以收敛圆为割线,至少当系数满足此页的条件(即上面的条件)时.并且在所有情况下均可发生这种情况.”但可惜的是,法都没有给出证明.正是这一猜想开创了“具有有限多个不同系数的幂级数”理论研究的先河.应当指出,“在所有情况下均可发生这种情况”,从概率角度看,其概率为1.这正是文献[6]的注记中用概率语言强调的“泰勒级数一般以收敛圆为割线”的命题.该命题直到1929年由文献[7]从概率角度给出明确证明.
文献[8]沿着黎曼的思路对法都定理进行了证明.文献[9]又通过构造辅助函数的方法也进行证明,此法比上法简单.尽管如此,并没有对法都猜想进行证明.
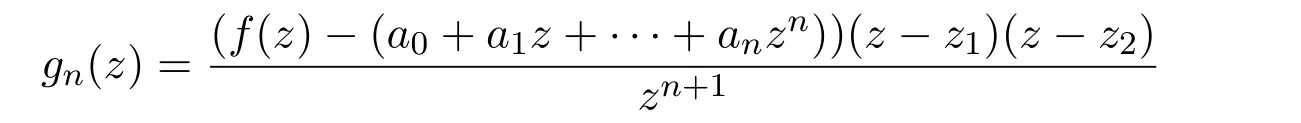
关于法都猜想,首先意识到的是胡尔维茨和波利亚.他们在文献[10]中,对法都猜想进行了证明.波利亚采用聚点法对法都猜想进行证明,而胡尔维茨则给出了另外一种证明方法.他的证明方法如下.设级数P(x)=a0+a1x+a2x2+···+anxn+···收敛半径为1.构造新的级数:
Q(x)=an1xn1+an2xn2+···+anχxnχ+···,
系数anχ全部非0,且满足条件中只出现一次.令

Pε(x)=P0(x)+ε1P1(x)+ε2P2(x)+···+εχPχ(x)+···,
其中ε1,ε2,···,εχ,···只取两个值1和−1.他猜想级数Pε(x)中至少存在一个,其单位圆为自然边界,并用反证法证明了该结论.正是这篇文章深深影响了詹逖生,并由此开始了“具有有限多个不同系数的幂级数”的理论研究.
2 斯泽古定理的历史发展过程
文献[11]对法都猜想继续研究,其主要贡献是研究只有有限多个不同系数的幂级数,并把上述提到的幂级数作为特例.詹逖生对斯泽古定理的形成做出了奠基性工作.
他在该文分五部分对此问题进行讨论.在第一部分给出极点定理,设函数展成的幂级数只具有有限多个不同的系数,且在收敛圆上只有一个极点,则f(x)是具有单重极点的有理函数.系数组(am,···,am−k)的性质在该定理的证明中起到了关键作用.在第二部分给出本性奇点定理,设由级数表示的函数f(x)只具有有限多个不同的系数,有一个奇点η,且在整个平面内单值,则η是一个单位根,且f(x)以η为单重极点.Wigert定理为其证明的重要依据.为了证明主定理和幂级数系数的符号变化定理,他在第三部分把系数组(am,···,am−k)的讨论推广到数组(a1,···,am)性质的讨论,并给出3个相应的辅助定理.
辅助定理2.1在实数系a1
辅助定理2.2设由有限多个数x的正幂和负幂构成的数组,当由x的k1,k2,···,km次幂构成的数组中,所得结果或者是单位根,或者至少出现两次,则x是单位根.
辅助定理2.3设存在一任意数组[z1,z2,···,zn],在辅助定理2.2假设下,zv是单位根.
他关于数组(a1,···,am)性质讨论对其后斯泽古研究该问题有重要影响.
詹逖生在该文的第四部分给出了主定理,也是本文要说明的论点.设只有有限多个不同的系数,用其表示的函数f(x)在单位圆上只有有限多个奇点,且f(x)在一个稍大的圆内是单值的,则f(x)是具有全部单重极点的有理函数,极点即为单位根.他给出的证明如下.由前面定理和辅助定理知,f(x)是在圆|x|=1上只具有单位根的奇点.设m为正素数,则对于一切奇点是一个素的m阶单位根,则m个函数中的每一个具有有限多个不同系数,且在单位圆上只有奇点1,而在稍大的圆内单值.
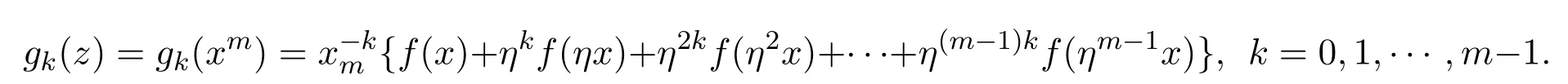

故对于f(x),可有形式多项式+多项式1−xm.
詹逖生的主定理后经其他数学家的努力,使该定理条件和结论更加丰富完善,证明方法更为多样化.
詹逖生在该文第五部分给出了幂级数系数的符号变化定理,并依据上面给出的3个辅助定理进行了证明.设级数通过系数的符号变化得到,且由这两个级数表示的函数在收敛圆上只具有孤立奇点,且在一个稍大的圆内单值,则一个函数在收敛圆上的每个奇点等于另一个函数在收敛圆上奇点与单位根相乘.詹逖生在该文文末指出,在收敛圆上给定的奇点,即在给定的前提条件下,其系数存在一个周期性的符号变化,则其在收敛圆上的奇点可以由此定理推导出.这个结论对其后的波利亚研究该问题有重要影响.
詹逖生和波利亚在数学上有很深的交流,他把这篇论文的设计以通信方式告知了波利亚,因此其思想首先影响到了波利亚.波利亚继续研究该问题,并以另外一种方法得到了詹逖生的主定理.
波利亚在文献[12]中指出,他将以新的方法对詹逖生的论文结果给出依据.在注脚处,他指出,“詹逖生把他的结果以友好的书面方式告知了我,可惜由于交通困难,我既不能了解其证明的细节,也不能查看他的论文的确定文本.我以不完全的方法引用其文还请见谅”.波利亚在该文中得到如下结果.设无穷多项序列:
(1)b0,b1,b2,···,bn,···只有有限多个互不相同;
进一步假设两个幂级数:
(2)a0+a1z+a2z2+···+anzn+···,
(3)a0b0+a1b1z+a2b2z2+···+anbnzn+···,
在单位圆|z|<1内收敛,在圆周|z|=1上只有有限多个孤立奇点,在每个邻域内表示的函数单值,则在圆周|z|=1,(3)的奇点一定可由(2)的奇点与单位根相乘得到.在上述假设下,再补充则序列(1)从某项开始是周期的.当序列(1)从某项开始是周期的,则幂级数b0+b1z+···+bnzn+···是一个只具有简单极点的有理函数,极点即为单位根(E. Landau在1903年解决了“当一个具有有限多个不同系数的幂级数表示一个有理函数时,则从某项开始系数列是周期”的问题).
他采用Wigert定理,阿达玛奇点乘积定理和有理数逼近任意数的方法对上述定理进行了证明.
波利亚在该文最后指出,当幂级数b0+b1z+···+bnzn+···只有有限多个互不相同的系数,且系数不具有周期性,则b0+b1z+···+bnzn+···不满足代数方程,且也不满足线性微分方程的Fuchs类.他利用Wigert定理和反证法证明了该结论.
詹逖生和波利亚的论文出版促使卡尔松关注该问题(应当指出的是,卡尔松已经在1917年《论对于整系数的插值函数和整值函数》中涉及到了斯泽古定理,但当时只是把该定理作为辅助定理使用).在前人基础上,卡尔松在文献[13]中继续研究该问题,并得到了如下一些定理.
定理A设f(x)是具有收敛半径大于等于1的幂级数,在弧的每个点处(包括端点)正则,ε(n)表示随趋于0的收敛函数,当对任意的n,前n项系数中的n(1−ε(n))个只取有限个不同的值,则一定有f(x)其中c是一个常数,g(x)是收敛半径大于1的幂级数.
定理B是收敛半径大于1的幂级数,在单位圆|x|=1上只有有限多个奇点,当对任意的n,前n项系数中的n(1−ε(n))个只取有限个不同的值,则一定有其中P(x)是一个多项式,m是一个整数,g(x)是收敛半径大于1的幂级数.
定理C序列a0,a1,···,an,···只含有限多个不同的值,序列从某项起是周期的,充要条件是幂级数f(x)只有有限多个奇点在单位圆上,且
詹逖生的主定理对应于定理B的特殊情况ε(n)=0.其中f(x)在圆|x|
对该问题认识最深刻,所得结果最为漂亮的是斯泽古,故多数数学学者和数学著作把该结果称为斯泽古定理.他在文献[14]中指出,幂级数f(z)=a0+a1z+a2z2+···+anzn+···只具有有限多个不同的系数,则它或者表示一个有理函数,或者在收敛圆之外不可解析开拓.在第一种情况下,系数an从某项开始是周期的,且其中P(z)表示一个多项式.又可表述为,设在幂级数中不同的系数数是有限的.假设解析函数u(r,x)能够穿过单位圆边界的某个弧解析开拓,则除了某个点外,系数an是一个周期序列的项.
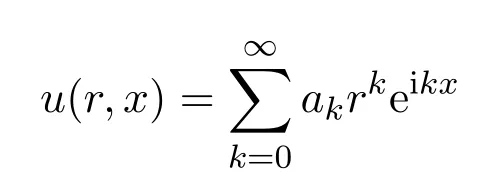
辅助定理3.1对于充分小的δ,当z在曲线Γ(δ)上时,可得到一个不依赖于δ的多项式:
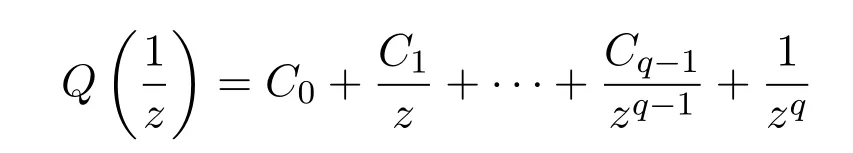
任意小.
辅助定理3.2若解析函数f(z)的幂级数展开为f(z)=a0+a1z+···+anzn+···,其系数有界,在曲线Γ(δ)内和上正则,当zΓ(δ)上时,则

Sn−1(z)为前n−1项和,M是独立于z和n的常数.其中,Γ(δ)是下列区域的边界曲线.
(1)圆弧.|z|=R,φ1≤arcz≤φ2;|z|=1−δ,φ2≤arcz≤φ1+2π.
(2)带型域.1−δ≤|z|≤R,φ1=arcz;1−δ≤|z|≤R,φ2=arcz.其中R>1, 0≤φ1<φ2<2π,δ为任意小的正常数.
他基于两个辅助定理和通过对全部系数群(an,an+1,···,an+q−1),n=0,1,2,···性质的研究,得到了an+v−µ=an,n=µ,µ+1,···,并最终得到

“具有有限多个不同系数的幂级数”在詹逖生、波利亚、卡尔松、斯泽古等人的研究下得到了一个漂亮的定理,并由其后的数学家继续推广.
3 斯泽古定理的进一步发展
在斯泽古之后,数学家们继续研究该问题,并从各个角度对他的漂亮定理进行推广.文献[15]指出函数解析可以转化为函数是有界的.设f(z)其中系数an只取有限多个不同的值.若f(z)在单位圆的某个区域内有界,则f(z)为一个有理函数.利用整函数的模理论、傅里叶积分理论和利普希兹一致收敛定理证明了该定理.文献[16]指出函数解析可以转化为函数是调和的.若调和函数

的复系数ak只取有限个不同的值,且满足增长条件:

则序列{ak}除了脚标的一个有限集外是一个周期序列.利用勒贝格测度理论,Fourier-Stieltjes系数定理及泊松积分证明了该定理.文献[17]证明了如下定理,包含了上述的一些推广.如果

只有有限多个不同的系数,并且对于圆的某个弧(α,β),满足
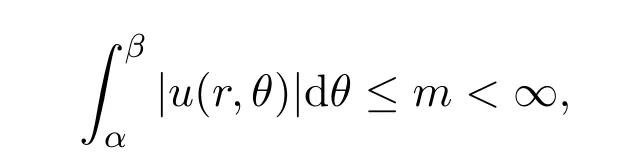
本文基于原始文献梳理了“具有有限多个不同系数的幂级数”的斯泽古定理的历史,剖析了以上学者对该定理的研究思想和方法,由此可以看到数学理论的完善与数学思想方法的进步紧密相关.
[1]Dienes P.The Taylor Series:An Introduction to the Theory of Functions of a Complex Variable[M].London: Oxford University Press,1931.
[2]Titchmarsh E C.The Theory of Functions[M].2nd ed.London:Oxford University Press,1939.
[3]Dirichlet P G L.Sur la Convergence des S´eries Trigonom´etriques[C].Berlin:Springer,1889.
[4]Riemann B.¨Uber die Darstellbarkeit Einer Funktion Durch Einer Trigonom´etrische Reihe[C].Berlin: Springer,1990.
[5]Fauto P.S´eries trigonometriques et s´eries de Taylor[J].Acta.Math.,1906,30:335-400.
[6]王全来.对波莱尔关于“泰勒展开一般以收敛圆为割线”思想研究[J].数学研究与评论,2007,27(4):982-986.
[7]Steinhaus H.¨Uber die Wahrscheinlichkeit daf¨ur,daß der Konvergenzkreis einer Potenzreihe ihre Nat¨urliche grenze ist[J].Math.Zeitschr.,1930,31:408-416.
[8]Steinhaus H.¨Uber Die Wahrscheinlichkeit daf¨ur,daß der Konvergenzkreis einer Potenzreihe ihre Nat¨urliche grenze ist[J].Math.Zeitschr.,1930,31:408-416.
[9]Riesz M.Neuer beweis des Fatouschen satzes[J].G¨ottinger Nachrichten,1916,1:62-65.
[10]Hurwitz A,P´olya G.Zwei beweise eines von herrn Fatou vermuteten satzes[J].Acta.Math.,1916,40: 179-183.
[11]Fauto Jentzsch R.¨Uber potenzreihen mit endlich vielen verschiedenen Koeffizienten[J].Mathematische Annalen,1918,78:276-285.
[12]P´olya G.¨Uber Potenzreihen mit endlich vielen verschiedenen Koeffizienten[J].Mathematische Annalen, 1918,78:286-293.
[13]Carlson F.¨Uber Potenzreihen mit endlich vielen verschiedenen Koeffizienten[J].Mathematische Annalen, 1919,79:237-245.
[14]Szeg¨o G.¨Uber Potenzreihen mit endlich vielen verschiedenen Koeffizienten[C].Berlin:Birkh¨auser Verlag, 1982.557-560.
[15]Duffin R J,Schae ff er A C.Power series with bounded coefficients[J].Amer.J.Math.,1945,67:141-154.
[16]Helson H.Note on harmonic functions[J].Proc.Amer.Math.Soc.,1953,4:686-691.
[17]Helson H.On a theorem of Szeg¨o[J].Proc.Amer.Math.Soc.,1955,6:235-242.
[18]Ilie ffL.Series of Faber polynomials whose coefficients assume a fi nite number of values[J].Dok.Akad. Nauk.SSSR.,1953,90:499-502.
[19]Russev P.A class of analytically uncontinuable series in orthogonal polynomials[J].Math.Ann.,1969,184: 61-64.
The research on the history of the theorem of Szeg¨o
Wang Quanlai
(The College of Computer and Information Engineering,Tianjin Normal University,Tianjin300387,China)
The behavior of power series on the boundary of the disc of convergence is very important to be discussed in holomorphic extension.The power series with only fi nitely many distinct coefficients is signi fi cant for this situation.The theorem of Szeg¨o is important result for power series.This paper discusses the history of this theorem on the basis of historical analysis and literature reviewing.It analyzes it′s background,the procedure and the development.Fatou′s conjecture is its thought origin.
Robert Jentzsch,holomorphic extension,Fatou′s conjecture,Szeg¨o′s theorem
O173.1
A
1008-5513(2014)01-0014-07
10.3969/j.issn.1008-5513.2014.01.003
2008-02-10.
国家自然科学基金(11001199).
王全来(1974-),博士,副教授,研究方向:近现代数学史.
2010 MSC:40A05
