基于组合预测模型的我国入境旅游收入预测研究

郑赤建 张亚昶 向瑶琪

(湘潭大学 旅游管理学院，湖南 湘潭 411105)

一、引言

旅游外汇收入水平是衡量一个国家旅游国际竞争力的重要体现，随着经济全球化与国际交流的深入，我国国际旅游市场发展也越来越成熟，旅游外汇收入从2000年的162.31 亿美元增加到2012年的500.28 亿美元，增加了三倍多，国际旅游收入已然成为我国外汇收入的一个重要来源，这也对我国旅游产业的长足发展起到了推波助澜的作用。与此同时，也推动了对旅游的相关研究，入境旅游收入预测是我国外汇收入预测的一部分，准确而有效的对其进行分析与预测对我国相关部门旅游规划的制定、旅游市场的开拓、旅游形象的宣传、旅游产品的开发等都具有十分重要的指导意义。

目前，对旅游收入预测的研究绝大多数采用的是单一预测方法，然而影响收入的因素很多，单一预测方法往往只能顾及其中的主要因素，并不能涵盖全面有效的信息，因此预测效果会比较差。笔者在已有的文献基础上，采用ARIMA 模型、GM(1，1)灰色预测模型以及回归分析预测模型分别对2000年至2012年入境旅游收入进行定量分析，而后基于误差平方和最小方法构建组合预测模型，并辅以实例进行分析和验证，最后选取精度最高的A－G－R模型作为组合预测模型并进行预测。

二、模型介绍与数据说明

1、模型介绍

(1)ARIMA 模型

ARIMA(p，d，q)模型全称为差分自回归移动平均模型(简记ARIMA 模型)，是由博克思(Box)和詹金斯(Jenkins)于70年代初提出的著名时间序列预测方法，所以又称为Box－Jenkins 模型、博克思－詹金斯法［1］。其中AR 是自回归，p 为自回归项;MA 为移动平均，q 为移动平均项数;d 为时间序列成为平稳时所做的差分次数。ARIMA 模型的基本思想是:将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。

ARIMA 模型是经过d 阶差分变换后的ARMA(p，q)，表示为 ARIMA(p，d，q)。ARIMA 模型的表达式可以用下面的公式表现:

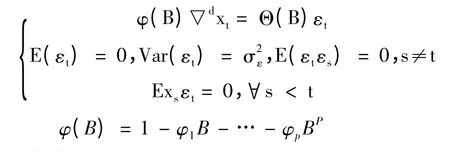
Θ(B)=1－θ1B－…－θqBq分别为p 阶自回归系数多项式，q 阶移动平均系数多项式。

(2)灰色预测模型

灰色预测模型首先是由华中理工大学的邓聚龙教授提出的理论［2］。灰色系统理论通常运用少量已知的白化参数，通过分析、建模、控制和优化等程序，将灰色问题淡化和白化，也就是研究如何利用已知信息(白色)去揭示未知信息(灰色)的问题。在GM(1，1)灰色预测模型中，G 表示grey(灰色)，M 表示model(模型)，GM(1，1)表示1 阶的、1 个变量的模型。其核心是将一组按时间顺序排列的随机上下波动的序列进行累加，生成有规律的数据序列，以微分拟合而建成的预测模型。

(3)回归分析预测模型

回归分析预测法，是在某种现象自变量和因变量之间相关关系的基础上，建立变量之间的回归方程，并将回归方程作为预测模型［3］。根据自变量在预测期的数量变化来预测因变量关系大多表现为相关关系，因此，回归分析预测法是一种重要的预测方法。回归分析预测法有多种类型。依据相关关系中自变量的个数不同分类，可分为一元回归分析预测法和多元回归分析预测法。在一元回归分析预测法中，自变量只有一个，而在多元回归分析预测法中，自变量有两个以上。依据自变量和因变量之间的相关关系不同，可分为线性回归预测和非线性回归预测。

(4)组合预测模型

组合预测法是指对同一个问题，采取二种或二种以上不同预测模型进行预测的方法。它既可以是几种定量方法的组合，也可以是几种定性方法的组合。笔者选择的组合方式是定量方法的组合，即把ARIMA(p，d，q)模型，GM(1，1)灰色预测模型和回归分析预测模型这三种预测方法通过赋予一定的加权系数使它们重新组合起来，形成新的组合预测模型。

组合预测模型可能会产生一个比任何单一预测方法预测值更好的预测值，而且可以减少预测的系统误差，显著改进预测效果［4］。采取组合预测的关键是确定各个单项预测方式的加权系数，而加权系数的确定又有不同的计算方法。笔者在前面提到的三种预测模型基础上，基于误差平方和最小方法，依次求解组合预测模型中各预测模型的权重系数，最终选择最优预测模型。

2、数据说明

笔者研究所要用到的样本数据(表1)均来自于中国国家旅游局官方网站提供的入境旅游年度统计报告。通过表1 可以看出，2003年我国旅游外汇收入与前后两年出现极大的反差，主要是因为2003年3月开始我国出现大范围的“非典疫情”，同时2007年下半年美国爆发次贷危机，并且迅速蔓延至全球各地，也导致接下来两年我国入境旅游人数的减少，这些特殊事件的发生对我国入境旅游收入产生极大的影响，也对模型的预测精度有一定的影响。但考虑到数据真实性，决定不对数据做任何处理，就以表1 提供的数据作为原始数据。在用单一预测模型与各组合预测模型进行预测时，由于篇幅有限，仅列出2011年与2012年的预测值与实际值以供参考，同时对2013年的旅游外汇收入进行预测。

表1 2000－2012年我国入境旅游人数与入境旅游收入一览表

三、单项模型的建立与预测

1、ARIMA 模型的构建与预测

(1)原始序列的平稳性检验

首先对原始时间序列进行平稳性检验。平稳性检验的方法有很多种，但一般采用ADF 单位根检验来精确判断该序列的平稳性。对表1中的数据利用Eviews 软件先进行取对数处理，然后再进行平稳性检验。由检验结果可知原序列不平稳，但是其一阶差分通过检验，并且在1%水平左右显著，为平稳序列。

(2)模型的建立与检验

ARMA(p，q)模型的识别与定阶可以通过样本的自相关与偏相关函数的观察获得，在此利用最佳准则函数(AIC)和SC 准则对模型进行比较，以便从中选择最优模型。由表2 可以看出当p=2，q=3 时，模型的AIC 和SC 的值相对其他二个模型来说要小，因此，选择了ARIMA(2，1，3)作为本次研究的预测模型。

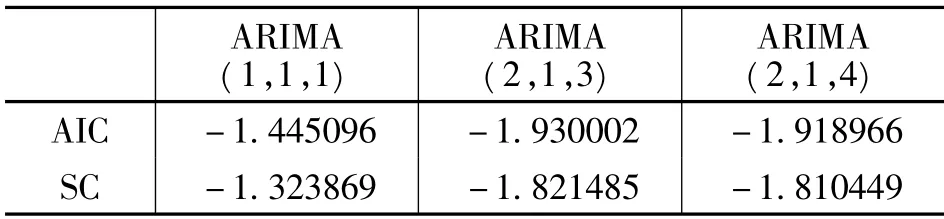
表2 AIC 和SC 准则对多个ARIMA 模型的比较

模型的估计结果是:

在得出预测模型结论之后要对模型进行检验，一般是进行Q 检验。对模型的Q 统计量进行白噪声检验(如图1 所示)，可以得出残差序列相互独立，即为白噪声的概率很大，因此不能拒绝序列相互独立的假设，检验通过。

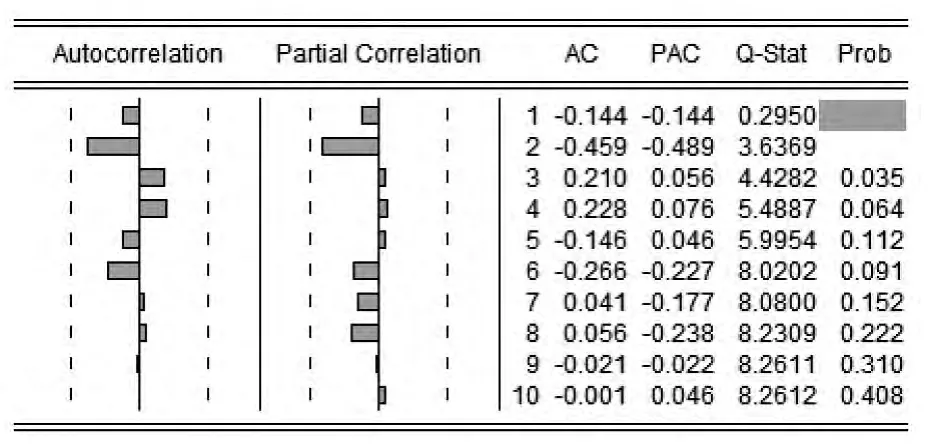
图1 ARIMA(2，1，3)模型的残差图与Q 检验

(3)模型的预测

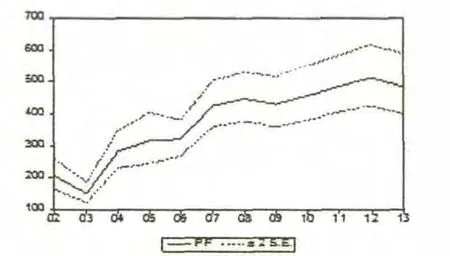
图2 ARIMA(2，1，3)模型的拟合预测图

图2 中实线表示对2002－2012年我国旅游外汇收入的预测值，上下的两条虚线是近似95%的置信区间。利用前面得出的模型对2013年我国旅游外汇收入进行静态预测，最终得到的预测值为485.67 亿美元。由于篇幅有限，下面只提供最近二年内外汇收入预测的预测值与实际值之间的比较，如表3:

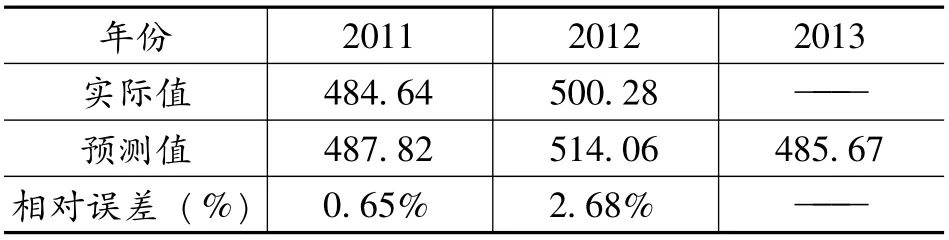
表3 旅游外汇收入的ARIMA(2，1，3)模型部分年份预测表

根据2002－2012年各年份旅游外汇收入预测值与实际值之间的相对误差，最后得出平均相对误差为1.93%。

2、灰色预测模型

(1)GM(1，1)灰色预测模型建模步骤

灰色预测不能直接使用原始时间序列数据，必须对原始数据进行一次累加以便减小数据的原始数据的无规律性和随机性。

原始列:x(0)=［x(0)(1)，x(0)(2)，…，x(0)(13)］，其中x(0)(1)表示2000年的数据，依次类推。

累加列:x(1)(1)=［x(1)(1)，x(1)(2)，…，x(1)(13)］，即对原始列进行一次累加，使数据具有一定的规律性，其中 x(1)(k)。

x(1)(k)的GM(1，1)模型白化形式的微分方程为:

经离散化得:△(1)(x(1)(k+1))

其中△(1)(x(1)(k+1))=x(1)(k+1)－

GM(1，1)灰色模型的基本形式:x(0)(k)+αz(1)(k)=β

α 为发展系数，其大小反应了序列x(0)的增长速度β 为灰作用量，反应数据变化的关系，z(1)(k)为白化背景值，其中:

将(2)、(3)代入(4)得:x(0)(k+1)=

将(5)式展开得:

因此(6)式可以简单的写成:Β=Ν* γ，通过最小二乘法可以求取参数向量γ，即:

将求取的参数代入(1)式，并求出其离散解为:

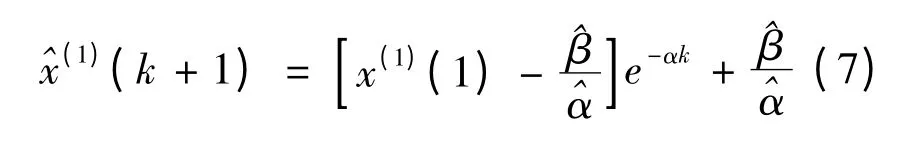
还原到原始数据得:

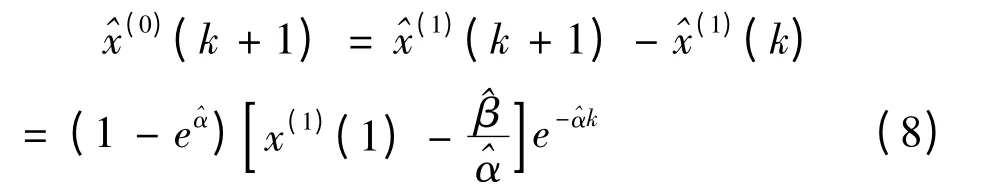
(7)、(8)两式称为GM(1，1)模型的时间相应函数模型，它是GM(1，1)模型灰色预测的具体计算公式。

(2)预测模型的确定

根据上述公式以及表1 中的旅游外汇收入数据，利用excel 软件处理得出参数数值:

α=－0.089853356，β=177.7612618

由此可以得出旅游外汇收入的预测模型为:

(3)模型预测

根据公式(9)、(10)，可以预测出2011－2013年我国入境旅游外汇收入情况，其中对2011年和2012年旅游外汇收入的预测可以与实际值进行比较，以便检验模型的预测精度，2013年外汇收入为预测值，预测结果如表4所示。

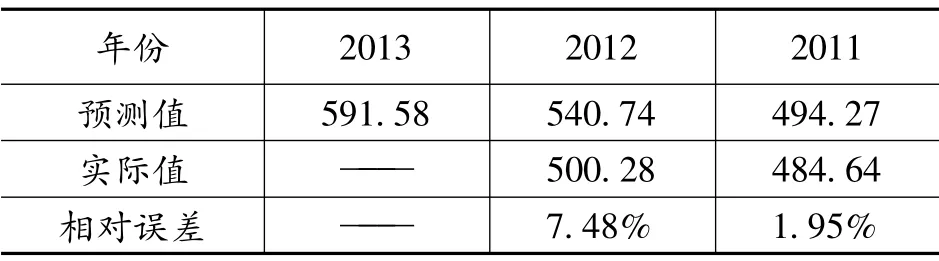
表4 旅游外汇收入的灰色GM(1，1)模型部分年份预测表 (单位:亿美元)

(4)模型检验

对灰色预测模型检验的方法一般包括残差检验、后验差检验以及关联度检验等，由于时间有限在此仅采取残差检验和后验差检验对模型进行检验。利用残差检验最终得出结果如表5 所示。

表5 2000年至2012年各年份的残差——相对误差表

年份 实际收入(亿美元)预测收入(亿美元)相对误差2002 203.85 220.17 8.01%2003 174.06 240.87 38.38%2004 257.39 263.52 2.38%2005 292.96 288.29－1.59%2006 339.49 315.39－7.10%2007 418.93 345.05－17.64%2008 408.43 377.48－7.58%2009 396.75 412.97 4.09%2010 458.14 451.80－1.38%2011 484.64 494.27 1.99%2012 500.28 540.74 8.09%

经计算得出平均相对误差为2.09%，小于5%，残差检验结果通过检验。然后再进行后验差检验，后验差检验的指标为C 值与P 值，其标准对照表如表6 所示。

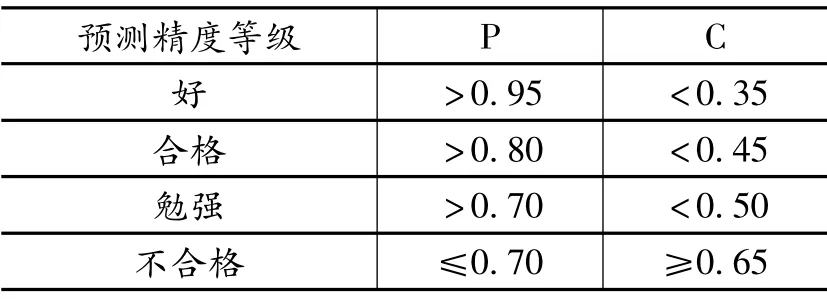
表6 预测精度等级对照表

通过以上两种检验可以得出结论:灰色预测模型具有较高的精度，可以用来预测我国入境旅游外汇收入。

3、回归分析预测模型

(1)根据预测目标确定自变量和因变量

假设旅游外汇收入与我国入境旅游人数存在某种相关关系，因此把我国入境旅游人数(x)看成是自变量，而旅游外汇收入(y)是随着入境旅游人数的变化而相应的变化，因此是因变量。

(2)建立回归预测模型

依据自变量和因变量的统计资料进行计算，在此基础上建立回归分析方程，即回归分析预测模型:y=α+βx。

(3)回归分析及检验

通过Excel 中的回归分析最终确定的回归方程为:^y=0.0625x－395.49，即截距α=－395.47，斜率β=0.0625，相关系数R=0.96，测定系数R2=0.9193，F 值=125.35。R=0.96＞0.553=R0.05，11，F=125.35 ＞4.84=F0.05，11，t=11.196 ＞2.201=t0.05，11，因此通过检验。

回归结果中给出了残差图(见表7)，因此可以计算标准离差。先求出残差的平方:，然后求残差平方和:==15008.31，于是标准离差为:s=，然后可以求得。所以残差的检验结果也是通过的。

表7 预测值以及残差表

(4)确定预测值

利用回归预测模型计算预测值，并对预测值进行综合分析，确定最后的预测值。根据中国旅游研究院的预测2013年我国入境旅游人数预计会达到1.52 亿，那么就以此数据作为自变量x 的值来预测2013年旅游外汇收入y，将15200 代入预测模型^y=0.0625x－395.49 中，得出亿美元。

四、组合预测模型的分析与确定

1、基于误差平方和最小方法的组合预测模型的构建

假设对旅游外汇收入预测问题建立了n 个预测模型，它们对第t年目标变量的拟合值分别为:f1(t)，f2(t)…fn(t);组合预测模型为ft，其中。令J 表示加权平均预测方法的误差平方

R=[1，1，…，1]T，其中，(i，j=1，2，…，n)。则求出使J 取得最小值的非负权重最优组合预测权重向量ω。

2、权重的确定

表8 三种单一预测模型在不同组合预测模型中的权重一览表

3、模型的建立

根据表8 所得到的权重表，可以确定四个组合预测模型的表达式，分别为:CAR=0.76A+0.24R，CGR=0.51G+0.49R，CAG=0.7A+0.3G，CAGR=0.4893A+0.887G+0.2220R。其中Cxx代表不同组合预测模型。

4、误差评价指标比较以及组合模型的确定

为了测定基于误差平方和最小加权的各类组合预测模型的有效性，按照预测效果评价原则，选择误差平方和(SSE)和平均相对误差(MAPE)作为评价指标体系，其中SSE=[6]。表9 列出了这两类误差评价指标体系下各模型的预测效果。

从表9 可以看出，在单项预测模型中，回归分析预测方法的预测效果较差，ARIAM(2，1，3)模型的预测效果最好;从整体上来说，组合预测模型的预测效果要稍微优于单项模型，但并不是所有的组合预测模型都优于单一预测模型，其中ARIAM(2，1，3)和GM(1，1)灰色预测的组合模型的预测效果要明显低于ARIAM(2，1，3)模型的预测效果。无论是SSE 值还是MAPE 值，最小的都是AGR 模型，这说明在这三个单项预测模型以及四个组合预测模型中，AGR 模型的预测效果是最好的，因此可以确定此模型为最优模型，即C=0.4893A+0.2887G+0.2220R。

表9 各类模型误差评价指标比较情况

五、结语

基于误差平方和最小的组合模型预测方法，主要体现了三方面的优势:其一，组合预测综合利用了各单项预测模型所提供的信息，在一定程度上能够减缓随时间推移预测精度降低的趋势;其二，误差平方和最小方法是通过赋予各单一预测模型权重而实现的，因此预测精度要优于传统的组合预测方法;其三，对于三种或者三种以上单一预测模型通过误差平方和最小准则组成新的组合模型至少会有四种，因此组合模型的选择性会更多，而模型之间的比较更有利于预测精度的提高。

入境旅游收入是我国旅游总收入的重要组成部分，对我国旅游业的发展起着至关重要的推动作用。笔者的研究为我国入境旅游收入提供一种新的预测方法，在预测精确度较高的水平下，希望对我国国际旅游市场的发展、相关部门旅游规划的制定、旅游市场的开拓、旅游形象的宣传、旅游产品的开发等方面具有一定的借鉴价值。

［1］石美娟.ARIMA 模型在上海市全社会固定资产投资预测中的应用［J］.数理统计与管理，2005，(1):69－74.

［2］邓聚龙.灰色系统理论教程［M］.武昌:华中理工大学出版社，1990.52.

［3］朱 军.线性模型分析原理［M］.北京:科学出版社，1999.213.

［4］徐国祥.统计预测和决策［M］.上海:上海财经大学出版社.2005.8.

［5］周小我.最优组合预测方法及应用［J］.数理统计与管理，2001，(1):31－32.

［6］刘盛宇，杨桂元，袁宏俊.组合预测模型在我国旅游业预测中的应用［J］.科学决策，2012，(3):28－43.

［7］吴良平，张 健，陆 媛.基于IOWHA 算子的组合在中国入境旅游中的应用分析［J］.旅游学刊，2010，(11):19－27.