球型热载体回转窑褐煤热解过程的传热模型*

2014-06-27王洪亮刘科伟常少英何德民

化学工程师 2014年6期

王洪亮，蒙涛，张华，刘科伟，常少英，何德民

（1.中国石油大学（北京)，北京 102249；2.北京国电龙源环保工程有限公司，北京 100039；3.大连理工大学，辽宁大连 116024）

我国褐煤资源量约3200亿t，目前主要用于发电，但其含水量高达 30（wt）%～50（wt）%导致其发电效率低[1]。褐煤的优势是挥发分含量高达30（wt）%～60（wt）%[2]。褐煤低温热解能获得高附加值的焦油、煤气和半焦，提高褐煤的利用效率。煤热解温度对热解速率及产物分布有显著影响，而传热过程又决定煤热解温度，因此，研究煤热解过程的传热十分必要。胡国新等[3]研究了固定床内煤颗粒的传热，得到了颗粒间总传热系数公式。郭治等[1]建立了以半焦为热载体的褐煤热解过程的传热模型。liu等[4]研究了流化床内煤颗粒的温度分布；Liang等[5]模拟了固体热载体移动床内煤颗粒的温度分布。但未见球型固体热载体（简称热载体球）煤热解过程传热的报道。

本文考虑了反应热及挥发分析出对煤颗粒温度分布的影响，建立了热载体球回转窑煤颗粒热解的传热模型，模拟了煤颗粒的温度分布并分析了影响温度分布的因素。

1 物理模型

热载体球回转窑煤颗粒热解过程及传热途径见图1。

装置额定处理量50kg·h-1，反应器长2.5m，直径0.3m；热载体粒径 12.5mm，密度 2400kg·m3，比热 0.84 kJ·（kg·K）-1，导热系数 10W·（m·K）-1；煤为干燥煤，粒径不大于6mm。高温热载体球与煤在混合器内快速混合后进入反应器，固体物料随反应器转动发生径向混合，轴向上逐渐向反应器出口移动。煤热解产生的气体从固体物料层扩散出并离开反应器。

上述过程的传热途径包括：（1）热载体、煤与反应器壁导热和辐射传热Q1；（2）气流与固体物料层上表面对流换热Q2；（3）热载体球之间的接触和辐射传热 Q3；（4）煤颗粒间的接触和辐射传热 Q4；（5）煤与热解气对流换热 Q5；（6）热载体内导热 Q6；（7）煤颗粒内导热 Q7；（8）热载体与煤接触导热 Q8；（9）热载体与煤辐射传热Q9；（10）热载体与热解气对流换热Q10。其中反应器外壁保温因此忽略物料对反应器壁的传热Q1；物料层上方气流主要来自煤热解，其温度与从固体物料上表面扩散出气体的温度接近，且表面固体物料层占固体物料的比例较小，因此，忽略气流与固体物料层表面的对流换热Q2；在忽略轴向返混的条件下相邻热载体球或煤颗粒之间的表面温差相比于热载体与煤表面温差较小，因此，忽略热载体或煤颗粒之间的接触和辐射传热Q3和Q4；热解气从煤颗粒内部析出，在煤颗粒表面的温度与煤表面温度接近，所以，忽略热解气与煤对流传热Q5。综上所述，该系统主要的传热途径包括Q6～Q10。

2 数学模型

2.1 假设条件

（1）煤颗粒为球体，内部只存在导热；（2）挥发物在煤的内部均匀分布；（3）煤粒形状尺寸不发生变化；（4）煤颗粒与热载体球混合均匀；（5）固体物料无轴向返混。

2.2 固体内部导热

热载体球导热方程如（1）式所示：

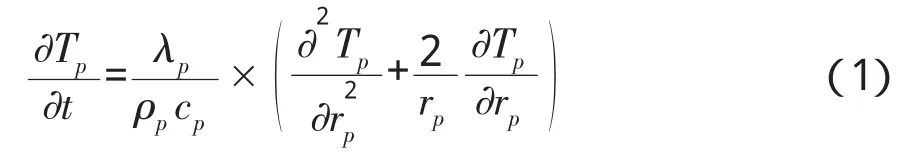
初始条件：

边界条件：

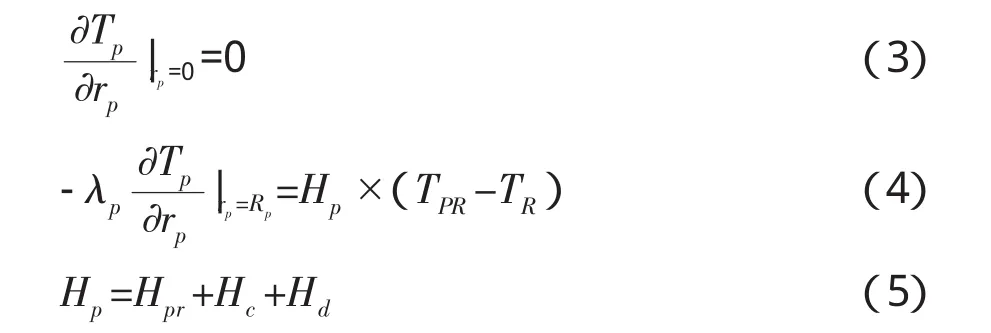
式中 t:时间，s；Rp:热载体半径，m；rp:热载体内部任意处到中心的距离，0≤rp≤Rp，m；TP：热载体内 rp处任意时刻的温度，K；TP0：热载体初温，K；TPR：热载体表面温度，K；TR：煤表面温度，K；λp：热载体导热系数，W·（m·K）-1；ρp：热载体密度，kg·m-3；cp：热载体热容，J·（kg·K）-1。Hp：热载体传热系数，W·（m2·K）-1；Hpr：热载体辐射传热系数，W·（m2·K）-1；Hc：接触传热系数，W·（m2·K）-1；Hd：对流传热系数，W·（m2·K）-1。

煤颗粒内导热方程如（6）式所示：

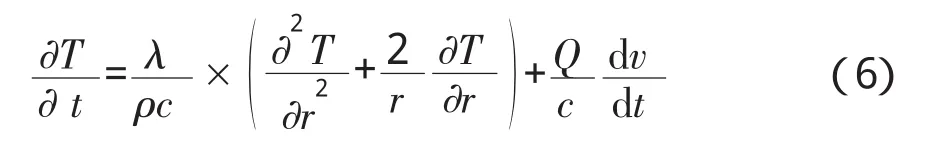
初始条件：

边界条件：

式中 R：煤颗粒半径，m；r：煤颗粒内部任意处到中心的距离，0≤rp≤R，m；T：煤颗粒内r处任意时刻的温度，K；T0：煤初温，K；λ：煤导热系数，W·（m·K）-1[6]；ρ：煤任意时刻的密度，ρ0：煤初始密度，kg·m3；c:煤热容，kJ·（kg·K）-1[6]；v:挥发分产率；H：煤传热系数，W·（m2·K）-1；Hr：煤辐射传热系数，W·（m2·K）-1；Q：单位质量挥发物热解吸热量为837kJ·kg-1[7]。

2.3 辐射传热

热载体与煤辐射传热如（14）式所示[8]：

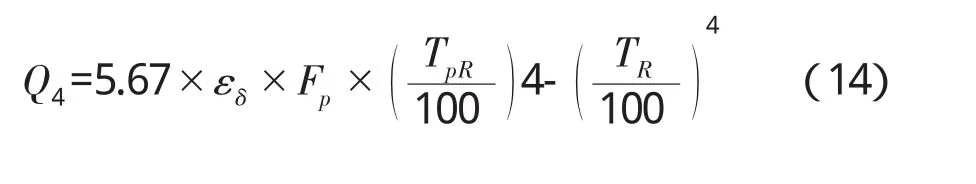
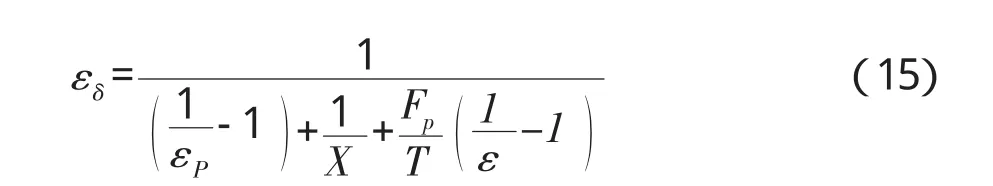
式中 εδ：系统黑度；εp、ε:热载体与煤的黑度分别为0.82和0.8[8]；Fp、F：分别为热载体和煤的表面积，m2；X：辐射角系数，热载体之间和煤颗粒之间的辐射相互抵消，热载体对煤的辐射热量被煤吸收，因此X为1。热载体与煤的辐射换热系数Hpr、Hr分别为

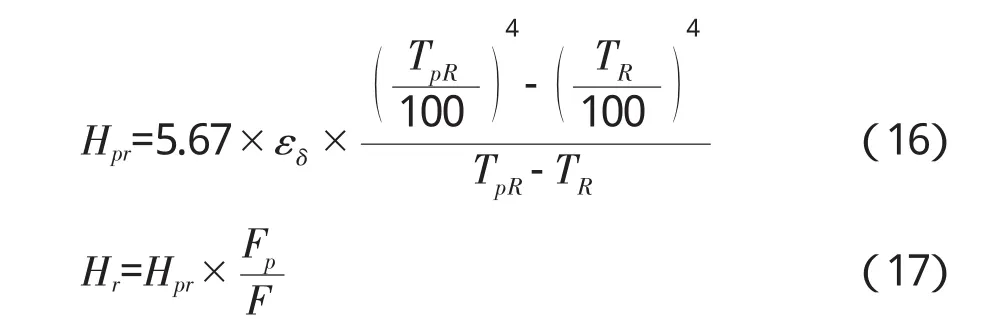
2.4 对流换热

热解气与热载体球的换热为对流换热。固体物料层表面竖直向上平均气速约为0.063m·s-1（按挥发分产率30%；物料层厚度0.1m；空隙率0.2；气体分子量30g·mol-1，温度550℃计算）。当气流速度低于0.15m·s-1时属于自然对流。热载体与热解气对流传热系数按下式计算[8]。

式中 Nu：努谢尔准数；G rg：葛拉晓夫准数；Pr：普朗特准数；h：热载体球最大半周长；δ：气体夹层厚度小于 3.0×10-3m；dp：热载体球直径；λg：气体导热系数0.06W·（m·K）-1；Cp,g：热解气热容 1.1 J·（g·K）-1；μg：气体动力粘度 3.7×10-7kg·（m·s）-1；g为 9.8N·kg-1；β：容积膨胀系数 1.22×10-3K-1；△t：气体与热载体球的温差小于500K；v：气体运动粘度大于3.0×10-7m2·s-1。注：气体参数采用空气相应参数计算。由于挥发分产率低于30%，因此，对流传热系数小于计算结果：

2.5 接触导热

采用Watson等[9]的模型计算接触导热系数如（22）式所示。

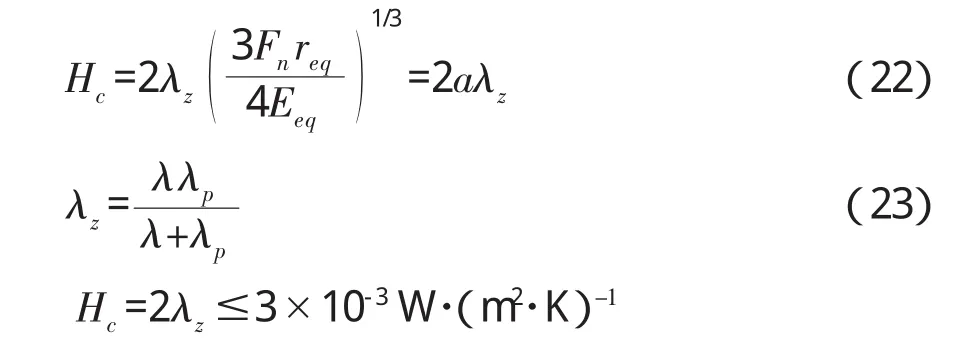
式中 Eeq：有效杨氏模量；req：几何平均半径；Fn：法向应力；a：颗粒接触面半径小于煤颗粒半径<0.003m；λz：热载体与煤复合导热系数。

2.6 褐煤热解

煤热解过程中颗粒密度与反应吸热量为煤挥发分生成速率的函数，因此，需获得煤的热解动力学方程。通常是由煤的热重数据求得动力学参数[1]。但存在3个问题：（1）热重为恒速升温，而热载体对煤加热煤的升温速率随时间变化；（2）热重升温速率与热载体对煤颗粒加热速率相差很大；（3）煤热解动力学参数随升温速率和温度区间发生变化[10]。因此采用热重法直接得到的动力学参数进行计算结果偏差可能较大，但挥发分生成速率可表示为：

式中 d T/d t：煤的升温速率可通过计算迭代获得；d v/d T：挥发分生成速率。为了获得，采用热重分析仪分别以30和50K·min-1的升温速度对褐煤进行热重分析见图2。

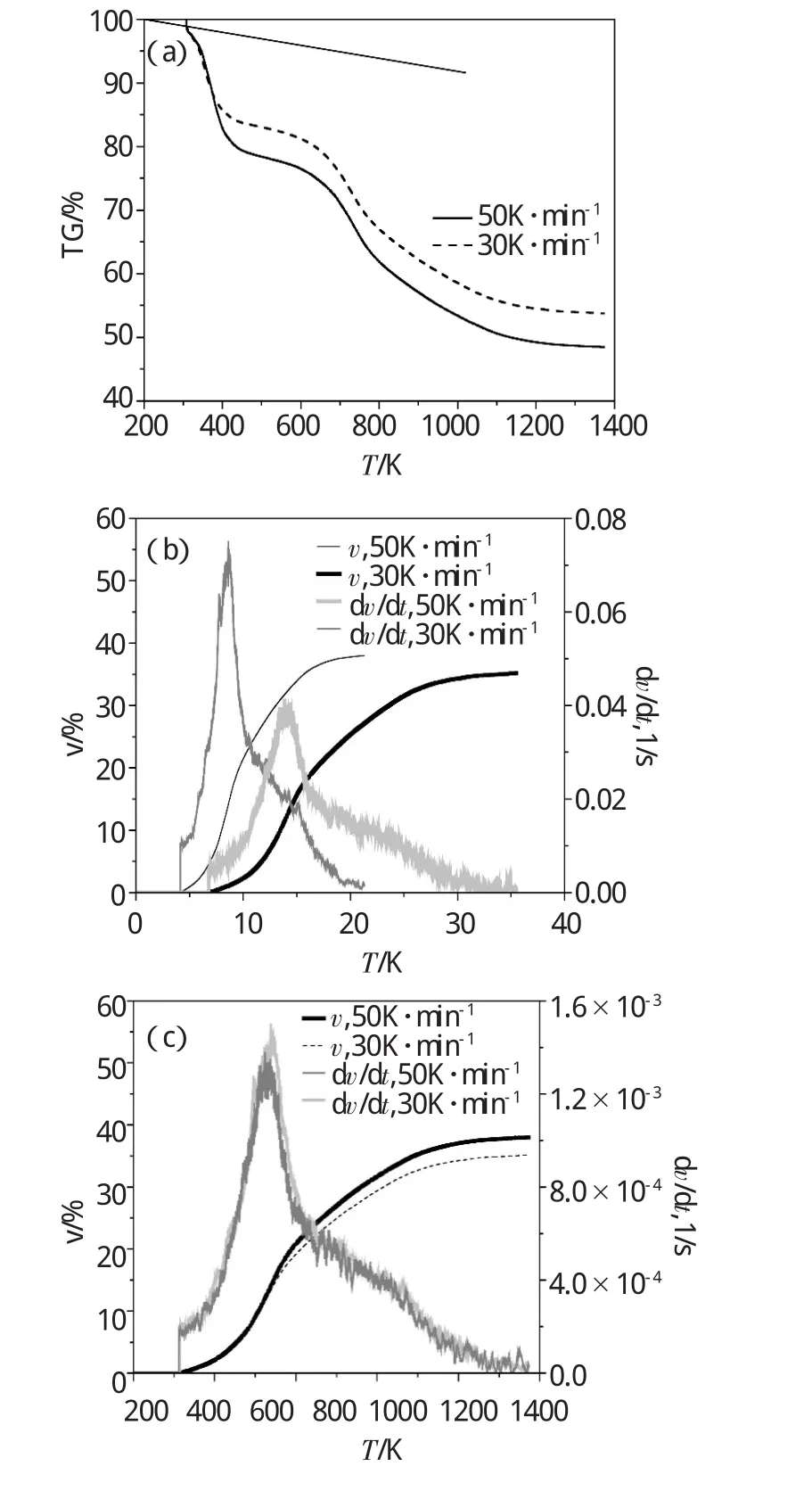
其中，图2（a）为贺斯格乌拉褐煤的TG曲线；图（b）为挥发分生成速率；（c）为挥发分产率随温度的变化。由图2（a）（b）可知虽然不同升温速率下的相差很大，但相同温度下的挥发分产率却很接近，因此，可以根据热重分析获得；图2（d）为对升温速率为50K·min-1的挥发分生成速率曲线拟合，拟合结果如式（24）所示。

4 结果与分析

采用comsol程序计算上述模型。图3为煤颗粒内部的温度分布，热载体和煤初始温度分别为973.15K和373.15K，煤粒径为6mm，热载体与煤质量比为6。

图3 煤颗粒内部温度分布Fig.3 Temperature distribution inside of lignite

由图3可知，热载体温度随时间降低，煤颗粒的温度逐渐升高，约330s后温度达到平衡，约786K。煤颗粒表面温度经5s达到530K，根据热重数据，该煤在515K开始热解，而煤颗粒中心达515K需30s，可见煤颗粒从表面到中心是逐渐开始发生热解。由于煤的导热系数相对较小，在达到平衡温度之前煤颗粒内部存在较宽的温度分布，煤颗粒表面与中心的温差随时间先增大后减小，最大温差约200K；250s后内外温差小于2K。郭治等[1]研究了粒径为20mm的煤颗粒内的温度分布，结果在1800s后颗粒表面与中心的温差约为10K，可见减小煤粒径有助于提高煤的升温速率，实现快速热解。

为了分析煤热解反应热，煤颗粒密度变化以及热解气与热载体对流换热对传热的影响，分别在考虑及未考虑上述因素的条件下模拟了热载体球向煤颗粒的传热。图4为未考虑反应热时煤颗粒内温度分布，条件与图3相同。

图4 未考虑反应热时煤颗粒内部的温度分布Fig.4 Temperature distribution inside of lignitewhen not considering heatof reaction

对比图4和图3可知，热载体球温度降低及煤颗粒温度升高的趋势与图3一致，但达到平衡温度所需的时间约150s，低于考虑反应热条件下的330s；平衡温度约820K比考虑反应热条件下的平衡温度高约34K。上述升温时间延长以及平衡温度降低是由于热载体释放的热量部分用于反应吸热，导致煤颗粒内部发生反应的部位的升温速率降低，使达到平衡温度所需的时间延长。可见不考虑反应热对传热的影响，计算结果将存在较大偏差。

图5为未考虑煤颗粒密度变化时其内部温度分布，条件与图3相同。

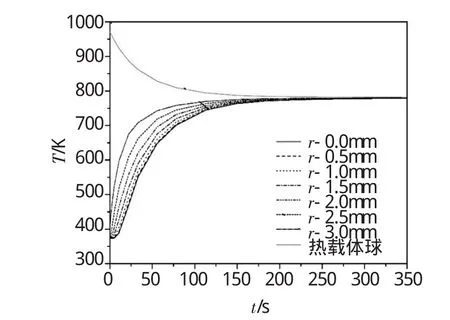
图5 未考虑煤颗粒密度变化时其内部温度分布Fig.5 Temperature distribution inside of lignitewhen not considering particle changing

对比图5和图3可知，在未考虑煤颗粒密度变化的条件下系统的平衡温度约为781K比考虑密度变化条件下低约4K，达到平衡温度所需的时间比考虑密度变化条件下低约5s。这是由于煤在升温过程中当温度达到热解温度后，挥发分开始从煤颗粒内部析出，挥发分的析出导致煤颗粒密度减小，煤颗粒密度变小使得系统的平衡温度升高，也使得达到平衡温度所需的时间略有缩短。虽然在780K煤的挥发分产率约为20%，但密度的变化对平衡温度的影响却相对较小。这是由于煤颗粒随温度升高从表面到中心逐渐发生反应，煤颗粒密度逐渐减小而非陡然减小，未热解的有机物仍然吸收热量，因此煤颗粒密度的变化对平衡温度以及平衡时间的影响不大。

图6为未考虑热解气对流换热时煤颗粒内部温度分布，条件与图3相同。

图6 未考虑热解气对流换热时煤颗粒内温度分布Fig.6 Temperature distribution inside of lignitewhen not considering heat convection of pyrolysis gas

在煤热解过程中，当煤颗粒温度达到热解温度后，煤中挥发分热解从煤颗粒内部析出形成热解气。热载体表面的温度比热解气的温度高，当热解气流经热载体表面时与热载体表面进行对流换热，带走部分热量引起煤颗粒的温度变化。对比图6和图3可知，在未考虑热解气对流换热的条件下系统的平衡温度约为790 K比考虑热解气对流换热变化条件下低约4 K，达到平衡温度所需的时间比考虑热解气对流换热条件下低约5 s。表明热解气与热载体球表面的对流换热对传热的影响较小。