Hosoya指数第二小、第三小的双圈图

李 莎，卓玛措，王 微

（1.青海师范大学数学系，青海西宁810008；2.唐山市第四十九中学，河北唐山063000）

Hosoya指数第二小、第三小的双圈图

李 莎1，卓玛措1，王 微2

（1.青海师范大学数学系，青海西宁810008；2.唐山市第四十九中学，河北唐山063000）

双圈图是边数等于点数加1的连通图.一个图的Hosoya指数是这个图的所有匹配的个数.在已有结论的基础上通过加边，并利用求指数的删边、删点公式，刻画了具有m－匹配的Hosoya指数第二小、第三小的双圈图.

Hosoya指数；m－匹配；双圈图

关于图的Hosoya指数是H.Hosoya在1971年提出的，它是组合化学的拓扑指标中的一个突出例子，也是目前研究的热点之一.［1－7］这里考虑的所有图均是有限、简单、无向图，没有定义的概念和术语，参见文献［8］.对于一个图G，我们用V（G）表示它的点集，E（G）表示它的边集.G中的两条边若不相邻，则称这两条边是独立的.G中k个相互独立的边组成的集合称为G的一个k－匹配.用Z（G）表示G的匹配的个数，则其中m（G，k）表示G的k－匹配的个数，并且m（G，0）＝1，m（G，1）＝｜E（G）｜.容易看出，若m（G，k）＝0，则m（G，k＋1）＝0（k≥2）.并且些刻画Hosoya指数极图的文献，主要刻画了给定的几类图－树，涉及四边形、六圈的特定结构的图［5，9－13］.文献［14］刻画了具有m－匹配的Hosoya指数最小及第二小的树.文献［15］刻画了具有m－匹配的Hosoya指数最小和第二小的单圈图，及具有m－匹配的Hosoya指数最小的双圈图.文献［16］刻画了具有m－匹配的Hosoya指数第三小至第六小的单圈图.而我们刻画了具有m－匹配的Hosoya指数第二小、第三小的双圈图.

1 预备知识

令M表示G的一个匹配，若v与M中一条边关联，则称v是M饱和的，记为v∈M；否则称为M不饱和的，记为v∉M.如果G中所有点均是M饱和的，则称M是G的一个完美匹配.如果不存在G中的一个匹配M′，满足｜M′｜＞｜M｜，则称M是G的最大匹配.显然，完美匹配一定是极大匹配.我们用α′（G）表示G的最大匹配｜M′｜＞｜M｜的边数.令U（n，m）表示α′（G）＝m点数为n的单圈图.B（n，m）表示α′（G）＝m点数为n的双圈图.

若W⊆V（G），我们用G－W表示删掉W中的点及与这些点关联的边的G的子图.类似的，如果E′⊆E（G），用G－E′表示删掉E′中的边的G的子图.如果W＝v，并且E′＝｛xy｝，我们用G－v，G－xy分别代替G－｛v｝，G－｛xy｝.对于图G的一个点v，令NG（v）＝｛v｝∪｛u｜uv∈E（G）｝.

引理1［14］令G表示一个图，并且v∈V（G），令v1，v2，…，vk是v的邻点，则

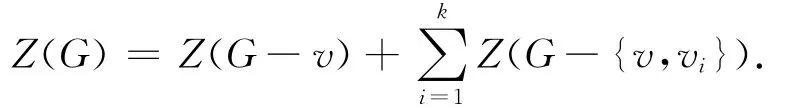
引理2［14］令G表示一个图，并且uv表示G的一条边，则

推论1 令G表示一个图，如果u∈V（G）是G的一个悬挂点，并且v是u的唯一的邻点，则

引理3［14］令G表示具有k个分支G1，G2，…，Gk的图，则

图1 一些具有m－匹配的单圈图和双圈图

引理4［14］令Pn和Sn表示含有n个点的路和星，则对于含有n个点的所有树T，我们有

这里fn是第n个Fibonacci数，并且f0＝0，f1＝1.

引理5 令G表示一个图，G1是G的子图，则Z（G）≥Z（G1）.并且若｜E（G1）｜＜｜E（G）｜，则

因为G1的每一个匹配也是G的匹配，从而引理5显然成立.

引理6 令T是一个树，α′（T）＝k（k≥1），并且T≇lK1∪kK2（l≥0），则Z（T）≥5·2k－2等号成立当且仅当T≅P4∪（k－2）P2∪l′（k1）（l′≥0）.

引理7［15］G∈U（n，m）（n≥2m，m≥4），则Z（G）≥2m－2（2n－3m＋4）等号成立当且仅当G≅U1（n，m）（如图1）.

引理8［15］令G∈U（n，m）（n≥2m，m≤4），G≇U1（n，m）.则Z（G）≥2m－4（10n－15m＋13）等号成立当且仅当G≅U2（n，m）（见图1）.

引理9［16］令G∈U（n，m）（n≥2m，m≥4），G≇｛U1（n，m），U2（n，m）｝，则Z（G）≥2m－4（10n－15m＋14）等号成立当且仅当G∈｛U3（n，m），U7（8，4），U10（10，5）｝.

引理10 令T是一个树，α′（T）＝m（m≥1），并且T≇｛（n－2m）K1∪mK2，P4∪（m－2）K2∪（n－2m）K1｝，则Z（T）≥3×2m－1等号成立当且仅当T≅｛T3，T5｝（见图2）.若还有其他含有m个匹配的图，以图2中9个图中的一个作为子图，则T3，T5在m≥4中是第三小的图.

图2 一些包含若干K1和K2的具有m－匹配的图

引理11［15］令G∈B（n，m）（n≥2m，m≥4），则Z（G）≥2m－2（2n－3m＋5）等号成立当且仅当G≅B1（n，m）（见图1）.

2 主要结果及证明

定理1 令G∈B（n，m），G≇B1（n，m）（n≥2m，m≥4），则Z（G）≥2m－4（10n－15m＋18）等号成立当且仅当G∈｛B2（n，m），B7（8，4）｝.

证明 令G∈B（n，m）（n≥2m，m≥4），并且M是G的一个m－匹配，我们总能从G的圈中找出一条边uv，使得uv∉M，则G－uv是一个连通单圈图.此外，α′（G－uv）＝m（因为G－uv是G的一个子图，由引理5有α′（G－uv）≤α′（G）＝m，注意到M是G－uv的一个m－匹配，我们有α′（G－uv）≥m，因此α′（G－uv）＝m，G－uv∈U（n，m）.现在分以下三种情况讨论：

（1）G－uv≅U1（n，m），并且G≇B1（n，m），则G∈｛B2（n，m），G1，G2，G3，G4，G5，G6，G7｝（见图1），由引理1直接计算，得：

因此，Z（Gi）＞Z（B2（n，m）），1≤i≤7.

（2）G－uv≇U1（n，m），并且G≇B1（n，m），由引理8，Z（G－uv）≥2m－4（10n－15m＋13）等号成立当且仅当G－uv≅U2（n，m）.注意到G－｛u，v｝有（m－2）－匹配，所以有Z（G－｛uv｝）≥2m－2等号成立当且仅当G－｛u，v｝≅（n－2m＋1）K1∪（m－2）K2，易看出uv中必有一个点是U2（n，m）中的一个（n－m）度点，另一个是U2（n，m）中的一个3度点，这种情况是不可能的.由引理6，若Z（G－｛u，v｝）≥5·2m－4等号成立当且仅当G－｛u，v｝≅（m－4）K2∪P4∪（n－2m＋2）K1.由引理2，

等号成立当且仅当G－uv≅U2（n，m），并且G－｛u，v｝≅（m－2）K2∪P4∪（n－2m＋2）K1.易看出u，v中的一个点是U2（n，m）中的一个（n－m）度点，另一个是一个邻接于U2（n，m）中的一个2度点的悬挂点.因此等号成立当且仅当G≅B2（n，m）.

（3）G－uv∉｛U1（n，m），U2（n，m）｝，如果m＝4，n＝8，则

并且

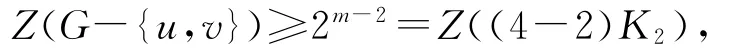
所以

等号成立当且仅当u，v的两个点在U7（8，4）中为3度点.因此等号成立当且仅当G≅B7（8，4）.如果m＝5，n＝10，则Z（G－uv）≥Z（U10（10，5）），并且Z（G－｛u，v｝）≥25－2＝23＝Z（（5－2）K2），

等号成立当且仅当G－uv≅U10（10，5），且G－｛u，v｝≅3 K2.此时G不可能是m＝5时，Hosoya指数第二小的图.

当G－uv∉｛U1（n，m），U2（n，m），U7（8，4），U10（10，5）｝，由引理9，Z（G－uv）≥2m－4（10n－15m＋14）等号成立当且仅当G－uv≅U3（n，m）.注意到G－｛u，v｝有（m－2）－匹配，所以有Z（G－｛u，v｝）≥2m－2等号成立当且仅当G－｛u，v｝≅（n－2m＋2）K1∪（m－2）K2.从而

等号成立当且仅当G－uv≅U3（n，m），而且G－｛u，v｝≅（m－2）K2∪（n－2m＋2）K1.此时，uv的一个端点必是U3（n，m）的一个（n－m）度点，另一个是邻接于一个3度点的2度点，此时Z（G）≥Z（B2（n，m））.综上，定理得证.

定理2 G∈B（n，m），G∉｛B1（n，m），B2（n，m），B7（8，4）｝（n≥2m，m≥4），则

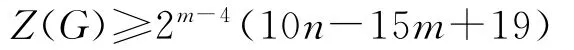
等号成立当且仅当G∈｛G2，B3（n，m），B10（10，5），B12（12，6），B11（13，5）｝.

证明 G∈B（n，m）（n≥2m，m≥4），使得G≇｛B1（n，m），B2（n，m），B7（8，4）｝，并且M是G的一个m－匹配，我们总能从G的一个圈中选出一条边uv，使得uv∉M，则G－uv是一个n度点的连通单圈图，并且α′（G－uv）＝m（因为G－uv是G的一个子图，由引理5我们有α′（G－uv）≤α′（G）＝m，注意到M是G－uv的一个m－匹配，我们有α′（G－uv）≥m，因此α′（G－uv）＝m）.现在分以下4种情况讨论：

（1）G－uv≅U1（n，m），并且G≇｛B1（n，m），B2（n，m），B7（8，4）｝，由定理1，有

（2）G－uv≇U1（n，m），并且G≇｛B1（n，m），B2（n，m），B7（8，4）｝，由引理8，有

等号成立当且仅当G－uv≅U2（n，m）.注意到G－｛u，v｝有（m－2）－匹配，我们再分3种情况讨论：

ⅰ.若G－｛u，v）≅（m－2）K2∪（n－2m＋2）K1，Z（G－｛u，v｝）＝2m－2，则容易看出uv的一个端点是U2（n，m）的一个（n－m）度点，并且uv的另一个端点是U2（n，m）的一个3度点.显然，这是不可能的.

ⅱ.若G－｛u，v｝≅（m－4）P2∪P4∪（n－2m＋2）K1，Z（G－｛u，v｝）＝5·2m－4，因此G≅B2（n，m）.矛盾.

ⅲ.由引理10，我们有Z（G－｛u，v｝）≥3·2m－3等号成立当且仅当G－｛u，v）≅｛T3，T3｝（见图2）.因此，如果G－｛u，v｝≅T5，那么

但P5是T5的子图，并且U2（n，m）中的子图P5必以U2（n，m）的（n－m）度点为点，从而若u，v中有点是（n－m）度点，则G－｛u，v｝中不可能有T5.若v中没有点是（n－m）度点，则G－uv≅U2（n，m），从而矛盾.如果G－｛u，v｝≅T3，那么

等号成立当且仅当uv的一个端点是U2（n，m）的（n－m）度点，另一个端点是邻接于一个3度点的悬挂点，从而Z（G）≥Z（G2）.

（3）G－uv≇｛U1（n，m），U2（n，m）｝，此时Z（G－uv）≥2m－4（10n－15m＋14）等号成立当且仅当G－uv≅U3（n，m）.又G－｛u，v｝中有（m－2）－匹配，Z（G－｛u，v｝）≥2m－2等号成立当且仅当G－｛u，v｝≅（m－2）K2∪（n－2m＋2）K1.此时，u，v中必有一个端点是（n－m）度点，另一个是邻接于一个3度点的2度点，此时G≅B2（n，m），矛盾.从而Z（G－｛u，v｝）≥5·2m－4等号成立当且仅当G－｛u，v｝≅（m－4）P2∪P4∪（n－2m＋2）K1.此时，

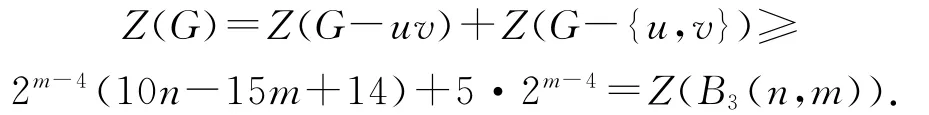
当m＝4，n＝8，则Z（G－uv）≥Z（U7（8，4）），此时G－｛u，v｝中有2－匹配，从而｛G－｛u，v｝｝≥22.矛盾.若G－｛u，v｝≅P4∪2k1，此情况不可能.当G－｛u，v｝≅｛T3，T5｝，此情况也不可能.当m＝5，n＝10，则Z（G－uv）≥Z（U10（10，5）），并且G－｛u，v｝中有3－匹配.

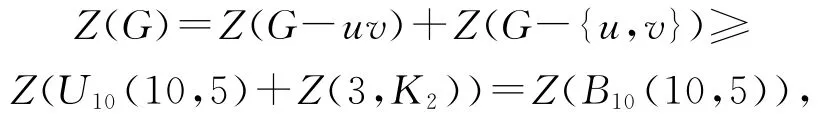
等号成立当且仅当G≅（B10（10，5））.

（4）G－uv≇｛U1（n，m），U2（n，m），U3（n，m），U7（8，4），U10（10，5）｝，此时Z（G－uv）≥2m－4（10n－15m＋15）等号成立当且仅当G∈｛U4（n，m），U5（n，m）｝，并且G－｛u，v｝中有（m－2）－匹配，Z（G－｛u，v｝）≥2m－2等号成立当且仅当G－｛u，v）≅（m－2）K2∪（n－2m＋2）K1.

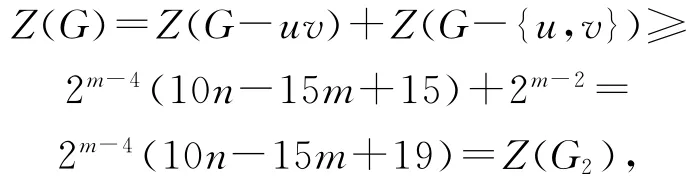
等号成立当且仅当G－uv≅U4（n，m）且G－｛u，v｝≅（m－2）K2∪（n－2m＋2）K1，或G－uv≅U5（n，m）且G－｛u，v｝≅（m－2）K2∪（n－2m＋2）K1.此时易得Z（G）≥Z（G2），并且容易证出B12（12，6），B11（10，5）也是Hosoya指数第三小的图.

［1］ HOSOYA H.Topological index，a newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons［J］.Bull Soc Jpn，1971，44：2332－2339.

［2］ CYVIN S J，GUTMAN I.Hosoya index of fused molecules［J］.MATCH Commun Math Comput Chem，1988，23：89－94.

［3］ CYVIN S J，GUTMAN I，KOLAKOVIC.Hosoya index of some polymers［J］.MATCH Commun Math Comput Chem，1989，24：105－117.

［4］ GUTMAN I.On the Hosoya index of very large molecules［J］.MATCH Commun Math Comput.Chem，1988，23：95－103.

［5］ GUTMAN I.Extremal hexagonal chains［J］.J Math Chem，1993，12：197－210.

［6］ GUTMAN I，POLANSKY O E.Mathematical concepts in organic chemistry［M］.Berlin：Springer，1986：1－228.

［7］ TURKER L.Contemplation on the Hosoya indices［J］.J Mol Struct（Theochem），2003，623：57－77.

［8］ BONDY J A，MURTY U S.Graph theory with applications［M］.Amsterdam：North－Holland，1976：1－264.

［9］ ZHANG L Z.The proof of Gutman's concerning extremal hexagonal chains［J］.J Sys Sci Math Scis，1998，18：460－465.

［10］ ZHANG L Z，TIAN F.Extremal hexagonal chains concerning largest eigenvalue［J］.Sciences in China：Series A，2001，44：1089－1097.

［11］ ZHANG L Z，TIAN F.Extremal catacondensed benzenoids［J］.J Math Chem，2003，34：111－122.

［12］ 唐保祥，任韩.4类图完美匹配数目的解析式［J］.东北师大学报：自然科学版，2013，45（3）：20－24.

［13］ 马海成，李生刚.图的多项式与Hosoya指标［J］.东北师大学报：自然科学版，2013，45（4）：41－44.

［14］ HOU Y P.On acyclic systems with minimal Hosoya index［J］.Discrete Appl Math，2002，119：251－257.

［15］ YU A M，TIAN F.A kind of graphs with minimal Hosoya indices and maximal Merrifield－Simmons indices［J］.MATCH Commun Math Comput Chem，2006，55：103－118.

［16］ YE C F.Unicyclic graphs with the third smallest to sixth smallest Hosoya index［J］.MATCH Communications in Mathematical and in Computer Chemistry，2012，55：593－604.

Bicycle graphs with the second and third Hosoya index

LI Sha1，ZHUOMA Cuo1，WANG Wei2
（1.Department of Mathematics，Qinghai Normal University，Xining 810008，China；2.Tangshan No.49Middle School，Tangshan 063000，China）

Bicycle graphs are connected graphs with m＝n＋1，where mdenotes the number of edges and ndenotes the number of vertices.The Hosoya index of a graph G，denoted by Z（G），is defined as the total number of matchings（independent edge subsets），including the empty edge set，of a graph.On the basis of the existing conclusions，we characterize the bicycle graphs with the second and third Hosoya index with m－matching by adding edges and using known formulas.

Hosoya index；m－matching；bicycles

O 157.5 ［学科代码］ 110·7470

A

（责任编辑：陶 理）

1000－1832（2014）02－0045－06

10.11672／dbsdzk2014－02－010

2013－12－16

国家自然科学基金资助项目（11161037；11101232）.

李莎（1988—），女，硕士研究生，主要从事图论及其应用研究.