左截断右删失数据下几何分布参数的点估计

何朝兵，刘华文

（1.安阳师范学院数学与统计学院，河南安阳455000；2.山东大学数学学院，山东济南250100）

左截断右删失数据下几何分布参数的点估计

何朝兵1，刘华文2

（1.安阳师范学院数学与统计学院，河南安阳455000；2.山东大学数学学院，山东济南250100）

证明了左截断右删失数据下几何分布参数极大似然估计的存在唯一性，给出了由EM算法得到的参数的迭代公式，进行了随机模拟试验，结果表明参数的MLE和EM估计的精度都较高.

左截断右删失；几何分布；极大似然估计；EM算法；随机模拟

几何分布是一种很重要的离散型寿命分布，它是指数分布的离散化，是特殊的离散型威布尔分布，在排队论和可靠性数学等分支中有着很广泛的应用.文献［1－6］对一般截尾寿命试验下几何分布的参数进行了统计分析.近些年来，对左截断右删失数据的研究比较多，文献［7－13］深入研究了被观察变量是连续型分布的情况，但还没有文献涉及几何分布的情况.本文首先证明了左截断右删失数据下几何分布参数极大似然估计的存在唯一性，然后给出了由EM算法得到的参数的迭代公式，最后进行了随机模拟试验，结果表明参数的MLE和EM估计的精度都较高.

1 离散型分布左截断右删失数据试验模型

设（X，Y，T）是一离散型随机变量，X的分布函数为F（x，p）＝P（X≤x），分布律为f（x，p）.这里：p是参数；Y是一右删失随机变量，分布函数为G（y），分布律为g（y）；T是一左截断随机变量，分布函数为H（t），分布律为h（t），且Y，T的分布与参数p无关.假定X，Y，T是相互独立取正整数的随机变量，X是我们感兴趣的随机变量.左截断右删失数据的试验模型是：仅在Zi≥Ti时得到观察数据（Zi，Ti，δi），而在Zi＜Ti下无法得到任何观察值，其中：下面求样本的似然函数：

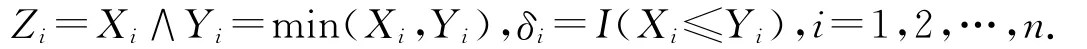
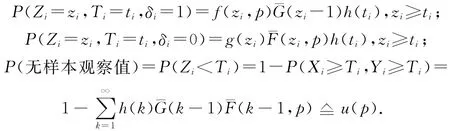
其中

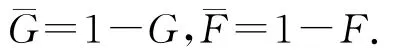
为了叙述与书写方便，我们假定前n1个样本有观察值，剩下的n2个样本没有观察值（n1＋n2＝n）.则基于数据｛（Zi，Ti，δi），1≤i≤n1｝的似然函数为

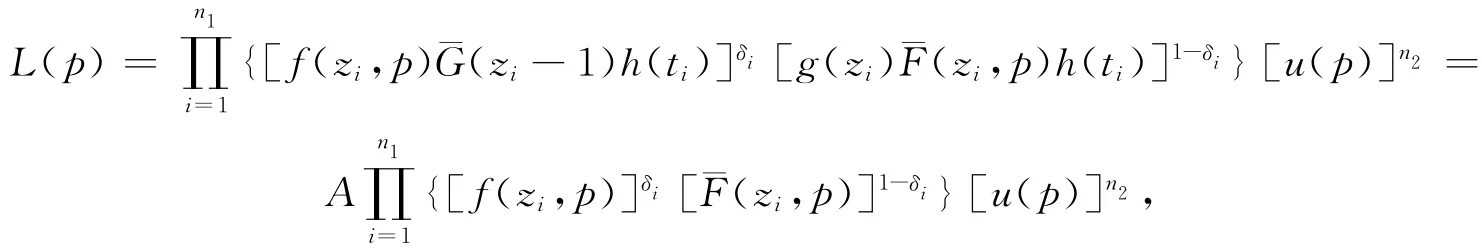
其中

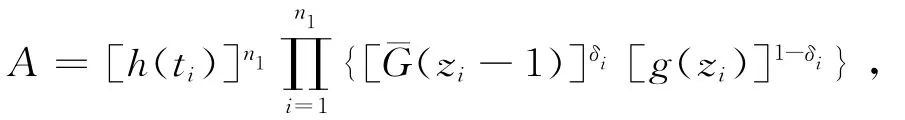
且A与参数p无关.

2 左截断右删失数据下几何分布参数点估计的两种方法

当Xi服从几何分布Geo（p）时，我们介绍参数p点估计的两种方法.

2.1 极大似然估计法

基于数据｛（Zi，Ti，δi），1≤i≤n1｝的似然函数为

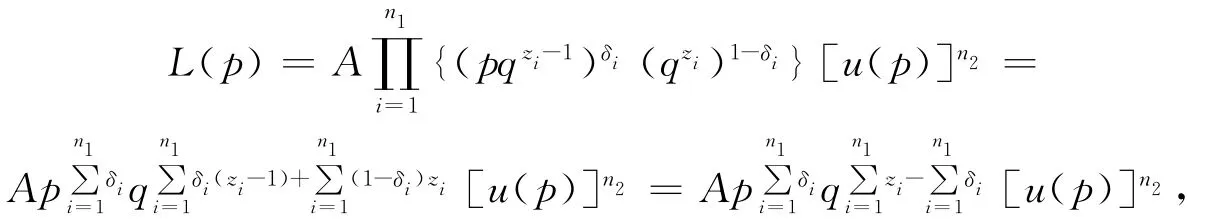
其中

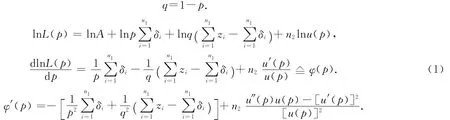
由于

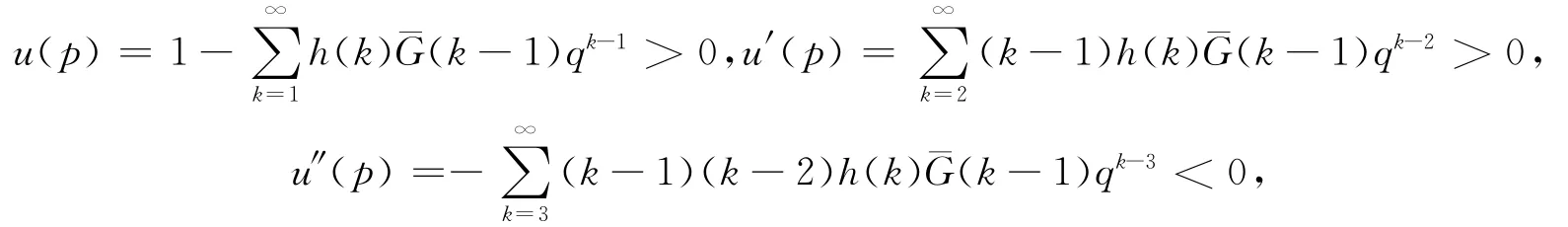
所以φ′（p）＜0.则φ（p）是p的严格减函数，并且

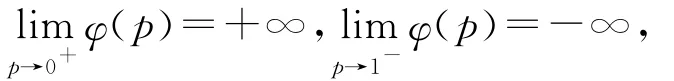
由于u（p）与删失和截断变量的分布有关，从而导致u（p）的表达式一般会很繁琐，所以＾p的显式表达式通常很难得到，这时可以通过数值方法（如二分法）获得，这个＾p就是p的MLE.实际操作中可利用R软件中的uniroot（ ）函数得到＾p.

注1 如果Y服从Geo（p1），T服从Geo（p2），则

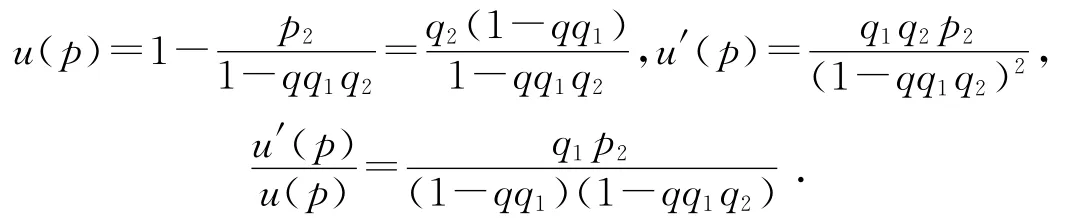
把u（p）和u′（p）带入（1）式，可得到对数似然方程

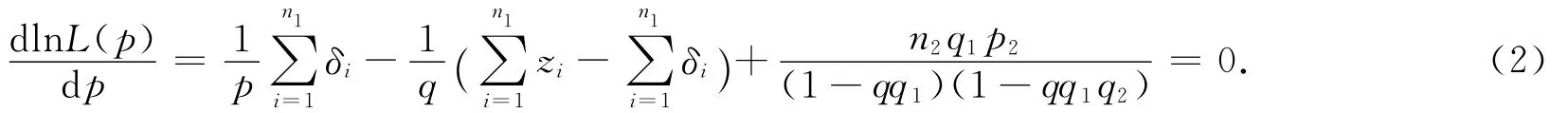
2.2 EM算法

由于左截断右删失数据下几何分布的似然函数比较复杂，下面添加部分缺损的Xi的值以便获得较简单的似然函数.

若第i个样本有观察值且δi＝0，只知道Xi＞zi，虽然Xi的值有缺损，但由于¯F（zi，p）＝qzi比较简单，所以此Xi的值就不添加了.

若第i个样本没有观察值，添加其观察值为（Wi，αi），其中：

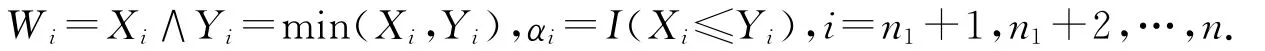
则

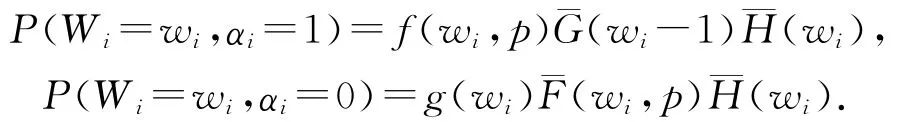
可得似然函数

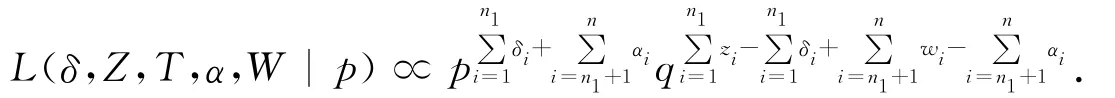
对于p如果没有任何先验信息可利用时，可取π（p）为（0，1）上的均匀分布；对于p如果有先验信息时，可取共轭先验分布贝塔分布Be（b，c），即π（p）∝pb－1qc－1，0＜p＜1，b＞0，c＞0.实际上（0，1）上的均匀分布是Be（1，1）.

下面假设对于p没有任何先验信息可利用，取π（p）为（0，1）上的均匀分布，则p的添加后验分布为

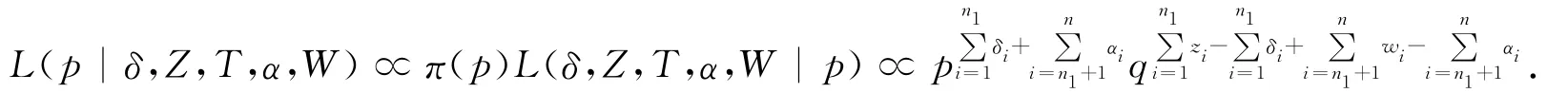
在第m＋1次迭代中，假设有估计值p（m），则可通过E步和M步得到p的一个新的估计.为了书写方便，简记（｜p（m），δ，Z，T）为（｜·）.

E步

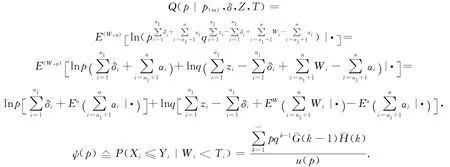
显然，在p（m），δ，Z和T给定下，

故

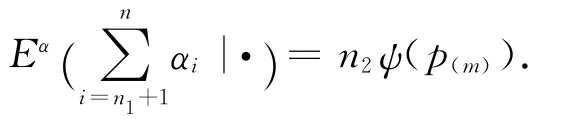
在p（m），δ，Z和T给定下，（Wi，αi）的分布律为：

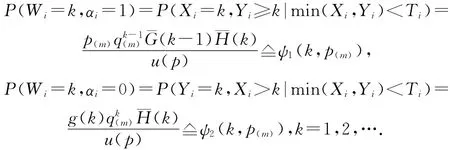
则（Wi，αi）关于Wi的边缘分布律为：

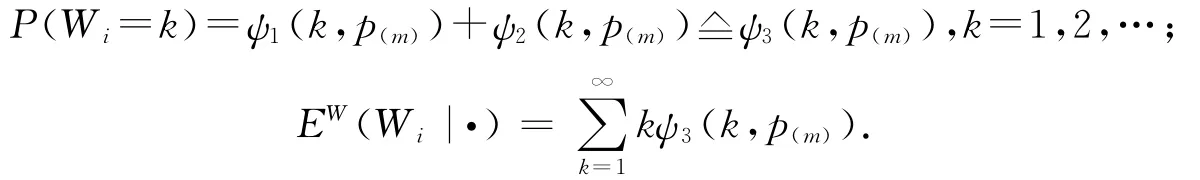
则

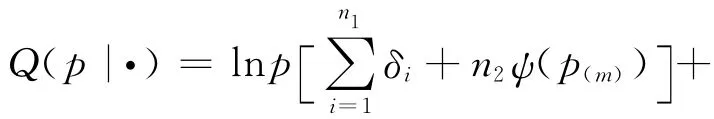
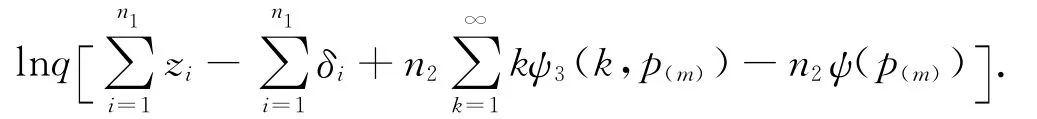
M步

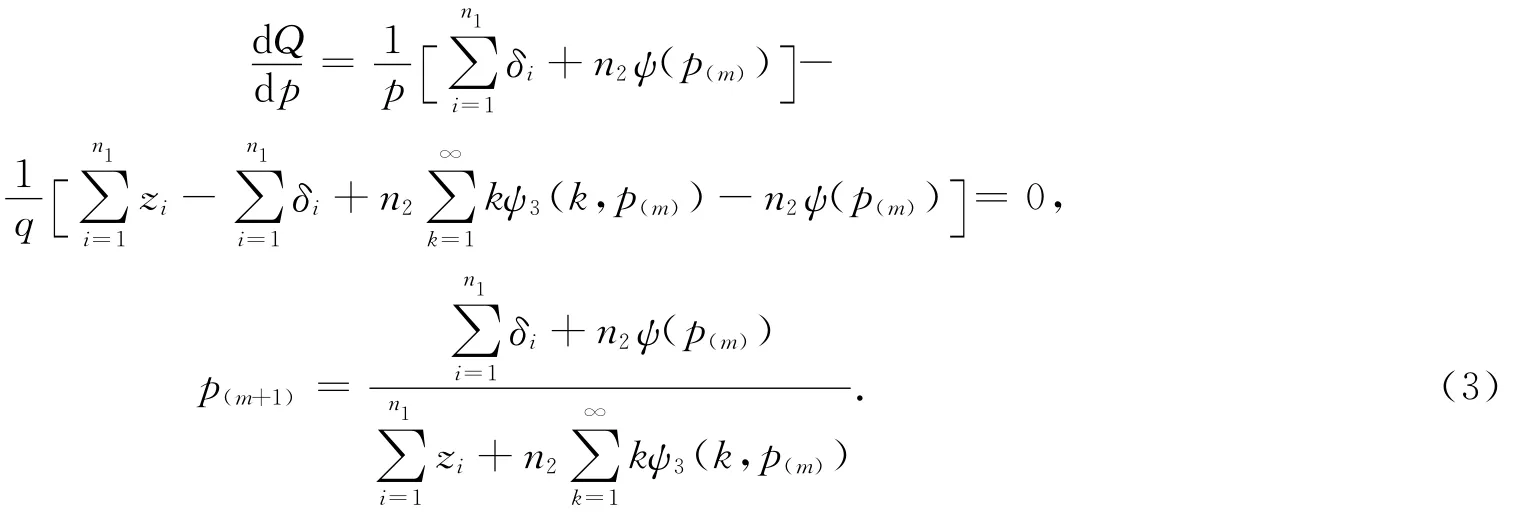
（3）式给出了由EM算法得到的参数p的迭代公式.

注2 由于L（p｜δ，Z，T）＝L（p）≤L（＾p），其中＾p是MLE，所以L（p｜δ，Z，T）是有界函数，由EM算法的性质可知［14］，上述的EM算法是收敛的.

由ψ（p）和ψ3（k，p）的表达式可以看出，选择恰当的右删失变量和左截断变量会使EM迭代公式变得简洁.若Y服从Geo（p1），T服从Geo（p2），下面求具体的迭代公式.

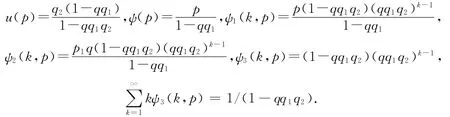
再根据（3）式，可得EM迭代公式

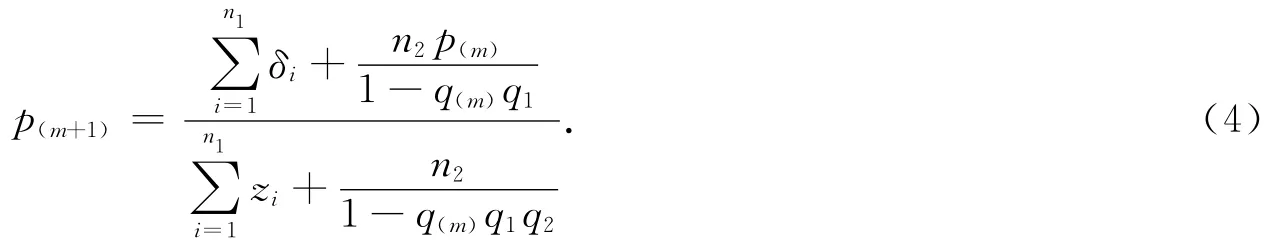
其中：

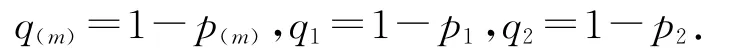
3 随机模拟

基于上面的讨论，下面进行随机模拟试验.

设Xi服从Geo（0.4），Yi服从Geo（0.6），Ti服从Geo（0.9），样本容量分别取n＝30，50，100，200，300，500，800.为了准确性，对每一固定样本容量产生1 000个随机样本，由每个样本计算出一个估计值，然后取这1 000个估计值的算术平均值作为这一样本容量下参数的估计值.运用EM算法时从p（0）＝0.5开始迭代.

随机模拟的主要理论依据是（2）式和（4）式，编写R程序时用到的函数主要有rgeom（ ），min（ ），uniroot（ ）.

随机模拟结果见表1.

表1 左截断右删失数据下几何分布参数估计的随机模拟结果

由表1可以看出，p的MLE和EM估计的差别不大，与真值0.4的偏差都不超过1%；样本容量对估计值的影响也不大.说明得到的估计值是比较稳定的，并且精度也较高.在运用EM算法进行模拟时发现，迭代6次左右即可收敛，收敛速度很快，并且实际操作很方便.相比之下，极大似然法在解对数似然方程时的数值计算速度就显得稍慢些.

［1］ BHOJ，DINESHS，ABSANULLAH M.Estimation of the generalized geometric distribution using ranked set sampling［J］.Biometrics，1996（52）：685－694.

［2］ FERGUSON T S.A characterization of the geometric distribution［J］.Amer Math Mothly，1972，27（2）：256－260.

［3］ 徐晓岭，费鹤良，王蓉华.几何分布的两个统计特征［J］.应用概率统计，2006，22（1）：10－20.

［4］ 魏立力，张文修.几何分布的一类贝叶斯停止判决法则［J］.应用数学学报，2003，26（3）：181－185.

［5］ 刘银萍.截断情形下几何分布的参数估计［J］.东北师大学报：自然科学版，2009，41（3）：14－16.

［6］ 徐晓岭，王蓉华，费鹤良.几何分布产品定数截尾场合下参数的点估计［J］.强度与环境，2009，36（2）：51－63.

［7］ LAI T L，YING Z.Estimating a distribution function with thuncated and censored Data［J］.The Annals of Statistics，1991，19：417－442.

［8］ GU M G，LAI T L.Functional laws of the iterated logarithm for the product－limit estimatorof a distribution function under random censorship or truncated［J］.The Annals of Probability，1990，18：160－189.

［9］ ZHOU YONG，SUN LIU－QUAN.Sequential confidence bands for quantile densities under truncated and censored data［J］.Acta Mathematicae Applicatae Sinica：English Series，2005，21（2）：311－322.

［10］ SUN LIU－QUAN.Fixed design nonparametric regression with truncated and censored Data［J］.Acta Mathematicae Applicatae Sinica：English Series，2003，19（2）：229－238.

［11］ 周勇，吴国富.左删失右截断数据的分位数的固定宽度序贯置信区间估计［J］.应用数学学报，2002，25（2）：204－216.

［12］ 刘焕彬，孙六全.截断与删失数据下的一个回归方法［J］.应用数学学报，2005，28（1）：1－10.

［13］ 苟列红.左截断右删失数据下半参数模型风险率函数估计［J］.应用数学学报，2005，28（4）：675－688.

［14］ MCLACHLAN G，KRISHNAN T.The EM algorithm and extensions［M］.New York：John Wiley ＆Sons，2007：83.

Point estimation of the parameter of geometric distribution for truncated and censored data

HE Chao－bing1，LIU Hua－wen2
（1.School of Mathematics and Statistics，Anyang Normal University，Anyang 455000，China；2.School of Mathematics，Shandong University，Jinan 250100，China）

In this paper，we firstly prove the existence and uniqueness of MLE of the parameter of geometric distribution for truncated and censored data，then give the iterative formula of the parameter by EM algorithm.Finally random simulation tests are conducted，and the results show that the MLE and EM estimation of the paramete are both fairly accurate.

left truncation and right censorship；geometric distribution；maximum likelihood estimation；EM algorithm；random simulation

O 213.2 ［学科代码］ 110·7120

A

（责任编辑：陶 理）

1000－1832（2014）02－0025－05

10.11672／dbsdzk2014－02－006

2013－04－17

国家自然科学基金资助项目（61174099）；河南省教育厅自然科学基金资助项目（2011B110001）.

何朝兵（1975—），男，硕士，讲师，主要从事概率统计研究；刘华文（1964—），女，博士，教授，博士研究生导师，主要从事随机数学研究.