一类三点边值问题正解的存在性和唯一性

苗凤华，宋玥蔷

（1.长春师范大学数学学院，吉林长春130032；2.长春师范大学科研处，吉林长春130032；3.吉林大学符号计算与知识工程教育部重点实验室，吉林长春130012）

一类三点边值问题正解的存在性和唯一性

苗凤华1，宋玥蔷2，3

（1.长春师范大学数学学院，吉林长春130032；2.长春师范大学科研处，吉林长春130032；3.吉林大学符号计算与知识工程教育部重点实验室，吉林长春130012）

研究了一类带有递增同胚和正同态算子的三点边值问题，利用偏序集上的不动点定理证明了该问题正解的存在性和唯一性，并且证明了这个正解是严格单调递增的.

偏序集；不动点定理；正解

本文考虑如下三点边值问题：

其中φ是递增同胚和正同态算子，且φ（0）＝0.

最近，具有递增同胚和正同态算子的多点边值问题正解的存在性和多解性越来越受到广泛关注［13］，在假设非线性项f满足一定的条件下，可以利用锥上的不动点定理证明正解的存在性和多解性.但是对于递增同胚和正同态算子的三点边值问题（1）—（2）正解的唯一性还没有结果.为此，本文受文献［2，4］的启发将利用偏序集上的不动点定理来证明问题（1）—（2）正解的存在性和唯一性，并且证明这个正解是严格单调递增的.

偏序集上的不动点定理以及其应用见文献［4－8］.

1 预备知识

首先我们给出本文所要用的偏序集上的不动点定理.

定理1.1［5］设（E，≤）是一个偏序集，d是E上的一个度量使得（E，d）是一个完备的度量空间.假设E满足下面的条件：

令T：E→E是一个非减映射使得

其中ψ：［0，＋∞）→［0，＋∞）是一个连续非减函数，使得ψ在（0，＋∞）上是正的，ψ（0）＝0，并且.如果存在x0∈E，并且x0≤T（x0），那么T有一个不动点.

如果我们考虑（E，≤）满足条件：

那么我们有下面的结论.

定理1.2［6］设（E，≤）是一个偏序集，d是E上的一个度量，使得（E，d）是一个完备的度量空间.假设E满足条件（3）和（4），则不动点是唯一的.

本文所采用的基本空间是E＝C［0，1］，则E是一个实的Banach空间，其范数为注意到这个空间可以赋予偏序为x，y∈C［0，1］，x≤y⇔x（t）≤y（t），t∈［0，1］.在文献［6］中证明了（C［0，1］，≤）有经典度量满足定理1.1中的条件（3）.更进一步的，对任意的x，y∈C［0，1］，函数max｛x，y｝∈C［0，1］，（C［0，1］，≤）满足条件（4）.

2 主要结果及其证明

定理2.1 假设下面的条件成立：

（Ⅰ）a（t）是一个非负可测函数，并且在区间［0，1］的任何一个子区间上不为零，满足

（Ⅱ）f：［0，＋∞）→［0，＋∞）是连续的，并且关于变量u是非减的；f（u（t））≢0，对任意的t∈Z⊂［0，1］，并且μ（Z）＞0（μ为Lebesgue测度）；

则边值问题（1）—（2）存在唯一且严格单调递增的正解u（t）.

证明 首先考虑锥K＝｛u∈C［0，1］：u（t）≥0｝.则K是C［0，1］中的一个闭子集，赋予距离以后，锥K是一个完备的度量空间.

其次，考虑算子T，定义

由条件（Ⅰ），（Ⅱ）可知T（K）⊂K.

最后，我们来证明满足定理1.1和定理1.2所有的条件.

由条件（Ⅱ）和u≥v可知

这就意味着算子T是非减的.另一方面，由条件（Ⅲ），对任意的u≥v，我们有

因为函数h（x）＝ln（x＋1）是非减的，又由条件（Ⅲ）可知

令ψ（x）＝x－ln（x＋1）.显然ψ：［0，＋∞）→［0，＋∞）是连续的，非减且.则对任意的u≥v有

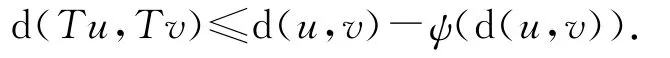
由条件（Ⅰ）和（Ⅱ）我们知道

因此，由定理1.1知，边值问题（1）—（2）至少有一个非负解.又因为（K，≤）满足条件（4），所以，由定理1.2证明边值问题（1）—（2）是唯一的.再由算子T的定义和条件（Ⅰ）—（Ⅱ）易证这个正解是严格递增的.证毕.

［1］ LIANG S H，ZHANG J H.The existence of countably many positive solutions for nonlinear singular m－point boundary value problems［J］.J Comput Appl Math，2008，214：78－89.

［2］ LIU B F，ZHANG J H.The existence of positive solutions for some nonlinear boundary value problems with linear mixed boundary conditions［J］.J Math Anal Appl，2005，309：505－516.

［3］ LIU B F，ZHANG J H.The existence of positive solutions for some nonlinear equation systems［J］.J Math Anal Appl，2006，324：970－981.

［4］ CABALLERO MENA J，HARJANI J，SADARANGANI K.Existence and uniqueness of positive and nondecreasing solutions for a class of singular fractional boundary value problems［J］.Boundary Value Problems，2009：1－10.

［5］ HARJANI J，SADARANGANI K.Fixed point theorems for weakly contractive mappings in partially ordered sets［J］.Nonlinear Anal，2009，71：3403－3410.

［6］ NIETO J J，RODRÍGUEZ－LÓPEZ R.Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations［J］.Order，2005，22：223－239.

［7］ NIETO J J，RODRÍGUEZ－LÓPEZ R.Fixed point theorems in ordered abstract spaces［J］.Proceedings of the American Mathematical Society，2007，135：2505－2517.

［8］ REGAN D，PETRUSEL A.Fixed point theorems for generalized contractions in ordered metric spaces［J］.J Math Anal Appl，2008，341：1241－1252.

Existence and uniqueness of positive solutions to a class of three－point boundary value problem

MIAO Feng－hua1，SONG Yue－qiang2，3
（1.College of Mathematics，Changchun Normal University，Changchun 130032，China；2.Scientific Research Department，Changchun Normal University，Changchun 130032，China；3.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education，Jilin University，Changchun 130012，China）

In this paper，we consider a class of three－point boundary value problem with increasing homeo－morphism and positive homomorphism.By using a fixed－point theorem in partially ordered sets，we obtain the existence and uniqueness of positive and strictly increasing solutions to the above boundary value problem.

partially ordered sets；fixed－point theorem；positive solution

O 175.14 ［学科代码］ 110·44

A

（责任编辑：陶 理）

1000－1832（2014）02－0009－03

10.11672／dbsdzk2014－02－002

2013－05－13

吉林省自然科学青年基金资助项目（20130522100JH）；吉林省教育厅“十二五”科学技术研究项目（吉教科合字2013第252号）；教育部重点实验室开放课题项目（93K172013K03）；长春师范学院自然科学基金资助项目（2011第02号）.

苗凤华（1968—），女，硕士研究生，副教授，主要从事非线性微分方程理论及应用研究.