峰值折射率对正弦型函数光子晶体缺陷模的影响

熊翠秀，邓杨保，邓曙光，王景艳

（1.湖南城市学院通信与电子工程学院，益阳413000；2.保山学院数学学院，保山678000）

峰值折射率对正弦型函数光子晶体缺陷模的影响

熊翠秀1，邓杨保1，邓曙光1，王景艳2

（1.湖南城市学院通信与电子工程学院，益阳413000；2.保山学院数学学院，保山678000）

为了分析峰值折射率对1维正弦型函数光子晶体缺陷模的影响，首先对折射率按正弦规律变化的介质进行离散化，然后应用传输矩阵法计算了1维光子晶体（AB）mC（BA）m的透射谱，分析了各介质层的折射率峰值对该结构1维正弦型函数光子晶体缺陷模的影响。结果表明，随着峰值折射率的增大，缺陷模红移，且频率越高缺陷模红移现象越明显；低折射率介质的峰值折射率对缺陷模频移的影响比较显著。这一结果对光子晶体的设计有一定的参考价值。

光电子学；缺陷模红移；介质离散化；传输矩阵法

引 言

由于光谱的特殊性，自从1987年JOHN［1］和YABLONOVITCH［2］提出了光子晶体的概念，光子晶体就得到了人们的关注和应用。

随着信息技术的发展，对器件的性能提出了更多的要求，于是陆续提出了不同结构的非常规光子晶体，如含有折射率与频率有关的色散材料及特异材料的光子晶体［3-5］、含有折射率受外加电压及外磁场调控的液晶光子晶体［6-7］、含有相对介电常数受温度和外磁场调控的超导光子晶体［8-9］和折射率与空间坐标有关的函数型光子晶体［10-16］等。参考文献［11］～参考文献［12］中用函数型光子晶体中的传输矩阵法主要研究了函数光子晶体的带隙结构及各结构参量对带隙结构的影响，参考文献［13］～参考文献［16］中用同样的方法研究了1维函数型光子晶体的缺陷模，其中参考文献［13］中的研究对象是折射率为向上的折线型函数光子晶体中引入常规介质缺陷层，详细分析了缺陷的折射率、厚度及位置对该结构缺陷模的影响，参考文献［14］～参考文献［15］中的研究对象是1维线性函数光子晶体中引入常规介质缺陷层，其中参考文献［14］中分析了缺陷层的位置和折射率对缺陷模的影响，而参考文献［15］中着重研究了周期数和缺陷层的位置、折射率及光学厚度对缺陷模的影响，而参考文献［16］中研究了1维正弦型函数光子晶体中的缺陷模，在研究过程中折射率的系数取一定值（即峰值折射率一定），分析了缺陷层的个数对缺陷模的影响，其次，用缺陷层的消光系数来降低或消除缺陷模对透射率的影响。参考文献［13］～参考文献［16］中的研究表明，缺陷的各个参量对各种形式的1维函数型光子晶体的缺陷模及电场分布都有影响，但都没有涉及到非缺陷层的参量对缺陷模的影响。为了探讨正弦函数的折射率系数对1维正弦型函数光子晶体缺陷模的影响，作者先把正弦型函数折射率介质层离散化［17］，用平均折射率等效为每一小层的折射率，再用传输矩阵法［18］计算正弦型函数光子晶体的透射率，分析各个系数对缺陷模的影响。结果表明，各个系数对缺陷模的影响程度有所不同。这为光子晶体的设计提供一定的理论依据。

1 理论模型与计算方法

1维光子晶体（AB）mC（BA）m的结构如图1所示，其中m表示周期数。令光波沿着z方向传播，图中A和B两种介质是折射率与空间坐标z有关的正弦型函数介质，而缺陷层C是常规介质。A是高折射率介质，而B是低折射率介质，A介质和B介质的折射率分别由下面两个式子表示：

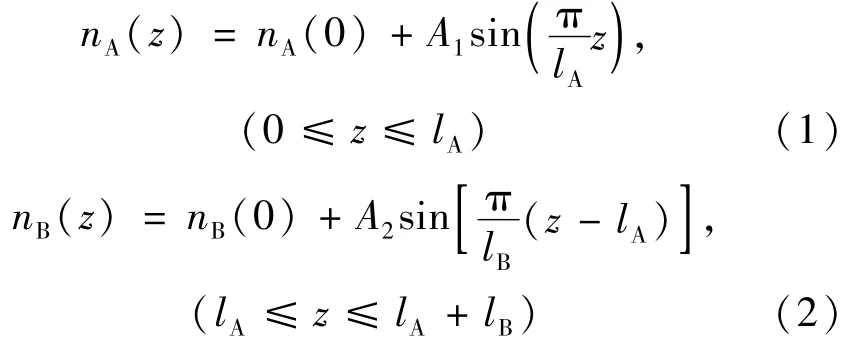
式中，lA和lB分别是A和B介质的几何厚度，nA（0）和nB（0）分别是A和B介质起始端的折射率，A1和A2分别是A介质和B介质的折射率系数。

计算过程中，对于常规介质层，直接采用传输矩阵［18］表示光波在介质中的传输特性；而对于折射率随空间坐标z按正弦函数规律变化的介质层，先把介质离散化［17］，即把每半个周期分成j小层，每小层的几何厚度为（或），用每一小层的平均折射率等效为该小层的折射率，离散化后，每小层的光学传输特性用传输矩阵表示，故用传输矩阵法［18］计算透射率。

2 数值计算结果与分析

参量选取参照参考文献［16］，即高折射率介质A、低折射率介质B起始端的折射率统一取nA（0）＝3.37和nB（0）＝1.544，缺陷C的折射率统一取nC＝4.8，周期数统一取m＝5。假设所有介质都是非铁磁性材料。在MATLAB 7.0环境下编程计算透射率，计算过程中角频率ω对中心角频率ω0归一化，表示为

2.1 高折射率介质为正弦型函数介质

考虑高折射率介质A的折射率随空间坐标z按正弦函数规律变化，介质B和介质C为常规介质，即A2＝0。取B介质和C介质的光学厚度都为而对折射率按正弦函数规律变化的高折射率介质A，令（λ为中心波长），且在参量A变01化时，A介质的几何厚度始终保持不变；每个A层离散化为20层（即j＝20）。令光波垂直入射，则TE和TM波的透射谱一样。图2中给出了折射率系数A1分别取0，0.1，0.2，0.3，0.4，0.5，0.6和0.7时的透射谱。当A1＝0时，nA（z）≡nA（0），表示高折射率介质A也为常规介质。图2a和图2b分别对应于所取参量下第一禁带和第二禁带的透射率与归一化角频率的关系。由图2可知，在所取参量下，所有介质都为常规折射率介质（即图中A1＝0的情况）时，第一、二禁带分别出现了1个透射峰，即为缺陷模，缺陷模分别位于ω／ω0＝0.5和ω／ω0＝1.5的地方。由图2可知，随着高折射率介质的折射率系数A1的增大，这两个禁带的中心都发生红移，缺陷模也发生红移，但是缺陷模的红移速率慢于禁带的红移速率，故当A1增大到较大时，缺陷模会消失；比较图2a和2b可以发现，第一禁带内的缺陷模红移的速率慢于第二禁带内缺陷模的红移速率，但是由于第二禁带红移速度比较快，因此第二禁带内的缺陷模消失得比较早。

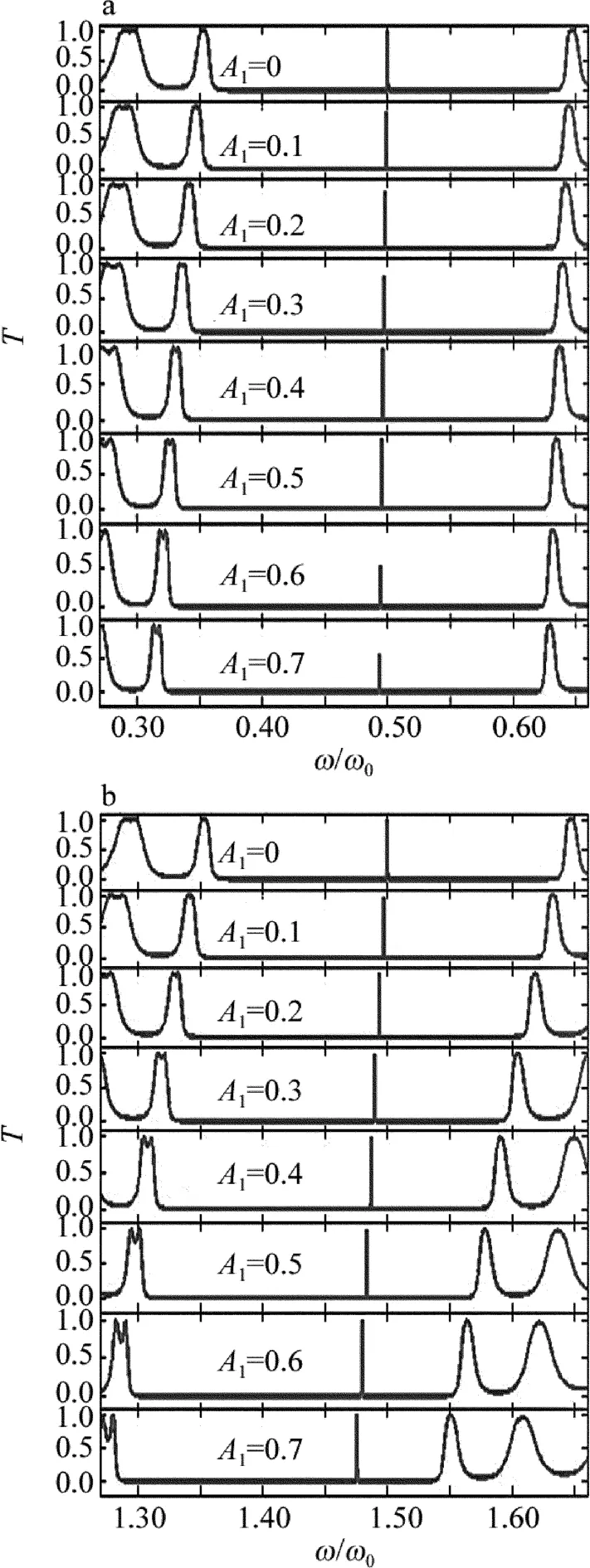
Fig.2 Transmission spectrum of 1-D sine function photonic crystals when A is sine function medium

2.2 低折射率介质为正弦型函数介质

考虑低折射率介质B的折射率随空间坐标z按正弦函数规律变化，介质A和介质C为常规介质，即A1＝0。取介质A和介质C的光学厚度都为λ0／2，而对折射率按正弦函数规律变化的低折射率介质B，令nB（0）lB＝λ0／2（λ0为中心波长），且在参量A2变化时，B介质的几何厚度始终保持不变；每个B层离散化为20层（即j＝20）。令光波垂直入射。图3中给出了折射率系数A2分别取0，0.1，0.2，0.3，0.4，0.5，0.6和0.7时的透射谱。当A2＝0时，nB（z）≡nB（0），表示低折射率介质B也为常规介质。图3a和图3b中分别对应于所取参量下第一禁带和第二禁带的透射率与归一化角频率的关系。由图3可知，在所取参量下，所有介质都为常规折射率介质（即图中A2＝0的情况）时，第一、二禁带分别出现了一个透射峰，即为缺陷模，缺陷模分别位于ω／ω0＝0.5和ω／ω0＝1.5的地方，随着低折射率介质的折射率系数A2增大，禁带及缺陷模都发生红移，且A2进一步增大会导致缺陷模消失，这些现象与图2类似。

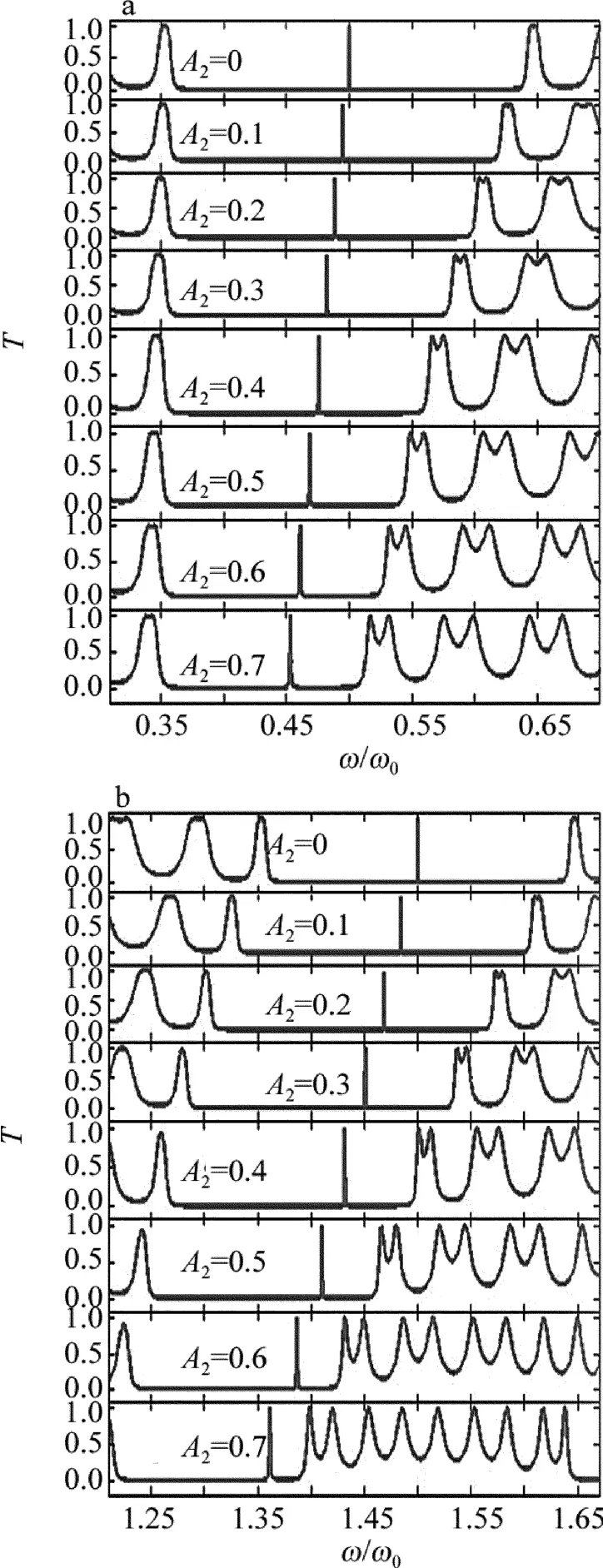
Fig.3 Transmission spectrum of 1-D sine function photonic crystals when B is sine function medium

2.3 综合比较

在本文中所取的函数形式下，高折射率介质A和低折射率介质B的峰值折射率分别为nA（0）＋A1和nB（0）＋A2，折射率系数A1或A2增大意味着峰值折射率增大。由图2和图3可知，对于1维正弦型函数光子晶体，无论是高折射率介质A还是低折射率介质B的折射率系数增大，也即峰值折射率增大，禁带内的缺陷模都会发生红移。但相同参量下不同禁带内的缺陷模红移量有所不同，同一禁带内的缺陷模在不同参量下的红移量也不同。

令光波垂直入射。为了比较高、低折射率介质A和B的峰值折射率对不同禁带内缺陷模频移的影响，把折射率按正弦规律变化的介质进行离散化，再用传输矩阵法计算不同折射率系数下的透射率，得到不同禁带内缺陷模的归一化角频率与折射率系数A1或A2的关系如图4所示。具体计算中所取的两种参量见下。

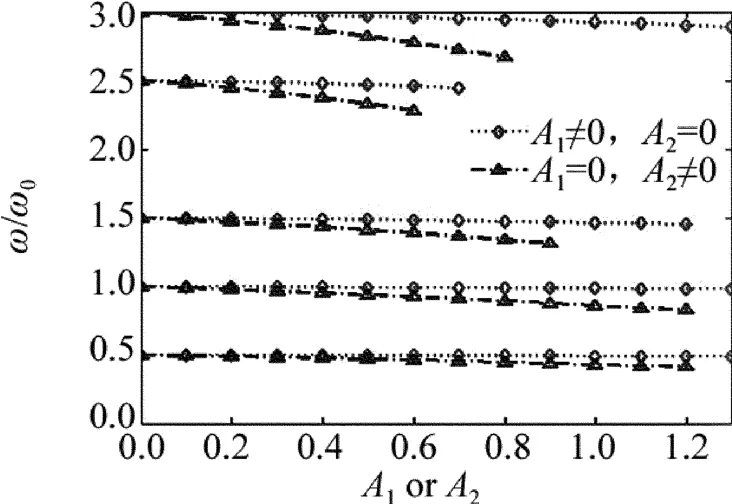
Fig.4 Comparison of the frequency of defect modes with different coefficients of refractive indexes A1（or A2）

第1组：nA（0）lA＝nB（0）lB＝nClC＝λ0／2（lC是缺陷C的几何厚度），对应常规1维光子晶体，这时归一化角频率凡是满足ω／ω0＝0.5（2k＋1）（k＝0，1，2，…）的附近都有以该归一化角频率为中心的禁带，禁带的中心频率处都有一透射峰，即缺陷模；分别令高、低折射率介质为正弦型函数介质，保持几何厚度不变，逐渐增大相应的折射率系数A1或A2，分别得到每个禁带内缺陷模的归一化角频率，计算中取j＝20。

第2组：nA（0）lA＝nB（0）lB＝nClC＝λ0／4，对应常规1维光子晶体，这时归一化角频率凡是能够满足ω／ω0＝2k＋1（k＝0，1，2，3，…）的附近都有以该归一化角频率为中心的禁带，禁带的中心频率处都有一透射峰，即缺陷模；也分别令高、低折射率介质为正弦型函数介质，保持几何厚度不变，逐渐增大相应的折射率系数A1或A2，分别得到每个禁带内缺陷模的归一化角频率，取j＝20。图4中，“◇”形曲线都对应于高折射率介质A为正弦型函数介质的情况，而“△”形曲线都对应于低折射率介质B为正弦型函数介质的情况。图4的每个禁带内的两条曲线中，“◇”形曲线始终比“△”形曲线平坦，即同一个禁带内的缺陷模，低折射率介质B的峰值折射率对缺陷模的频移影响更显著；同一组线型曲线中，归一化角频率越大，缺陷模的频移曲线越陡，也就是说峰值折射率对不同频率处缺陷模的影响程度不一致，频率越高，峰值折射率的影响越显著。

值得注意的是，图4中不同曲线的数据数不相同，这是因为随着折射率系数的增大，禁带和缺陷模都发生红移，而禁带频移速率比缺陷模快，导致缺陷模消失，由于不同禁带内缺陷模红移的程度不一致，有的禁带内的缺陷模消失得早，故能取的数据个数不一致；另外，随着折射率系数的增大，会出现新的禁带，新增的禁带内的缺陷模也会随折射率系数的增大而发生红移。

3 结 论

研究了含常规折射率介质缺陷1维正弦型函数光子晶体的缺陷模频移特性。高折射率介质A和低折射率介质B的正弦函数的折射率系数A1和A2都对缺陷模的位置有影响；随着系数的增大，即折射率的峰值增大，缺陷模发生红移，且频率越高，缺陷模红移现象越显著；高、低折射率介质中，低折射率介质B的峰值折射率使缺陷模红移的效果更显著。

［1］ JOHN S.Strong localities of photons in certain disordered dielectric super lattices［J］.Physical Review Letters，1987，58（23）：2486-2489.

［2］ YABLONOVITCH E.Inhibited spontaneous emission in solid-state physics and electronics［J］.Physical Review Letters，1987，58（20）：2059-2062.

［3］ KOCAMAN S，ARAS M S，HSIEH P，et al.Zero phase delay in negative-refractive-index photonic crystal superlattices［J］.Nature Photonics，2011，5（8）：499-505.

［4］ WU J J.Effect of material dispersion on bandgap of one-dimensional graded photonic crystals［J］.Journal of Synthetic Crystals，2011，40（2）：474-479（in Chinese）.

［5］ YUAN Q H，XIE K，HAN Y F.Study on 1-D photonic crystal containing negative refraction material with impurity defects［J］.Laser Technology，2010，34（2）：232-235（in Chinese）.

［6］ WU C Y，ZOU Y H，TIMOFEEV I，et al.Tunable bi-functional photonic device based on one-dimensional photonic crystal infiltrated with a bistable liquid-crystal layer［J］.Optics Express，2011，19（8）：7349-7355.

［7］ ARKHIPKIN V G，GUNYAKOV V A，MYSLIVETS S A，et al.Electro-and magneto-optical switching of defect modes in one-dimensional photonic crystals［J］.Journal of Experimental and The-oretical Physics，2011，112（4）：577-587.

［8］ THAPA K B，SRIVASTAVA S，TIWARI S.Enlarged photonic band gap in heterostructure of metallic photonic and superconducting photonic crystals［J］.Journal of Superconductivity and Novel Magnetism，2010，23（4）：517-525.

［9］ WU J J，GAO JX.Extraordinary optical properties of fibonacci quasi-peri-odic 1-D superconducting photonic crystals in near-zeropermittivity operation range［J］.Optoelectronics Letters，2013，9（4）：289-292.

［10］ CHENG Y.Band gap of biperiodic photonic crystals［J］.Laser Technology，2011，35（4）：570-572（in Chinese）.

［11］ WANG G H，WANG Q C，WU X Y，et al.Research on one-dimensional function photonic crystals［J］.Acta Physica Sinica，2012，61（13）：134208（in Chinese）.

［12］ WU X Y，ZHANG B J，YANG JH，et al.Function photonic crystals［J］.Physica，2011，E43（9）：1694-1700.

［13］ WANG Q C.Study band-gap theory of one-dimensional function photonic crystal［D］.Siping：Jilin Normal University，2012：44-55（in Chinese）.

［14］ LIH，ZHANG SQ，WU X Y，et al.Transmission properties of one-dimensional linear function photonic crystal with defect［J］.Journal of Jishou University，2013，34（5）：53-56（in Chinese）.

［15］ WU X Y，ZHANG SQ，ZHANG B J，etal.The effect of defect layer on transmissivity and light field distribution in general function photonic crystals［J］.Physica，2013，E53：1-6.

［16］ BA N，WU X Y，WANG J，et al.Light transmission properties of one-dimensional function photonic crystals［J］.Chinese Journal of Lasers，2012，39（6）：0606001（in Chinese）.

［17］ LIU Q N.Polarization properties of the electromagnetic wave in photonic crystal with sinusoidal refractive index［J］.Chinese Journal of Quantum Electronics，2008，25（2）：198-202（in Chinese）.

［18］ BORN M，WOLF E.Principles of optics［M］.7th ed.Beijing：Publishing House of Electronics Industry，2009：59-61（in Chinese）.

Effect of peak refractive index on defect modes of sine function photonic crystals

XIONG Cuixiu1，DENG Yangbao1，DENG Shuguang1，WANG Jingyan2
（1.College of Communication and Electronic Engineering，Hunan City University，Yiyang 413000，China；2.School of Mathematicas，Baoshan College，Baoshan 678000，China）

In order to investigate effect of the peak refractive index on the defect modes of1-D sine function photonic crystals，the sine function medium was discretized at first，then the transmission spectrum of the 1-D sine function photonic crystal（AB）mC（BA）mwas computed by applying the method of optical transmission matrix，and the effect of peak refractive index of sine function medium on defect modes was analyzed.The results show that the defect modes are redshifted with the increasing of peak refractive index，and the higher the frequency is，the more obvious the red-shift of defect modes is.The obvious effect of frequency shift of defect modes results from the increasing of the peak refractive index of low refractive index medium.The results have a certain reference value for the design of photonic crystal.

optoelectronics；defect mode red-shift；discretization of medium；transfer matrix method

O474

A

10.7510／jgjs.issn.1001-3806.2014.06.020

1001-3806（2014）06-0817-05

湖南省自然科学基金资助项目（14JJ6043）；湖南省益阳市科技计划资助项目（2012JZ09）

熊翠秀（1980-），女，讲师，硕士，现主要从事光学方面的研究。

E-mail：xiongcuixiu＠163.com

2014-01-02；

2014-01-15